可持久化数据结构
所谓可持久化,就是可以保留每一个历史版本,并且支持操作的不可变特性。例如对于线段树而言,可持久化意味着它可以保留多个历史版本的线段树,并且支持对历史版本的访问与修改。
本文将介绍几种常见数据结构的可持久化方式。
1 可持久化线段树
1.1 基本思想
理论上讲主席树指的是可持久化权值线段树,但有时也会用来代指可持久化线段树,毕竟二者没啥差别。
保存每一个历史版本的线段树本身是简单的,直接开一堆线段树就行,但是显然这样做空间会爆炸。
我们考虑当我们进行一次单点修改的时候,实际上只有原树上的一条链被修改了权值。换句话说,当我们新建一个版本的时候,只需要新建一条链的信息,剩下的采用原版本信息即可。这样我们每次新增的节点就达到了 \(O(\log n)\) 个,可以接受。
例如下图即为修改 \(1\) 时新建节点情况:
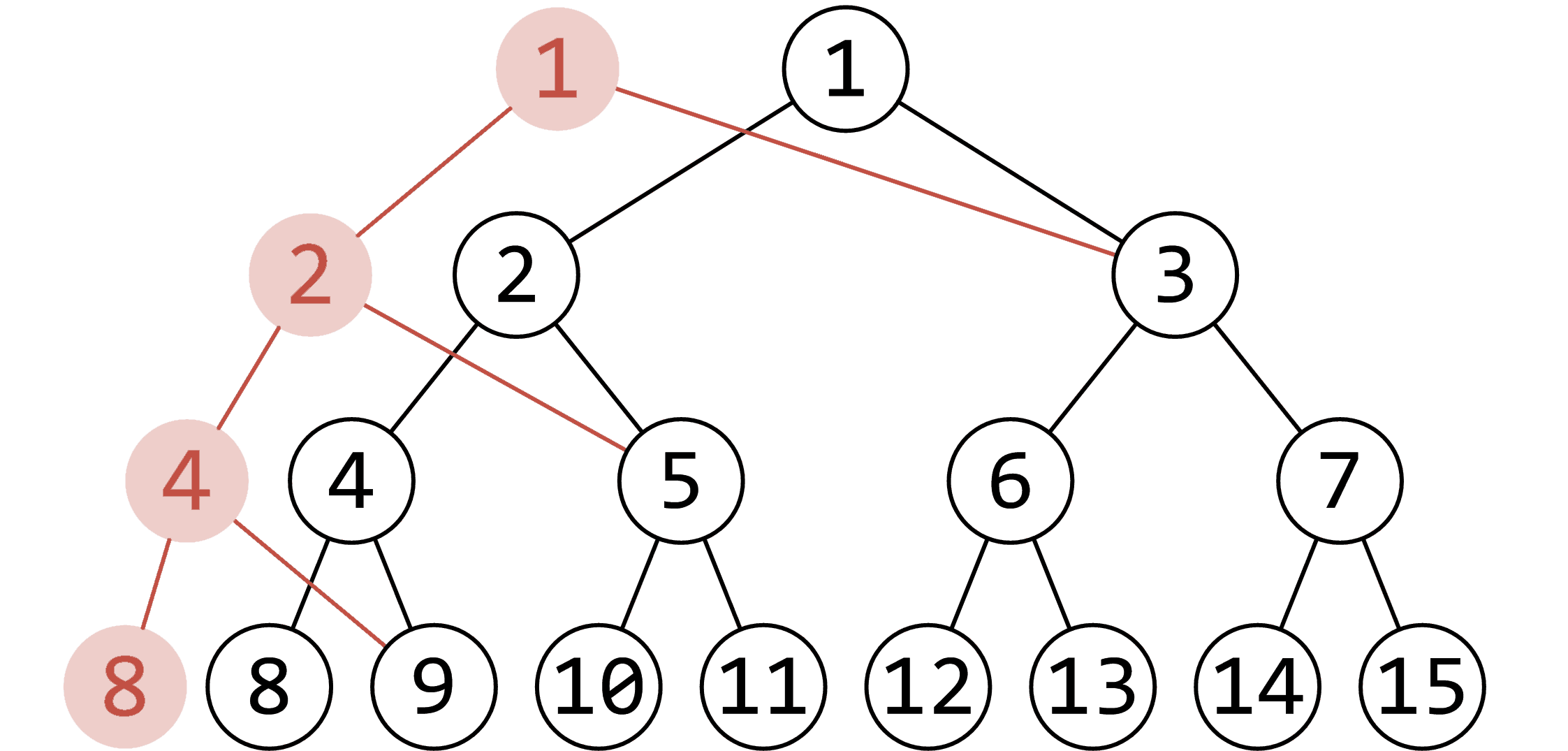
自然,由于每一次会复用原来的节点,所以左右儿子不能用朴素的 \(2\times p,2\times p+1\) 来存储,需要采用类似动态开点的方式存储。
上面我们讲的是单点修改的可持久化线段树,那么区间修改应该如何做呢?
考虑普通线段树怎样进行区间修改,不难想到就是下放标记、上传合并。但是由于可持久化线段树上有复用的节点,所以无法下放懒标记,也无法上传合并信息。这个时候我们想到了标记永久化,通过标记永久化我们就可以不用下放和上传操作,并且仍然只需要修改 \(O(\log n)\) 个节点的信息。如此便可在正确的时空复杂度内完成可持久化线段树的区间修改。
这种复用节点的思想在可持久化数据结构中应用相当广泛,下文依然会有所提及。
1.2 例题
前五例主要运用的是主席树,后面运用的是普通的可持久化线段树。
例 1 【模板】可持久化线段树 2
题意: 求静态区间第 \(k\) 小。
先考虑对于全局求第 \(k\) 小怎么做,这个用权值线段树是显然的。先对原数组离散化,然后建一颗权值线段树。我们在线段树上遍历,如果左子树的数字总个数小于 \(k\),则说明目标在右子树内,遍历右子树即可;否则去遍历左子树。
现在如果要求区间 \([l,r]\) 的第 \(k\) 小值,实际上只需要知道 \([l,r]\) 这段区间内所有数字构成的权值线段树上的信息即可。考虑运用前缀和的思想,我们单次插入数组中的一个元素,建立一颗主席树,则主席树上每一个节点存储的就是 \([1,r]\) 内所有数字的信息。如果要求 \([l,r]\) 内的信息,用 \([1,r]\) 内的信息减去 \([1,l-1]\) 内的信息即可。
代码如下:
#include <bits/stdc++.h>
using namespace std;
const int Maxn = 2e5 + 5;
const int Inf = 2e9;
int n, m, a[Maxn], t[Maxn], tot;
int rt[Maxn];
namespace Sgt {
struct node {
int l, r, sum;
}t[Maxn << 5];
#define lp t[p].l
#define rp t[p].r
int tot = 0;
void build(int &p, int l, int r) {
p = ++tot;
t[p].sum = 0;
if(l == r) return ;
int mid = (l + r) >> 1;
build(lp, l, mid), build(rp, mid + 1, r);
}
int mdf(int p, int l, int r, int x) {//p 为上一版本树上节点
int rt = ++tot;//建新节点
t[rt] = t[p];
t[rt].sum++;
if(l == r) return rt;
int mid = (l + r) >> 1;
if(x <= mid) t[rt].l = mdf(lp, l, mid, x);
else t[rt].r = mdf(rp, mid + 1, r, x);
return rt;
}
int query(int p, int q, int l, int r, int k) {
if(l == r) return l;
int mid = (l + r) >> 1, res = t[t[q].l].sum - t[t[p].l].sum;//前缀和相减
if(res < k) return query(t[p].r, t[q].r, mid + 1, r, k - res);
else return query(t[p].l, t[q].l, l, mid, k);
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; i++) {
cin >> a[i];
t[++tot] = a[i];
}
sort(t + 1, t + tot + 1);
tot = unique(t + 1, t + tot + 1) - t - 1;
for(int i = 1; i <= n; i++) {
a[i] = lower_bound(t + 1, t + tot + 1, a[i]) - t;
}
Sgt::build(rt[0], 1, tot);
for(int i = 1; i <= n; i++) {
rt[i] = Sgt::mdf(rt[i - 1], 1, tot, a[i]);
}
while(m--) {
int l, r, k;
cin >> l >> r >> k;
int pos = Sgt::query(rt[l - 1], rt[r], 1, tot, k);
cout << t[pos] << '\n';
}
return 0;
}
例 2 [SDOI2013] 森林
题意: 维护一个森林,支持合并两个连通块、求两点间权值第 \(k\) 小。
看到维护第 \(k\) 小不难想到主席树,但是这是一个树上问题,那么自然的将序列前缀和转化为树上前缀和即可。因此在主席树上跑的时候,当前权值区间的信息应该是用 \(u\) 处的信息加上 \(v\) 处的信息,减去 \(\text{lca}\) 和 \(\text{lca}\) 的父亲处的信息。
现在的问题就是怎样合并连通块,由于强制在线,除了暴力合并我们似乎没有什么更好的方式。那么就考虑启发式合并,每一次将节点数量小的合并到大的上面,然后暴力重构小的连通块中每一个点在主席树上的信息即可。这样做的复杂度是 \(O(n\log ^2 n)\) 的,完全可以通过。
当然由于我们还需要在合并后求 \(\text{lca}\),所以树剖肯定不可行,只能使用倍增,在暴力重构的时候一起更新倍增数组即可。
例 3 [AHOI2017 / HNOI2017] 影魔
首先考虑这个贡献的含义:假设区间 \((l,r)\) 的最大值是 \(c\),当 \(c<k_l\) 且 \(c<k_r\) 时产生 \(p_1\) 贡献;否则当 \(c<k_l\) 或 \(c<k_r\) 时产生 \(p_2\) 贡献。
那么这就说明要产生贡献肯定有一个端点是最大值,那么考虑枚举 \(c\) 所在位置 \(i\),并预处理出 \(i\) 左侧和右侧第一个大于 \(c\) 的数的位置,记作 \(L_i,R_i\)。此时根据上面所述的贡献,会发现贡献分为如下类型:
- 当 \(L_i\) 在 \([a,b]\) 中时,所有 \(x\in(i,\min(R_i,b + 1))\) 的 \(x\) 可以与 \(L_i\) 一起产生 \(p_2\) 贡献。
- 当 \(R_i\) 在 \([a,b]\) 中时,所有 \(x\in(\max(a-1,L_i),i)\) 的 \(x\) 可以与 \(R_i\) 一起产生 \(p_2\) 贡献。
- 当 \(L_i,R_i\) 均在 \([a,b]\) 中时,\(L_i,R_i\) 可以一起产生 \(p_1\) 贡献。
- 对于任意 \((i,i+1)\) 点对,它们可以一起产生 \(p_1\) 贡献。
我们以第一个举例说明如何维护。当我们遇到一个 \(L_i\) 时,将 \((i,R_i)\) 这个区间中的数全部 \(+p_2\) 的贡献,然后对于一组询问 \([a,b]\),我们直接查询 \([a,b]\) 中所有数的和即可满足 \(x\in(i,\min(R_i,b + 1))\) 这个要求。但是此时还没有满足 \(L_i\in[a,b]\) 这个要求,不难发现运用一次前缀和之后用在 \(b\) 处求得的答案减去在 \(a-1\) 处求得的答案即可满足该条件,所以利用主席树维护上述信息即可。剩余三个操作是同理的。
代码如下:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int Maxn = 2e5 + 5;
const int Maxm = 1.6e7 + 5;
const int Inf = 2e9;
int n, m, p1, p2;
int a[Maxn];
int pre[Maxn], nxt[Maxn], s[Maxn], top;
int rt[Maxn];
namespace Sgt {
struct node {
int l, r;
ll sum, tag;
}t[Maxm];
#define lp t[p].l
#define rp t[p].r
int tot = 0;
void build(int &p, int l, int r) {
p = ++tot;
if(l == r) return ;
int mid = (l + r) >> 1;
build(lp, l, mid), build(rp, mid + 1, r);
}
int mdf(int p, int l, int r, int pl, int pr, int v) {//区间修改
int rt = ++tot;
t[rt] = t[p];
t[rt].sum += 1ll * (min(pr, r) - max(pl, l) + 1) * v;//直接修改区间和
if(pl <= l && r <= pr) {
t[rt].tag += v;//打标记
return rt;
}
int mid = (l + r) >> 1;
if(pl <= mid) t[rt].l = mdf(lp, l, mid, pl, pr, v);
if(pr > mid) t[rt].r = mdf(rp, mid + 1, r, pl, pr, v);
return rt;
}
ll query(int p, int l, int r, int pl, int pr, ll tag/*当前增加的标记*/) {//区间查询
if(pl <= l && r <= pr) {
return t[p].sum + 1ll * (r - l + 1) * tag;//加上一路上走过来的标记
}
int mid = (l + r) >> 1;
ll res = 0;
if(pl <= mid) res += query(lp, l, mid, pl, pr, tag + t[p].tag);
if(pr > mid) res += query(rp, mid + 1, r, pl, pr, tag + t[p].tag);
return res;
}
}
struct node {
int l, r, v;
};
vector <node> V[Maxn];
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m >> p1 >> p2;
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i <= n; i++) {
while(top && a[s[top]] <= a[i]) top--;
if(top) pre[i] = s[top];
else pre[i] = 0;
s[++top] = i;
}
top = 0;
for(int i = n; i >= 1; i--) {
while(top && a[s[top]] <= a[i]) top--;
if(top) nxt[i] = s[top];
else nxt[i] = n + 1;
s[++top] = i;
}
for(int i = 1; i <= n; i++) {
V[pre[i]].push_back((node){i + 1, nxt[i] - 1, p2});
V[nxt[i]].push_back((node){pre[i] + 1, i - 1, p2});
V[pre[i]].push_back((node){nxt[i], nxt[i], p1});
V[i].push_back((node){i + 1, i + 1, p1});
}
Sgt::build(rt[0], 0, n + 1);
for(int i = 1; i <= n; i++) {
bool flg = 0;
for(auto p : V[i]) {
if(!flg) {
rt[i] = Sgt::mdf(rt[i - 1], 0, n + 1, p.l, p.r, p.v);
flg = 1;
}
else {
rt[i] = Sgt::mdf(rt[i], 0, n + 1, p.l, p.r, p.v);
}
}
}
while(m--) {
int l, r;
cin >> l >> r;
cout << Sgt::query(rt[r], 0, n + 1, l, r, 0) - Sgt::query(rt[l - 1], 0, n + 1, l, r, 0) << '\n';
}
return 0;
}
例 4 [国家集训队] middle
题意: 求出 \(l\in [a,b],r\in [c,d]\) 的所有区间 \([l,r]\) 的中位数的最大值。强制在线。
考虑区间中位数的求法,在此题中最合适且最常见的套路就是二分答案。我们二分中位数 \(mid\),然后看怎样判断其与答案的大小关系。不难想到的是,此时如果 \(\ge mid\) 的数的数量不比 \(<mid\) 的数的数量少,那么 \(mid\) 应该是小于等于最后答案的,否则应该大于最后答案。
将上述条件转化如下:将当前数列中所有 \(\ge mid\) 的数改为 \(-1\),\(< mid\) 的数改为 \(1\),若当前区间的和 \(\le 0\),则说明 \(mid\) 小于等于最终答案。
回到原题,我们二分出 \(mid\) 之后,自然是希望 \(mid\) 比最终答案小,也就是说我们要尽可能找到一个合法区间 \([l,r]\),使它的权值和 \(\le 0\),也就是要让它的和尽可能小。考虑到最后选出的 \([l,r]\) 实际上是从区间 \([a,d]\) 中,删去一个 \([a,b]\) 的前缀与 \([c,d]\) 的后缀得到的,由于 \([a,d]\) 的权值和一定,所以只需要让 \([a,b]\) 的前缀、\([c,d]\) 的后缀分别最大即可。这个显然可以直接用线段树维护出来。
最后的问题就是怎样构建出每个数对应的 \(1,-1\) 序列,如果每一次都暴力建线段树肯定不行。考虑从大到小建树,这样每一次由 \(1\) 改为 \(-1\) 的位置总数只有 \(n\),所以每一次修改用主席树维护即可。
例 5 [FJOI2016] 神秘数
题意: 令一个可重数字集合 \(S\) 的神秘数为最小的不能被 \(S\) 的子集和表示的正整数。给定一个序列,求集合 \(\{a_i\mid i\in[l,r]\}\) 的神秘数。
首先需要发现一个性质。如果当前可重集可以表示出 \([1,lim]\) 的所有正整数,那么如果下一个加入的数字 \(a \le lim+1\),则可重集可表示的数字会扩展到 \([1,lim+a]\);否则该可重集的神秘数就是 \(lim+1\)。
证明如下:
当前可重集可以表示 \([1,lim]\) 的所有正整数,那么加入 \(a\) 后可以表示的正整数就应该是 \([1,lim]\cup [a,lim+a]\)。如果 \(a\le lim+1\),则上面的集合就是 \([1,lim+a]\);否则中间就会存在无法被表示的正整数,而这其中最小的就是 \(lim+1\)。
对于每一个询问,考虑暴力扩展当前的可重集。设当前可重集中包含了值域在 \([1,res]\) 中的所有数,它们可以表示所有在 \([1,lim]\) 中的正整数,那么下一次可以加入的数的范围应该是 \([res+1,lim+1]\)。设值域在这个区间中的所有数的和为 \(sum\),若 \(sum=0\),答案就是 \(lim+1\);否则当前可重集的值域范围会扩展至 \([1,lim+1]\),而它能表示的正整数范围则会扩大至 \([1,lim+sum]\)。
不难发现上面的过程中需要求解区间 \([l,r]\) 中值域在 \([res+1,lim+1]\) 的数的总和,这个就可以用主席树来实现了。最后的问题就是暴力扩展的时间复杂度,我们考虑 \(lim\) 的最大值是题目中给出的 \(10^9\),而每一次加上的 $sum $ 的最小值是 \(res+1\)。根据手玩可以发现,最后 \(sum\) 前的系数是一个类似斐波那契数列的东西,而斐波那契数列的数量级是 \(2^n\) 的,所以暴力扩展的复杂度是 \(O(\log \sum A_i)\),总复杂度 \(O(m\log n\log \sum A_i)\),可以通过。
例 6 [BZOJ4771] 七彩树
我们在这里介绍一下区间数颜色的基本方式,常见的有两种:
- 记录每个节点的 \(pre\),表示该节点颜色上一次出现的位置。对于区间 \([l,r]\),我们只计算区间中第一次出现的颜色,那么这些颜色对应的位置一定满足 \(pre_i< l\)。所以我们相当于求出 \(i\in[l,r],pre_i\in[0,l)\) 的点的个数,二维数点即可。
- 换一种思路,我们用扫描线和区间加法来做。当从 \(r\to r+1\) 的时候,区间 \((pre_{r+1},r+1]\) 这一段的颜色数量会加 \(1\),我们此时求的是后缀和,所以在 \(r+1\) 处加一,\(pre_{r+1}\) 处减一。再用树状数组维护后缀和即可。
对于此题来讲,第一种方法不是很好做,考虑第二种方法。我们按照 \(dep\) 来建立可持久化线段树(也就是第 \(k\) 个线段树维护 \(dep\le k\) 的点的信息),当增加一个点的时候,我们找到当前颜色中已经被插入的点按 DFS 序排名后该点的前驱和后继。根据 DFS 序的优良性质,可以知道这两个点和当前点的 \(\text{lca}\) 中更深的那个节点就是第一个会受到影响的节点,按照上面所说的第二种方式,我们在当前节点处加一,\(\text{lca}\) 处减一,最后求出子树和即可。
复杂度是 \(O(n\log n)\),可以通过。
1.3 拓展
我们在上面已经实现了可持久化线段树,实际上就是实现了一个可持久化数组。那么按照这个理论,所有使用数组的数据结构应该都能用可持久化线段树来维护。那么我们就有了另一种可持久化数据结构——可持久化并查集。
由于要可持久化,所以肯定不能路径压缩了,我们只能用按秩合并。开一个可持久化数组维护 \(fa\) 和 \(siz\) 信息,然后查询和修改时正常操作,记录新版本编号即可。由于按秩合并的复杂度是 \(O(\log n)\) 的,加上线段树自己的 \(O(\log n)\),总复杂度即为 \(O(n\log^2 n)\)。
2 可持久化平衡树
2.1 基本思想
可持久化平衡树所采用的平衡树一般都是 \(\text{FHQ-Treap}\),其没有旋转的特性使得我们可以轻易实现可持久化操作。
由于实际上其操作仅有 \(\text{Split}\) 和 \(\text{Merge}\) 两种,所以我们对这两个操作进行可持久化即可。具体来讲,在 \(\text{Split}\) 过程中,我们分裂出来的两颗树不是在原树上进行操作,而是新建根然后分裂。此时会发现,分裂出来的两棵树与原树有很大的重合,所以我们借鉴线段树可持久化的操作,对这些节点进行复用即可。
也就是说,我们只要复制我们走过的每一个节点即可完成可持久化。对于 \(\text{Merge}\) 操作同理,新建节点然后合并即可。
事实上,在某些情境下 \(\text{Merge}\) 操作不必新建节点,这取决于你维护的 \(\text{FHQ-Treap}\) 上相同的元素是算一个节点还是多个节点,也就是看你的节点权值有没有重复来决定的。若有重复则需要新建节点,否则不需要。
模板题:【模板】可持久化平衡树,代码如下:
#include <bits/stdc++.h>
using namespace std;
const int Maxn = 5e5 + 5;
const int Inf = 2147483647;
int n;
int rt[Maxn];
struct node {
int l, r, siz, val, key;
}t[Maxn * 80];//空间尽可能开大,因为空间复杂度并不是标准的 log
int tot = 0;
#define lp t[p].l
#define rp t[p].r
int newnode(int x) {
t[++tot] = {0, 0, 1, x, rand()};
return tot;
}
void pushup(int p) {
t[p].siz = t[lp].siz + t[rp].siz + 1;
}
void split(int p, int k, int &x, int &y) {
if(!p) {
x = y = 0;
return ;
}
if(t[p].val <= k) {
x = ++tot;//新建节点
t[x] = t[p];//复制
split(t[x].r, k, t[x].r, y);//找右子树,左子树全部复用
pushup(x);
}
else {
y = ++tot;//新建节点
t[y] = t[p]; //复制
split(t[y].l, k, x, t[y].l);//找左子树,右子树全部复用
pushup(y);
}
}
int merge(int x, int y) {
if(!x || !y) return x + y;
int rt = ++tot;//新建节点
if(t[x].key < t[y].key) {
t[rt] = t[x];
t[rt].r = merge(t[rt].r, y);
}
else {
t[rt] = t[y];
t[rt].l = merge(x, t[rt].l);
}
pushup(rt);
return rt;
}
int kth(int p, int k) {
if(t[lp].siz + 1 == k) return t[p].val;
if(k <= t[lp].siz) return kth(lp, k);
else return kth(rp, k - t[lp].siz - 1);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for(int i = 1; i <= n; i++) {
int v, opt, k;
cin >> v >> opt >> k;
switch(opt) {
case 1: {
int x, y;
split(rt[v], k, x, y);
rt[i] = merge(merge(x, newnode(k)), y);
break;
}
case 2: {
int x, y, z;
split(rt[v], k, x, z);
split(x, k - 1, x, y);
y = merge(t[y].l, t[y].r);
rt[i] = merge(merge(x, y), z);
break;
}
case 3: {
int x, y;
split(rt[v], k - 1, x, y);
cout << t[x].siz + 1 << '\n';
rt[i] = merge(x, y);
break;
}
case 4: {
cout << kth(rt[v], k) << '\n';
rt[i] = rt[v];
break;
}
case 5: {
int x, y;
split(rt[v], k - 1, x, y);
if(!x) cout << -Inf << '\n';
else cout << kth(x, t[x].siz) << '\n';
rt[i] = merge(x, y);
break;
}
case 6: {
int x, y;
split(rt[v], k, x, y);
if(!y) cout << Inf << '\n';
else cout << kth(y, 1) << '\n';
rt[i] = merge(x, y);
break;
}
}
}
return 0;
}
上面是权值平衡树的可持久化,对于区间平衡树也是如此,所以我们又有一道模板题:【模板】可持久化文艺平衡树。
发现我们做这道题唯一的难点在于懒标记的处理,如果直接下放可能会导致其他共用这个节点的树的信息改变,但是不下放的话这个标记并没有办法标记永久化。考虑到可持久化的实质其实就是在每一次修改的时候复制节点进行操作,所以我们下放标记的时候复制一遍左右儿子然后再交换即可。
所以下放标记的代码如下,其余部分是一致的:
struct node {
int l, r, val, siz, key, tag, sum;
}t[Maxn * 60];
#define lp t[p].l
#define rp t[p].r
int tot = 0;
int newnode(int x) {
t[++tot] = {0, 0, x, 1, rand(), 0, x};
return tot;
}
int copy(int p) {
int x = ++tot;
t[x] = t[p];
return x;
}
void pushdown(int p) {
if(!t[p].tag) return;
if(lp) lp = copy(lp), t[lp].tag ^= 1;
if(rp) rp = copy(rp), t[rp].tag ^= 1;
swap(lp, rp);
t[p].tag = 0 ;
}
当然由于这道题的下标肯定不同,所以平衡树上每个节点的权值一定不同,合并时可以不用新建节点。
2.2 例题
例 1 [HDU6087] Rikka with Sequence
首先发现操作 \(1,3\) 都较为容易解决,但是操作 \(2\) 不是特别容易。需要注意的是操作 \(2\) 并不是将 \([l-k,r-k]\) 平移挪到 \([l,r]\) 处,而是将 \([l-k,l-1]\) 这个区间一直复制,直到填满 \([l-k,r]\) 这个区间。
由于我们会一直复制,所以暴力做的复杂度肯定会炸。考虑到每一次复制的区间相同,所以可以倍增优化之。容易发现操作 \(3\) 中的分裂操作要求保留分裂出来的数组和原数组,操作 \(2\) 中复制区间时两颗树会有重复节点,所以使用可持久化平衡树来维护即可。
然后对于此题这些还不够,我们还有以下优化:
- 由于我们会合并两颗完全一样的树,所以如果按照传统的赋随机值的方式来判断谁挂在谁下面会多次出现相同的值,导致时间较劣。考虑在合并时用随机值判断,让子树大小更大的节点成为父亲的概率更高,这样可以让树更加平衡一些。
- 容易发现此题中空间有足足 \(64\text{MiB}\),所以我们如果直接按照上面的做法做的话空间会炸,原因在于有一些节点被删除后是无用的,但是依然占用空间。我们给节点数量设置一个阈值,当节点数量过大的时候,跑出当前的 \(a\) 数组,然后清空平衡树暴力重构即可。
为了保证正确性,建议此题中的所有 \(\text{Merge}\) 都开新节点,尽管有一些不用。
3 可持久化字典树
3.1 基本思想
可持久化字典树的思想和上面两种数据结构依然一致,容易发现,当我们插入一个字符串的时候,我们只会修改这条路径上节点的信息,而别的地方我们不会加以理睬。所以对于没有修改的地方,我们直接复用上一次的节点即可。
大部分情况下,可持久化字典树使用的都是 \(\text{0-1 Trie}\),当然也有例外。
3.2 例题
例 1 [BZOJ3261] 最大异或和
容易将区间的异或转化为两个前缀异或和的异或。也就是 \(s_{p-1}\oplus s_n\oplus x\)。发现后面的值是定值,所以实际上就是查询区间 \([l-1,r-1]\) 中 \(s_p\) 异或 \(s_n\oplus x\) 的最大值。
考虑到没有区间限制的时候,我们就是每一次尽可能往与当前位不同的那一位上走。现在有了区间的限制,我们就需要知道这个区间内所有数构成的字典树上的信息。考虑运用主席树的思想,每一次插入一个数后建可持久化字典树,然后两个点之间作差就可以知道当前节点在这个区间内的出现次数,以此来判断能不能走到该节点然后求答案即可。
代码如下:
#include <bits/stdc++.h>
using namespace std;
const int Maxn = 6e5 + 5;
const int Inf = 2e9;
int n, q, a[Maxn];
int sum[Maxn];
int rt[Maxn];
namespace Trie {
struct node {
int son[2], siz;
}t[Maxn * 25];
int tot = 0;
int insert(int p, int x) {//在上一个版本的基础上建字典树
int rt = ++tot, ret = rt;
for(int i = 25; i >= 0; i--) {
int ch = (x >> i) & 1;
t[rt] = t[p];
t[rt].siz++;
t[rt].son[ch] = ++tot;
rt = t[rt].son[ch];
p = t[p].son[ch];
}
t[rt] = t[p];
t[rt].siz++;
return ret;
}
int query(int p, int q, int x) {//两颗字典树作差得到当前区间的字典树
int ans = 0;
for(int i = 25; i >= 0; i--) {
int ch = (x >> i) & 1;
if(t[t[q].son[ch ^ 1]].siz - t[t[p].son[ch ^ 1]].siz) {//有节点才能跳
ans += (1 << i);
p = t[p].son[ch ^ 1];
q = t[q].son[ch ^ 1];
}
else {
p = t[p].son[ch];
q = t[q].son[ch];
}
}
return ans;
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> q;
rt[0] = Trie::insert(rt[0], 0);//先插入 0
for(int i = 1; i <= n; i++) {
cin >> a[i];
sum[i] = sum[i - 1] ^ a[i];
rt[i] = Trie::insert(rt[i - 1], sum[i]);
}
while(q--) {
char opt;
int l, r, x;
cin >> opt;
switch(opt) {
case 'A': {
cin >> x;
a[++n] = x;
sum[n] = sum[n - 1] ^ a[n];
rt[n] = Trie::insert(rt[n - 1], sum[n]);
break;
}
case 'Q': {
cin >> l >> r >> x;
l--, r--;
if(!l) cout << Trie::query(0, rt[r], sum[n] ^ x) << '\n';
else cout << Trie::query(rt[l - 1], rt[r], sum[n] ^ x) << '\n';
break;
}
}
}
return 0;
}
例 2 [BZOJ2741] Fotile 模拟赛 L
最大异或和仍然可以考虑上一题的方式,但是如果直接暴力枚举并求解的话复杂度是 \(O(nm\log V)\),难以通过。
考虑序列没有修改操作,所以可以进行预处理,这时可以想到分块。预处理出 \(mx(l,r)\) 表示区间端点在第 \(l\) 个块到 \(r\) 位置之间的最优答案。转移显然可以从 \(mx(l,r-1)\) 转移过来,用可持久化字典树求出以 \(r\) 为右端点的最优答案即可。
查答案的时候只需要对散块暴力查询即可,仍然运用可持久化字典树。设块长为 \(B\),复杂度为 \(O(n\cdot \dfrac nB\cdot \log V+mB\log V)\)。取 \(B=\sqrt{n}\) 即可,复杂度为 \(O(n\sqrt n\log V)\)。
例 3 [THUSC2015] 异或运算
发现这居然是求矩阵中的第 \(k\) 大值,那么直接考虑二分。我们先想想对于一个固定的 \(x\),找出一段区间内的 \(y\) 与 \(x\) 异或后的第 \(k\) 大值怎么做,显然可以在可持久化字典树上二分,每次判断一下当前位取到 \(1\) 的大小并与 \(k\) 比较即可。复杂度 \(O(\log V)\)。
然后考虑给出了一段 \(x\) 之后怎么做,不难发现题目中的 \(x\) 只有 \(1000\) 个,所以暴力枚举后跑多重根的二分即可,复杂度 \(O(pn\log V)\)。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号