2024.4 做题记录
2024.4 做题记录
[NOIP2018 提高组] 旅行
看到题目中要求 \(m=n\) 或 \(m=n-1\),此时就应当分类讨论。
① 当 \(m=n-1\) 时:
此时数据为一颗树。
我们贪心的想:起始点为 \(1\) 的时候显然最优。对于每一个节点,在它子树内按照从小到大的顺序遍历显然最优。
复杂度 \(O(n \log n)\),瓶颈在于排序。因此可以将快速排序换为其他排序达到 \(O(n)\) 的效果,然而并没有这个必要。
② 当 \(m=n\) 时:
此时数据为一颗基环树。
\(O(n^2)\) 做法:
我们先找出环,然后考虑枚举这个环上的一条边,将这条边删去后就与情况 ① 相同。而此时枚举完所有边,将答案取最小即可。
复杂度 \(O(n^2)\)。可以通过原数据,但有更优的做法。
\(O(n \log n)\) 做法:
我们考虑,本题的关键在于:当走到一个环上的时候,从哪一个点 \(p\) 回溯?因为当我们从 \(p\) 回溯,相当于删掉了 \(p\to to_p\) 这条边。如果能解决这个问题,就可以保证在一次 DFS 内求出答案。
考虑什么时候回溯。首先想到的是当走下一个节点不如回溯之后走到的第一个节点,那么必然要回溯。但是这并不一定。如果这个节点不是父亲节点所有出点中最大的,那么回溯之后要走一个比当前点还要大的点,显然更劣。
因此,回溯的条件是:当这个节点是父亲节点所有出点中最大的,并且还要大于回溯后走到的第一个节点。
具体实现可以记录回溯后走到的第一个节点,记录是否回溯来实现。
复杂度 \(O(n\log n)\),瓶颈仍然在于排序。
[IOI2008] Island
首先,观察题目以及样例,发现有些玄妙。我们先不管船,单独看桥会发现一个联通块内的答案就是树的直径。然后来看船,显然对于任意一个联通块内的节点都不能使用船,因此船只能用于两个联通块之间的交通,并且每个联通块只能走一遍。
再次观察题目会发现边数等于点数,即整个图是基环树森林,于是最后这道题就可以转化为:
给出几颗基环树,求出其直径之和。
其实这是一道板子,不过可以写一下。
考虑环形 dp 处理方式,首先对于一颗基环树,看做一个环上挂着一些树。对于子树内求出最长链的长度,然后作为环上这个点的点权;现在我门有点权 \(p\) 和边权 \(w\),那么要选出两个点 \(u,v\),满足 \(p_u+p_v+dis(u,v)\) 最大。
此时这个式子要在环上 dp,这时考虑朴素的处理方式——断环为链。此时在设 \(dp(i)\) 表示第二个节点选在 \(i\) 的值,那么方程就是:
其中 \(cnt\) 为环上节点数量。发现 \(dis(i,j)\) 可以 \(O(n)\) 前缀和求出,然而暴力枚举这个式子的复杂度仍然是 \(O(n^2)\)。
发现取 \(\max\) 的范围是一段长度固定的区间,自然想到单调队列优化 dp。令 \(sw_i\) 为边权前缀和,式子可以化为 \(dp(i)=\max_{i-cnt+1\le j \le i-1}\{p_j-sw_j\}+p_i+sw_i\)。维护 \(p_j-sw_j\) 即可。
最后取 dp 最大值,然后累加答案即可。
剩下的还要注意很多细节:
- 基环树的直径可能就是一颗子树的直径,因此在 dp 过程中还可以记录次长链直接求出子树直径。
- 边权有 \(10^8\),因此要开
long long。 - 单调队列优化 dp 的时候注意赋初始值。
[POI2012] RAN-Rendezvous
首先这是一颗基环外向树森林,因此分类讨论:
- 当两个点不在同一颗基环外向树时,显然没有答案,输出
-1 -1即可。 - 当两个点在环上同一个点的子树内,答案就是两者的 LCA,随便用一种方式维护即可。
- 当两个点在环上不同点的子树内,两者都先走到各自在环上的节点。接下来由于是在环上,所以无论从哪一个走到哪一个都有可能,因此求出两个答案后取最优的即可。
[hdu6305] RMQ Similar Sequence
首先看到要求期望,那我们先将他拆开。即一个数列之和的期望以及数列符合 RMQ 相似的概率。二者乘积即为答案。
先看第一部分,这一部分较为简单。对于每一个数,在 \([0,1]\) 内随机选择,显然期望为 \(\dfrac 12\),又由于总长度为 \(n\),所以和的期望就是 \(\dfrac n2\)。
接下来是 RMQ 相似的概率。这一步需要想到笛卡尔树,我们建立 \((i,{a_i})\) 的大根笛卡尔树,这样根据性质可得根节点就是区间的最大值。那么要求所有区间最大值都是这个数,只需要要求根节点编号一致即可。设一个根节点的子树大小为 \(\text{siz}_i\),那么根节点最大的概率就是 \(\dfrac 1{\text{siz}_i}\)。
两者相乘可得答案为 \(\dfrac n{2\prod\limits_{i=1}^n\text{siz}_i}\)。
[COCI2008-2009#4] PERIODNI
这道题与笛卡尔树的经典板题 最大子矩形 有些相似,但是又有区别。
首先建立出 \((i,h_i)\) 的小根笛卡尔树,然后我们考虑切分整个图形。由笛卡尔树性质可以得到,每个节点都会对应一个完整的矩形,如下图:
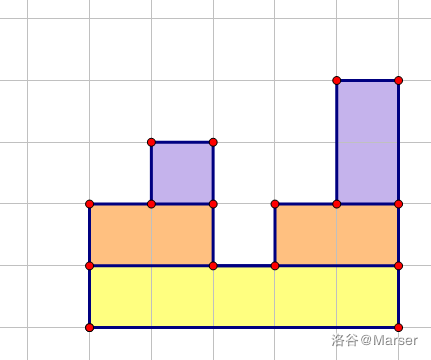
接下来我们直接在笛卡尔树上讨论问题。根据计算得到,一个节点对应的矩形的长就是 \(\text{siz}_i\),宽就是 \(|h_i-h_{fa}|\)。
那么我们又会发现,子树中所有节点对应的矩形都在该节点对应矩形的上方。因此当子树中其他节点对应的矩形中放了 \(x\) 个点的时候,该矩形能放点的长就会变为 \(\text{siz}_i-x\)。
然后考虑怎样计算答案,需要亿点树形 dp。设 \(dp(i,j)\) 表示根为 \(i\) 的子树中选取 \(j\) 个点的方案数。那么枚举左右儿子选点数量,可以得到方程:
这个式子爆算是 \(O(nk^2)\) 的,无法通过。不过我们会敏锐的发现当中有两项与 \(j\) 无关,将他们提出去以后可以得到:
显然后一部分可以 \(O(k^2)\) 预处理,前一部分 \(O(nk)\) 计算,最后复杂度是 \(O(n^2)\) 级别的,可以通过。
[hdu6854] Kcats
首先看到这个单调栈就可以想到笛卡尔树。那么我们先以 \((i,p_i)\) 建立小根笛卡尔树,接下来需要发现一条性质:
性质:对于 \(i\),\(a_i\) 就是所有节点中深度小于 \(i\) 号点的点中,下标小于 \(i\) 的个数加一。
证明:由于 \(p_i\) 满足小根堆性质,因此只要深度小于 \(p_i\),就代表权值小于 \(p_i\),也就意味着在单调栈中会在 \(i\) 的底下。同时还要满足这些数出现在 \(i\) 以前,因此下标也要小于 \(i\)。最后加上的一个 \(1\) 就是 \(i\) 本身。
那么有了这条性质可以干什么呢?
我们知道,笛卡尔树上节点子树对应一段区间。而下标是具有二叉搜索树性质的,因此左子树答案就是该节点答案,右子树答案是该节点答案加一。而根节点不确定,因此要枚举根节点,将区间砍成两端。
看到这些会想到什么?区间 dp。设 \(dp(l,r,d)\) 表示区间 \([l,r]\) 所对应的根节点满足性质的点有 \(d\) 个的方案数。那么此时方程就比较显然了:
最后的组合数表示选出左子树的方案数。
但是还有可能 \(p_rt=-1\),那么此时我们就枚举 \(p_{rt}\) 的值然后转移即可。
初始化为 \(dp(i,i,p_i)=1\),答案为 \(dp(1,n,1)\)。
[poj2482] 窗内的星星
首先考虑将一颗星星转化为一个矩阵。我们考虑右上角的范围,会初步发现当右上角所在的 \((x_1,y_1)\) 与当前点 \((x,y)\) 满足 \(x<x_1<x+w\) 且 \(y<y_1<y+h\) 时满足要求。
问题是我们不能在构建矩形的时候带上小于号。考虑转化。如果矩形右上角所在的点 \((x_2,y_2)\) 满足 \(x\le x_2\le x + w - 1\) 且 \(y\le y_2\le y + h-1\) 时,令 \(x_1=x_2+0.5,y_1=y_2+0.5\),此时绝对仍然满足条件。
我们不需要求出矩形个数,因此这样做是正确的。
那么现在我们就按照这个构建矩形,每个矩形的上下边的权值就是 \(c,-c\)。然后进行扫描线。
此时维护的是区间最大值以及区间修改,使用懒标记即可。
但是我们又会发现一个问题:按传统扫描线的存线段的方式无法使用,因为此时求的是点的信息。因此我们将线段树改为存储每一个点的值即可。
[USACO12OPEN] Balanced Cow Subsets G
首先看到 \(n \le 20\),想到爆搜。
我们考虑一个数的状态,有三种:放入左边集合,放入右边集合,不放入集合。
总共有三种情况,也就是复杂度 \(O(3^n)\),显然爆炸。
考虑折半搜索。这样我们记录下每次集合中的状态。设第一次搜索放入左边集合的数字之和为 \(a\),放入右边集合的数字之和为 \(b\);第二次搜索放入左边集合的数字之和为 \(x\),放入右边集合的数字之和为 \(y\)。那么会有 \(a+x=b+y\)。我们要将同一次搜索的数放在一次,于是移项得 \(a-b=y-x\)。分别维护即可。
但是如果简单这样枚举,会发现有重复情况。因为一个数放入左右集合都是放入了集合,因此我们还需要去重。考虑状压,每次记录二进制串,然后用离散化去重即可。
[SDOI2015] 寻宝游戏
其实和虚树关系不大,只运用到了一点思想。
首先考虑所有关键点走一遍的边权之和,由于原图是一棵树,因此每条边都会被走两边。同时,我们可以得到如下式子:
当我们将 \(a_i\) 按照 DFS 序排序后,就是按照每一个点的顺序走完全程。这里钦定 \(a_{n+1}=a_1\)。
接下来考虑计算答案,显然不能每次统计,需要求出一个点的修改对于答案的贡献。
先以加点为例,显然我们需要找到在原式中和他连接的两个点。设这个点为 \(x\),那么 \(y\) 就是 DFS 序比 \(x\) 小且 DFS 序最大的数(也就是 DFS 序上 \(x\) 的前驱),\(z\) 为 DFS 序上 \(x\) 的后继。显然会发现,原式中会多出 \(\mathrm{dist}(y,x)+\mathrm{dist}(x,z)\),减少了 \(\mathrm{dist}(y,z)\),因此加点的贡献就是:
删去点同理,改变符号即可。
现在考虑维护这个东西,我们需要查询 DFS 序的前驱、后继,还要支持动态插入和删除一个数。这不就是平衡树板题吗,用 FHQ 维护即可。
当然我们也可以用 STL 自带的 set 简单处理。
[ZJOI2019] 语言
首先将答案转化为每个点的贡献,也就是要求出这个点可以到达多少个点。
设这个答案为 \(S_x\),我们就是要求出 \(\sum\limits_{i=1}^nS_i\)。
不难发现对于一个点 \(x\),能够到达的点构成了一颗树,同时这棵树上一定包含一部分路径的 \(s_i,t_i\)。
因此其实 \(S_x\) 就是包含 \(x\) 的所有路径的 \(s_i,t_i\) 所构成的最小子树的边数。
此时我们需要看一个小小的经典结论:
引理:树上 \(n\) 个关键点之间形成的最小联通子树的大小为 \(\sum\limits_{i=1}^n \operatorname{dep}_{a_i}-\sum\limits_{i=2}^{n}\operatorname{dep}_{\operatorname{lca}(a_i,a_i-1)}-{\operatorname{dep}_{\operatorname{lca}(a_1,a_2,a_3,\cdots,a_n)}}\)(按 DFS 序排序后)。
我们考虑将 \(a_i\) 按照 DFS 序排序后一一加入联通子树。当我们加入第 \(i\) 个点时,由于 DFS 是升序的,所以此时 \(\operatorname{lca}(a_i,a_i-1)\) 就是离 \(a_i\) 最近的点,算出两者间距离即可。最后还要减去所有点的 lca 的深度。
于是我们就可以暴力计算出 \(S_x\) 了。
我们考虑对于每个点记录一个桶,桶的下标是 DFS 序。当桶的元素为 \(1\) 时就表明 DFS 序为这个下标的点属于关键点。这样就相当于对关键点进行桶排序。
然后接下来我们考虑优化,对于 \(s_i,t_i\) 构成的链,理论上要将所有点的桶的 \(dfn_{s_i},dfn_{t_i}\) 都加一。但是我们想到这是树链,自然想到树上差分。
那么由于我们进行了树上差分,就必须要合并。那么要合并的东西是一个数组,显然直接合并 \(O(n)\) 无法承受。
这时会想到什么?对于每个点的数组单点修改,然后进行合并。这不就是线段树合并板题吗!
因此对于每一个点,维护一颗线段树表示 DFS 序的桶,在线段树上操作一下即可。
注意这样算没有考虑大小关系,因此要除以二。
时间复杂度 \(O(n\log^2 n)\)。
[HNOI2014] 世界树
首先虚树的操作是显然的,问题就在于建出虚树后怎么做。这里我们采用 \(5\) 个 DFS 解决。
首先我们需要求出每个点所对应的议事处,然后计算这个点对该议事处的贡献即可。
我们接下来需要分类讨论:
一、对于在虚树上的点:
可以通过两次 DFS 求出这个点的议事处,即 up and down。
具体的,第一次 DFS 按照路径长度求出子树内到自己最近的议事处,第二次 DFS 求出子树外到自己最近的议事处,两者取较小值即可。不再赘述。
二、对于不在虚树上的点:
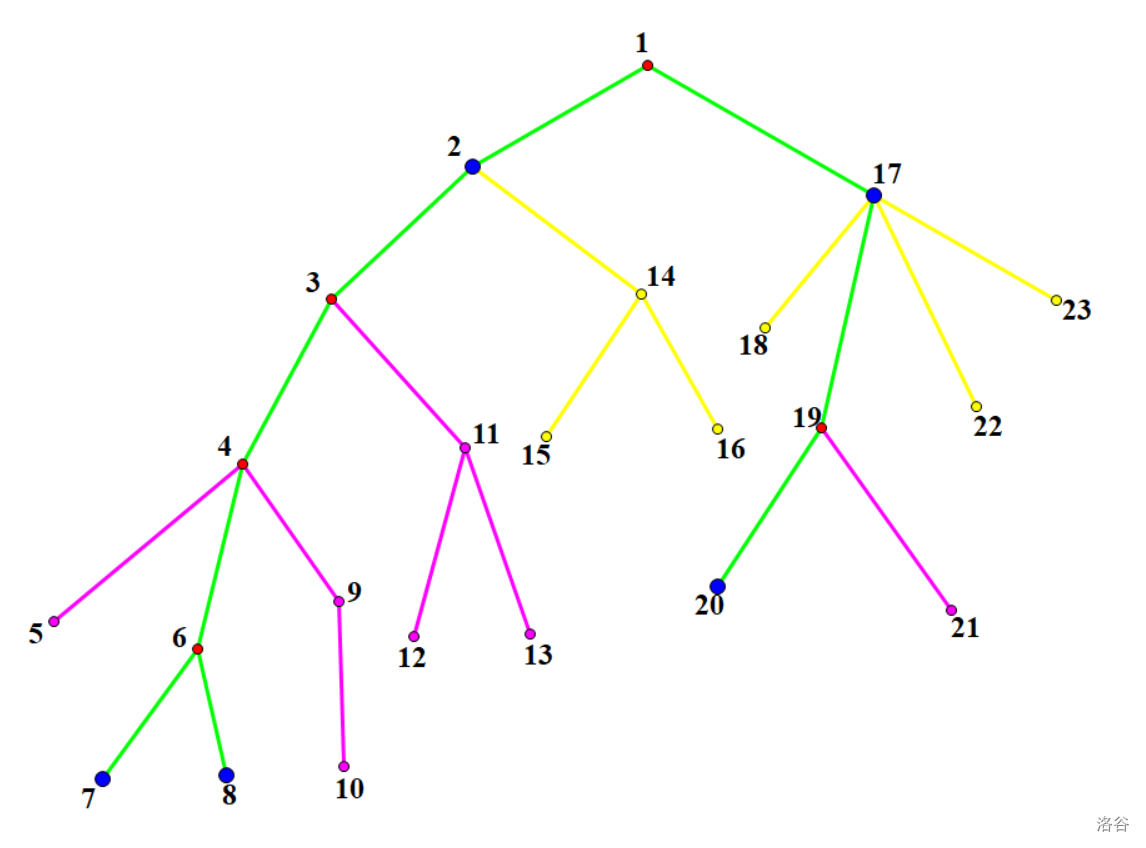
图中蓝色点为关键点,绿色边表示虚树边。
这一部分才是我们讨论的重点,再次分类讨论:
① 对于是虚树上的点的子树中的点(即黄色点)
那么此时我们只需要计算出这个点除掉在虚树上的子树的子树大小,将这个加到对应议事处的答案上即可。这个可以运用第三个 DFS 解决。
有一个小问题在于:如何除掉这个点在虚树上的子树?
假如现在遍历到点 \(2\),很显然我们要除掉 \(3\) 的子树大小。问题是虚树上并没有 \(2\) 的儿子信息。
其实这个问题也很简单:发现 \(2\) 在虚树上的儿子为 \(6\),那么 \(2\) 在 \(6\) 方向上的儿子其实就是 \(6\) 的 \(dep_6-dep_2-1\) 级祖先。
利用倍增求解即可(这就意味着树剖性价比不高了)
② 对于不是虚树上的点的子树中的点(即绿色点)
此时我们就是要处理虚树上两点 \(x,y\) 在原树上中间隔的点。运用第四个 DFS 解决。
还需要分类讨论:
- \(bel_x=bel_y\)
显然整个中间这一部分都是 \(bel_x\) 的,用子树大小计算即可。
- \(bel_x\ne bel_y\)
此时我们扩大一下视野,就是要把 \(bel_x\) 和 \(bel_y\) 之间的链劈成两半,然后一半给 \(bel_x\),一半给 \(bel_y\)。
这里我们利用二分简单查找一下即可。
最后我们输出所有议事处的答案即可。然后由于有多测,所以我们还需要用第五个 DFS 清空所有数组。
(其实算上倍增 LCA 的一个 DFS 总共有 \(6\) 个 DFS)
[BJOI2017] 树的难题
首先容易想到点分治,问题在于如何统计经过点 \(x\) 的路径数量。
首先我们可以维护每条根链上的权值以及长度。先考虑更简单的情况,即不考虑颜色段的情况。
这时求法是显然的,考虑维护一颗线段树,下标为链长度,然后对于当前根链在线段树上的特定区间内直接查询即可。
接下来考虑维护颜色段,我们发现,对于末尾颜色相同的两条根链,需要在求和后减去该颜色对应的权值;而颜色不同则不需要。
我们考虑对于每一种颜色维护一颗线段树,但是这样复杂度过高。
考虑我们并不需要知道每种颜色的具体信息,只需要知道所有与他不同的颜色即可。因此实际只需要维护两颗线段树:颜色与当前根链相同的,颜色与当前根链不同的。
然而我们不能在颜色改变的时候简单维护这两颗线段树,考虑将颜色排序,在同一颜色之内只需要修改第二颗线段树。当颜色发生改变时,只需要将第二颗线段树的信息合并到第一颗线段树上,然后清空第二颗线段树即可。
考虑到需要实现清空以及合并操作,采用动态开点线段树更为简单。复杂度 \(O(n\log n)\)。
[BZOJ3697] 采药人的路径
首先还是考虑点分治,但是我们发现合法的路径条数并不好求。
不好求的原因在于我们需要一个休息点,这个并不能够简单求解。
我们先转化题意,将 \(0\) 改为 \(-1\),这样合法路径上的权值之和就是 \(0\)。
我们想到点分治的本质是不断将当前子树信息与之前的子树信息合并,考虑这样的 dp 思想:我们设 \(dp(i,0)\) 表示在当前子树之前的所有子树中,根链路径长度为 \(i\),且是这条路径所在的链上第一次路径长度和为 \(i\) 的路径数量。而 \(dp(i,1)\) 则表示当前子树之前的所有子树中,根链路径长度为 \(i\),且不是这条路径所在的链上第一次路径长度和为 \(i\) 的路径数量(也就是有祖先节点的根链长度也为 \(i\))。
在这样的 dp 思想下,我们会发现一些性质,例如对于下图:

假设 \(u'\) 是这条根链上第一次出现路径为 \(p\),\(u\) 为第二次出现。\(v',v\) 同理,路径和为 \(q\)。
此时我们就知道。在 \(u\to u'\) 这一条链上,权值之和一定为 \(0\)。那我们结合合法路径的性质,这就是一条关键路径。如果 \(q=-p\),那么从 \(u'\to v'\) 或 \(u'\to v\) 的权值之和也为 \(0\)。那么这样我们就能构造出一条经过根节点,且有休息点(\(u'\))的完整合法路径了。
同理,当我们从 \(u'\) 开始想找出这样的一条合法路径,只要 \(q=-p\) ,那么 \(u'\to v\) 就是另一条完整合法路径,休息点为 \(v'\)。
那么我们便可以总结如下:
- 如果当前节点对应的路径之和 \(p\) 是第一次出现的话,就需要找到前面路径之和为 \(-p\) 且不是第一次出现 \(-p\) 的点。根据 dp 状态,可知答案就是 \(dp(-p,1)\)。
- 如果当前节点对应的路径之和 \(p\) 不是第一次出现的话,我们只需要找到路径之和为 \(-p\) 的即可,答案为 \(dp(-p,0)+dp(-p,1)\)。
但是这样我们还没有讨论完全,当 \(p=0\) 时这样做并不对。
- 如果当前节点对应的路径之和 \(0\) 是第一次出现的话,我们只需要找到前面路径之和为 \(0\) 的即可,答案为 \(dp(0,0)+dp(0,1)\)。
- 如果当前节点对应的路径之和 \(0\) 不是第一次出现的话,它肯定可以和前面路径之和为 \(0\) 的构成完整合法路径,但是同时这条链本身也就是一个完整合法路径,因此此时答案为 \(dp(0,0)+dp(0,1)+1\)。
我们在点分治的时候维护 dp 数组即可。
[HNOI2015] 开店
首先发现题目求的是 \(\sum\limits_{l\le x_i\le r}dis(i, u)\)。按照点分树的传统思路拆式子,得:
此时我们在每个点 \(x\) 上要维护三个东西:
- \(v1\):下标为 \(i\) 表示 \(\sum\limits_{x_p=i}dis(x, p)\)
- \(v2\):下标为 \(i\) 表示 \(\sum\limits_{x_p=i}dis(fa_x,p)\)
- \(v3\):下标为 \(i\) 表示 \(\sum\limits_{x_p=i}1\)
那么答案式子就可以抽象转化为 \(v2-v1+v3\times dis(q, u)\)。
我们试图使用线段树维护这些信息,然而我们发现 \(x_p\) 是 \(10^9\) 的。考虑离散化,但是这样失去了原数据的大小关系,同时常数也过大。
我们发现此题并没有修改操作,因此使用线段树大可不必。考虑 vector,用二元组存储 \(i\) 以及对应的值。
我们将 \(i\) 排序,接下来要找出对应的 \(l,r\),显然使用二分即可。然后利用前缀和求出区间对应的和。
但是这道题有一些卡常数。我们发现 \(v3\) 与 \(v1\) 是本质相同的,只要 \(v1\) 上有值那么 \(v3\) 就是 \(1\)。因此 \(v3\) 其实就是二分后 vector 中元素的个数。
[ZJOI2015] 幻想乡战略游戏
首先从暴力入手。可以考虑枚举每一个点到树上其他点的距离,这样做是 \(O(qn^2)\) 的。
我们考虑这与树上路径有关,并且还带有修改操作,因此想到点分树。我们可以用点分树维护每一个点到树上其他点的距离之和,时间复杂度就是 \(O(qn\log^2 n)\) 的,比刚才优秀一些,不过仍然无法通过。
我们考虑原树上的一些性质。假如我们当前以点 \(u\) 为答案,它的一个儿子为 \(v\)。那么什么时候取 \(v\) 比取 \(u\) 更优呢?
我们考虑将 \(u\) 改为 \(v\) 导致的答案的变化。具体的,\(v\) 子树内的节点的距离都会减少 \(dis(u,v)\),除此之外所有的距离都会增加 \(dis(u, v)\)。设 \(sd_x\) 表示 \(x\) 子树内所有点权之和,那么答案的差就是 \(dis(u,v)\times (sd_u-sd_v)-dis(u,v)\times sd_v\)。如果 \(v\) 更优,那么上面的式子就会小于 \(0\)。移项后得到 \(v\) 比 \(u\) 更优的条件:
考虑这样一件事:假设有两个点 \(v,w\),都满足比 \(u\) 更优。那么就会有 \(2sd_v>sd_u,2sd_w>sd_u\),即 \(2(sd_v+sd_w)>2sd_u\),得到 \(sd_v+sd_w>sd_u\)。然而 \(v,w\) 都是 \(u\) 的儿子,显然这个式子不可能成立。
这说明什么呢?很简单,对于一个节点 \(u\),至多只会有一个儿子比自己更优。
此时我们就可以考虑这样的做法:枚举每个点的儿子,如果儿子更优则进入儿子,反之计算自己的答案。计算答案就使用点分树。
我们考虑这样做的复杂度,显然这与树高有关,设树高为 \(d\),则复杂度为 \(O(q20d\log^2 n)\)。
如果树被卡成一条链,那么显然 \(d\) 就变成 \(n\) 了,复杂度不够优秀。但是我们可以控制树高,显然在点分树上做就可以保证时间复杂度。
但是在点分树上没有原树的儿子信息,这时我们对于每个节点记录一个 \(near\),表示这个节点在点分树子树内在原树上距离它的点分树上父亲最近的点,也就是点分树上父亲的原树的儿子。计算完儿子后,如果更优就进入儿子所在的重心。
这样我们的复杂度就是 \(O(20q\log^3 n)\),非常优秀。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号