平衡树

1 二叉搜索树

1.1 定义

二叉搜索树（Binary Sort Tree，BST）是一种二叉树的树形数据结构，定义如下：

空树是一颗二叉搜索树。
若二叉搜索树的左子树不为空，则其左子树上的所有点的权值都小于根节点的值。
若二叉搜索树的右子树不为空，则其右子树上的所有点的权值都大于根节点的值。
二叉搜索树的左右儿子都是二叉搜索树。

1.2 特性

在一般情况下，二叉搜索树插入和查询复杂度为 \(O(\log n)\)。但在一些特殊的情况下，例如插入序列单增时，二叉搜索树会被卡到近似一条链。此时其复杂度会退化到 \(O(n)\)。

我们有一条性质：当二叉搜索树深度最小时，二叉搜索树的最高复杂度最低。

因此我们要在保留二叉搜索树的特性同时，使其深度尽可能小。这种维护二叉搜索树“平衡”的数据结构，就是平衡树。

一般的平衡树有 Treap，Splay，AVL，红黑树等等。

下面详细介绍它们。

2 Treap

2.1 概述

Treap = Tree + Heap。顾名思义，就是 BST 和堆组合而成的数据结构。相比较与其他平衡树而言，Treap 实现起来较为简单。

2.1.1 Treap 的性质

Treap 是一颗完全二叉树，且 Treap 上每一个点有权值和优先级。其中优先级在加点中被随机赋予。
Treap 上每一个点的左右儿子的优先级均不大于或不小于当前点的优先级（满足堆的性质）。

2.2 有旋 Treap

2.2.1 旋转

有旋 Treap 使用旋转来维护平衡。

考虑二叉搜索树的这样一个性质：在只考虑 \(i,j\) 两点的情况下，\(i\) 为 \(j\) 的左儿子等价于 \(j\) 为 \(i\) 的右儿子。反之亦然。

我们假设要交换两点 \(i,j\)，假设 \(j\) 为 \(i\) 的左儿子，那么我们要将 \(i\) 变为 \(j\) 的右儿子。由于 \(i\) 顶替了 \(j\) 的右儿子的位置，所以让 \(j\) 的右儿子变成 \(i\) 的左儿子。

因此有如下定义：

将节点 \(i\) 的左儿子变为根节点，称为右旋。
将节点 \(i\) 的右儿子变为根节点，称为左旋。

因此我们可以用旋转操作维护堆的性质。我们指定优先级满足小根堆性质。

代码如下：

首先定义结构体，需要维护的信息是左右儿子、权值、当前权值出现的次数、优先级、子树节点个数。

struct Treap {
	int son[2], val, cnt, key, size;
}t[Maxn];

接下来完成旋转操作，在旋转完后维护子树节点个数。

void update(int p) {//更新子树节点个数 
	t[p].size = t[lp].size + t[rp].size + t[p].cnt;
}

void rotate(int &p, int d) {//d为方向，1为左旋，0 为右旋 
	int tmp = t[p].son[d ^ 1];
	t[p].son[d ^ 1] = t[tmp].son[d];
	t[tmp].son[d] = p;
	update(p);
	p = tmp;//更新当前根节点 
}

2.2.2 插入

当我们插入一个节点，如果这个点的优先级小于父亲的优先级，就要交换他和父亲。利用旋转交换即可。

void insert(int &p, int x) {
	if(!p) {//如果有可以直接放入的空位 
		p = ++tot;
		t[p].size = t[p].cnt = 1;
		t[p].val = x;
		t[p].key = rand();
		return ;
	}
	if(t[p].val == x) {//已有当前节点 
		t[p].cnt++;
		t[p].size++;
		return ;
	}
	int d = (x > t[p].val);
	insert(t[p].son[d], x);
	if(t[p].key > t[t[p].son[d]].key) {
		rotate(p, d ^ 1);
	}
	update(p);
}

2.2.3 删除

我们考虑用堆的方法删除。我们将要删除的点与他优先级较小的点交换，直到其变为叶子结点，就直接删除该点。

void del(int &p, int x) {
	if(!p) return;//没有该节点 
	if(x < t[p].val) {
		del(lp, x)//查左子树 
	}
	else if(x > t[p].val) {
		del(rp, x);//查右子树 
	}
	else {//已经找到 
		if(!lp && !rp) {//叶子结点 
			t[p].cnt--;
			t[p].size--;
			if(t[p].cnt == 0) {
				p = 0;
			}
		}
		else if(lp && !rp) {//左子树不空 
			rotate(p, 1)//左旋
			del(rp, x);
		}
		else if(!lp && rp) {//右子树不空 
			rotate(p, 0);//右旋 
			del(lp, x);
		}
		else {
			int d = (t[lp].key < t[rp].ley);
			rotate(p, d);//向优先级高的旋
			del(t[p].son[d], x); 
		}
	}
	update(p);
}

2.2.4 查询排名

直接计算该子树中小于 val 的节点个数 + 1。

int ask(int p, int x) {
	if(!p) return 1;//空节点
	if(t[p].val == x) {//当前点权值等于 x 
		return t[lp].size + 1;
	} 
	else if(t[p].val < x) {//当前点权值小于 x 
		return ask(rp, x) + t[lp].size + t[p].cnt;
	}
	else {//当前点圈住大于 x 
		return ask(lp, x);
	}
}

2.2.5 查询值

只需要判断出当前排名在树的哪个部分即可，类似于权值线段树。

int find(int p, int x) {
	if(!p) return 0;//空节点
	if(t[lp].size >= x) {//当前点排名大于 x 
		return find(lp, x);
	} 
	else if(t[lp].size + t[p].cnt < x) {//当前点排名小于 x 
		return find(rp, x - t[lp].size - t[p].cnt);
	}
	else {//当前点排名就是 x 
		return t[p].val;
	}
}

2.2.6 求前驱

利用二叉搜索树的性质求即可。

int pre(int p, int x) {
	if(!p) return INT_MIN;//空节点
	if(t[p].val >= x) {//权值大于等于 x 
		return pre(lp, x);//搜索左子树 
	}
	else {
		return max(t[p].val, pre(rp, x));
	}
}

2.2.7 求后继

同上。

int nxt(int p, int x) {
	if(!p) return INT_MAX;//空节点
	if(t[p].val <= x) {//权值小于等于 x  
		return nxt(rp, x);//搜索左子树 
	} 
	else {
		return min(t[p].val, nxt(lp, x));
	}
}

2.2.8 完整代码

P3369 【模板】普通平衡树 AC 代码如下：

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
const int Maxn = 2e5 + 5;

struct Treap {
	int son[2], val, cnt, key, size;
}t[Maxn];

#define lp t[p].son[0]
#define rp t[p].son[1]

int tot, root;//树的总节点数，用于传参的一个变量（同线段树合并） 

void update(int p) {//更新子树节点个数 
	t[p].size = t[lp].size + t[rp].size + t[p].cnt;
}

void rotate(int &p, int d) {//d为方向，1为左旋，0 为右旋 
	int tmp = t[p].son[d ^ 1];
	t[p].son[d ^ 1] = t[tmp].son[d];
	t[tmp].son[d] = p;
	update(p);
	update(tmp);
	p = tmp;//更新当前根节点 
}

void insert(int &p, int x) {
	if(!p) {//如果有可以直接放入的空位 
		p = ++tot;
		t[p].size = t[p].cnt = 1;
		t[p].val = x;
		t[p].key = rand();
		return ;
	}
	if(t[p].val == x) {//已有当前节点 
		t[p].cnt++;
		t[p].size++;
		return ;
	}
	int d = (x > t[p].val);
	insert(t[p].son[d], x);
	if(t[p].key > t[t[p].son[d]].key) {//不满足堆性质 
		rotate(p, d ^ 1);//旋转 
	}
	update(p);
}

void del(int &p, int x) {
	if(!p) return;//没有该节点 
	if(x < t[p].val) {
		del(lp, x);//查左子树 
	}
	else if(x > t[p].val) {
		del(rp, x);//查右子树 
	}
	else {//已经找到 
		if(!lp && !rp) {//叶子结点 
			t[p].cnt--;
			t[p].size--;
			if(t[p].cnt == 0) {
				p = 0;
			}
		}
		else if(lp && !rp) {//左子树不空 
			rotate(p, 1);//左旋
			del(rp, x);
		}
		else if(!lp && rp) {//右子树不空 
			rotate(p, 0);//右旋 
			del(lp, x);
		}
		else {
			int d = (t[lp].key < t[rp].key);
			rotate(p, d);//向优先级高的旋
			del(t[p].son[d], x); 
		}
	}
	update(p);
}

int ask(int p, int x) {
	if(!p) return 1;//空节点
	if(t[p].val == x) {//当前点权值等于 x 
		return t[lp].size + 1;
	} 
	else if(t[p].val < x) {//当前点权值小于 x 
		return ask(rp, x) + t[lp].size + t[p].cnt;
	}
	else {//当前点圈住大于 x 
		return ask(lp, x);
	}
} 

int find(int p, int x) {
	if(!p) return 0;//空节点
	if(t[lp].size >= x) {//当前点排名大于 x 
		return find(lp, x);
	} 
	else if(t[lp].size + t[p].cnt < x) {//当前点排名小于 x 
		return find(rp, x - t[lp].size - t[p].cnt);
	}
	else {//当前点排名就是 x 
		return t[p].val;
	}
}

int pre(int p, int x) {
	if(!p) return INT_MIN;//空节点
	if(t[p].val >= x) {//权值大于等于 x 
		return pre(lp, x);//搜索左子树 
	}
	else {
		return max(t[p].val, pre(rp, x));
	}
} 

int nxt(int p, int x) {
	if(!p) return INT_MAX;//空节点
	if(t[p].val <= x) {//权值小于等于 x  
		return nxt(rp, x);//搜索左子树 
	} 
	else {
		return min(t[p].val, nxt(lp, x));
	}
}

int n;

int main() {
	ios::sync_with_stdio(0);
	srand(time(0));
	cin >> n;
	while(n--) {
		int opt, x;
		cin >> opt >> x;
		switch(opt) {
			case 1: {
				insert(root, x);
				break;
			}
			case 2: {
				del(root, x);
				break;
			}
			case 3: {
				cout << ask(root, x) << '\n';
				break;
			}
			case 4: {
				cout << find(root, x) << '\n';
				break;
			}
			case 5: {
				cout << pre(root, x) << '\n';
				break;
			}
			case 6: {
				cout << nxt(root, x) << '\n';
				break;
			}
		}
	}
	return 0;
}

2.3 无旋 Treap

2.3.1 概述

无旋 Treap，最好写好调的平衡树，没有之一，可能唯一的缺点就是常数太大。

FHQ-Treap，又名无旋 Treap。

显然，FHQ-Treap 不使用旋转操作来维护平衡。他利用分裂和合并两个操作维护平衡，这种操作使得他天生具备可持久化、维护序列的特性。

2.3.2 分裂

分裂操作和两个参数有关，根节点 \(i\) 和关键值 \(key\)。

分裂操作分为按值分类和按排名分类两种，这里以按值分类为例。

分裂操作就是将一颗 Treap 按权值裁成小于等于 \(key\) 或者大于 \(key\) 的两颗 Treap。

重复递归分裂即可。

下面看代码。首先定义结构体：

struct FHQ_Treap {
	int l, r, val, key, size;
}t[Maxn];

接下来进行分裂操作：

void update(int p) {//更新子树节点数 
	t[p].size = t[lp].size + t[rp].size + 1;
}

void split(int p, int k, int &x, int &y) {
	//根节点，关键值，以及分裂后两个子树的根
	if(!p) {
		x = y = 0;
		return ;
	}
	if(t[p].val <= k) {//权值小于等于 k 
		x = p;//左子树全部属于第一个子树
		split(rp, k, rp, y); //分裂右子树 
	}
	else {//权值大于 x 
		y = p;//右子树全部属于第二个子树
		split(lp, k, x, lp);//分裂左子树 
	}
	update(p); 
}

2.3.3 合并

合并就是将两颗 Treap 合并成一颗 Treap。

由于此时两颗 Treap 中，一颗绝对严格小于另一颗。因此我们此时只需要维护堆的性质即可。

（在有旋 Treap 中，用旋转操作维护堆的性质。而在 FHQ-Treap 中，我们用合并操作维护堆的性质）

因此关键在于将谁作为谁的什么子树。

反复递归即可（其实和线段树合并的代码很像）。

int merge(int x, int y) {//返回合并后树根节点 
	if(!x || !y) {
		return x + y;
	}	
	if(t[x].key < t[y].key) {//x 的优先级小于 y 的优先级 
		t[x].r = merge(t[x].r, y);
		//将子树 y 并入子树 x 的右子树 
		update(x);
		return x; 
	}
	else {//x 的优先级大于 y 的优先级 
		t[y].l = merge(x, t[y].l);
		//将子树 x 并入子树 y 的左子树 
		update(y);
		return y;
	}
}

2.3.4 插入

假设要插入的数是 \(x\)，那么我们按 \(x\) 将 Treap 分裂成 \(a,b\) 两部分，将 \(x\) 与 \(a\) 合并，再与 \(b\) 合并即可。

2.3.5 删除

我们考虑先将小于等于 \(x\) 的部分与大于 \(x\) 的部分分离。对于第一部分，我们再将小于 \(x\) 和等于 \(x\) 的部分分离，最后中间等于 \(x\) 的部分删除即可。

2.3.6 查询

显然查询 \(a\) 的排名与在普通 BST 里没有什么区别。

至于求值、求前驱后继，与上面的分裂合并思想是一致的。

下面直接看完整代码。

2.3.7 完整代码

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
const int Maxn = 2e5 + 5;

struct FHQ_Treap {
	int l, r, val, key, size;
}t[Maxn];

int tot, root;
//节点数，传参变量 

#define lp t[p].l
#define rp t[p].r

void update(int p) {//更新子树节点数 
	t[p].size = t[lp].size + t[rp].size + 1;
}

void create(int &p, int x) {
	p = ++tot;
	t[p].val = x;
	t[p].key = rand();
	t[p].size = 1;
}

void split(int p, int k, int &x, int &y) {
	//根节点，关键值，以及分裂后两个子树的根
	if(!p) {
		x = y = 0;
		return ;
	}
	if(t[p].val <= k) {//权值小于等于 k 
		x = p;//左子树全部属于第一个子树
		split(rp, k, rp, y); //分裂右子树 
	}
	else {//权值大于 x 
		y = p;//右子树全部属于第二个子树
		split(lp, k, x, lp);//分裂左子树 
	}
	update(p); 
}

int merge(int x, int y) {//返回合并后树根节点 
	if(!x || !y) {
		return x + y;
	}	
	if(t[x].key < t[y].key) {//x 的优先级小于 y 的优先级 
		t[x].r = merge(t[x].r, y);
		//将子树 y 并入子树 x 的右子树 
		update(x);
		return x; 
	}
	else {//x 的优先级大于 y 的优先级 
		t[y].l = merge(x, t[y].l);
		//将子树 x 并入子树 y 的左子树 
		update(y);
		return y;
	}
}

int kth(int p, int k) {
	if(k == t[lp].size + 1) {//为当前点 
		return t[p].val;
	}
	if(k <= t[lp].size) {//在左子树中 
		return kth(lp, k);
	}
	else {//在右子树中 
		return kth(rp, k - t[lp].size - 1);
	}
}

int n;
int tmp;

int main() {
	srand(time(0));
	ios::sync_with_stdio(0);
	cin >> n;
	int now, x, y;//当前节点，分裂后树根 
	while(n--) {
		int opt, k;
		cin >> opt >> k;
		switch(opt) {
			case 1: {
				split(root, k, x, y);
				create(now, k);
				root = merge(merge(x, now), y);
				break;
			} 
			case 2: {
				split(root, k, x, tmp);
				split(x, k - 1, x, y);
				//分裂子树
				y = merge(t[y].l, t[y].r);
				//合并 x 的子树（也就是去掉 x）
				root = merge(merge(x, y), tmp);
				break;
			}
			case 3: {
				split(root, k - 1, x, y);//分离子树
				cout << t[x].size + 1 << '\n';//节点数量即为排名
				root = merge(x, y);
				break;
			}
			case 4: {
				cout << kth(root, k) << '\n';
				break;
			}
			case 5: {
				split(root, k - 1, x, y);
				cout << kth(x, t[x].size) << '\n';
				//x 的前驱也就是排名在 x 前一位的数，节点数量为 size
				root = merge(x, y); 
				break;
			}
			case 6: {
				split(root, k, x, y);
				cout << kth(y, 1) << '\n';
				//x 的后继也就是排名在 x 后一位的数，节点数量为 1 
				root = merge(x, y); 
				break;
			}
		}
	}
	return 0;
}

2.3.8 维护区间

一般来讲，平衡树用于维护权值，线段树用于维护区间。但既然线段树有权值线段树，那么平衡树自然也有区间平衡树。

2.3.8.1 建树

区间平衡树需要按下标建树。我们直接将新加入的点与原先的树合并即可。

建树完后，树的中序遍历为原数组。

2.3.8.2 分裂

上面我们提到过，分裂方式有两种：按值分裂和按排名分裂。现在维护区间的平衡树就要按排名分裂。

或者说，我们叫他按大小分裂。我们将 \(k\) 个点放在左树中，剩下的放在右树中。那么通过比较该节点 size 就可以判断分裂在那个子树。

2.3.8.3 区间翻转

首先我们容易发现（其实不容易），翻转一段区间在平衡树上的操作其实就是翻转每个点的左右儿子。

我们将整棵树按 \(r\) 分裂成两棵树，再将左边那棵树按 \(l-1\) 分裂。中间的那棵树就代表区间 \([l,r]\)。我们直接翻转中间的树即可。

但是我们发现，这样做的复杂度是假的。我们思考后发现，每一次翻转都不一定对之后的操作有影响。

因此，我们需要用到一个熟悉的东西——懒标记。

用懒标记记录是否要交换左右儿子，如果是就 pushdown 即可。

最后只要当经过节点的时候下放标记即可。

2.3.8.3 区间操作

其余的各种区间操作同样可以利用区间平衡树解决，例如区间加、区间乘、区间最值、区间平推等等。只需要维护对应的懒标记即可。

2.3.8.4 代码

P3391 【模板】文艺平衡树，区间翻转模板题。

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
const int Maxn = 2e5 + 5;

struct FHQ_Treap {
	int l, r, val, siz, key, tag;  
}t[Maxn];

int tot, root;

#define lp t[p].l
#define rp t[p].r

int create(int p) {///建立新节点
	t[++tot] = {0, 0, p, 1, rand(), 0};
	return tot;
}

void pushup(int p) {
	t[p].siz = t[lp].siz + t[rp].siz + 1;
}

void pushdown(int p) {//下放懒标记
	if(t[p].tag) {
		swap(lp, rp);
		t[lp].tag ^= 1;
		t[rp].tag ^= 1;
		t[p].tag = 0;
	}
}

void split(int p, int k, int &x, int &y) {//分裂
	if(!p) {
		x = y = 0;
		return ;
	}
	pushdown(p);
	if(k <= t[lp].siz) {
		y = p;
		split(lp, k, x, lp);
	}
	else {
		x = p;
		split(rp, k - t[lp].siz - 1, rp, y);
	}
	pushup(p);
}

int merge(int x, int y) {//合并
	if(!x || !y) {
		return x + y;
	}
	if(t[x].key < t[y].key) {
		pushdown(x);
		t[x].r = merge(t[x].r, y);
		pushup(x);
		return x;
	}
	else {
		pushdown(y);
		t[y].l = merge(x, t[y].l);
		pushup(y);
		return y;
	}
}

void print(int p) {//中序遍历输出
	if(!p) return;
	pushdown(p);
	print(lp);
	cout << t[p].val << " ";
	print(rp);
}

int n, m;

int main() {
	ios::sync_with_stdio(0);
	cin >> n >> m;
	for(int i = 1; i <= n; i++) {//下标建树
		root = merge(root, create(i));
	}
	while(m--) {
		int l, r;
		cin >> l >> r;
		int x, y, z;
		split(root, r, x, z);
		split(x, l - 1, x, y);//提取 [l,r] 区间
		t[y].tag ^= 1;//标记
		x = merge(x, y);
		root = merge(x, z);//合并回去
	}
	print(root);
	return 0;
}

（当然你也可以尝试使用平衡树去做线段树）

3 Splay

3.1 概述

Splay 树，又称伸展树，通过伸展操作不断将某个节点旋转至根节点，以此来维护平衡。在均摊 \(O(\log n)\) 的复杂度内完成插入、查找、删除操作。

3.2 基础 Splay

3.2.1 基本操作

首先定义 Splay 的结构体，与 Treap 的定义可以说是一模一样，但是多了一个父亲。

下面先实现三个操作。

pushup(p)：同 Treap，更新节点的 siz。
get(p) ：判断节点 \(p\) 是父亲的左儿子和右儿子。
clear(p)：销毁节点 \(p\)。

struct Splay {
	int fa, son[2], val, siz, cnt;
}t[Maxn];

#define lp (t[p].son[0])
#define rp (t[p].son[1])

int rt, tot;

void pushup(int p) {
	t[p].siz = t[lp].siz + t[rp].siz + t[p].cnt;
}

bool get(int p) {
	return p == t[t[p].fa].son[1];
}

void clear(int p) {
	t[p] = {0, 0, 0, 0, 0, 0};
}

3.2.2 旋转操作

Splay 树的旋转操作与 Treap 树的旋转操作基本一样，分为左旋和右旋，在此不再赘述。

注意还是略有不同，这里我们旋转的就是这个节点，而不是他的儿子。

void rotate(int p) {//下列讲解以右旋为例 
	int y = t[p].fa, z = t[y].fa, d = get(p);
	t[y].son[d] = t[p].son[d ^ 1]; // 将 y 的左儿子指向 p 的右儿子、
	if(t[p].son[d ^ 1]) t[t[p].son[d ^ 1]].fa = y;//p 的右儿子的父亲指向 y
	t[p].son[d ^ 1] = y;//将 p 的右儿子指向 y
	t[y].fa = p;//y 的父亲指向 p 
	t[p].fa = z;//p 的父亲指向 z
	if(z) t[z].son[y == t[z].son[1]] = p;//将 y 原本的位置给 p
	pushup(y);
	pushup(p); 
}

3.2.3 Splay 操作

Splay 树要求我们每操作一个节点，就要让该节点旋转至根节点。

一个简单的方法是，通过不断左旋右旋来达成目的。这被称作单旋。

然而单旋很容易被卡，因此一般不考虑。

这时候就需要双旋了。双旋的操作分为三种，首先定义 \(x\) 节点为当前节点，\(p\) 为 \(x\) 的父亲，\(g\) 为 \(p\) 的父亲。

\(zig\)：当 \(p\) 已经是根节点，即 \(x\) 为 \(p\) 的儿子时进行。此时直接将 \(x\) 进行对应旋转即可。
\(zig-zig\)：当 \(p\) 不为根节点，且 \(p\) 与父亲的相对位置和 \(x\) 与父亲的相对位置相同时进行。此时先旋转 \(p\) ，然后旋转 \(x\)。
\(zig-zag\)：当 \(p\) 不为根节点，且 \(p\) 与父亲的相对位置和 \(x\) 与父亲的相对位置不同时进行。此时将 \(x\) 旋转两次即可。

接下来放几张图，分别对应三个过程：

代码如下：

void splay(int p) {
	int f = t[p].fa;//父亲节点 
	while(f) {//不断旋转至根节点 
		if(t[f].fa) {
			rotate(get(p) == get(f) ? f : p);
			//zig-zig 和 zig-zag
			//区别就是旋转父亲还是当前节点 
		}
		rotate(p);
		//无论如何都要旋转当前节点 
		f = t[p].fa;
	}
	rt = p; 
}

3.2.4 插入

基本维护的操作结束后，就是其他操作了。

首先插入不是很难，与 Treap 类似，只需要注意进行 Splay 操作即可。

void insert(int k) {
	if(!rt) {//空树 
		t[++tot].val = k;//直接新建节点 
		t[tot].cnt++;
		rt = tot;
		pushup(rt);
		return ;
	}
	int p = rt, f = 0;
	while(1) {//模拟递归 
		if(t[p].val == k) {//已有当前节点 
			t[p].cnt++;
			pushup(p), pushup(f);
			splay(p);
			break;
		}
		f = p;
		p = t[p].son[t[p].val < k];//模拟递归查找过程
		//如果当前值小于 k 向右儿子查，否则向左儿子
		if(!p) {//找到且没有出现 
			t[++tot].val = k;
			t[tot].cnt++;
			t[tot].fa = f;
			t[f].son[t[f].val < k] = tot;//新建节点 
			pushup(tot), pushup(f);
			splay(tot);
			break;
		} 
	}
}

3.2.5 查询排名

显然直接按照定义查询即可。

int rnk(int k) {
	int res = 0, p = rt;
	while(1) {	
		if(k < t[p].val) {//向左子树寻找 
			p = lp;
		}
		else {//向右子树寻找 
			res += t[lp].siz;//累加答案 
			if(k == t[p].val) {//找到位置 
				splay(p);
				return res + 1; 
			}
			res += t[p].cnt;//注意累加当前节点次数 
			if(!rp) {
				if(p) splay(p);
				return res + 1;
			}
			p = rp;
		}
	}
}

3.2.6 查询值

依然按照定义查询。

int kth(int k) {
	int p = rt;
	while(1) {
		if(lp && k <= t[lp].siz) {//在左子树 
			p = lp;
		}
		else {//在右子树 
			k -= (t[lp].siz + t[p].cnt);//减掉左边的排名 
			if(k <= 0) {//在当前节点 
				splay(p);
				return t[p].val;
			}
			p = rp;
		}
	}
}

3.2.7 求前驱

首先我们插入 \(x\)，此时 \(x\) 就是根节点，然后他的前驱就是左子树中最靠右的节点。因此直接在左子树中不断找右儿子即可。

int pre() {
	int p = t[rt].son[0];//根节点（x）的左子树
	if(!p) return p;
	while(rp) p = rp;//不断找右儿子
	splay(p);
	return p;
}

3.2.8 求后继

与上面类似，为 \(x\) 的右子树中最靠左的节点。

int nxt() {
	int p = t[rt].son[1];//根节点（x）的右子树 
	if(!p) return p;
	while(lp) p = lp;//不断找左儿子 
	splay(p);
	return p;
}

3.2.9 删除

删除操作在 Splay 中同样有些复杂，我们先看一个前置芝士。

3.2.9.1 合并

我们设两棵树为 \(x,y\)（满足 \(x\) 每一个值小于 \(y\) 中的值），如果要合并两棵树，那么我们先将 \(x\) 树中的最大值旋到根节点，然后将 \(y\) 接到根节点的右子树即可。

3.2.9.2 删除

有了上面的前置，现在我们来看如何删除 Splay 的节点。

首先将 \(x\) 旋转到根节点，然后看 \(cnt\) 的数量。

如果有不止一个 \(x\)，那么将数量减一即可。
否则合并两颗左右子树即可。

代码如下：

void del(int k) {
	rnk(k);//随便搞一个操作让 k 旋转到根节点
	if(t[rt].cnt > 1) {
		t[rt].cnt--;
		pushup(rt);
		return;
	} 
	if(!t[rt].son[0] && !t[rt].son[1]) {//如果只有一个节点 
		clear(rt);//删除，变为空树 
		rt = 0;
		return ;
	}
	if(!t[rt].son[0]) {//只有右子树 
		int cur = rt;
		rt = t[rt].son[1];//根为右子树的根 
		t[rt].fa = 0;
		clear(cur);
		return ;
	} 
	if(!t[rt].son[1]) {//只有左子树 
		int cur = rt;
		rt = t[rt].son[0];
		t[rt].fa = 0;//根为左子树的根 
		clear(cur);
		return ;
	}
	//都有，需要合并 
	int cur = rt, x = pre();//此时根节点的前驱即为左子树中最大的数
	t[t[cur].son[1]].fa = x;
	t[x].son[1] = t[cur].son[1]; //右子树挂到左子树上
	clear(cur);
	pushup(rt);
	return ;
}

3.2.10 完整代码

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
const int Maxn = 2e5 + 5;

struct Splay {
	int fa, son[2], val, siz, cnt;
}t[Maxn];

#define lp (t[p].son[0])
#define rp (t[p].son[1])

int rt, tot;

void pushup(int p) {
	t[p].siz = t[lp].siz + t[rp].siz + t[p].cnt;
}

bool get(int p) {
	return p == t[t[p].fa].son[1];
}

void clear(int p) {
	t[p] = {0, 0, 0, 0, 0, 0};
}

void rotate(int p) {//下列讲解以右旋为例 
	int y = t[p].fa, z = t[y].fa, d = get(p);
	t[y].son[d] = t[p].son[d ^ 1]; // 将 y 的左儿子指向 p 的右儿子、
	if(t[p].son[d ^ 1]) t[t[p].son[d ^ 1]].fa = y;//p 的右儿子的父亲指向 y
	t[p].son[d ^ 1] = y;//将 p 的右儿子指向 y
	t[y].fa = p;//y 的父亲指向 p 
	t[p].fa = z;//p 的父亲指向 z
	if(z) t[z].son[y == t[z].son[1]] = p;//将 y 原本的位置给 p
	pushup(y);
	pushup(p); 
}

void splay(int p) {
	int f = t[p].fa;//父亲节点 
	while(f) {//不断旋转至根节点 
		if(t[f].fa) {
			rotate(get(p) == get(f) ? f : p);
			//zig-zig 和 zig-zag
			//区别就是旋转父亲还是当前节点 
		}
		rotate(p);
		//无论如何都要旋转当前节点 
		f = t[p].fa;
	}
	rt = p; 
}

void insert(int k) {
	if(!rt) {//空树 
		t[++tot].val = k;//直接新建节点 
		t[tot].cnt++;
		rt = tot;
		pushup(rt);
		return ;
	}
	int p = rt, f = 0;
	while(1) {//模拟递归 
		if(t[p].val == k) {//已有当前节点 
			t[p].cnt++;
			pushup(p), pushup(f);
			splay(p);
			break;
		}
		f = p;
		p = t[p].son[t[p].val < k];//模拟递归查找过程
		//如果当前值小于 k 向右儿子查，否则向左儿子
		if(!p) {//找到且没有出现 
			t[++tot].val = k;
			t[tot].cnt++;
			t[tot].fa = f;
			t[f].son[t[f].val < k] = tot;//新建节点 
			pushup(tot), pushup(f);
			splay(tot);
			break;
		} 
	}
}

int rnk(int k) {
	int res = 0, p = rt;
	while(1) {	
		if(k < t[p].val) {//向左子树寻找 
			p = lp;
		}
		else {//向右子树寻找 
			res += t[lp].siz;//累加答案 
			if(k == t[p].val) {//找到位置 
				splay(p);
				return res + 1; 
			}
			res += t[p].cnt;//注意累加当前节点次数 
			if(!rp) {
				if(p) splay(p);
				return res + 1;
			}
			p = rp;
		}
	}
}

int kth(int k) {
	int p = rt;
	while(1) {
		if(lp && k <= t[lp].siz) {//在左子树 
			p = lp;
		}
		else {//在右子树 
			k -= (t[lp].siz + t[p].cnt);//减掉左边的排名 
			if(k <= 0) {//在当前节点 
				splay(p);
				return t[p].val;
			}
			p = rp;
		}
	}
}

int pre() {
	int p = t[rt].son[0];//根节点（x）的左子树
	if(!p) return p;
	while(rp) p = rp;//不断找右儿子
	splay(p);
	return p;
}

int nxt() {
	int p = t[rt].son[1];//根节点（x）的右子树 
	if(!p) return p;
	while(lp) p = lp;//不断找左儿子 
	splay(p);
	return p;
}

void del(int k) {
	rnk(k);//随便搞一个操作让 k 旋转到根节点
	if(t[rt].cnt > 1) {
		t[rt].cnt--;
		pushup(rt);
		return;
	} 
	if(!t[rt].son[0] && !t[rt].son[1]) {//如果只有一个节点 
		clear(rt);//删除，变为空树 
		rt = 0;
		return ;
	}
	if(!t[rt].son[0]) {//只有右子树 
		int cur = rt;
		rt = t[rt].son[1];//根为右子树的根 
		t[rt].fa = 0;
		clear(cur);
		return ;
	} 
	if(!t[rt].son[1]) {//只有左子树 
		int cur = rt;
		rt = t[rt].son[0];
		t[rt].fa = 0;//根为左子树的根 
		clear(cur);
		return ;
	}
	//都有，需要合并 
	int cur = rt, x = pre();//此时根节点的前驱即为左子树中最大的数
	t[t[cur].son[1]].fa = x;
	t[x].son[1] = t[cur].son[1]; //右子树挂到左子树上
	clear(cur);
	pushup(rt);
	return ;
}

int n;

int main() {
	ios::sync_with_stdio(0);
	cin >> n;
	while(n--) {
		int opt, x;
		cin >> opt >> x;
		switch(opt) {
			case 1: {
				insert(x);
				break;
			}
			case 2: {
				del(x);
				break;
			}
			case 3: {
				cout << rnk(x) << '\n';
				break;
			}
			case 4: {
				cout << kth(x) << '\n';
				break;
			}
			case 5: {
				insert(x);
				cout << t[pre()].val << '\n';
				del(x);
				break;
			}
			case 6: {
				insert(x);
				cout << t[nxt()].val << '\n';
				del(x);
				break;
			}
		}
	}
	return 0;
}

3.2.11 维护区间

同 FHQ-Treap，Splay 也可以用于维护区间。

3.2.11.1 建树

我们模仿线段树的建树方式，递归建立区间 Splay 树。

int build(int l, int r, int f) {//返回编号 
	if(l > r) return 0;
	int mid = (l + r) >> 1, p = ++tot;
	t[p].val = a[mid], t[p].fa = f;//当前节点（为了满足中序遍历） 
	lp = build(l, mid - 1, p);
	rp = build(mid + 1, r, p);//递归建树 
	pushup(p);
	return p;
}

3.2.11.2 Splay 操作进阶

首先魔改一下 Splay 操作，我们加上一个值 v，表示要将 \(p\) 旋转至 \(v\) 的子树（\(v=0\) 时表示旋转至根节点）。

如下：

void splay(int p, int v) {
	int f = t[p].fa;
	while(f != v) { //区别只在于将 !=0 改成 != v
		if(t[f].fa != v) {
			rotate(get(p) == get(f) ? f : p);
		}
		rotate(p);
		f = t[p].fa;
	}
	if(v == 0) rt = p; 
}

3.2.11.3 区间翻转

假如翻转区间 \([l,r]\)，我们先将 \(l-1\) 翻到根节点：

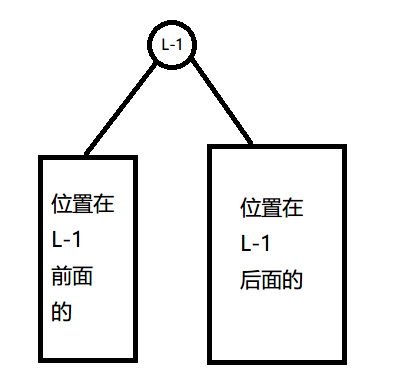
然后将 \(r+1\) 翻到 \(l-1\) 的下面：

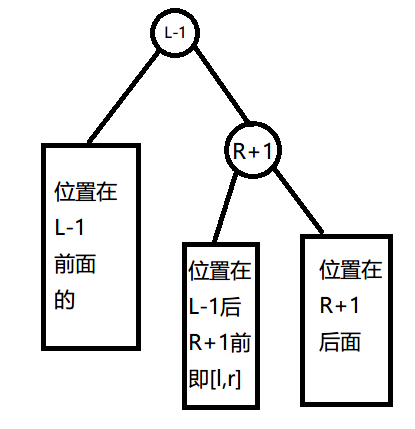
这样 \(r+1\) 的左子树就是区间 \([l,r]\)。

同时注意一个细节，由于我们可能会翻转区间 \([1,n]\)，因此实际建树时应当建 \([0,n+1]\)，那么此时查找 \(l-1,r+1\) 的位置就是查询排名为 \(l,r+2\) 的数。

同时利用懒标记维护即可，不再赘述。

3.2.11.4 代码

把各种函数魔改一下就行了。

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
const int Maxn = 2e5 + 5;

struct Splay {
	int fa, son[2], val, siz, tag;
}t[Maxn];

#define lp (t[p].son[0])
#define rp (t[p].son[1])

int rt, tot;

void pushup(int p) {
	t[p].siz = t[lp].siz + t[rp].siz + 1;
}

bool get(int p) {
	return p == t[t[p].fa].son[1];
}

void clear(int p) {
	t[p] = {0, 0, 0, 0, 0, 0};
}

void rotate(int p) {
	int y = t[p].fa, z = t[y].fa, d = get(p);
	t[y].son[d] = t[p].son[d ^ 1]; 
	if(t[p].son[d ^ 1]) t[t[p].son[d ^ 1]].fa = y;
	t[p].son[d ^ 1] = y;
	t[y].fa = p;
	t[p].fa = z;
	if(z) t[z].son[y == t[z].son[1]] = p;
	pushup(y);
	pushup(p); 
}

void splay(int p, int v) {
	int f = t[p].fa;
	while(f != v) {
		if(t[f].fa != v) {
			rotate(get(p) == get(f) ? f : p);
		}
		rotate(p);
		f = t[p].fa;
	}
	if(v == 0) rt = p; 
}

int build(int l, int r, int f) {//返回编号 
	if(l > r) return 0;
	int mid = (l + r) >> 1, p = ++tot;
	t[p].val = mid, t[p].fa = f;//当前节点（为了满足中序遍历） 
	lp = build(l, mid - 1, p);
	rp = build(mid + 1, r, p);//递归建树 
	pushup(p);
	return p;
}

void pushdown(int p) {
	if(t[p].tag) {
		swap(lp, rp);
		t[lp].tag ^= 1;
		t[rp].tag ^= 1;
		t[p].tag = 0;
	}
}

int kth(int k) {
	int p = rt;
	while(1) {
		pushdown(p);
		if(lp && k <= t[lp].siz) {//在左子树 
			p = lp;
		}
		else {//在右子树 
			k -= (t[lp].siz + 1);//减掉左边的排名 
			if(k <= 0) {//在当前节点 
				splay(p, 0);
				return p;//注意返回的是节点编号而非权值 
			}
			p = rp;
		}
	}
}

void reverse(int l, int r) {
	int x = kth(l), y = kth(r + 2);
	splay(x, 0), splay(y, x);
	int p = t[t[rt].son[1]].son[0];
	t[p].tag ^= 1;
}

int n, m;

void print(int p) {
	pushdown(p);
	if(lp) print(lp);
	if(t[p].val != 0 && t[p].val != n + 1) {
		cout << t[p].val << " ";
	}
	if(rp) print(rp);
}

int main() {
	ios::sync_with_stdio(0);
	cin >> n >> m;
	rt = build(0, n + 1, 0);
	while(m--) {
		int l, r;
		cin >> l >> r;
		reverse(l, r);
	}
	print(rt);
	return 0;
}

4 树套树

4.1 概述

树套树其实是一种思想，也就是外层一颗树，内层一棵树。

通常情况下，树套树的码量都极大（毕竟你要写两颗树）。同时，一般情况下，外层树是线段树或树状数组，内层树是线段树或平衡树。

在本章节中，只介绍线段树套平衡树这一数据结构。

4.2 实现

下面以 P3380 【模板】树套树为例，讲解线段树套平衡树的操作。

4.2.1 查询区间内排名

首先我们先找到区间在线段树上对应的节点，然后在每个节点中的平衡树中查询排名，然后把所有排名累加起来即可。

复杂度 \(O(\log^2 n)\)。

4.2.2 查询区间内值

显然这个操作是无法像操作 \(1\) 一样拆开了。所以我们考虑转化为判断这个数是不是排名为 \(k\) 的。显然这满足单调性，所以我们可以二分答案。

至于如何判断这个数的排名，建议去看 4.2.1。

复杂度 \(O(\log^3n)\)。

4.2.3 单点修改

找到这个点所对应的线段树上的节点，把这些节点的平衡树中的这个值修改即可。

复杂度 \(O(\log^2 n)\)。

4.2.4 求区间内前驱后继

这个操作是可以像操作 \(1\) 那样拆开的。找到区间对应的节点，利用平衡树求出前驱后继，然后对于所有区间取一个 \(\max\) 或 \(\min\) 即可。

复杂度 \(O(\log^2 n)\)。

4.2.5 代码

剩下的就是无休止的调代码了，总的时间复杂度大概是 \(O(n\log^3 n)\)。

注意：FHQ-Treap 常数过大，因此你要是写 FHQ 需要卡常。

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
const int Maxn = 5e4 + 5;
const int Inf = 2147483647;

int n, m, a[Maxn];

struct balanced_tree {
	struct FHQ_Treap {
		int l, r, val, siz, key;
	}t[Maxn * 50];
	int tot;
	inline void add(int &p, int k) {
		p = ++tot;
		t[p] = {0, 0, k, 1, rand()};
	}
	inline void pushup(int p) {
		t[p].siz = t[t[p].l].siz + t[t[p].r].siz + 1;
	}
	inline void split(int p, int k, int &x, int &y) {
		if(!p) {
			x = y = 0;
			return ;
		}
		if(t[p].val <= k) {
			x = p;
			split(t[p].r, k, t[p].r, y);
		}
		else {
			y = p;
			split(t[p].l, k, x, t[p].l);
		}
		pushup(p);
	}
	inline int merge(int x, int y) {
		if(!x || !y) {
			return x + y;
		}
		if(t[x].key < t[y].key) {
			t[x].r = merge(t[x].r, y);
			pushup(x);
			return x;
		}
		else {
			t[y].l = merge(x, t[y].l);
			pushup(y);
			return y;
		}
	}
	inline int kth(int p, int k) {
		if(t[t[p].l].siz + 1 == k) {
			return t[p].val;
		}
		if(k <= t[t[p].l].siz) {
			return kth(t[p].l, k);
		}
		else {
			return kth(t[p].r, k - t[t[p].l].siz - 1);
		}
	}
	inline int rnk(int &rt, int k) {
		int x, y, ans;
		split(rt, k - 1, x, y);
		ans = t[x].siz;
		rt = merge(x, y);
		return ans;
	}
	inline int pre(int &rt, int k) {
		int x, y, ans;
		split(rt, k - 1, x, y);
		if(t[x].siz) {
			ans = kth(x, t[x].siz);
		}
		else {
			ans = -Inf;
		}
		rt = merge(x, y);
		return ans;
	}
	inline int nxt(int &rt, int k) {
		int x, y, ans;
		split(rt, k, x, y);
		if(t[y].siz) {
			ans = kth(y, 1);
		}
		else{
			ans = Inf;
		}
		rt = merge(x, y);
		return ans;
	}
	inline void del(int &rt, int k) {
		int x, y, z;
		split(rt, k, x, z);
		split(x, k - 1, x, y);
		y = merge(t[y].l, t[y].r);
		rt = merge(merge(x, y), z);
	}
	inline void ins(int &rt, int k) {
		int x, y, now;
		if(!rt) {
			add(rt, k);
			return ;
		}
		split(rt, k, x, y);
		add(now, k);
		rt = merge(merge(x, now), y);
	}
}FHQ;

struct segment_tree {
	struct seg_tree {
		int l, r, rt;
	}t[Maxn << 2];	
	inline void build(int u, int l, int r) {
		t[u].l = l, t[u].r = r;
		for(int i = l; i <= r; i++) {
			FHQ.ins(t[u].rt, a[i]);
		}
		if(l == r) return ;
		int mid = (l + r) >> 1;
		build(u << 1, l, mid);
		build(u << 1 | 1, mid + 1, r);
	}
	inline int rnk(int u, int l, int r, int k) {
		if(t[u].l == l && t[u].r == r) {
			return FHQ.rnk(t[u].rt, k);
		}
		int mid = (t[u].l + t[u].r) >> 1;
		if(r <= mid) return rnk(u << 1, l, r, k);
		else if(l > mid) return rnk(u << 1 | 1, l, r, k);
		else return rnk(u << 1, l, mid, k) + rnk(u << 1 | 1, mid + 1, r, k);
	}
	inline int kth(int l, int r, int k) {
		int ll = 0, rr = 1e8 + 5, mid;
		while(ll < rr) {
			mid = (ll + rr + 1) >> 1;
			int p = rnk(1, l, r, mid); 
			if(p < k) {
				ll = mid;
			}
			else {
				rr = mid - 1;
			}
		}
		return rr;
	}
	inline void mdf(int u, int p, int k) {
		FHQ.del(t[u].rt, a[p]);
		FHQ.ins(t[u].rt, k);
		if(t[u].l == t[u].r) {
			return; 
		}
		int mid = (t[u].l + t[u].r) >> 1;
		if(p <= mid) mdf(u << 1, p, k);
		else mdf(u << 1 | 1, p, k);		
	}
	inline int pre(int u, int l, int r, int k) {
		if(t[u].l == l && t[u].r == r) {
			return FHQ.pre(t[u].rt, k);
		}
		int mid = (t[u].l + t[u].r) >> 1;
		if(r <= mid) return pre(u << 1, l, r, k);
		else if(l > mid) return pre(u << 1 | 1, l, r, k);
		else return max(pre(u << 1, l, mid, k), pre(u << 1 | 1, mid + 1, r, k));
	} 
	inline int nxt(int u, int l, int r, int k) {
		if(t[u].l == l && t[u].r == r) {
			return FHQ.nxt(t[u].rt, k);
		}
		int mid = (t[u].l + t[u].r) >> 1;
		if(r <= mid) return nxt(u << 1, l, r, k);
		else if(l > mid) return nxt(u << 1 | 1, l, r, k);
		else return min(nxt(u << 1, l, mid, k), nxt(u << 1 | 1, mid + 1, r, k));
	}
}SEG;

int main() {
	ios::sync_with_stdio(0);
	cin >> n >> m;
	for(int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	SEG.build(1, 1, n);
	while(m--) {
		int opt, x, y, z;
		cin >> opt >> x >> y;
		switch(opt) {
			case 1: {
				cin >> z;
				cout << SEG.rnk(1, x, y, z) + 1 << '\n';
				break;
			}
			case 2: {
				cin >> z;
				cout << SEG.kth(x, y, z) << '\n';
				break;
			}
			case 3: {
				SEG.mdf(1, x, y);
				a[x] = y;
				break;
			}
			case 4: {
				cin >> z;
				cout << SEG.pre(1, x, y, z) << '\n';
				break;
			}
			case 5: {
				cin >> z;
				cout << SEG.nxt(1, x, y, z) << '\n';
				break;
			}
		}	
	}
	return 0;
}

posted @ 2024-02-27 17:53 UKE_Automation 阅读(98) 评论(0) 收藏举报

刷新页面返回顶部

UKE_Automation

平衡树

1 二叉搜索树

1.1 定义

1.2 特性

2 Treap

2.1 概述

2.1.1 Treap 的性质

2.2 有旋 Treap

2.2.1 旋转

2.2.2 插入

2.2.3 删除

2.2.4 查询排名

2.2.5 查询值

2.2.6 求前驱

2.2.7 求后继

2.2.8 完整代码

2.3 无旋 Treap

2.3.1 概述

2.3.2 分裂

2.3.3 合并

2.3.4 插入

2.3.5 删除

2.3.6 查询

2.3.7 完整代码

2.3.8 维护区间

2.3.8.1 建树

2.3.8.2 分裂

2.3.8.3 区间翻转

2.3.8.3 区间操作

2.3.8.4 代码

3 Splay

3.1 概述

3.2 基础 Splay

3.2.1 基本操作

3.2.2 旋转操作

3.2.3 Splay 操作

3.2.4 插入

3.2.5 查询排名

3.2.6 查询值

3.2.7 求前驱

3.2.8 求后继

3.2.9 删除

3.2.9.1 合并

3.2.9.2 删除

3.2.10 完整代码

3.2.11 维护区间

3.2.11.1 建树

3.2.11.2 Splay 操作进阶

3.2.11.3 区间翻转

3.2.11.4 代码

4 树套树

4.1 概述

4.2 实现

4.2.1 查询区间内排名

4.2.2 查询区间内值

4.2.3 单点修改

4.2.4 求区间内前驱后继

4.2.5 代码

公告