「刷题记录 - 2020.07」
改成了上中下旬(好像不是均分?)分类,方便查找虽然我觉得我也刷不到那么多题。
2020.06.28~2020.07.10
loj - 3323:删自环(其实我也不知道数据里面有没有自环),点双分解。简单环贡献 \(\prod siz\),最多剩一个非简单环点双。这个点双大概长这样(画得好丑):
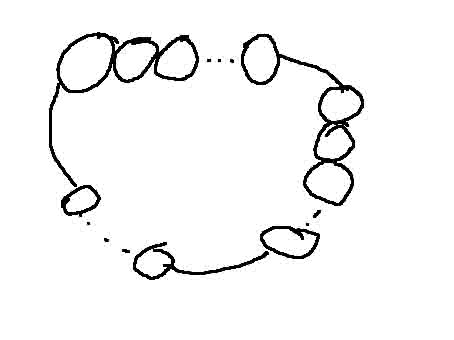
即环通过割点相接形成“糖葫芦”,“糖葫芦”再通过链相接。在这个点双内找任意三度点,check 一下 3 条边删掉是否变仙人掌,就可以还原出所有“糖葫芦”与链。之后分类讨论。
loj - 3324:记 \(f_k(n)\) 为 1 当且仅当先手必胜。不难猜测 \(f_k\) 具有分形结构,打表观察一下找到规律。然后写递归。
注意到这其实就是 \(fibnacci\) 博弈的推广情形,所以有更优美的做法。关于该做法及其证明需要依赖齐肯多夫表示法(即把数 \(n\) 分解成若干不相邻 \(fibnacci\) 数之和),这里有一篇详细的题解(懒癌.jpg)。
loj - 3325:直接暴力,期望得分100分。segment tree beats + 闵可夫斯基和合并凸包/神仙EI所介绍的线段树做法。两种做法都不想写,咕了。
泰勒展开 \(\ln(1-x^i) = -\sum\frac{x^{ij}}{j}\),然后就做完了。
首先你得去隔壁学点双怎么计数。设大小为 i 的点双有 \(a_i\) 个,直接对圆方树计数:
\(F(x)\) 是圆点,\(H(x)\) 是方点。最后答案为 \(F(x)[x^n]\),拉格朗日反演即可。
(顺便,恋恋的蔷薇绞肉机好难。打dldex已经有三次卡蔷薇了。心态炸裂,九字切都快99+了还是混不过qaq)
codeforces - 1264D2:等价于计算形如 "((...())...)" 作为子序列出现的串数量(同一串多次出现只算一次)。
设 \(a_i, s_i\) 分别表示前缀 i 中 '(' 数量与 '?' 数量。同理设 \(b_i, t_i\) 分别表示后缀 i 中 ')' 与 '?'。
枚举子序列最后一个 '(' 的出现位置 \(i\),枚举前面 '? -> (' 数量 \(x\) 与后面 '? -> )' 数量 y。则:
注意到 \(s_{i-1} + t_{i+1}\) 只有两种取值,于是可以 \(O(n)\) 做。
cf - 1081G:如果 \(p_x > p_{x+i} (1 \leq i \leq k)\),则 \(p_{x\dots x+k}\) 在之后的归并中不会分开。
考虑题目所给伪代码,它将原排列划分成若干块。
块内的逆序对可以直接根据期望线性性质得到 \(\frac{1}{2}\times\binom{siz}{2}\),考虑块与块之间:
设一个块的第 \(i\) 个元素 \(y\) \(>\) 另一个块的第 \(j\) 个元素 \(q\);再设 \(y\) 之前的块内最大值为 \(x\),\(q\) 之前的块内最大值为 \(p\)。
则 \((y, q)\) 形成逆序等价于 \(q < y \leq x < p\)(注意 \(x\) 可以等于 \(y\))。根据一开始所说的性质即可证明。
转化一下变成求 “\(q < y \leq x\)” 的方案减去 “\(q<y\leq x\) 且 \(q\) 之前的所有值 \(<x\)”。
以大小关系建拓扑图,发现是棵树,因此变成树的拓扑序这个经典问题,优化一下可以做到 \(O(n)\)。
外层还要枚举块的种类,不过由于每次都是均分所以块的大小几乎等大,种类为常数个。
loj - 3080:主元法的应用,取前 2 行 + 前 1 列做主元,详见《浅谈图模型上的随机游走问题 王修涵》
gym - 102586I:首先 \(N = 2\) 无解。
考虑构造 \(M\) 个置换,其中第 \(j\) 个为 \(i -> i+2^j\bmod N\)。
每个置换的作用可以等效地认为是 \(\pm 2^j\)。
所有置换的作用可以等效地认为是 \(\pm x\),其中 \(x\) 为奇数且在 \((0, 2^M)\) 中。
当 \(N\) 为奇数时,直接构造 \(K+1\) 个如上的置换即可。
当 \(N\) 为偶数时,构造 \(K - 1\) 个如上置换,然后考虑如何合并奇偶:
考虑循环 \((x,x+2,x+1,x+3)\),如果可以凑出 \(x,x+2\) 就可以凑出 \(x,x+1,x+2,x+3\)。
那么如果 \(N = 4k\),直接构造 \(k\) 个如上的循环就可以合并就奇偶;
否则先构造 \(k-1\) 个如上的循环合并前 \(N-2\) 个,再随便构造一个置换即可。
gym - 102586E:快被自己蠢哭了。。。
设 \(A_i\) 个数为 \(p_i\)(\(\sum p_i=N,\sum p_iA_i=S\)),则排列顺序有 \(\frac{N!}{\prod p_i!}\) 种。
在模 2 意义下这个式子不为 0 当且仅当二进制下 \(\sum p_i =N\) 不进位。
因此问题等价于求 \(\sum_{2^i\in N}2^ix_i = S,x_i\in A\) 的方案数。
背包不是np问题吗。
可以考虑做类数位 dp 的过程,从最低位起匹配 \(S\)。状态 \(dp(i, j)\) 表示匹配完前 \(i\) 位,现在是 \(2^i\times j\)。这样总共用到 \(O(MAXA\log N)\) 个状态,因此可以直接背包。
bitset 优化一下可以做到 \(O(K\frac{MAXA}{\omega}\log N)\)。
loj - 6181:答案等于 “无平方因子数 - 2*质数个数”。质数个数 \(O(\frac{n^{\frac{3}{4}}}{\log n})\) 做,无平方因子数可以枚举最大平方因子然后反演做到 \(O(\sqrt{n})\) 不过考虑到复杂度瓶颈不在这所以直接min-25也能过。
loj - 528:反演得到 \(\sum_p\lfloor\frac{N}{p}\rfloor\lfloor\frac{M}{p}\rfloor\sum_{d|p}\mu^2(d)\mu(\frac{p}{d})\),然后推导一下得到 \(\sum_{d|p}\mu^2(d)\mu(\frac{p}{d}) = [\exist x,p = x^2]\mu(x)\)。
loj - 6244:二项式反演变成 “钦定 i 个位置填对” 的方案数,它等于 \(\binom{k}{i}(n-i)^{\underline{k-i}}\)。
loj - 6160:红蓝边分别形成匹配,且无交集。
设 \(f_n\) 表示 \(2n\) 个点的完全二分图所形成的匹配数量(不一定是最大匹配),枚举交集容斥得到 \(\sum_{i=0}^{n}\binom{n}{i}n^{\underline{i}}\times f^2_{n-i}\)。
考虑怎么求 \(f\),有递推式 \(f_n = 2nf_{n-1}-(n-1)^2f_{n-2}\)。
含义为 “X 部 1 号点存在于匹配的方案数” + “Y 部 1 号点存在于匹配的方案数” - “两边 1 号点同时存在于匹配的方案数”。
然而我当时想的垃圾做法是:\(f_n\) 等价于把 \(n\) 个数划分成若干圆排列/排列的方案数。然后枚举 1 所在圆排列/排列得到递推式:
优化一下就变成 \(O(n)\)。虽然感觉可以再整式递推得到上面的递推式。
codeforces - 997C:考虑计算所有行列都颜色不同的方案数。设 \(f_i\) 表示在所有行颜色互不相同的前提下钦定 \(i\) 列颜色相同的方案数,容斥得到 \(\sum_{i=0}^{n}(-1)^i\binom{n}{i}f_i\)。
loj - 572:记 \(S_k(n) = \sum_{i=1}^{n}f^k(n)\),则原式为 \(\sum_{i=1}^{n}2\phi(i)S_k(\lfloor\frac{n}{i}\rfloor)-S_k(n)\),求出 \(S_k(\lfloor\frac{n}{i}\rfloor)\) 直接杜教筛 \(\sum\phi(i)\) 即可。
考虑每一个 \(prime^k_i\) 的贡献,记 \(g_i(n)\) 表示 \(\leq n\) 中只包含 \(\leq prime_i\) 的质因子的数量,则贡献可以通过 \(g_i(m)\) 与 \(\pi(\lfloor\frac{n}{m\times prime_i}\rfloor)-i+1\) 表示。
发现我们 min-25 筛实际上就是在枚举前半部分,只需要处理出 \(\pi(n)\) 就可以求出单个答案。使用 unordered_map 记忆化(虽然不用记忆化貌似也能莽过去)求出所有 \(S_k(\lfloor\frac{n}{i}\rfloor)\)。
不过我是直接递推出 \(g_i(n)\) 然后整除分块来做的,虽然过了但是分析不出复杂度,感觉像暴力剪枝。
loj - 2476:直接反演得到:
其中 \(sA_i = \sum_{i|d}A_d, tD_i = \sum_{d|i}\mu(\frac{i}{d})D_{d}\),剩下的同理。
注意到该式子有贡献当且仅当 \(lcm(i,j),lcm(i,k),lcm(j,k)\leq n\),建图然后上裸的三元环计数即可。理论时间复杂度 \(O(n\log n\sqrt{n\log n})\) 不过图并非针对性构造所以卡不满。当然要选择对 cache 友好的 vector 存图。
当然有更科学的解法。
大概就是对原式只反演两个 gcd,然后得到一个含 lcm 和 gcd 的式子,接下来先反演 lcm 并枚举 lcm 的参量,再反演 gcd。
gym - 102512C:记 \(c(N, X, Y) = \sum_{X+Y+2(i+j)=N}\frac{N!}{i!(X+i)!j!(Y+j)!}\) 表示走 \(N\) 步从 \((0, 0)\) 走到 \((\pm X,\pm Y)\) 的方案数。
记 \(M=\frac{N-X-Y}{2}\),通过一些推导得到 \(c(N, X, Y) = \binom{N}{M}\times\binom{X+M+Y+M}{X+M}\)。
考虑用总方案数 \(4^N\) 减去不合法方案数。
记 \(g(i,j)\) 表示走 \(i\) 步恰好在第 \(i\) 步走到第一次走到不合法点,且该点为第 \(j\) 个不合法的点的方案数(我们只考虑 \(|X| + |Y| = D\) 的 \((X, Y)\),这样只会有 \(O(D)\) 个不合法点)。
我们即是求 \(4^N-\sum_{i=1}^{N}4^{N-i}\sum_{j} g(i,j)\)。
再记 \(f(i,j)\) 表示走 \(i\) 步,终点为第 \(j\) 个不合法点的方案数,再记 \(h(i,j,k)\) 表示走 \(i\) 步,起点为 \(j\) 个不合法点,重点为第 \(k\) 个不合法点的方案数。
这两个都可以用我们一开始的方法算。
那么 \(f(n, x) = \sum_{i=1}^{n}\sum_{y}g(i,y)\times h(n-i,y,x)\)。\(O(N^2D^2)\) 递推算出 \(g\) 即可。
loj - 6158:冷静分析一下发现是求 lcp,写个 Z-algorithm 即可。注意还要讨论进位的问题。为什么线性算法跑不过二分+hash啊。
codeforces - 653F:建后缀自动机求每个后缀新贡献的子串。求合法子串可以用栈找到最后一个合法左括号,预处理出同层左括号即可做到线性不过因为太懒就写了棵线段树。
codeforces - 610E:维护同色段以及相邻同色段的信息,查询 \(O(k^2)\) 查。去隔壁珂朵莉树学习了一下同色段怎么比较好的维护。
codeforces - 741E:缝合题。比较两个选择的优劣可以后缀数组,注意要把每种选择的 rank 存储下来优化常数。后半部分分类讨论 \(k<B\) 与 \(k\geq B\) 处理可以做到 \(O(n\sqrt{n\log n})\)(当然如果你要用线性rmq就是 \(O(n\sqrt{n})\) 的)。
codeforces - 914F:显然这道题用bitset可以过。
查询串总长一定,则越长的串出现次数越少。考虑对原串分块,块大小为 \(B\),如果 \(>B\) 直接暴力匹配;否则分两类,块内的建后缀自动机查,跨块的暴力。
查询串总长与原串长等阶。前边部分 \(O(n\frac{n}{B})\);后半部分 \(O(n(\frac{n}{B} + B))\)。取 \(B = \sqrt{n}\) 最优为 \(O(n\sqrt{n})\)。
submission(bitset)。不想写分块,bitset多好啊。
loj - 3298:后缀数组搞出每个后缀与 T 的 LCS。查询时先找到 p >= l, p + lcs[p] >= r 的最小 p,再查 rmq(l, p - 1) 即可。
loj - 517:维护出每一位为 1 的个数再相加,排过序的和没排序的分开处理。
没排序的维护前缀和,排序的维护 trie。在求出每一位为 1 的个数之后,利用全局 xor 标记求出每一位异或出来为 1 的个数。
排序操作将没排序的插进 trie 中,然后给 trie 打异或标记(trie 异或标记对应交换子树标记),并清掉全局 xor 标记。
时空复杂度都是 \(O(n\log^2n)\) 闭眼提交就能过。
loj - 6537:均匀分布的话不难想到哈希,但是直接单模数哈希显然会碰撞,于是考虑选 10~20 个模数。
问题又在于怎么校验一个哈希值是否由一个数生成。我们对于每个数 x 生成校验码 x*MOD + C,其中 MOD 是大质数,校验码也拿去异或。
如果最终哈希值 h 满足 h*MOD + C 等于校验码异或和,则认为它是一个数生成的。
codeforces - 963D:关键在于每个串互不相同且串总长为 \(O(n)\)。每种长度的串 end-pos 并集为 \(O(n)\),最多有 \(O(\sqrt{n})\) 种不同长度,因此总的 end-pos 并集为 \(O(n\sqrt{n})\)。之后随便做即可。
loj - 2999:员工的进出时刻将 [0, M] 划分成若干段。没有钥匙的员工对应的限制:出发时刻往右的段必须开门;返回时刻往左的段必须开门。因此每段的贡献只取决于段的左右端点。
如果段同时需要 x, y 有钥匙才能开门,则 x, y 之间连边。最后得到若干条链,背包即可。时间复杂度 \(O(n^2)\)。
loj - 3034:可以转化成网格图左上角到右下角的最长路径。设 \(f_{i,j}\) 表示达到第 \(i\) 行第 \(j\) 列的最长路,以列递推,应有 \(f_{i,j} \geq f_{k,j}+(s_{i,j}-s_{k,j})\),即 \(f_{i,j}-s_{i,j}\geq f_{k,j}-s_{k,j}\)。
于是考虑维护 \(f_{i,j} - s_{i,j}\),从上一列来要对 \(f_{i,j}\) 前缀加;有的行变不合法了要对 \(s_{k,j}\) 后缀加(可以转成前缀加)。
将所有前缀加操作处理完后再从后往前线段树二分 + cover 维护单调性即可。可以发现总操作数为 \(O(n)\),因此时间复杂度 \(O(n\log n)\)。
显然有更优的模型转化。
loj - 6355:\(f(x, y) = \max\{f(i,j)-(a_x-a_i)^2-(b_y-b_j)^2\}+C_{x,y}\)。
优化一下,变成分两步决策:\(\begin{cases}f(x, y) = \max\{g(i,y)-(a_x-a_i)^2\}+C_{x,y} \\ g(i,y)=\max\{f(i,j)-(b_y-b_j)^2\}\end{cases}\)
拆开变斜率优化,不过由于在树上所以均摊复杂度不成立。
查询显然二分,修改时二分找弹掉的后缀,可以看成移动栈顶指针 + 单点修改。
时间复杂度 \(O(n^2\log n)\)。
codeforces - 917C:状压 + 矩阵幂。
codeforces - 232E:网格图经典分治,不过数据范围比较小,不需要使用 ZJOI2016 那题的取 min(n, m) 操作,直接对 m 分治。使用 bitset 可以做到 \(O((nm\log m + q)\frac{m}{\omega})\)
codeforces - 1168D:首先叶子等深度。找充要条件,如果对于每个结点 \(x\) 记 \(f_{c,x}\) 表示 \(x\) 到叶子的路径上 \(c\) 最大出现次数,则 \(\sum f_{c,x}\leq dep_{leaf}-dep_x\)。
必要性显然,充分性考虑强命题:我们可以拼出满足 \(g_{c,s}\geq f_{c,x}\) 的所有字符串 \(s\),其中 \(g_{c,s}\) 表示 \(c\) 在 \(s\) 中的出现次数。归纳即可。
然后裸的ddp 注意到二叉树条件并没有用到。我们考虑缩链,由于叶子等深度,所以缩链后二叉树高为 \(O(\sqrt{n})\)。暴力跳即可。
codeforces - 1185G2:因为 \(T\) 很大,考虑单物品逐个加入背包避免 \(O(T^2)\) 的时间复杂度。
记 \(h_{x,y,z}\) 表示 A 类物品 \(x\) 个,B 类物品 \(y\) 个,交叉着放形成 \(z\) 个段的方案数。可以 \(O(n^4)\) 预处理。
记 \(f_{x,y,t}\) 表示 A 类物品 \(x\) 个,B 类物品 \(y\) 个,物品体积为 \(t\) 的方案数;记 \(p_{x,t}\) 表示物品 \(x\) 个,体积为 \(t\) 的方案数。
新加入一类物品时,先 \(p_{x,t}\to f_{x,0,t}\),再 \(O(n^3T)\) 求出 \(f_{x,y,t}\),再 \(O(n^3T)\) 把 \(f_{x,y,t} \to p_{z,t}\)(需要 \(h_{x,y,z}\))。
loj - 2737:单环输出 0。否则求基环树森林中最大点不相交路径权值和,断环成树然后 dp 即可。
atcoder - AGC017E:积木为有向边,左积木接地为白点,右积木接地为黑点。则相当于判定“是否存在若干条白点到黑点的欧拉路径(注意不能是欧拉回路),路径的无交并为边集”。
对于每个不是单点的连通块,白点入边 \(\leq\) 出边,黑点入边 \(\geq\) 出边,入边总数 = 出边总数。且至少存在一个白点满足入边 $\not = $ 出边。
2020.07.11~2020.07.20
codeforces - 903G:最大流转最小鸽,区间加 + 维护最小值。
loj - 6199/luogu - P4688:莫队 + bitset。
由于元素总和一定,离散化时给每种元素预留位置即可做可重集取交集。
可以分组做莫队优化空间。由于时间瓶颈在 bitset 而不在莫队所以没有问题。
submission(loj)。
submission(luogu),改进了一些常数。
codeforces - 1129D:dp + 分块优化。每个块内的权值是连续的 \(O(\sqrt{n})\) 个,所以重构复杂度可以做到 \(O(\sqrt{n})\)。
loj - 2537:dp + 线段树合并优化。加强版(ZJOI2019的那道题,没有二叉树限制)需要 ddp。
codeforces - 1260F:从小到大扫描每种合法的 \(h\),点分树动态维护一下贡献。时间复杂度 \(O(maxh + n\log n)\)(离散化过后应该可以 \(O(n\log n)\))。
loj - 558:lct 维护子树信息。为了在 makeroot 的时候快速维护黑点到根的距离和,可以另外维护 reverse 之后的 sum',reverse 时将 sum 与维护的 sum' 交换即可。
loj - 6515:离线显然线段树分治,讲讲在线做法:
维护两个栈与两个 dp。这里把中途 dp 状态存下来,退栈时只需要移动栈顶指针即可。查询时单调队列可以 \(O(p)\) 查。
问题主要在于某个栈为空时,这个时候暴力把另一个栈重构成大小相等的两个栈即可。这部分势能分析一下是 \(O(mp)\) 的。因此总时间复杂度 \(O(mp)\)。
nowcoder - 5667I:发现是隐式平面图最小割,转对偶图最短路。(自己没做出来,被初中的小朋友切出来了,感觉自己退役感++)
代码懒得写了,只是怕自己又忘记了,所以记录一下。
uoj - 46:离线做法 \(O(n\log n)\) 很简单。直接在线有个显然的树套树做法,但是空间开不下。
考虑在线两个套路:根号分治与二进制分组。根号分治据说可以分块套分块搞出来。
考虑二进制分组。发现可以把这个过程解构成线段树,每次在最后加入叶子并一路合并上去。只要保证结点信息和结点大小有关即可确保复杂度。
结点内共有 \(x\) 种标记,将原序列分成最多 \(2x+1\) 段。因此只需要维护每一段的端点以及对应的标记即可,这样结点信息是 \(O(size)\) 的。
合并时使用类归并的过程可以做到线性,因此这部分的复杂度 \(O(m\log m)\),其中 \(m\) 是修改次数。
查询时定义线段树上结点,结点内二分即可。一次查询复杂度 \(O(\log^2)\)。
loj - 6609:\(n\) 行中每一行必须放满两颗。如果允许一行的两颗石头放在相同列,则转化成 \(2n\) 个数的序列问题。
因此考虑容斥。枚举 \(i\) 行强制放同一列,剩下有 \(j\) 列放了 \(2\) 个,有 \(k\) 列放了 \(1\) 个:
卷积即可。
codeforces - 1195F:用相邻点之间的向量表示凸多边形。求闵可夫斯基和时,新凸包上的向量可以由原凸包上的向量按一定顺序拼接得到。
那岂不是区间凸包的点数求和 注意到三点共线并不能算,所以我们需要去掉重复的向量。因此转化成区间颜色种类数,莫队即可。
(如果要得到新凸包,可以先求出最左下的点之和,它一定在新凸包上。然后two-points 即可。然后你就可以去做ynoi的第六分块了)
codeforces - 77E:处理多圆问题,不难想到使用圆反演。
考虑圆反演的应用中,大多是把过反演中心的圆变成直线。因此我们以黑黄圆切点为反演中心,以黄圆直径为反演半径作圆反演。
这样绿圆与粉圆就变成了夹在平行直线间的圆,直接算即可。需要注意圆心反演过去不一定是圆心。
loj - 2549:若 \(\vec{dv}\) 不合法,则 \(\exist p_1\in V_1,p_2\in V_2,p_2+\vec{dv}=p_1\)。也即 \(\vec{dv}\in V_1 - V_2\),其中点集的加减为闵可夫斯基和。
因此做个凸包闵可夫斯基和,然后问题变成查询点是否在凸包内,离线扫描线即可。
update:查点在凸包内在线也可以做,二分即可。
codeforces - 1354G:如果找到一个 stone box,则通过倍增即可找到第一个 gift box。
我们尝试判断第一个 box 是否为 stone box,如果不是则显然它是答案。
注意到 \(k\leq \frac{n}{2}\) 且交互库并非针对性构造,因此随机抽取得到 stone box 的期望 \(\leq 2\)。我们随机抽取一个与第一个比较,假如第一个较小则它不是 stone box。
codeforces - 1372F:保证每种数均摊 4 次找到所在区间即可。
假如当前区间众数出现了 f 次,就将区间分为长度为 f 的若干段,然后每一段递归处理。为了保证每种数均摊 4 次,需要加入一些剪枝。具体看代码。
我怎么感觉我的做法每种数只均摊了3次啊。。。
codeforces - 1336D:考虑每次询问的结果与上一次差分,如果询问的 \(x > 1\),则 triplet 会告诉 \(a_x\) 的值;straight 会告诉 \(a_{x-2}a_{x-1}+a_{x-1}a_{x+1}+a_{x+1}a_{x+2}\) 的值。
先询问 \(1, 2, 3, 1\)。此时 \(a_1\) 显然已知;通过询问 \(2\) 得到 \((a_1 + 1)a_3+a_3a_4=a_3(a_1+a_4+1)\),可以知道 \(a_3\) 是否为 \(0\);通过第二次询问 \(1\) 得到 \((a_2 + 1)(a_3 + 1)\),解出 \(a_2\)。
对于 \(4 < i < n\),通过询问 \(i-1\) 已知 \((a_{i-3}+1)(a_{i-2}+1)+(a_{i-2}+1+a_{i+2})a_i\),也可以确定 \(a_i\) 是否为 \(0\),再询问 \(i\) 即可。
对于 \(i = n\),可以由询问 \(n - 1\) 得到 \((a_{n-3}+1)(a_{n-2}+1)+(a_{n-2}+1)a_n\),解出 \(a_n\)。总共恰好 \(n\) 次操作。
codechef - SUMDIS:若 \(u<i<v\),则 \(u\to v\) 的路径必然包含 \(i-1,i,i+1\) 中的某一个。
考虑分治,每次计算经过 \(mid-1,mid,mid+1\) 的最短路径。求三遍二维偏序即可得到分别经过 \(mid - 1, mid, mid + 1\) 的最短路径总长。
2020.07.21~2020.07.31
loj - 2569:子任务 1 显然暴力删去 mn 与 mx 可还原出序列。
子任务 2 可以鸽笼原理,最大距离 \(\geq \lceil\frac{mx-mn}{n} \rceil\),按这个大小分块,则最大距离必然跨块。依次查询每个块即可,小心被卡成 \(3N + 1\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号