有向图 Tarjan 求强连通分量详解
\(\text{Upd on 2025/11/26}\):部分内容重写。
好在没有 KMP 那么抽象。优化代码。
引入
给定一个 \(n\) 个点 \(m\) 条边有向图,每个点有一个权值,求一条路径,使路径经过的点权值之和最大。你只需要求出这个权值和。
允许多次经过一条边或者一个点,但是,重复经过的点,权值只计算一次。权值大于等于 \(0\)。
这明显需要考虑环,因为从环上任何一个节点进入环之后,整个环都可以被遍历到,肯定更优,并且能够去到更多的节点。
因此我们可以将所有 强连通分量 都变成一个节点来顶替其原来的位置,并重新建图,使原图成为一个有向无环图后求解。
有向图 Tarjan 求强连通分量
有向图下 DFS 生成树
我们需要先了解一下 DFS 生成树。
如图:
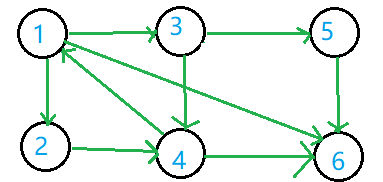
其可能的 DFS 生成树是:
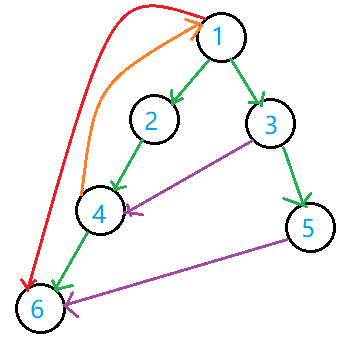
显然,这并不是一棵树。
边分为四种:
- 树边(如 \(1\sim 2\)):使用绿色标注,指向子节点。
- 回溯边(如 \(4\sim 1\)):使用橙色标注,又称返祖边、回边,指向祖先节点。
- 前向边(如 \(1\sim 6\)):使用红色标注,指向子节点的子树中的某一节点。
- 横边(如 \(3\sim 4\)):使用紫色标注,又称横叉边,指向当前节点某一祖先的另一子树中的节点。
Tarjan 算法流程
维护信息
在深搜的同时,维护 \(\textit{dfn}_i,\textit{low}_i\)、一个栈 \(s\) 和一个标记数组 \(\textit{in}\) 用于标记 \(i\) 是否位于栈 \(s\) 内。
\(\textit{dfn}_x\) 表示 \(x\) 的时间戳,即 DFS 序中第几个被搜索到的节点。
\(\textit{low}_x\) 表示 \(x\) 在 DFS 生成树中能够回退到的最早的位置(DFS 序),这个位置在求解 \(x\) 时需要在栈 \(s\) 中。
每当搜索到一个节点 \(x\) 时,就将其加入栈 \(s\),并标记 \(\textit{in}_x=\mathrm{true}\)。注意,栈 \(s\) 不是 DFS 搜索栈,不应当在递归结束前出栈。
更新信息
对于 \(\textit{dfn}_x,\textit{low}_x\),最初的初始值都是其时间戳。
\(\textit{low}_x\) 为其时间戳即表示其至少能够回退至自己。
遍历 \(x\) 的子节点 \(y\),若 \(\textit{dfn}_y=0\) 则代表还没有搜索过,进行搜索完成之后用 \(\textit{low}_y\) 来更新 \(\textit{low}_x\):
因为 \(x\) 有可能先走到子节点 \(y\),然后再从子节点通过回溯边走到更高(更早)的位置,因此需要更新。
但是若 \(\textit{dfn}_y\neq 0\),则代表已经搜索过,这时需要通过 \(\textit{in}\) 判断其是否在栈 \(s\) 中。
首先,\((x,y)\) 不可能是树边,因为 DFS 生成树显然是按照树边的顺序分配 \(\textit{dfn}\) 的。
-
如果在栈 \(s\) 中,代表 \(y\) 已经访问过,是 \(x\) 的祖先节点,则边 \((x,y)\) 是一条回溯边,更新答案:
\[low_x=\min(low_x,dfn_y) \] -
如果不是,则代表边 \((x,y)\) 是一条前向边或横边,不能够更新答案。
为什么不在栈 $s$ 中就是前向边或横边?
此处不是树边,原因见上文。
因为 $y$ 本来应该是 $x$ 的子节点,按照树边未曾被访问过,但是却已经被其他节点作为父节点访问过了(所以 $\textit{dfn}_y>0$),而又在栈中,代表 $y$ 其实是 $x$ 的祖先节点。即回溯边。
当通过子节点更新完成之后,如果仍然有 \(\textit{dfn}_x=\textit{low}_x\),则代表 \(x\) 是这个强连通分量在DFS 生成树上的根节点。
因为 \(\textit{dfn}_x=\textit{low}_x\) 代表 \(x\) 的子树中,没有路径能够使 \(x\) 走出去是条死路。
这时,我们再将栈 \(s\) 中 \(x\) 及在 \(x\) 之后加入栈的元素全部出栈,这些元素就是一个强连通分量。
参考代码
int dfn[N+1],id[N+1];//id[i]:i的强连通分量的编号
void Tarjan(int x){
static int cnt,low[N+1];
static bool in[N+1];
static vector<int>s;
dfn[x]=low[x]=++cnt;
in[x]=true;
s.push_back(x);
for(int i:old[x]){
if(!dfn[i]){
Tarjan(i);
low[x]=min(low[x],low[i]);
}else if(in[i]){
low[x]=min(low[x],dfn[i]);
}
}
if(dfn[x]==low[x]){
build.n++;
while(s.back()!=x){
in[s.back()]=false;
id[s.back()]=build.n;
s.pop_back();
}
in[s.back()]=false;
id[s.back()]=build.n;
s.pop_back();
}
}
//...
for(int i=1;i<=old.n;i++){
if(!dfn[i]){
Tarjan(i);
}
}
Tarjan 缩点
求出强连通分量之后,重新建图即可,注意避免自环。
void Build(){
for(int i=1;i<=old.n;i++){
//do something about nodes
for(int j:old[i]){
if(id[i]==id[j]){
continue;
}
//do something about edges
build[id[i]].push_back(id[j]);
}
}
}
例题 AC 代码
Tarjan 缩点后重新建图成为有向无环图,并且进行拓扑排序后即可 DP 求解。
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=1e4;
struct graph{
int n,a[N+1];
vector<int>g[N+1];
vector<int>& operator [](int x){
return g[x];
}
}old,build;
int dfn[N+1],id[N+1];
void Tarjan(int x){
static int cnt,low[N+1];
static bool in[N+1];
static vector<int>s;
dfn[x]=low[x]=++cnt;
in[x]=true;
s.push_back(x);
for(int i:old[x]){
if(!dfn[i]){
Tarjan(i);
low[x]=min(low[x],low[i]);
}else if(in[i]){
low[x]=min(low[x],dfn[i]);
}
}
if(dfn[x]==low[x]){
build.n++;
while(s.back()!=x){
in[s.back()]=false;
id[s.back()]=build.n;
s.pop_back();
}
in[s.back()]=false;
id[s.back()]=build.n;
s.pop_back();
}
}
void Build(){
for(int i=1;i<=old.n;i++){
build.a[id[i]]+=old.a[i];
for(int j:old[i]){
if(id[i]==id[j]){
continue;
}
build[id[i]].push_back(id[j]);
}
}
}
int order[N+1];
void topSort(){
static int in[N+1];
for(int i=1;i<=build.n;i++){
for(int j:build[i]){
in[j]++;
}
}
int front=1,rear=1;
for(int i=1;i<=build.n;i++){
if(!in[i]){
order[rear++]=i;
}
}
while(front<rear){
int x=order[front++];
for(int i:build[x]){
in[i]--;
if(!in[i]){
order[rear++]=i;
}
}
}
}
int Dp(){
topSort();
static int dp[N+1];
int ans=0;
for(int i=1;i<=build.n;i++){
int x=order[i];
dp[x]+=build.a[x];
ans=max(ans,dp[x]);
for(int v:build[x]){
dp[v]=max(dp[v],dp[x]);
}
}
return ans;
}
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int m;
cin>>old.n>>m;
for(int i=1;i<=old.n;i++){
cin>>old.a[i];
}
while(m--){
int u,v;
cin>>u>>v;
old[u].push_back(v);
}
for(int i=1;i<=old.n;i++){
if(!dfn[i]){
Tarjan(i);
}
}
Build();
cout<<Dp()<<'\n';
cout.flush();
/*fclose(stdin);
fclose(stdout);*/
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号