无向图 Tarjan 边双连通分量详解

例题链接

只有无向图有边双连通分量

有向图没有“边双连通分量”这个概念，只有“连通分量”、“强连通分量”和“弱连通分量”。

有向图见强连通分量。

边双连通分量

众所周知，在有向图中，存在强连通分量，强连通分量中的任意两点是连通的。

而在无向图中，同样存在边双连通分量。

边双连通

若一个无向连通图删去任意一条边之后仍然连通，则该图边双连通。

边双连通分量

在满足边双连通的前提下尽可能大的子图。

Tarjan 求边双连通分量

前置知识

Tarjan 求强连通分量。

---

其实把求有向图强连通分量的代码拿过来改改就行了，

无向图转有向图存储下环的误判

具体而言，就是不能出现如图的情况：

\(x,y\) 之间只有一条边，不是环，然而如果转换为有向图存储：

就存在了环。

因此我们需要防止其重复走，因此我们可以给边标号。

但是这样其实不是最优的，有一种更好的方式：邻接表存储边时，从 \(2\) 号开始存储，并且无向边转换为的两条有向边相邻存储。

这样的好处就是，比如说 \(x\) 号边是代表 \(u\to v\) 的，那么 \(x\oplus 1\) 号边代表的就是 \(v\to u\) 的，其中 \(\oplus\) 表示异或。

前向边与横边不存在

一棵有向图的 DFS 生成树如图：

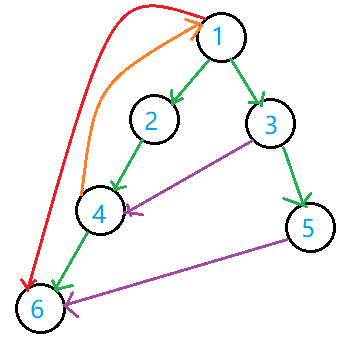
图中绿色为普通树边，橙色为回溯边，红色为前向边，紫色为横边。

考虑到无向图，实际上 DFS 生成树中只有普通树边和回溯边。

• 前向边不存在，因为无向，因此前向边反向就是一条回溯边。

• 横边不存在，因为按照 DFS 搜索顺序不会使其有可能存在。

  例如图中搜索到 \(4\) 之后，按照 DFS 的原则会先后搜索 \(3,6\)，不可能只搜索 \(6\) 然后回退至 \(1\) 再搜索到 \(3\)，然后连横边。

即化为：

也就是说，我们不再需要判断元素是否在栈中（判断了也能过），更新 \(\textit{low}_x\) 部分的代码可以简化为：

if(!dfn[g[i].v]){
    Tarjan(g[i].v,i);
    low[x]=min(low[x],low[g[i].v]);
}else{
    low[x]=min(low[x],dfn[g[i].v]);
}

答案存储

使用 vector 套 vector 维护即可。

vector<vector<int> >ans;

边双连通分量的判定

考虑对于一个点 \(x\)，若 \(\textit{dfn}_x=\textit{low}_x\)，代表 \(x\) 不能回退到祖先节点，则删去边 \((x,\textit{father}_x)\) 必然不连通，因此 \(x\) 和 \(\textit{father}_x\) 在两个边双连通分量中。

那么栈中所有 \(\textit{dfn}_i\geq\textit{dfn}_x\) 的节点就是 \(x\) 的子节点，同属于一个边双连通分量。从栈里一直出栈直到 \(x\)，即可找出该边双连通分量的所有结点。

AC 代码

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=5e5,M=2e6;
struct graph{
	int size,h[N+1];
	struct edge{
		int v,r;
	}e[(M<<1)+2];
	
	graph(){
		size=1;
	}
	
	void create(int u,int v){
		e[++size]={v,h[u]};
		h[u]=size;
	}
	
	edge& operator [](int x){
		return e[x];
	}
}g;
int n;
vector<vector<int>>ans;
int dfn[N+1];
void Tarjan(int x,int id){
	static int cnt,low[N+1];
	static vector<int>s;
	dfn[x]=low[x]=++cnt;
	s.push_back(x);
	for(int i=g.h[x];i;i=g[i].r){
		if((i^1)==id){
			continue;
		}
		if(!dfn[g[i].v]){
			Tarjan(g[i].v,i);
			low[x]=min(low[x],low[g[i].v]);
		}else{
			low[x]=min(low[x],dfn[g[i].v]);
		}
	}
	if(dfn[x]==low[x]){
		vector<int>pl;
		while(s.back()!=x){
			pl.push_back(s.back());
			s.pop_back();
		}
		pl.push_back(s.back());
		s.pop_back();
		ans.push_back(pl);
	}
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	
	int m;
	cin>>n>>m;
	while(m--){
		int u,v;
		cin>>u>>v;
		g.create(u,v);
		g.create(v,u);
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]){
			Tarjan(i,0);
		}
	}
	cout<<ans.size()<<'\n'; 
	for(auto &i:ans){
		cout<<i.size()<<' ';
		for(auto j:i){
			cout<<j<<' ';
		}
		cout<<'\n';
	}
	
	cout.flush();
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}