无向图 Tarjan 点双连通分量详解

例题链接

有向图没有点双连通分量

有向图请见强连通分量。

# 点双连通分量

点双连通

若一个无向连通图删去任意一个点之后仍然连通，则该图点双连通。

点双连通分量

在满足边双连通的前提下尽可能大的子图。

Tarjan 求点双连通分量

前置知识

Tarjan 求割点。

三条性质

• 两个点双连通分量存在至多一个公共点。

  证明

  假设两个点双连通分量可以存在至少两个公共点。

  

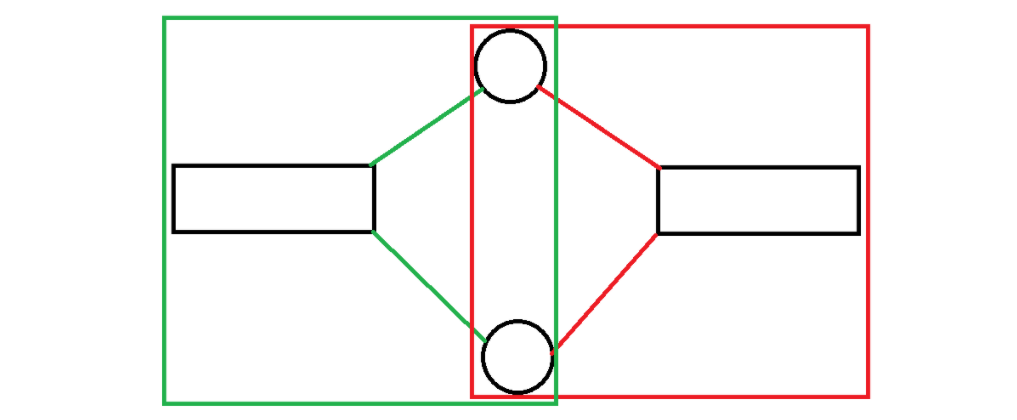
  如图中绿色点双连通分量和红色点双连通分量，显然将二者合并之后仍然满足点双连通分量的定义，因此二者都不是点双连通分量（不满足“极大”）。

  与假设矛盾，故原命题成立。

• 两个点双连通分量的公共点如果存在则一定是割点。

  证明

  假设两个点双连通分量存在的公共点不为割点。

  

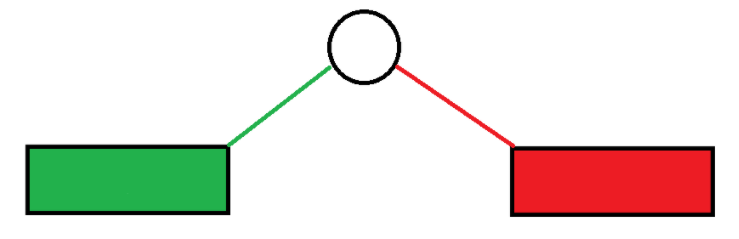
  则如图所示，由割点的性质，断开并不会导致不连通，因此绿色部分和红色部分也可以合并，因此绿色部分和红色部分都不为点双连通分量。

  与假设矛盾，故原命题成立。

• 点双连通分量内 \(\textit{dfn}\) 最小的节点一定是割点或 DFS 生成树的根节点。

  证明

  令某点双连通分量内 $\textit{dfn}$ 最小的节点为 $x$。

  1. 当 $x$ 为根节点时：

     显然成立。因为在 DFS 生成树中，深度最小的节点 $\textit{dfn}$ 最小，最小时可以显然为根节点。

  2. 当 $x$ 不为根节点时：

     假设节点 $x$ 不为割点。

     那么将该点双连通分量与 $x$ 的父节点合并到一起，显然可以成为一个点双连通分量，则 $x$ 不是 $\textit{dfn}$ 最小的节点。

     与假设矛盾，故此种情况下原命题成立。

  证毕。

分类讨论

分类讨论：

1. 当节点 \(x\) 为割点时，则点 \(x\) 一定是某个点双连通分量在 DFS 生成树上的根节点。
2. 当节点 \(x\) 为 DFS 生成树的根节点时：
   1. 子树不存在，则节点 \(x\) 是一个孤立点，视为一个点双连通分量（的根节点）。
   2. 存在一棵子树，则节点 \(x\) 是点双连通分量的根节点。
   3. 存在至少两棵子树，则节点 \(x\) 是割点（可以参考割点的判定），即某个点双连通分量在 DFS 生成树上的根节点。

总结一下就可以发现，点双连通分量一定在割点或根节点的子树中。

用一个栈维护节点，那么在找到割点或根节点时，将其子树内的点归到一个新的点双即可。

如何确保子树内的点一定属于这个点双连通分量

由 DFS 生成树和递归，递归至当前的 $x$ 时，$x$ 子树内可能会存在其他点双连通分量，但是这些点双连通分量已经出栈（暂不考虑割点和根节点），因此在求解 $x$ 时并不会影响到。

对于割点 $y$，如果在求解 $x$ 时在栈内，说明 $x,y$ 所在点双连通分量的公共节点是 $y$，$y$ 应当被出栈记录。

对于根节点，显然只会是栈底，且只有自己能够访问到，不影响答案的正确性。

注意这个点可能还是与其它点双的公共点，所以不能将其出栈，**只应当出栈到其子节点**。

点双连通分量的判定

如果说对于 \(x\) 能够到达的节点 \(i\)，有 \(\textit{low}_i\geq\textit{dfn}_x\)，则 \(i\) 及其子树均在 \(x\) 的子树内。那么栈中找出子树 \(i\) 即可。

同时还要特判孤立点。

例题 AC 代码

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=5e5;
int n;
vector<int>g[N+1];
vector<vector<int>>ans;
int dfn[N+1];
void Tarjan(int x,int fx){
	static int cnt,low[N+1];
	static vector<int>s;
	int son=0;
	dfn[x]=low[x]=++cnt;
	s.push_back(x);
	for(int i:g[x]){
		if(i==fx){
			continue;
		}
		if(!dfn[i]){
			son++;
			Tarjan(i,x);
			low[x]=min(low[x],low[i]);
			if(low[i]>=dfn[x]){
				vector<int>pl;
				while(s.back()!=i){
					pl.push_back(s.back());
					s.pop_back();
				}
				pl.push_back(s.back());
				s.pop_back();
				pl.push_back(x);
				ans.push_back(pl); 
			}
		}else{
			low[x]=min(low[x],dfn[i]);
		}
	}
	if(!fx&&!son){
		ans.push_back({x});
	}
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	
	int m;
	cin>>n>>m;
	while(m--){
		int u,v;
		cin>>u>>v;
		if(u==v){
			continue;
		}
		g[u].push_back(v);
		g[v].push_back(u);
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]){
			Tarjan(i,0);
		}
	}
	cout<<ans.size()<<'\n';
	for(auto &i:ans){
		cout<<i.size()<<' ';
		for(int j:i){
			cout<<j<<' ';
		}
		cout<<'\n';
	}
	
	cout.flush();
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}