无向图 Tarjan 求割点详解

例题链接

割点

所谓割点，就是连通图中的某一个点满足删除该点后，原图不再连通。

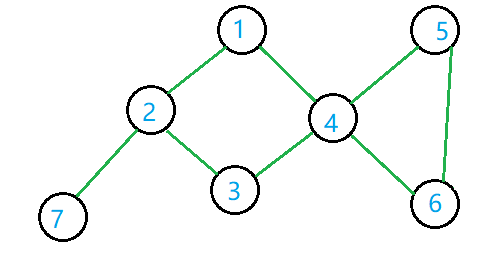
如图中的 \(2,4\) 就是一个割点。

但需要注意的是，割点不一定在环上，比如：

图中的 \(2\) 就是割点。

不过存在特殊情况：

该图没有割点，无论去掉 \(1\) 还是 \(2\)，最后都会剩下一个节点。

关于“割点”不同的定义

如同平衡树中的“左旋”与“右旋”，割点的定义也有不同的说法。（上文是主流说法）

比如说第三张图中只有两个节点，有人认为这两个都是割点，即剩下的那个节点不连通。

无向图 Tarjan 求割点

前置知识：Tarjan 求强连通分量

如果你不会，你可以看看。

无向图 Tarjan 求割点

前向边与横边不存在

见此处。

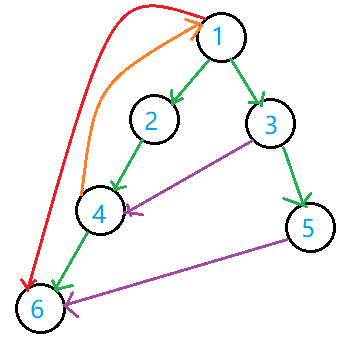
一棵有向图的 DFS 生成树如图：

图中绿色为普通树边，橙色为回溯边，红色为前向边，紫色为横边。

考虑到无向图，实际上 DFS 生成树中只有普通树边和回溯边。

• 前向边不存在，因为无向，因此前向边反向就是一条回溯边。

• 横边不存在，因为按照 DFS 搜索顺序不会使其有可能存在。

  例如图中搜索到 \(4\) 之后，按照 DFS 的原则会先后搜索 \(3,6\)，不可能只搜索 \(6\) 然后回退至 \(1\) 再搜索到 \(3\)，然后连横边。

即化为：

一定不为割点的情况

当该节点是 DFS 生成树的叶节点或只有一个子节点的根节点。

• 叶节点显然不影响生成树的连通。
• 根节点如果只有一个子节点，那么该子节点可以成为新的根节点，不影响连通。

割点的判定

令节点 \(x\) 的子节点为节点 \(y_1,y_2,y_3,\cdots,y_k\)，则删除节点 \(x\) 后其所在连通块会分裂为 \(k+1\) 个部分：\(y_1,y_2,y_3,\cdots,y_k\) 和父节点及其子树。

那么我们需要判断的就是能否使其分裂为至少 \(2\) 个部分。

---

当节点 \(x\) 为根节点时，需要分裂出至少两个符合以下规定的部分。

因为父节点的部分肯定是能够分裂出来的，因此当 \(x\) 不为根节点时，需要分裂出至少一个符合以下规定的部分。

由于 DFS 生成树的性质，\(dfn_{y_i}\) 肯定是大于 \(dfn_x\) 的。

那么 \(low_{y_i}\) 初始时为 \(dfn_{y_i}\) 也大于 \(dfn_x\)。

因此若求出来的 \(low_{y_i}\geq dfn_x\)，则代表其是节点 \(x\) 的子节点部分。

---

但是存在一个问题：如果只需要分裂出一个很好判断，然而当 \(x\) 为根节点时需要判断两个，如何判断 \(y_i\) 之间有没有连接呢？

不需要判断，\(y_i\) 之间绝对没有连接。

由无向图，不存在横边，因此 \(y_i\) 之间想要连接只能够通过公共祖先，然而 \(x\) 为根节点是其子节点的唯一公共祖先。

因此当 \(x\) 为根节点时，\(y_i\) 之间不会相连。

子节点数 son 计算代码：

if(low[v]>=dfn[x])son++;

答案记录：

if(x==root){
    if(son>1)ans.push_back(x);
}else{
    if(son>0)ans.push_back(x);
}

例题 AC 代码

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=5e5,M=2e6;
struct graph{
	struct edge{
		int v,r;
	}a[2*M+1];
	int h[N+1];
	void create(int u,int v){
		static int top=1;
		a[++top]={v,h[u]};
		h[u]=top;
	}
}g;
int dfn[N+1];
vector<int>ans;
void Tarjan(int x,int root){
	static int cnt,low[N+1];
	dfn[x]=low[x]=++cnt;
	int son=0;
	for(int i=g.h[x];i;i=g.a[i].r){
		int &v=g.a[i].v;
		if(!dfn[v]){
			Tarjan(v,root);
			low[x]=min(low[x],low[v]);
			if(low[v]>=dfn[x])son++;
		}else low[x]=min(low[x],dfn[v]);
	}
	if(x==root){
		if(son>1)ans.push_back(x);
	}else{
		if(son>0)ans.push_back(x);
	}
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	int n,m;
	scanf("%d %d",&n,&m);
	for(int i=1;i<=m;i++){
		int u,v;
		scanf("%d %d",&u,&v);
		g.create(u,v);
		g.create(v,u);
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i])Tarjan(i,i);
	}
	sort(ans.begin(),ans.end());
	printf("%d\n",ans.size());
	for(int &i:ans)printf("%d ",i);
	putchar(10);
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}