浅谈平衡树

平衡树是什么

二叉搜索树 BST

BST，二叉搜索树，又名二叉查找树、二叉排序树，是一种特殊的二叉树。能够保证中序遍历是有序的。

最理想的情况下，BST 的树高为 \(\mathcal O(\log n)\)，但是可能会变成 \(\mathcal O(n)\)。

维持树高

一棵较为理想的 BST：

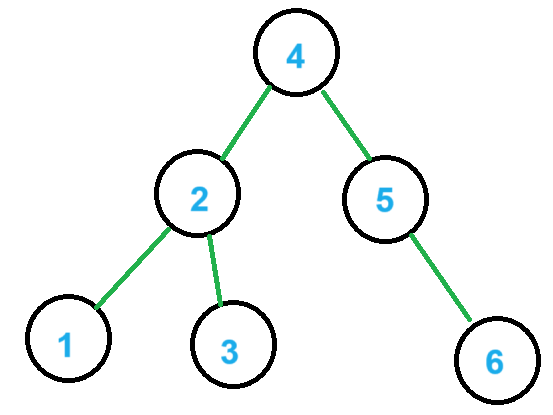
但是可能会因为输入顺序等原因变为：

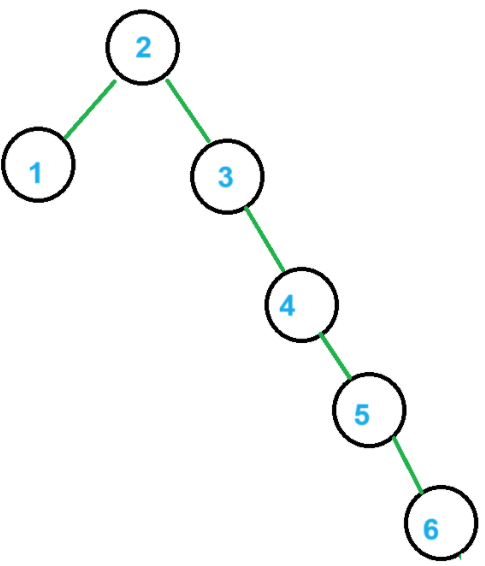
这样就很不好。

因此，我们可以通过各种平衡树来使树高维持在 \(\mathcal O(\log n)\) 。

实现方式

平衡树的实现方式有很多，平衡树更多的是一个概念上的数据结构，没有固定样式。

一般来讲，能够实现普通平衡树中的四个基础操作（插入、删除、查排名、查第 \(k\) 大）的数据结构都能够称之为平衡树。

比如说 01Trie，比如说 FHQ Treap。

甚至于，权值树状数组、权值线段树也能够算作平衡树。

平衡树的原理

平衡树主要原理就是限制树高或者大小。

重构

替罪羊树。

替罪羊树的原理就是当左右两个子树的大小差别超过一定量的时候，就将子树（不是整棵树）放入数组重构。

随机选择父节点

Treap 与 FHQ Treap。

平衡树需要抉择的无非就是树高。

那么对于两个节点，随机选择一个当作父节点，可以证明每一个节点的期望高度都是 \(\mathcal O(\log n)\)。

旋转

AVL 树。

AVL 树会设置一个平衡因子并维护子树高度。当左、右两棵子树的高度差大于等于平衡因子的时候就进行旋转，来保证高度差小于等于 \(1\)。

旋转

旋转是一个很重要的操作。分四种类型：

• LL 型：$T$ 的左孩子的左子树过长
右旋节点 $T$。
• RR 型：$T$ 的右孩子的右子树过长
左旋节点 $T$。
• LR 型：$T$ 的左孩子的右子树过长
左旋节点 $L$ 成为LL型再右旋节点 $T$。
• RL 型：$T$ 的右孩子的左子树过长
右旋节点 $R$ 成为RR型再左旋节点 $T$。

---

事实上，左旋和右旋很多时候是混的……因为不同人对于这俩的叫法不一样……

值得一提的是，大多数情况下，右旋是将左孩子转上去，左旋是将右孩子转下来。

然而 AVL 树存在四种情况，导致代码过长，一般不会用于 OI。

旋转至根节点

Splay 树。

Splay 树通过不断将操作的节点旋转至根节点来使得均摊复杂度为 \(\mathcal O(\log n)\)。

01Trie

按照二进制位来存储，插入、删除类似于字符串，求排名可以给叶子节点赋权值求和，查第 \(k\) 大同理。

权值树状数组

需要离散化。

权值线段树

需要离散化。