浅谈 01Trie
前置知识:Trie树
例题:最大异或对
给定 \(a_1,a_2,a_3,\cdots,a_n\),求 \(a_i\oplus a_j\) 的最大值,其中“\(\oplus\)”表示异或。
我们先分析一下:当什么时候,\(a_i \oplus a_j\) 会尽可能大?
显然,\(a_i,a_j\) 在二进制下高位不同时会尽可能大,因为 \(2^k>2^{k-1}+2^{k-2}+2^{k-3}+\cdots+2^0\)。
因此对于 \(a_i\),能够使 \(a_i \oplus a_j\) 尽可能大的 \(a_j\),一定是高位尽可能不同的。
01Trie 数据结构
众所周知,Trie树是用来存储字符串的,然而我们若是将一个数的二进制视为字符串,同样能够存入Trie中。
即一个字符集为 \(\set{0,1}\) 的 Trie树。
这样的好处就是按照二进制存储。
回顾上文,高位不同,我们在 01Trie 上从高到低尽可能查找高位不同的数即可(如果没有就选择相同的)。最终路径即使 \(a_i \oplus a_j\) 最大的 \(a_j\) 的二进制。
此时我们再将 \(a_i\oplus a_j\) 算出来即可。
这样查找一次的时间复杂度是 \(\mathcal O\left(\log n\right)\) 的,但其实每次都是 \(\mathcal O(32)\),因为 int 有 \(32\) 位。
那么对于每一个 \(a_i\),都这么做一次,最后取最大值,我们就能够在 \(\mathcal O\left(n\log n\right)\) 的时间内解决此问题。
AC 代码
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
const int N=100000;
struct trie{
struct node{
int m[2];
}t[32*N+1];
void insert(int x){
static int top=1;
int p=1;
for(int i=31;i>=0;i--){
int bit=x>>i&1;
if(!t[p].m[bit])t[p].m[bit]=++top;
p=t[p].m[bit];
}
}
int query(int x){
int p=1,ans=0;
for(int i=31;i>=0;i--){
int bit=x>>i&1;
if(t[p].m[!bit]){
p=t[p].m[!bit];
ans|=(!bit)<<i;//注意不要混用逻辑运算符!和位运算符~,~0=111...111,而不是1.
}else{
p=t[p].m[bit];
ans|=bit<<i;
}
}return ans;
}
}trie01;
int n,a[N+1];
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",a+i);
trie01.insert(a[i]);
}
int Max=0;
for(int i=1;i<=n;i++){
Max=max(Max,a[i]^trie01.query(a[i]));
}
printf("%d\n",Max);
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
例题:最长异或路径
题目要求在点 \(u\) 和点 \(v\) 的路径上的权值异或和。
这条路径肯定形如:
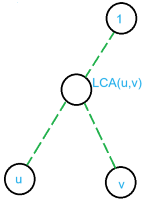
也就是说,\(u\sim v\) 的权值异或和为 \(u\sim LCA(u,v)\) 的异或和异或上 \(LCA(u,v)\sim v\) 的异或和。
令 \(f(u,v)\) 表示 \(u\sim v\) 的路径上的权值异或和。
考虑到一个原理:\(a\oplus a\oplus b=0\oplus b=b\)。
则有:
显然,\(f(1,u)\) 和 \(f(1,v)\) 都可以预处理出来。
那么这就和上一道例题一模一样了。
AC 代码
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=100000;
struct edge{
int v,r,w;
}a[2*(N-1)+1];
int n,h[N+1],value[N+1];
void create(int u,int v,int w){
static int top;
a[++top]={v,h[u],w};
h[u]=top;
}
void dfs(int x,int fx){
for(int i=h[x];i;i=a[i].r){
if(a[i].v!=fx){
value[a[i].v]=value[x]^a[i].w;
dfs(a[i].v,x);
}
}
}
struct trie{
struct node{
int m[2];
}t[32*N+1];
void insert(int x){
static int top=1;
int p=1;
for(int i=31;i>=0;i--){
int bit=x>>i&1;
if(!t[p].m[bit])t[p].m[bit]=++top;
p=t[p].m[bit];
}
}
void build(){
for(int i=1;i<=n;i++){
insert(value[i]);
}
}
int query(int x){
int p=1,ans=0;
for(int i=31;i>=0;i--){
int bit=x>>i&1;
if(t[p].m[!bit]){
p=t[p].m[!bit];
ans|=(!bit)<<i;
}else{
p=t[p].m[bit];
ans|=bit<<i;
}
}return ans;
}
}trie01;
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
scanf("%d",&n);
for(int i=1;i<n;i++){
int u,v,w;
scanf("%d %d %d",&u,&v,&w);
create(u,v,w);
create(v,u,w);
}
dfs(1,0);
trie01.build();
int Max=0;
for(int i=1;i<=n;i++){
Max=max(Max,value[i]^trie01.query(value[i]));
}
printf("%d\n",Max);
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
平衡树
引入:求前缀中 \(\leq x\) 的数的个数。
一眼权值树状数组(或平衡树?)。
然而,这需要离散化,需要离线。
如果不能离散化后离线操作呢?
我们可以使用 01Trie 来完成。
具体而言,就是每一次都在 01Trie 上走 \(x\) 的二进制,如果是 \(1\),就加上(走 \(1\) 之前)当前节点的左子树的权值和即可。
而对于取前驱、后继,插入、删除,访问排名、求排名,都可以使用 01Trie 解决。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号