Splay 树详解

前置知识：平衡树。

例题链接。例题加强版链接。

您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：

插入一个数 \(x\)。

删除一个数 \(x\)（若有多个相同的数，应只删除一个）。

定义排名为比当前数小的数的个数 \(+1\)。查询 \(x\) 的排名。

查询数据结构中排名为 \(x\) 的数。

求 \(x\) 的前驱（前驱定义为小于 \(x\)，且最大的数）。

求 \(x\) 的后继（后继定义为大于 \(x\)，且最小的数）。

对于操作 \(3,5,6\)，不保证当前数据结构中存在数 \(x\)。

Splay 树核心思路是通过 splay 操作不断将操作节点旋转到根节点，从而保证均摊复杂度 \(\mathcal O(\log n)\)。

并且，Splay 树其实是 splay 越多越快的，splay 操作次数越多，树的形态也就越平衡。（也就是说，可以尝试随机 splay 几个点，时间消耗可能会有所提升。）

Splay 的各类平衡树操作都是简单的 BST 操作，操作完之后将操作节点 splay 到根节点即可。

Splay 基本结构/操作

以例题为例。

节点维护信息

struct node{
    int value,cnt;
    int size,father,child[2];
}t[N+1];

\(\textit{value}_x\) 为节点实际维护信息，\(\textit{cnt}_x\) 为相同节点个数。\(\textit{size}_x,\textit{father}_x,\textit{child}_{x,0},\textit{child}_{x,1}\) 分别为 \(x\) 子树大小、父节点、左子节点、右子节点。

钦定左子树的值均小于右子树的值。

同时，对于整棵平衡树而言，还需要存储整棵树的根节点 root。

辅助操作

void up(int p){
    t[p].size=t[t[p].child[0]].size+t[p].cnt+t[t[p].child[1]].size;
}
bool check(int p){
    return t[t[p].father].child[1]==p;
}

up 操作用于更新子树大小，check 操作用于判断是左子节点还是右子节点，\(0\) 表示左子节点，\(1\) 表示右子节点。

`rotate` 操作

如图：

先考虑右旋如何操作。

图中需要将 \(1\) 挂到 \(2\) 的右子树上，再将 \(5\) 挂到 \(1\) 的左子树上。

推广到一般情况，需要对节点 \(x\) 进行 rotate 操作，记 \(y=\textit{father}_x,z=\textit{father}_y\)。

则需要断边 \((z,y),(y,x),(x,\textit{child}_{x,1})\)，连边 \((z,x),(x,y),(y,\textit{child}_{x,1})\)。且此时 \(y\) 为新的 \(\textit{child}_{x,1}\)，原来的 \(\textit{child}_{x,1}\) 为新的 \(\textit{child}_{y,0}\)。

注意需要同时更新 \(\textit{child}_0,\textit{child}_1\) 和 \(\textit{father}\)，并且不要影响 \(0\) 号节点，需要特判。

显然，右旋是将左子节点旋转上去，左旋是将右子节点旋转上去。且左旋是与右旋相对的，因此可以通过判断 \(x\) 是 \(\textit{father}_x\) 的左子节点还是右子节点，从而判断是左旋还是右旋。

一定要注意节点信息更改的顺序。记 \(y=\textit{father}_x,z=\textit{father}_y\)，则修改 \(\textit{child}_z\) 之前不应当修改 \(y\) 的父节点，否则 check 函数无法正确判断。同时，不要修改 \(0\) 节点的信息。

void rotate(int x){
    int y=t[x].father,z=t[y].father;
    bool mode=check(x);
    t[y].child[mode]=t[x].child[!mode];
    t[x].child[!mode]=y;
    if(z){
        t[z].child[check(y)]=x;
    }
    if(t[y].child[mode]){
        t[t[y].child[mode]].father=y;
    }
    t[y].father=x; 
    t[x].father=z;
    up(y);
    up(x);
}

`splay` 操作

splay 操作是 Splay 树的核心操作。如同 FHQ Treap 的 split 操作与 merge 操作。

splay 操作用于将节点 \(x\) 通过 rotate 操作旋转至根节点。

假设对 \(x\) 进行 splay 操作，记 \(p\) 为本次 rotate 操作之前的 \(\textit{father}_x\)，\(g\) 为本次 rotate 操作之前的 \(\textit{father}_p\)。

zig 与 zag

zig 指代此处的右旋（将左孩子转上去），zag 指代左旋（将右孩子转下来）。

splay 操作中途有三种具体操作：

zig 与 zag 操作：当 \(p\) 为根节点时，直接 rotate 一次即可。
zig-zig 与 zag-zag 操作：当 \(p\) 不为根节点，且 \(x,p\) 为同侧子节点时，先 rotate 一次 \(p\)，再 rotate 一次 \(x\) 即可。

如图：
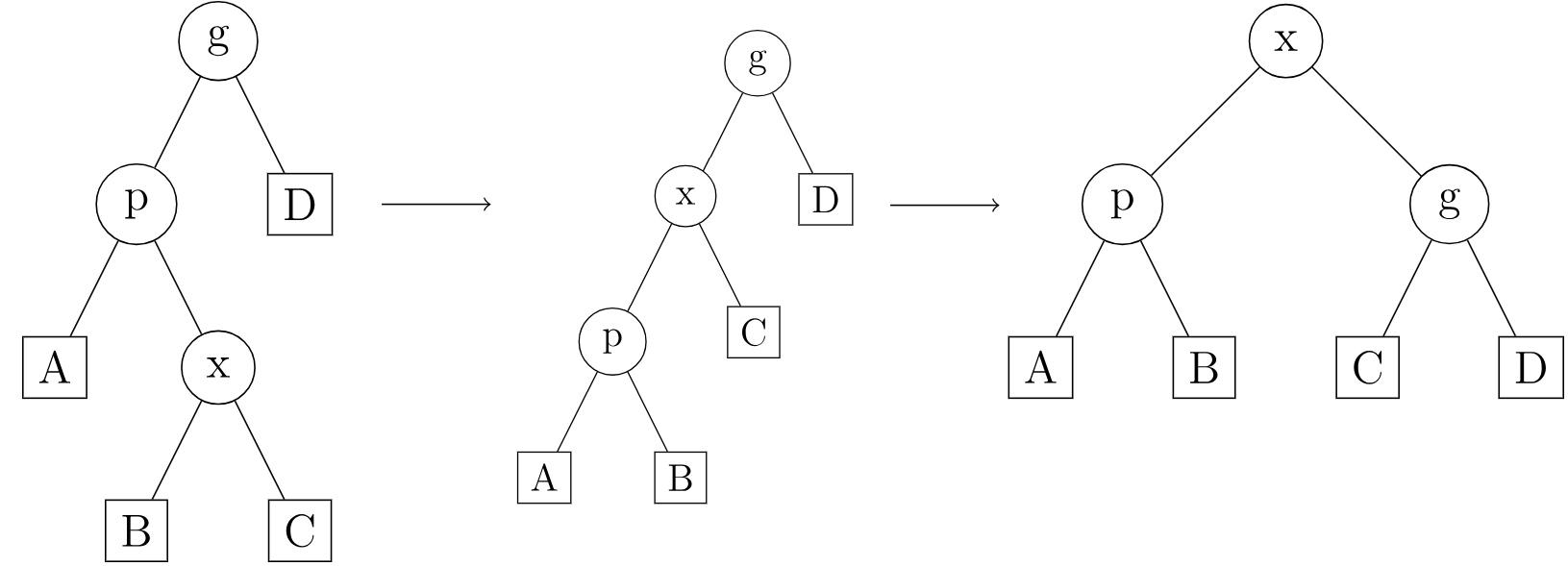
zig-zag 与 zag-zig 操作：当 \(p\) 不为根节点，且 \(x,p\) 为异侧子节点时，先 rotate 一次 \(x\)，此时 \(\textit{father}_x=g\)，再 rotate 一次 \(x\) 即可。

这样可以将 \(x\) rotate 上去的同时，将 \(p\) 也抬升一层，从而保证均摊复杂度。

如图：

int splay(int x){
    while(t[x].father){
        int p=t[x].father;
        if(!t[p].father){
            rotate(x);
            break;
        }
        if(check(p)==check(x)){
            rotate(p);
            rotate(x);
        }else{
            rotate(x);
            rotate(x);
        }
    }
    return x;
}

查找元素

Splay 与 FHQ Treap 暴力分裂不同，Splay 的很多操作都是在 BST 上完成的，因此需要在 BST 上查找元素。查找完成后，将其 splay 到根节点，也有利于各种操作的实现。

特别地，若查询值为 \(x\) 的节点不存在时，应当查找到其前驱/后继节点。

int find(int x){
    int p=root;
    while(true){
        if(t[p].value==x){
            break;
        }else if(x<t[p].value){
            if(!t[p].child[0]){
                break;
            }else{
                p=t[p].child[0];
            }
        }else{
            if(!t[p].child[1]){
                break;
            }else{
                p=t[p].child[1];
            }
        } 
    }
    return root=splay(p);
}

同样不难写出按排名查找的代码：

int kth(int k,int p=root){
    while(true){
        if(t[t[p].child[0]].size+1<=k&&k<=t[t[p].child[0]].size+t[p].cnt){
            break;
        }else if(k<t[t[p].child[0]].size+1){
            p=t[p].child[0];
        }else{
            k-=t[t[p].child[0]].size+t[p].cnt;
            p=t[p].child[1]; 
        }
    }
    root=splay(p);
    return t[root].value;
}

Splay 平衡树操作

插入节点

比较简单，在 BST 上查找，最终要么找到值同样为 \(x\) 的节点，修改 \(\textit{cnt}\) 即可；否则最终会找到一个空节点，创建节点并挂到父节点上，再 splay 到根节点即可。

注意插入完成后要进行一次 up 操作。特判空树。

void insert(int x){
    if(!root){
        root=create(x);
        return;
    }
    int p=root;
    while(true){
        if(t[p].value==x){
            t[p].cnt++;
            break;
        }else if(x<t[p].value){
            if(!t[p].child[0]){
                t[p].child[0]=create(x);
                t[t[p].child[0]].father=p;
                p=t[p].child[0];
                break;
            }else{
                p=t[p].child[0];
            }
        }else{
            if(!t[p].child[1]){
                t[p].child[1]=create(x);
                t[t[p].child[1]].father=p;
                p=t[p].child[1];
                break;
            }else{
                p=t[p].child[1];
            }
        }
    }
    up(p);
    root=splay(p);
}

删除节点

通过 find 找到待删除节点，旋转到根节点。

若根节点的值不是待删除节点，结束操作。
否则将 \(\textit{cnt}_{\textit{root}},\textit{size}_{\textit{root}}\) 减去 \(1\)。
- 若此时 \(\textit{cnt}_{\textit{root}}\neq0\)，结束操作。
- 否则若 \(\textit{cnt}_{\textit{root}}=0\)，则根节点实际上应当被删除。
  
  那么此时的两个子节点 \(p,q\) 就成为了独立的两棵子树，需要将其合并。钦定子树 \(p\) 的值均小于子树 \(q\) 的值。
  
  那么，从子树 \(q\) 中找到一个最小值，将其 splay 到 \(q\) 的父节点，成为新的 \(\textit{root}\) 即可。此时 \(p,q\) 分别为 \(\textit{root}\) 的左右子节点。

void erase(int x){
    find(x);
    if(t[root].value!=x){
        return;
    }
    t[root].cnt--;
    t[root].size--;
    if(t[root].cnt){
        return;
    }
    int p=t[root].child[0],q=t[root].child[1];
    t[p].father=t[q].father=0;
    if(!p||!q){
        root=p|q;
        return;
    }
    kth(1,q);
    t[root].child[0]=p;
    t[p].father=root;
    up(root);
}

查询排名

令待查询节点为 \(x\)。

首先可以通过 find 找出其 \(x\) 或者前驱/后继，并旋转到根节点 \(\textit{root}\)。

若 \(\textit{value}_{\textit{root}}<x\)，则说明 \(\textit{root}\) 是 \(x\) 的前驱，因此可以直接得到答案 \(\textit{size}_{\textit{child}_{\textit{root},0}}+\textit{cnt}_{\textit{root}}+1\)。
否则 \(x\leq\textit{value}_{\textit{root}}\)，则说明左子树 \(\textit{child}_{\textit{root},0}\) 内即所有小于 \(x\) 的数。因此可以得到答案 \(\textit{size}_{\textit{child}_{\textit{root},0}}+1\)。

int rank(int x){
    find(x);
    if(t[root].value<x){
        return t[t[root].child[0]].size+t[root].cnt+1;
    }else{
        return t[t[root].child[0]].size+1;
    }
}

查询前驱

首先显然可以 find 一次。若 \(\textit{value}_{\textit{root}}<x\)，则说明 \(\textit{root}\) 是 \(x\) 的前驱，答案即 \(\textit{value}_{\textit{root}}\)。

否则答案即左子树中的最大值。

int prev(int x){
    find(x);
    if(t[root].value<x){
        return t[root].value;
    }
    int p=t[root].child[0];
    while(t[p].child[1]){
        p=t[p].child[1];
    }
    root=splay(p);
    return t[root].value;
}

查询后继

与查询前驱同理。

int next(int x){
    find(x);
    if(x<t[root].value){
        return t[root].value;
    }
    int p=t[root].child[1];
    while(t[p].child[0]){
        p=t[p].child[0];
    }
    root=splay(p);
    return t[root].value;
}

分裂与合并

Splay 同样可以完成 FHQ Treap 的分裂/合并操作。

先考虑合并，但其实删除节点时，根节点被删除之后就是一次合并两棵 Splay 树的操作。

对于 \(p,q\)，保证 \(p\) 中节点值小于 \(q\) 中节点值，把 \(q\) 的最小值 splay 到根，然后把 \(p\) 挂载 \(q\) 的左子节点即可。

对于分裂，将 \(x\) splay 到根，然后断开左子树的边即可。

例题 AC 代码

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=1e5;
struct Splay{
	static int root;
	int size;
	struct node{
		int value,cnt;
		int size,father,child[2];
	}t[N+1];
	
	void up(int p){
		t[p].size=t[t[p].child[0]].size+t[p].cnt+t[t[p].child[1]].size;
	}
	bool check(int p){
		return t[t[p].father].child[1]==p;
	}
	void rotate(int x){
		int y=t[x].father,z=t[y].father;
		bool mode=check(x);
		t[y].child[mode]=t[x].child[!mode];
		t[x].child[!mode]=y;
		if(z){
			t[z].child[check(y)]=x;
		}
		if(t[y].child[mode]){
			t[t[y].child[mode]].father=y;
		}
		t[y].father=x; 
		t[x].father=z;
		up(y);
		up(x);
	}
	int splay(int x){
		while(t[x].father){
			int p=t[x].father;
			if(!t[p].father){
				rotate(x);
				break;
			}
			if(check(p)==check(x)){
				rotate(p);
				rotate(x);
			}else{
				rotate(x);
				rotate(x);
			}
		}
		return x;
	}
	int create(int x){
		t[++size]={x,1,1};
		return size;
	}
	void insert(int x){
		if(!root){
			root=create(x);
			return;
		}
		int p=root;
		while(true){
			if(t[p].value==x){
				t[p].cnt++;
				break;
			}else if(x<t[p].value){
				if(!t[p].child[0]){
					t[p].child[0]=create(x);
					t[t[p].child[0]].father=p;
					p=t[p].child[0];
					break;
				}else{
					p=t[p].child[0];
				}
			}else{
				if(!t[p].child[1]){
					t[p].child[1]=create(x);
					t[t[p].child[1]].father=p;
					p=t[p].child[1];
					break;
				}else{
					p=t[p].child[1];
				}
			}
		}
		up(p);
		root=splay(p);
	}
	int find(int x){
		int p=root;
		while(true){
			if(t[p].value==x){
				break;
			}else if(x<t[p].value){
				if(!t[p].child[0]){
					break;
				}else{
					p=t[p].child[0];
				}
			}else{
				if(!t[p].child[1]){
					break;
				}else{
					p=t[p].child[1];
				}
			} 
		}
		return root=splay(p);
	}
	void erase(int x){
		find(x);
		if(t[root].value!=x){
			return;
		}
		t[root].cnt--;
		t[root].size--;
		if(t[root].cnt){
			return;
		}
		int p=t[root].child[0],q=t[root].child[1];
		t[p].father=t[q].father=0;
		if(!p||!q){
			root=p|q;
			return;
		}
		kth(1,q);
		t[root].child[0]=p;
		t[p].father=root;
		up(root);
	}
	int rank(int x){
		find(x);
		if(t[root].value<x){
			return t[t[root].child[0]].size+t[root].cnt+1;
		}else{
			return t[t[root].child[0]].size+1;
		}
	}
	int kth(int k,int p=root){
		while(true){
			if(t[t[p].child[0]].size+1<=k&&k<=t[t[p].child[0]].size+t[p].cnt){
				break;
			}else if(k<t[t[p].child[0]].size+1){
				p=t[p].child[0];
			}else{
				k-=t[t[p].child[0]].size+t[p].cnt;
				p=t[p].child[1]; 
			}
		}
		root=splay(p);
		return t[root].value;
	}
	int prev(int x){
		find(x);
		if(t[root].value<x){
			return t[root].value;
		}
		int p=t[root].child[0];
		while(t[p].child[1]){
			p=t[p].child[1];
		}
		root=splay(p);
		return t[root].value;
	}
	int next(int x){
		find(x);
		if(x<t[root].value){
			return t[root].value;
		}
		int p=t[root].child[1];
		while(t[p].child[0]){
			p=t[p].child[0];
		}
		root=splay(p);
		return t[root].value;
	}
	void print(int p=root){
		if(!p){
			return;
		}
		print(t[p].child[0]);
		for(int i=1;i<=t[p].cnt;i++){
			cerr<<t[p].value<<' ';
		}
		print(t[p].child[1]);
	}
}t;
int Splay::root;
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	
	int n;
	cin>>n;
	while(n--){
		int opt,x;
		cin>>opt>>x;
		switch(opt){
			case 1:
				t.insert(x);
				break;
			case 2:
				t.erase(x);
				break;
			case 3:
				cout<<t.rank(x)<<'\n';
				break;
			case 4:
				cout<<t.kth(x)<<'\n';
				break;
			case 5:
				cout<<t.prev(x)<<'\n';
				break;
			case 6:
				cout<<t.next(x)<<'\n';
				break;
		}
	}
	
	cout.flush();
	 
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

Splay 与可持久化

Splay 是不能可持久化的，因为 Splay 的复杂度是基于势能均摊得到的。

只有复杂度严格一致或是期望一致的数据结构才能可持久化。

否则例如 Splay，可以构造一种情况需要将深度为 \(\mathcal O(n)\) 的节点 splay 到根节点，可持久化每一次都是这个版本，复杂度就变为了 \(\mathcal O(mn)\)。

~~所以还是写 FHQ Treap 吧。~~

Splay 区间操作

Splay 因为可以分裂/合并，因此可以模拟 FHQ Treap 维护区间。时间复杂度 \(\mathcal O(m\log n)\)。

但是，存在更好写，也更应用 Splay 特性的区间操作写法。

Luogu P3391 文艺平衡树

维护一个有序序列 \(a_1,a_2,\cdots,a_n\)，初始 \(a_i=i\)。给定 \(m\) 次操作，每次翻转区间 \([l,r]\)。

求 \(m\) 次操作之后的序列。

对于 \(100\%\) 的数据，\(1\leq n,m\leq100000\)。

建树

Splay 维护序列建树其实很简单，直接构造一条链即可。

由于 Splay 操作区间 \([l,r]\) 的时候，需要用到节点 \(l-1,r+1\)，因此还要插入 \(0\) 和 \(n+1\) 号节点，给这两个点赋一个特殊值即可。

void build(int n,int a[]){
    root=create(inf);
    for(int i=1;i<=n;i++){
        int p=create(a[i]);
        t[root].father=p;
        t[p].child[0]=root;
        up(p);
        root=p;
    }
    int p=create(inf);
    t[root].father=p;
    t[p].child[0]=root;
    up(p);
    root=p;
}

区间操作

首先，找到 \(l-1,r+1\) 对应的节点 \(\textit{pl},\textit{pr}\)。

将 \(\textit{pl}\) splay 到根，再把 \(\textit{pr}\) splay 到 \(\textit{pl}\) 的右子节点。

此时，\(\textit{pr}\) 的左子树即对应 \([l,r]\)，原因显然。

维护懒标记操作即可。

void reverse(int l,int r){
    l++,r++;
    int pl=kth(l-1),pr=kth(r+1);
    root=splay(pl);
    t[t[pl].child[1]].father=0;
    t[pl].child[1]=splay(pr);
    t[pr].father=pl;
    t[t[pr].child[0]].tag^=1;
}

懒标记

由于懒标记涉及左右子树信息更新，因此在按排名查找 kth 时，需要先下传更新。之后 splay、rotate 上去时，因为标记已经下放完了，所以不用管。

如果没有下放标记，你把 down 写在 rotate 里面是错的，因为标记要从上往下下放，不然你下放了又有新的。

所以在 LCT 之类的东西里面，还要再写一个 update 来先下放所有标记。

void down(int p){
    if(t[p].tag){
        t[t[p].child[0]].tag^=1;
        t[t[p].child[1]].tag^=1;
        swap(t[p].child[0],t[p].child[1]);
        t[p].tag=0;
    }
}
void rotate(int x){
    int y=t[x].father,z=t[y].father;
    bool mode=check(x);
    t[y].child[mode]=t[x].child[!mode];
    t[x].child[!mode]=y;
    if(z){
        t[z].child[check(y)]=x;
    }
    if(t[y].child[mode]){
        t[t[y].child[mode]].father=y;
    }
    t[y].father=x;
    t[x].father=z;
    up(y);
    up(x);
}
int kth(int k,int p){
    while(true){
        down(p);
        if(t[t[p].child[0]].size+1==k){
            break;
        }else if(k<t[t[p].child[0]].size+1){
            p=t[p].child[0];
        }else{
            k-=t[t[p].child[0]].size+1;
            p=t[p].child[1];
        }
    }
    return p;
}

参考代码

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=100000,inf=0x3f3f3f3f;
int n,a[N+1];
struct Splay{
	int root,size;
	struct node{
		int value;
		int size,father,child[2];
		
		bool tag;
	}t[N+2+1];
	
	void up(int p){
		t[p].size=t[t[p].child[0]].size+1+t[t[p].child[1]].size;
	}
	bool check(int p){
		return t[t[p].father].child[1]==p;
	}
	int create(int x){
		t[++size]={x,1};
		return size;
	}
	void build(int n,int a[]){
		root=create(inf);
		for(int i=1;i<=n;i++){
			int p=create(a[i]);
			t[root].father=p;
			t[p].child[0]=root;
			up(p);
			root=p;
		}
		int p=create(inf);
		t[root].father=p;
		t[p].child[0]=root;
		up(p);
		root=p;
	}
	void down(int p){
		if(t[p].tag){
			t[t[p].child[0]].tag^=1;
			t[t[p].child[1]].tag^=1;
			swap(t[p].child[0],t[p].child[1]);
			t[p].tag=0;
		}
	}
	void rotate(int x){
		int y=t[x].father,z=t[y].father;
		bool mode=check(x);
		t[y].child[mode]=t[x].child[!mode];
		t[x].child[!mode]=y;
		if(z){
			t[z].child[check(y)]=x;
		}
		if(t[y].child[mode]){
			t[t[y].child[mode]].father=y;
		}
		t[y].father=x;
		t[x].father=z;
		up(y);
		up(x);
	}
	int splay(int x){
		while(t[x].father){
			int p=t[x].father;
			if(!t[p].father){
				rotate(x);
				break;
			}
			if(check(p)==check(x)){
				rotate(p);
				rotate(x);
			}else{
				rotate(x);
				rotate(x);
			}
		}
		return x;
	}
	int kth(int k,int p){
		while(true){
			down(p);
			if(t[t[p].child[0]].size+1==k){
				break;
			}else if(k<t[t[p].child[0]].size+1){
				p=t[p].child[0];
			}else{
				k-=t[t[p].child[0]].size+1;
				p=t[p].child[1];
			}
		}
		return p;
	}
	int kth(int k){
		return kth(k,root);
	}
	void reverse(int l,int r){
		l++,r++;
		int pl=kth(l-1),pr=kth(r+1);
		root=splay(pl);
		t[t[pl].child[1]].father=0;
		t[pl].child[1]=splay(pr);
		t[pr].father=pl;
		t[t[pr].child[0]].tag^=1;
	}
	void print(int p){
		if(!p){
			return;
		}
		down(p);
		print(t[p].child[0]);
		if(t[p].value!=inf){
			cout<<t[p].value<<' ';
		}
		print(t[p].child[1]);
	}
	void print(){
		print(root);
	}
}t;
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	
	int m;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		a[i]=i;
	}
	t.build(n,a);
	while(m--){
		int l,r;
		cin>>l>>r;
		t.reverse(l,r);
	}
	t.print();
	
	cout.flush();
	 
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

posted @ 2025-07-20 23:17 TH911 阅读(65) 评论(0) 收藏举报

刷新页面返回顶部

TH911 Blog

光阴不可测，岁月亦无歌。

Splay 树详解

Splay 基本结构/操作

节点维护信息

辅助操作

`rotate` 操作

`splay` 操作

查找元素

Splay 平衡树操作

插入节点

删除节点

查询排名

查询前驱

查询后继

分裂与合并

例题 AC 代码

Splay 与可持久化

Splay 区间操作

建树

区间操作

懒标记

参考代码

公告

TH911 Blog

光阴不可测，岁月亦无歌。

Splay 树详解

Splay 基本结构/操作

节点维护信息

辅助操作

rotate 操作

splay 操作

查找元素

Splay 平衡树操作

插入节点

删除节点

查询排名

查询前驱

查询后继

分裂与合并

例题 AC 代码

Splay 与可持久化

Splay 区间操作

建树

区间操作

懒标记

参考代码

公告

`rotate` 操作

`splay` 操作