直接法中雅可比的理解

咱们要的是「相机调一点点位置，像素颜色误差会变多少」（这是指导相机调整的核心依据），但这个关系没法直接算，所以拆成两步：
相机位置调整 → 像素坐标(u,v)变化 → 像素颜色(灰度)变化 → 颜色误差变化
J_pixel_xi：管第一步（相机调整 → 像素坐标变多少）；
J_img_pixel：管第二步（像素坐标变 → 颜色变多少）；
合起来就能算出「相机调整 → 颜色误差变多少」，相机就知道 “往哪个方向调，误差会变小”。
第一部分：J_pixel_xi（相机调整 ↔ 像素坐标的关系）

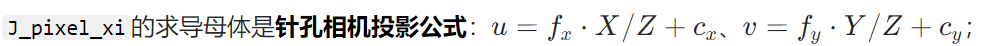
先回忆李代数 ξ 的 6 个维度（相机的 6 个调整方向）：
ξ = [ρx, ρy, ρz, φx, φy, φz]
前 3 个（ρx/ρy/ρz）：相机的平移（沿 x/y/z 轴挪，单位：米）；
后 3 个（φx/φy/φz）：相机的旋转（绕 x/y/z 轴转，单位：弧度）；
J_pixel_xi 是个 2 行 6 列的矩阵，每一行对应一个像素坐标（u 行、v 行），每一列对应一个调整方向（ρx 列、ρy 列…φz 列），每个值的意思是：“相机沿这个方向调 1 单位，像素坐标会变多少个像素”。
逐行讲 J_pixel_xi 的通俗意义（结合直觉，不用记公式）
先明确几个变量的直觉含义：
fx/fy：相机焦距（固定参数，越大，画面里的东西显得越大）；
X/Y/Z：当前点在相机坐标系下的 3D 坐标（Z 是深度，离相机的距离）；
Z_inv=1/Z，Z2_inv=1/Z²：深度的倒数，离得越近（Z 越小），这个值越大。
1. 平移部分（前 3 列：ρx/ρy/ρz）—— 相机挪一挪，像素怎么动

点击查看代码

// u对平移的偏导（u行，前3列）
J_pixel_xi(0, 0) = fx * Z_inv;  // ∂u/∂ρx：相机沿x轴挪1米，u变 fx/Z 个像素
J_pixel_xi(0, 1) = 0;            // ∂u/∂ρy：相机沿y轴挪，u几乎不变（直觉：左右挪不影响水平像素？错！是推导后y平移对u的影响为0）
J_pixel_xi(0, 2) = -fx * X * Z2_inv;  // ∂u/∂ρz：相机沿z轴（前后）挪1米，u变 -fx*X/Z² 个像素

// v对平移的偏导（v行，前3列）
J_pixel_xi(1, 0) = 0;            // ∂v/∂ρx：相机沿x轴挪，v几乎不变
J_pixel_xi(1, 1) = fy * Z_inv;  // ∂v/∂ρy：相机沿y轴挪1米，v变 fy/Z 个像素
J_pixel_xi(1, 2) = -fy * Y * Z2_inv;  // ∂v/∂ρz：相机沿z轴挪1米，v变 -fy*Y/Z² 个像素

举个直觉例子：
比如一个点离相机 Z=2 米，fx=700，那么∂u/∂ρx=700/2=350—— 意思是「相机沿 x 轴往右挪 1 米，这个点在画面里的 u 坐标（水平位置）会往右移 350 个像素」。
符合直觉：离得越近（Z 越小），相机挪一点点，画面里的点动得越多（比如离你 1 米的杯子，你挪 1 步，杯子在画面里动很多；离你 100 米的树，你挪 1 步，树几乎不动）。
2. 旋转部分（后 3 列：φx/φy/φz）—— 相机转一转，像素怎么动？

点击查看代码

// u对旋转的偏导（u行，后3列）
J_pixel_xi(0, 3) = -fx * X * Y * Z2_inv;    // ∂u/∂φx：绕x轴转1弧度，u变多少
J_pixel_xi(0, 4) = fx + fx * X * X * Z2_inv;// ∂u/∂φy：绕y轴转1弧度，u变多少
J_pixel_xi(0, 5) = -fx * Y * Z_inv;         // ∂u/∂φz：绕z轴转1弧度，u变多少

// v对旋转的偏导（v行，后3列）
J_pixel_xi(1, 3) = -fy - fy * Y * Y * Z2_inv; // ∂v/∂φx：绕x轴转1弧度，v变多少
J_pixel_xi(1, 4) = fy * X * Y * Z2_inv;       // ∂v/∂φy：绕y轴转1弧度，v变多少
J_pixel_xi(1, 5) = fy * X * Z_inv;            // ∂v/∂φz：绕z轴转1弧度，v变多少

旋转的影响比平移复杂（因为旋转会同时改变 X/Y/Z 的相对位置），但本质还是「相机转一点点，像素坐标会动多少」—— 比如绕 z 轴转（左右摇头），∂u/∂φz=-fx*Y/Z_inv，意思是「摇头 1 弧度，水平像素 u 会往左 / 右动，离得越近、Y 越大（上下位置越偏），动得越多」（符合直觉：画面边缘的点，摇头时动得更明显） 总结：J_pixel_xi 的每一个值，都是 “相机调这个方向，像素坐标动多少” 比如 J_pixel_xi (0,0)=350，就是「相机沿 x 轴挪 1 米，u 变 350 像素」；值为 0 就是 “这个方向调整，对该像素坐标没影响”。

第二部分：J_img_pixel（像素坐标 ↔ 颜色灰度的关系）

这个特别简单，就是算像素的梯度—— 梯度的意思是「像素坐标动 1 个像素，颜色灰度会变多少」。
先讲梯度的直觉：
比如画面里有一条黑白分界线，分界线处的梯度很大（u 动 1 像素，灰度从 0 变 255）；纯色区域的梯度很小（u 动 1 像素，灰度几乎不变）。
梯度越大，说明这个点的 “颜色变化敏感”，调整相机时，这个点的参考价值越高（能更精准指导相机调整）。
代码里的计算方式（中心差分）：

点击查看代码

J_img_pixel = Eigen::Vector2d(
    // ∂I/∂u：u方向梯度 = (u+1的灰度 - u-1的灰度)/2
    0.5 * (GetPixelValue(img2, u + 1 + x, v + y) - GetPixelValue(img2, u - 1 + x, v + y)),
    // ∂I/∂v：v方向梯度 = (v+1的灰度 - v-1的灰度)/2
    0.5 * (GetPixelValue(img2, u + x, v + 1 + y) - GetPixelValue(img2, u + x, v - 1 + y))
);

不用 “u+1 - u” 是因为 “中心差分” 比 “前向差分” 更准（比如 u=100.5，u+1=101.5，u-1=99.5，两者的差能更精准反映中间位置的梯度）； 除以 2 是因为两个点之间隔了 2 个像素（u-1 到 u+1 是 2 个像素距离），所以梯度是 “总变化量 / 距离”。 举个例子： 如果 u+1 的灰度是 200，u-1 的灰度是 100，那么∂I/∂u=(200-100)/2=50—— 意思是「u 坐标往右动 1 个像素，灰度会增加 50」。 如果是纯色区域，u+1 和 u-1 的灰度都是 150，那么梯度 = 0—— 这个点对相机调整没帮助（怎么调，颜色都不变）。

最后：两者结合（总雅克比 J）—— 相机调整 ↔ 颜色误差的关系

代码里总雅克比是这么算的：
Vector6d J = -1.0 * (J_img_pixel.transpose() * J_pixel_xi).transpose();
不用管转置这些操作，只记最终效果：
总雅克比 J 是 6 维向量，每一个值代表「相机沿这个方向调 1 单位，颜色误差会变多少」。
如果 J 的第 0 位（对应 ρx）是 - 10，意思是「相机沿 x 轴挪 1 米，颜色误差会减少 10」—— 那相机就该沿 x 轴挪；
如果 J 的第 3 位（对应 φx）是 5，意思是「相机绕 x 轴转 1 弧度，误差会增加 5」—— 那相机就该反方向转。
有了这个总雅克比 J，就能汇总所有点的 J，算出海塞矩阵 H 和误差向量 b，最终解出相机该调整的量 update—— 这就是相机 “精准调整位置” 的全部依据。
J_pixel_xi：告诉你 “相机调哪个方向，像素会动多少”；
J_img_pixel：告诉你 “像素动多少，颜色会变多少”；
合起来：告诉你 “相机调哪个方向，颜色误差会变多少”—— 有了这个，相机就不是瞎猜，而是精准调整。