光流法中逆公式的理解

关键代码解读

点击查看代码

if (inverse == false) {
    // 普通LK：每次迭代重置H和b（H随迭代变）
    H = Eigen::Matrix2d::Zero();
    b = Eigen::Vector2d::Zero();
} else {
    // 逆公式LK：仅重置b，H只算一次（iter==0时）
    b = Eigen::Vector2d::Zero();
}

// 雅克比矩阵计算
if (inverse == false) {
    // 普通LK：J依赖I2的梯度（目标帧，随dx/dy变）
    J = -1.0 * Eigen::Vector2d(
        0.5 * (GetPixelValue(img2, kp.pt.x + dx + x + 1, kp.pt.y + dy + y) -
               GetPixelValue(img2, kp.pt.x + dx + x - 1, kp.pt.y + dy + y)),
        0.5 * (GetPixelValue(img2, kp.pt.x + dx + x, kp.pt.y + dy + y + 1) -
               GetPixelValue(img2, kp.pt.x + dx + x, kp.pt.y + dy + y - 1))
    );
} else if (iter == 0) {
    // 逆公式LK：J仅在第0次迭代算（依赖I1的梯度，固定）
    J = -1.0 * Eigen::Vector2d(
        0.5 * (GetPixelValue(img1, kp.pt.x + x + 1, kp.pt.y + y) -
               GetPixelValue(img1, kp.pt.x + x - 1, kp.pt.y + y)),
        0.5 * (GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y + 1) -
               GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y - 1))
    );
}

// H的更新逻辑
if (inverse == false || iter == 0) {
    H += J * J.transpose();  // 逆公式仅iter==0时更新H
}

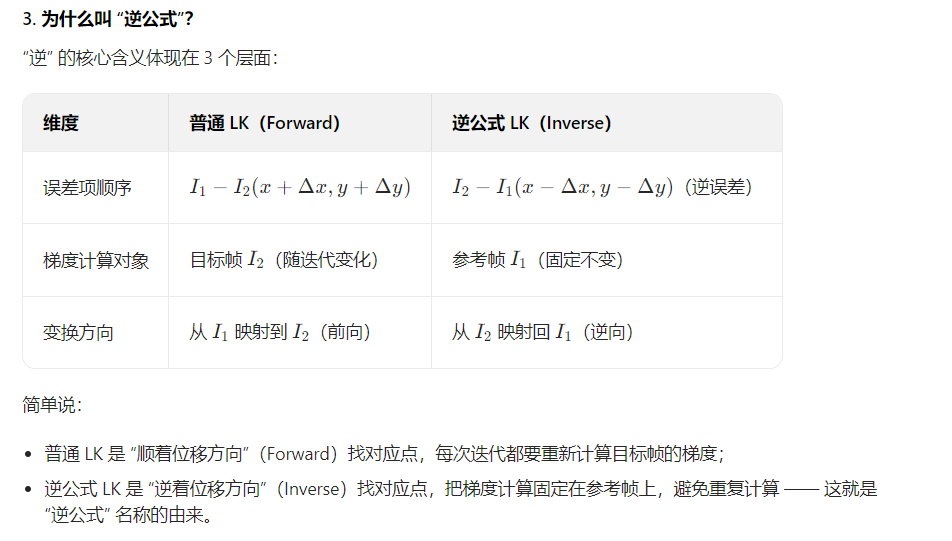
总结

逆公式 LK 的核心优势：将梯度计算固定在参考帧上，海森矩阵只需计算一次，迭代效率远高于普通 LK；
“逆” 的本质：误差项逆序、变换方向逆置、梯度计算对象从目标帧逆转为参考帧；
代码体现：逆公式模式下，H 仅在第一次迭代计算，J 基于参考帧 img1 而非目标帧 img2，大幅减少重复计算。

点击查看代码

// 雅克比矩阵 J 的计算逻辑
if (inverse == false) {
    // 普通LK：每次迭代都基于 I2 重新算 J
    J = ... // 依赖 img2 和当前 dx/dy
} else if (iter == 0) {
    // 逆公式LK：仅在第一次迭代算 J，后续迭代跳过
    J = ... // 仅依赖 img1，和 dx/dy 无关
}

// 海森矩阵 H 的更新逻辑
if (inverse == false || iter == 0) {
    // 普通LK：每次迭代更新 H；逆公式LK：仅第一次迭代更新 H
    H += J * J.transpose();
}