海森矩阵（Hessian Matrix)在高斯牛顿法中的理解

海森矩阵（Hessian Matrix）的核心价值是描述目标函数的局部曲率，它包含了函数的二阶导数信息，这让优化算法能突破 “仅依赖梯度（一阶信息）” 的局限，实现更高效、更精准的寻优。在优化算法中，海森矩阵的应用主要集中在以下几个核心方向：

1. 牛顿法与拟牛顿法：核心的搜索方向指导
   牛顿法是二阶优化算法的代表，它的核心优势是收敛速度快，这完全依赖海森矩阵提供的函数曲率信息，而梯度下降这类一阶算法只用到了梯度（一阶导数）。
   这是海森矩阵最经典、最核心的应用场景，直接决定了优化算法的收敛速度。
   牛顿法（Newton's Method）梯度下降法仅用一阶导数（梯度）确定搜索方向，本质是 “沿着最陡下坡走”，
   

注：海森矩阵正定性的理解


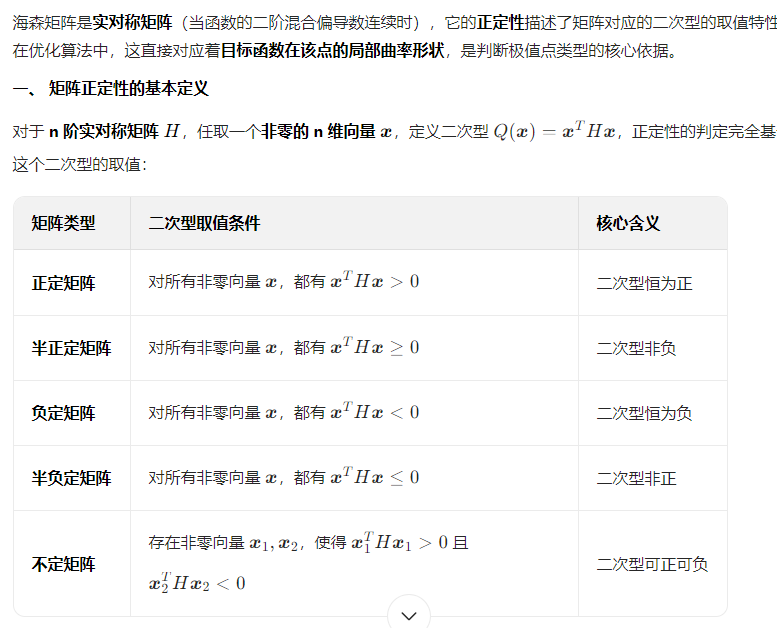
正定性在优化算法中的关键作用