树的直径和重心

\(\text{luogu-1099}\)

给定一颗无根树，\(F\) 是某条直径上的一段路径，其长度不超过 \(s\)。

定义 \(F\) 的偏心距为，无根树上的任意一点到 \(F\) 的距离最大值。

其中，一个点到路径的距离为这个点到路径上任意一点距离的最小值。

求路径 \(F\) 的偏心距的最小值，必要时，\(F\) 可以退化成一个点。

\(2 \le n \le 300\)，\(0 \le s \le 10^3\)，\(1 \le u,v \le n\)，\(0 \le w \le 10^3\)。

---

其实通过手摸数据，可以发现，题中 \(F\) 需要位于直径上的限制可以忽略。

具体证明如下（来自于 题解 P1099 【树网的核】 - 洛谷专栏）：

引理 2.2：若路径存在不位于直径上的部分，这条路径对应的偏心距一定不会比全部位于直径上的路径的偏心距的最小值更小。

证明：原命题等价于，对于任意一条不完全位于（或者完全不位于）直径上的路径 \(F\)，都存在一条完全位于直径上的路径 \(F^\prime\)，使得 \(\operatorname{ECC}(F) \geq \operatorname{ECC}(F^\prime)\)。下面是一个构造性的证明。

简单来说，我们采用如下方法构造：对于一条不完全位于（或者完全不位于）直径上的路径 \(F\)，找到该路径与直径的一个交点 \(m\)（必要时通过延长 \(F\) 来找到交点），然后再证明 \(P(m,m)\) 这条路径至少不会比 \(F\) 更劣。

沿用 引理 2.1 中出现的记号，构建下图（树上的部分节点略去）：

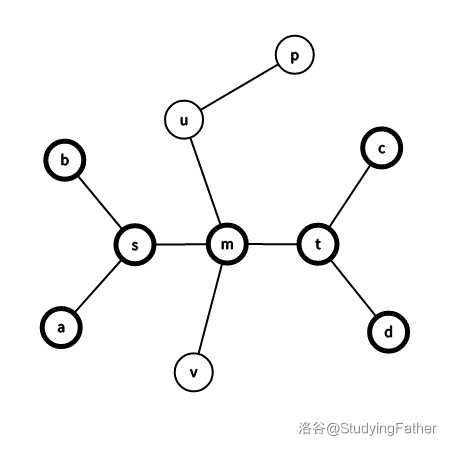
注：

1. 加粗的点一定位于树的某条直径上，未加粗的点一定不位于树的任意一条直径上，即 \(P(p,v)\) 这条路径不是树的直径。
2. 其实原图有多少条直径对本引理证明没有影响，图上保留多条直径只是忘记删了。

现在开始讨论。

1. 考虑 \(P(p,u)\) 这条路径。距离 \(P(p,u)\) 最远的点是哪个点，是 \(v\) 吗？因为，\(P(b,m) + P(m,v) < P(b,m) + P(m,d) = D(b,d)\)，即 \(P(m,v) < P(m,d)\)，因此距离 \(u\) 最远的点，是直径的端点，不是 \(v\) 这样一个不在直径上的点。
2. 现在考虑 \(P(u,v)\) 这条路径。距离 \(P(u,v)\) 最远的点是哪个点，是 \(p\) 吗？如果 \(P(p,u) \geq P(a,m)\)（其余情况同理），则 \(D(a,c) = P(a,m) + P(m,c) \leq P(p,u) + P(m,c) < P(p,u) + P(u,m) + P(m,c) = P(p,c)\)，与 \(D(a,c)\) 是直径矛盾。因此距离 \(P(u,v)\) 最远的点，仍然是直径的端点。
3. 最后考虑 \(P(m,m)\) 这条路径。距离 \(P(m,m)\) 最远的点是哪个点，是 \(p\) 或者 \(v\) 吗？注意到 \(p,v\) 均不在直径上，于是 \(P(b,m) + P(m,p) < P(b,m) + P(m,d) = D(b,d)\)，即 \(P(m,p) < P(m,d)\)（这里只举了 \(p\) 的情况，\(v\) 同理），因此距离 \(P(m,m)\) 最远的点，仍然是直径的端点。

（由于直径是树上最长简单路径这一性质，距离上述三条路径最远的点一定不会在从直径上 \(m\) 之外的其他点引出的支链上取得，因此这些支链没有画出。）

对于 2 和 3 两种情况，偏心距显然为 \(\max\{P(a,m), P(m,c)\}\)，对于 1 这种情况，偏心距为 \(\max\{P(a,m), P(m,c)\} + P(u,m)\)。综上，1 和 2 这两种路径不完全位于（或者完全不位于）直径上的方案，不会比 3 这种完全位于直径上的方案更优。\(\square\)

因此，虽然原题限制路径只能在直径上取得，但可以忽略这一限制考虑所有满足长度限制的路径，而求得的最小偏心距不变。

---

于是我们可以任意取路径，根据题意枚举就可得到答案了。

具体枚举方式如下，先用 Floyd 预处理出两点距离，接着对于路径 \(i \to j\)，枚举节点 \(k\)，那么 \(k\) 到路径 \(i \to j\) 的距离即为 \(\frac{f_{i,k} + f_{j,k} - f_{i,j}}{2}\)，于是 \(i \to j\) 的偏心距则为上式的最大值。

答案就是长度不超过 \(s\) 的路径偏心距的最小值。

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define MAXN 305
#define INF 0x3f3f3f3f

long long read() {
	long long x = 0, f = 1;
	char c = getchar();
	while(c > 57 || c < 48) { if(c == 45) f = -1; c = getchar(); }
	while(c >= 48 && c <= 57) { x = (x << 1) + (x << 3) + (c - 48); c = getchar(); }
	return x * f;
}

long long n, s, f[MAXN][MAXN], ans = INF;

int main() {
	n = read(), s = read(); memset(f, 0x3f, sizeof f);
	for(int i = 1; i <= n; i ++) f[i][i] = 0;
	for(int i = 2; i <= n; i ++) {
		long long x = read(), y = read(), w = read();
		f[x][y] = f[y][x] = min(f[x][y], w);
	}
	for(int k = 1; k <= n; k ++) for(int i = 1; i <= n; i ++)
		for(int j = 1; j <= n; j ++) f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
	for(int i = 1; i <= n; i ++) for(int j = 1; j <= n; j ++)
		if(f[i][j] <= s) {
			long long res = 0;
			for(int k = 1; k <= n; k ++) 
				res = max(res, (f[i][k] + f[j][k] - f[i][j]) / 2);
			ans = min(ans, res);
		}
	cout << ans << "\n";
	return 0;
}

\(\text{luogu-1395}\)

有一个村庄居住着 \(n\) 个村民，有 \(n-1\) 条路径使得这 \(n\) 个村民的家联通，每条路径的长度都为 \(1\)。现在村长希望在某个村民家中召开一场会议，村长希望所有村民到会议地点的距离之和最小，那么村长应该要把会议地点设置在哪个村民的家中，并且这个距离总和最小是多少？若有多个节点都满足条件，则选择节点编号最小的那个点。

\(1 \le n \le 5 \times 10^4\)。

---

实际上就是求树的重心，因为树的重心满足所有点到重心的距离和最小。

#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;
#define MAXN 50005
#define INF 0x3f3f3f3f

long long read() {
	long long x = 0, f = 1;
	char c = getchar();
	while(c > 57 || c < 48) { if(c == 45) f = -1; c = getchar(); }
	while(c >= 48 && c <= 57) { x = (x << 1) + (x << 3) + (c - 48); c = getchar(); }
	return x * f;
}

long long n, si[MAXN], sz[MAXN], w[MAXN], ans = INF, res;
vector<long long> v[MAXN];

void dfs(long long x, long long fa) {
	si[x] = 1, w[x] = 0;
	for(auto y : v[x]) if(y != fa)
		dfs(y, x), si[x] += si[y], w[x] = max(w[x], si[y]);
	w[x] = max(w[x], n - si[x]);
	if(w[x] <= n / 2) ans = min(ans, x);
	return;
}

void dfs1(long long x, long long fa) {
	if(x != ans) sz[x] = sz[fa] + 1;
	for(auto y : v[x]) if(y != fa) dfs1(y, x);
	return;
}

int main() {
	n = read();
	for(int i = 2; i <= n; i ++) {
		long long x = read(), y = read();
		v[x].push_back(y), v[y].push_back(x);
	}
	dfs(1, 0), dfs1(ans, 0); cout << ans << " ";
	for(int i = 1; i <= n; i ++) res += sz[i];
	cout << res << "\n";
	return 0;
}