2-SAT

$\text{luogu-4782}$

有 $n$ 个布尔变量 $x_1\sim x_n$，另有 $m$ 个需要满足的条件，每个条件的形式都是「$x_i$ 为 true / false 或 $x_j$ 为 true / false」。比如「$x_1$ 为真或 $x_3$ 为假」、「$x_7$ 为假或 $x_2$ 为假」。

2-SAT 问题的目标是给每个变量赋值使得所有条件得到满足。

$1 \le n,m \le 10^6$。

什么是 2-SAT？

首先，把「2」和「SAT」拆开。SAT 是 Satisfiability 的缩写，意为可满足性。即一串布尔变量，每个变量只能为真或假。要求对这些变量进行赋值，满足布尔方程。

举个例子：教练正在讲授一个算法，代码要给教室中的多位同学阅读，代码的码风要满足所有学生。假设教室当中有三位学生：Anguei、Anfangen、Zachary_260325。现在他们每人有如下要求：

Anguei: 我要求代码当中满足下列条件之一：
1. 不写 using namespace std; （ $\neg a$）
2. 使用读入优化（$b$）
3. 大括号不换行（$\neg c$）
Anfangen: 我要求代码当中满足下条件之一：
1. 写 using namespace std; （$a$）
2. 使用读入优化（$b$）
3. 大括号不换行（$\neg c$）
Zachary_260325：我要求代码当中满足下条件之一：
1. 不写 using namespace std; （$\neg a$）
2. 使用 scanf （$\neg b$）
3. 大括号换行（$c$）

我们不妨把三种要求设为 $a,b,c$，变量前加 $\neg$ 表示「不」，即「假」。上述条件翻译成布尔方程即：$(\neg a\vee b\vee\neg c) \wedge (a\vee b\vee\neg c) \wedge (\neg a\vee\neg b\vee c)$。其中，$\vee$ 表示或，$\wedge$ 表示与。（就像集合中并集交集一样）

现在要做的是，为 ABC 三个变量赋值，满足三位学生的要求。

Q: 这可怎么赋值啊？暴力？

A: 对，这是 SAT 问题，已被证明为 NP 完全 的，只能暴力。

Q: 那么 2-SAT 是什么呢？

A: 2-SAT，即每位同学只有两个条件（比如三位同学都对大括号是否换行不做要求，这就少了一个条件）不过，仍要使所有同学得到满足。于是，以上布尔方程当中的 $c,\neg c$ 没了，变成了这个样子：$(\neg a\vee b) \wedge (a\vee b) \wedge (\neg a\vee\neg b)$

怎么求解 2-SAT 问题？

使用强连通分量。对于每个变量 $x$，我们建立两个点：$x, \neg x$ 分别表示变量 $x$ 取 true 和取 false。所以，图的节点个数是两倍的变量个数。在存储方式上，可以给第 $i$ 个变量标号为 $i$，其对应的反值标号为 $i + n$。对于每个同学的要求 $(a \vee b)$，转换为 $\neg a\rightarrow b\wedge\neg b\rightarrow a$。对于这个式子，可以理解为：「若 $a$ 假则 $b$ 必真，若 $b$ 假则 $a$ 必真」然后按照箭头的方向建有向边就好了。综上，我们这样对上面的方程建图：

原式	建图
$\neg a\vee b$	$a\rightarrow b\wedge\neg b\rightarrow\neg a$
$a \vee b$	$\neg a\rightarrow b\wedge\neg b\rightarrow a$
$\neg a\vee\neg b\space \space $	$a\rightarrow\neg b\wedge b\rightarrow\neg a$

于是我们得到了这么一张图：

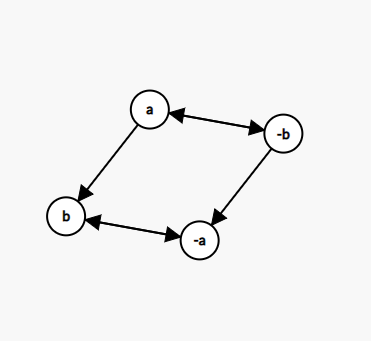
built

可以看到，$\neg a$ 与 $b$ 在同一强连通分量内，$a$ 与 $\neg b$ 在同一强连通分量内。同一强连通分量内的变量值一定是相等的。也就是说，如果 $x$ 与 $\neg x$ 在同一强连通分量内部，一定无解。反之，就一定有解了。

找解很简单，只需要 当 $x$ 所在的强连通分量的拓扑序在 $\neg x$ 所在的强连通分量的拓扑序之后取 $x$ 为真 就可以了。因为若 $x$ 在 $\neg x$ 之后，则说明 $\neg x$ 成立的话 $x$ 一定成立，矛盾，于是让 $x$ 成立。由于求强连通分量的过程中是逆向的拓扑序，所以应是 $scc_x < scc_{x+n}$。

时间复杂度为 $O(N + M)$。

#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;
#define MAXN 2000005

long long read() {
	long long x = 0, f = 1;
	char c = getchar();
	while(c > 57 || c < 48) { if(c == 45) f = -1; c = getchar(); }
	while(c >= 48 && c <= 57) { x = (x << 1) + (x << 3) + (c - 48); c = getchar(); }
	return x * f;
}

long long n, m, dfn[MAXN], low[MAXN], dn, s[MAXN], is[MAXN];
long long top, cnt, scc[MAXN];
vector<long long> v[MAXN];

void tarjan(long long x) {
	dfn[x] = low[x] = ++ dn, s[++ top] = x, is[x] = 1;
	for(auto y : v[x]) 
		if(!dfn[y]) tarjan(y), low[x] = min(low[x], low[y]);
		else if(is[y]) low[x] = min(low[x], dfn[y]);
	if(dfn[x] == low[x]) {
		cnt ++;
		do {
			scc[s[top]] = cnt, is[s[top]] = 0;
		} while(s[top --] != x);
	}
	return;
}

int main() {
	n = read(), m = read();
	for(int i = 1; i <= m; i ++) {
		long long x = read(), px = read(), y = read(), py = read();
		v[x + n * (px & 1)].push_back(y + n * (py ^ 1));
		v[y + n * (py & 1)].push_back(x + n * (px ^ 1));
	}
	for(int i = 1; i <= 2 * n; i ++) if(!dfn[i]) tarjan(i);
	for(int i = 1; i <= n; i ++) if(scc[i] == scc[i + n]) { 
		cout << "IMPOSSIBLE\n"; 
		return 0; 
	}
	cout << "POSSIBLE\n";
	for(int i = 1; i <= n; i ++)
		cout << (scc[i] < scc[i + n]) << " ";
	cout << "\n";
	return 0;
}

$\text{luogu-3209}$

若能将无向图 $G=(V, E)$ 画在平面上使得任意两条无重合顶点的边不相交，则称 $G$ 是平面图。判定一个图是否为平面图的问题是图论中的一个重要问题。现在假设你要判定的是一类特殊的图，图中存在一个包含所有顶点的环，即存在哈密顿回路，会给定哈密顿回路上的点。

$1 \le T \le 100$，$3 \le n \le 200$，$1 \le m \le 10^4$。

由于有哈密顿回路，我们钦定回路上的点编号递增，处理一下映射关系就好了。

于是每条在环上的边都可以用一个区间 $[l,r]$ 表示，这条边连接 $l,r$ 两个点。

对于两条边相交，当且仅当两条边都在环内或环外，且满足以下任意两种情况：

\[\begin{align} &[l_1, &&r_1] \\ [l_2, &&r_2] \end{align} \]

或

\[\begin{align} [l_1, &&r_1] \\ &[l_2, &&r_2] \end{align} \]

注意：任意端点一样的两个区间一定不交。

于是对于这样在同一侧会相交的边，一定需要在不同的两侧放着。

考虑用 2-SAT 刻画这个问题。

对这样的两个边编号为 $x,y$。$f_x=0$ 表示在内测，$f_x = 1$ 表示在外侧。

于是就得到了两条限制，$(f_x \vee f_y) \wedge (\neg f_x \vee \neg f_y)$，于是我们连 $4$ 条边即可。

对连边后的图跑 2-SAT，若成立则 YES，不成立则 NO。

但是这样的时间复杂度是 $O(m^2)$ 的，不可接受。

再思考一下可以发现，满足条件的情况下，边数最多是 $3n - 6$，也就是说如果 $m > 3n-6$ 一定不成立，特判一下即可。时间复杂度降至 $O(n^2)$。

#include<iostream>
#include<cstdio>
#include<vector>
#include<cstring>
using namespace std;
#define MAXN 10005

long long read() {
	long long x = 0, f = 1;
	char c = getchar();
	while(c > 57 || c < 48) { if(c == 45) f = -1; c = getchar(); }
	while(c >= 48 && c <= 57) { x = (x << 1) + (x << 3) + (c - 48); c = getchar(); }
	return x * f;
}

long long T, n, m, f[MAXN], dfn[MAXN], low[MAXN], dn, s[MAXN];
struct node { long long x, y; } e[MAXN];
long long is[MAXN], top, scc[MAXN], cnt;
vector<long long> v[MAXN];

bool check(long long l, long long r, long long L, long long R) {
	if(l < L && L < r && R > r) return true;
	if(l < R && R < r && L < l) return true;
	return false;
}

void tarjan(long long x) {
	dfn[x] = low[x] = ++ dn, s[++ top] = x, is[x] = 1;
	for(auto y : v[x]) 
		if(!dfn[y]) tarjan(y), low[x] = min(low[x], low[y]);
		else if(is[y]) low[x] = min(low[x], dfn[y]);
	if(dfn[x] == low[x]) {
		cnt ++;
		do {
			scc[s[top]] = cnt, is[s[top]] = 0;
		} while(s[top --] != x);
	}
	return;
}

int main() {
	n = read(), m = read();
	for(int i = 1; i <= m; i ++) {
		e[i].x = read(), e[i].y = read();
		if(e[i].x > e[i].y) swap(e[i].x, e[i].y);
	}
	for(int i = 1; i <= m; i ++) for(int j = i + 1; j <= m; j ++) 
		if(check(e[i].x, e[i].y, e[j].x, e[j].y)) {
			v[i + m].push_back(j), v[i].push_back(j + m);
			v[j + m].push_back(i), v[j].push_back(i + m);
		}
	for(int i = 1; i <= 2 * m; i ++) if(!dfn[i]) tarjan(i);
	bool fg = true;
	for(int i = 1; i <= m; i ++) 
		if(scc[i] == scc[i + m]) { fg = false; break; }
	if(!fg) { cout << "Impossible\n"; return 0; }
	for(int i = 1; i <= m; i ++) 
		if(scc[i] < scc[i + m]) cout << "i";
		else cout << "o";
	cout << "\n";
	return 0;
}

$\text{codeforces-27d}$

众所周知，贝兰有 $n$ 座城市，它们组成了银环——城市 $i$ 和 $i+1$（$1 \le i < n$）之间有条路相连，城市 $n$ 和 $1$ 之间也有路相连。政府决定新建 $m$ 条道路。道路清单已经准备好，每条新路都将连接两个城市。每条路都是一条曲线，要么完全在环的内侧，要么完全在外侧。新路除了端点外，不能与环上的路有任何交点。

现在设计师们想知道，能否安排这些新路，使得它们之间没有交叉（注意，路可以在端点相交）。如果可以，哪些路应该建在环的内侧，哪些路应该建在外侧呢？

$4 \le n \le 100$，$1 \le m \le 100$。

上一题的弱化版，本质上是一样的，不需要处理特判和映射关系。

需要输出一种解。

#include<iostream>
#include<cstdio>
#include<vector>
#include<cstring>
using namespace std;
#define MAXN 10005

/*跟上题一样，不贴了*/

int main() {
	n = read(), m = read();
	for(int i = 1; i <= m; i ++) {
		e[i].x = read(), e[i].y = read();
		if(e[i].x > e[i].y) swap(e[i].x, e[i].y);
	}
	for(int i = 1; i <= m; i ++) for(int j = i + 1; j <= m; j ++) 
		if(check(e[i].x, e[i].y, e[j].x, e[j].y)) {
			v[i + m].push_back(j), v[i].push_back(j + m);
			v[j + m].push_back(i), v[j].push_back(i + m);
		}
	for(int i = 1; i <= 2 * m; i ++) if(!dfn[i]) tarjan(i);
	bool fg = true;
	for(int i = 1; i <= m; i ++) 
		if(scc[i] == scc[i + m]) { fg = false; break; }
	if(!fg) { cout << "Impossible\n"; return 0; }
	for(int i = 1; i <= m; i ++) 
		if(scc[i] < scc[i + m]) cout << "i";
		else cout << "o";
	cout << "\n";
	return 0;
}

$\text{luogu-3825}$

小 L 计划进行 $n$ 场游戏，每场游戏使用一张地图，小 L 会选择一辆车在该地图上完成游戏。

小 L 的赛车有三辆，分别用大写字母 $A$、$B$、$C$ 表示。地图一共有四种，分别用小写字母 $x$、$a$、$b$、$c$ 表示。

其中，赛车 $A$ 不适合在地图 $a$ 上使用，赛车 $B$ 不适合在地图 $b$ 上使用，赛车 $C$ 不适合在地图 $c$ 上使用，而地图 $x$ 则适合所有赛车参加。

适合所有赛车参加的地图并不多见，最多只会有 $d$ 张。

$n$ 场游戏的地图可以用一个小写字母组成的字符串描述。例如：$S=\texttt{xaabxcbc}$ 表示小 L 计划进行 $8$ 场游戏，其中第 $1$ 场和第 $5$ 场的地图类型是 $x$，适合所有赛车，第 $2$ 场和第 $3$ 场的地图是 $a$，不适合赛车 $A$，第 $4$ 场和第 $7$ 场的地图是 $b$，不适合赛车 $B$，第 $6$ 场和第 $8$ 场的地图是 $c$，不适合赛车 $C$。

小 L 对游戏有一些特殊的要求，这些要求可以用四元组 $ (i, h_i, j, h_j) $ 来描述，表示若在第 $i$ 场使用型号为 $h_i$ 的车子，则第 $j$ 场游戏要使用型号为 $h_j$ 的车子。

你能帮小 L 选择每场游戏使用的赛车吗？如果有多种方案，输出任意一种方案。

如果无解，输出 -1。

$1 \le n \le 5 \times 10^4$，$0 \le d \le 8$，$1 \le m \le 10^5$。

首先考虑 $d=0$ 的情况。

那么每个点都有两种状态，$i$ 和 $\neg i$，分别表示选用这张地图可用的第一张和第二张地图。

对于每个限制条件，令 $u$ 表示”第 $i$ 场使用型号为 $h_i$ 的车“的点，$v$ 表示”第 $j$ 场使用型号为 $h_j$ 的车“的点，$\neg u$ 和 $\neg v$ 则相反。那么就会有下面三种情况：

如果第 $i$ 场不允许使用 $h_i$ 的车，则不做操作。
如果第 $i$ 场可用 $h_i$，但第 $j$ 场不允许使用 $h_j$，那么如果 $u$ 为真，则一定无解，连边 $u \to \neg u$。
如果第 $i,j$ 场都可用，则连边 $u \to v$ 和 $\neg v \to \neg u$。

建完边之后就是 2-SAT 问题，可以得到一种可行解，找不到则无解。

此时再考虑 $d \ne 0$ 的情况。

显然可以枚举 x 地图使用 A/B/C 的情况就可以得到答案。

但时间复杂度为 $O((n+m) \times 3^d)$，不可接受，考虑优化。

我们发现其实枚举两种不允许的方案即可，比如枚举 x 地图不允许 A/B：

不允许 A 的话，只能使用 B/C。
不允许 B 的话，只能使用 A/C。

实际上覆盖了三种情况，于是如果有解则一定能找到一种解，否则无解。

时间复杂度为 $O((n+m) \times 2^d)$。

注意：细节非常多，写的时候需要思路捋顺。

#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;
#define MAXN 200005

long long read() {
	long long x = 0, f = 1;
	char c = getchar();
	while(c > 57 || c < 48) { if(c == 45) f = -1; c = getchar(); }
	while(c >= 48 && c <= 57) { x = (x << 1) + (x << 3) + (c - 48); c = getchar(); }
	return x * f;
}

char get() {
    char c; while ((c = getchar()) != 'A' && c != 'B' && c != 'C');
    return c;
}

long long n, d, m, dfn[MAXN], low[MAXN], dn, s[MAXN];
struct node { long long x, y; char s, t; } e[MAXN];
long long is[MAXN], cnt, top, scc[MAXN], p[MAXN];
vector<long long> v[MAXN];
char st[MAXN], pb[MAXN];
bool fg;

void tarjan(long long x) {
	dfn[x] = low[x] = ++ dn, s[++ top] = x, is[x] = 1;
	for(auto y : v[x]) 
		if(!dfn[y]) tarjan(y), low[x] = min(low[x], low[y]);
		else if(is[y]) low[x] = min(low[x], dfn[y]);
	if(dfn[x] == low[x]) {
		cnt ++;
		do {
			scc[s[top]] = cnt, is[s[top]] = 0;
		} while(s[top --] != x);
	}
	return;
}

long long neg(long long x) { return (x > n) ? x - n : x + n; }

long long tran(long long x, char c) {
	if(st[x] == 'a') return (c == 'B') ? x : x + n;
	if(st[x] == 'b' || st[x] == 'c') return (c == 'A') ? x : x + n;
	return (c == 'C') ? x + n : x;
}

bool solve() {
	for(int i = 1; i <= 2 * n; i ++) dfn[i] = 0, v[i].clear();
	for(int i = 1; i <= m; i ++) 
		if(s[e[i].x] != 'x' && st[e[i].y] != 'x') {
			if(e[i].s - 'A' == st[e[i].x] - 'a') continue;
			long long x = tran(e[i].x, e[i].s), y;
			if(e[i].t - 'A' == st[e[i].y] - 'a') {
				v[x].push_back(neg(x)); continue;
			}
			y = tran(e[i].y, e[i].t);
			v[x].push_back(y), v[neg(y)].push_back(neg(x));
		}
		else {
			char cx = st[e[i].x], cy = st[e[i].y];
			long long x, y, px = p[e[i].x], py = p[e[i].y];
			if(cx == 'x' && cy == 'x') {
				if(e[i].s == pb[px]) continue;
				x = tran(e[i].x, e[i].s);
				if(e[i].t == pb[py]) {
					v[x].push_back(neg(x)); continue;
				}
				y = tran(e[i].y, e[i].t);
				v[x].push_back(y), v[neg(y)].push_back(neg(x));
			}
			else if(cx == 'x' && cy != 'x') {
				if(e[i].s == pb[px]) continue;
				x = tran(e[i].x, e[i].s);
				if(e[i].t - 'A' == st[e[i].y] - 'a') {
					v[x].push_back(neg(x)); continue;
				}
				y = tran(e[i].y, e[i].t);
				v[x].push_back(y), v[neg(y)].push_back(neg(x));
			}
			else {
				if(e[i].s - 'A' == st[e[i].x] - 'a') continue;
				x = tran(e[i].x, e[i].s);
				if(e[i].t == pb[py]) {
					v[x].push_back(neg(x)); continue;
				}
				y = tran(e[i].y, e[i].t);
				v[x].push_back(y), v[neg(y)].push_back(neg(x));
			}
		}
	for(int i = 1; i <= 2 * n; i ++) if(!dfn[i]) tarjan(i);
	for(int i = 1; i <= n; i ++) if(scc[i] == scc[i + n]) return 0;
	for(int i = 1; i <= n; i ++) 
		if(scc[i] < scc[i + n])
			if(st[i] == 'a') cout << "B";
			else if(st[i] == 'b' || st[i] == 'c') cout << "A";
			else if(pb[p[i]] == 'A') cout << "B";
			else cout << "A";
		else {
			if(st[i] == 'a' || st[i] == 'b') cout << "C";
			else if(st[i] == 'c') cout << "B";
			else if(pb[p[i]] == 'A') cout << "C";
			else cout << "B"; 
		}
	cout << "\n";
	return 1;
}

void dfs(long long x) {
	if(fg) return; 
	if(x > d) { fg = solve(); return; }
	pb[x] = 'A', dfs(x + 1);
	pb[x] = 'B', dfs(x + 1);
	return;
}

int main() {
	n = read(), read(); cin >> (st + 1); m = read();
	for(int i = 1; i <= n; i ++) if(st[i] == 'x') p[i] = ++ d;
	for(int i = 1; i <= m; i ++) 
		e[i].x = read(), e[i].s = get(), e[i].y = read(), e[i].t = get();
	dfs(1); if(!fg) cout << "-1";
	return 0;
}

$\text{loj-10097 / luogu-5782}$

根据宪法，Byteland 民主共和国的公众和平委员会应该在国会中通过立法程序来创立。不幸的是，由于某些党派代表之间的不和睦而使得这件事存在障碍。此委员会必须满足下列条件：

每个党派都在委员会中恰有 $1$ 个代表。
如果 $2$ 个代表彼此厌恶，则他们不能都属于委员会。

每个党在议会中有 $2$ 个代表。代表从 $1$ 编号到 $2n$。编号为 $2i-1$ 和 $2i$ 的代表属于第 $i$ 个党派。

任务：写一程序读入党派的数量和关系不友好的代表对，计算决定建立和平委员会是否可能，若行，则列出委员会的成员表。

$1 \leq n \leq 8000$，$0 \leq m \leq 20000$，$1 \leq a < b \leq 8000$。

考虑刻画为 2-SAT 问题，若 $i,i+1$ 是一个党派的，分别记为 $i,\neg i$。

若 $x,y$ 互相厌恶，则有 $x \to \neg y, y \to \neg x$ 两条边。

之后跑 2-SAT 就好了。

#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;
#define MAXN 50005

long long read() {
	long long x = 0, f = 1;
	char c = getchar();
	while(c > 57 || c < 48) { if(c == 45) f = -1; c = getchar(); }
	while(c >= 48 && c <= 57) { x = (x << 1) + (x << 3) + (c - 48); c = getchar(); }
	return x * f;
}

long long n, m, dfn[MAXN], low[MAXN], dn, s[MAXN], is[MAXN];
long long top, cnt, scc[MAXN];
vector<long long> v[MAXN];

void tarjan(long long x) {
	dfn[x] = low[x] = ++ dn, s[++ top] = x, is[x] = 1;
	for(auto y : v[x]) 
		if(!dfn[y]) tarjan(y), low[x] = min(low[x], low[y]);
		else if(is[y]) low[x] = min(low[x], dfn[y]);
	if(dfn[x] == low[x]) {
		cnt ++;
		do {
			scc[s[top]] = cnt, is[s[top]] = 0;
		} while(s[top --] != x);
	}
	return;
}

long long neg(long long x) { return (x % 2) ? x + 1 : x - 1; }

int main() {
	n = read(), m = read();
	for(int i = 1; i <= m; i ++) {
		long long x = read(), y = read();
		v[x].push_back(neg(y));
		v[y].push_back(neg(x));
	}
	for(int i = 1; i <= 2 * n; i ++) if(!dfn[i]) tarjan(i);
	for(int i = 1; i <= 2 * n; i += 2)
		if(scc[i] == scc[i + 1]) { cout << "NIE\n"; return 0; }
	for(int i = 1; i <= 2 * n; i += 2) 
		if(scc[i] < scc[i + 1]) cout << i << "\n";
		else cout << i + 1 << "\n";
	return 0;
}

posted @ 2026-01-07 21:19 So_noSlack 阅读(3) 评论(0) 收藏举报

刷新页面返回顶部

原式	建图
\(\neg a\vee b\)	\(a\rightarrow b\wedge\neg b\rightarrow\neg a\)
\(a \vee b\)	\(\neg a\rightarrow b\wedge\neg b\rightarrow a\)
$\neg a\vee\neg b\space \space $	\(a\rightarrow\neg b\wedge b\rightarrow\neg a\)

So_noSlack 的博客

2-SAT

\(\text{luogu-4782}\)

\(\text{luogu-3209}\)

\(\text{codeforces-27d}\)

\(\text{luogu-3825}\)

\(\text{loj-10097 / luogu-5782}\)

公告