摘要：
费马小定理：若 \(p\) 为质数，则 \(x^{p}\equiv x(\text{mod}\ p)\)。特别地，若 \(p\not\mid x\)，则 \(x^{p-1}\equiv 1(\text{mod}\ p)\)。 首先，若 \(p\mid x\)，则 \(x\equiv 0(\text{ 阅读全文
posted @ 2025-10-06 22:03
SigmaToT
阅读(23)
评论(0)
推荐(0)
摘要：
威尔逊定理： 首先，对于 \(p = 2\)，显然成立。 若 \(p \not= 2\)，我们考虑一个 \(x\) 在模 \(p\) 意义下的逆元若是他自己，则 \(x^2\equiv 1(\text{mod}\ p)\)。 \(x\equiv 1\) 或 \(p - 1(\text{mod}\ p 阅读全文
posted @ 2025-10-06 21:42
SigmaToT
阅读(26)
评论(0)
推荐(0)
摘要：
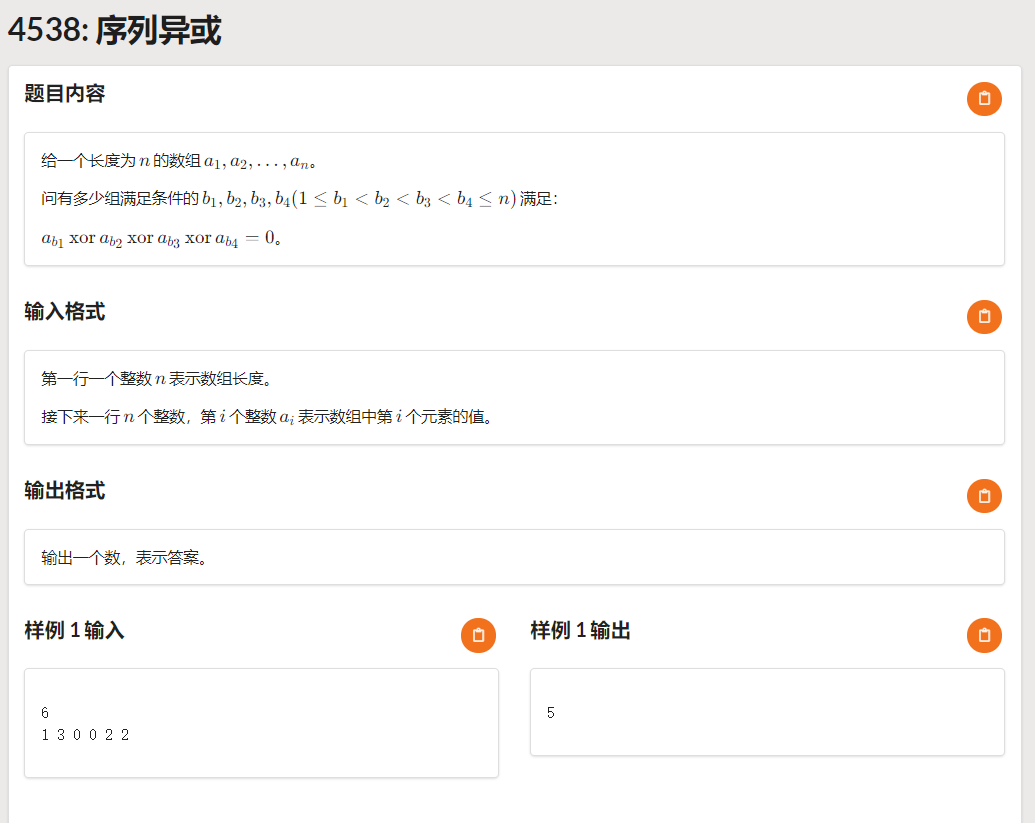
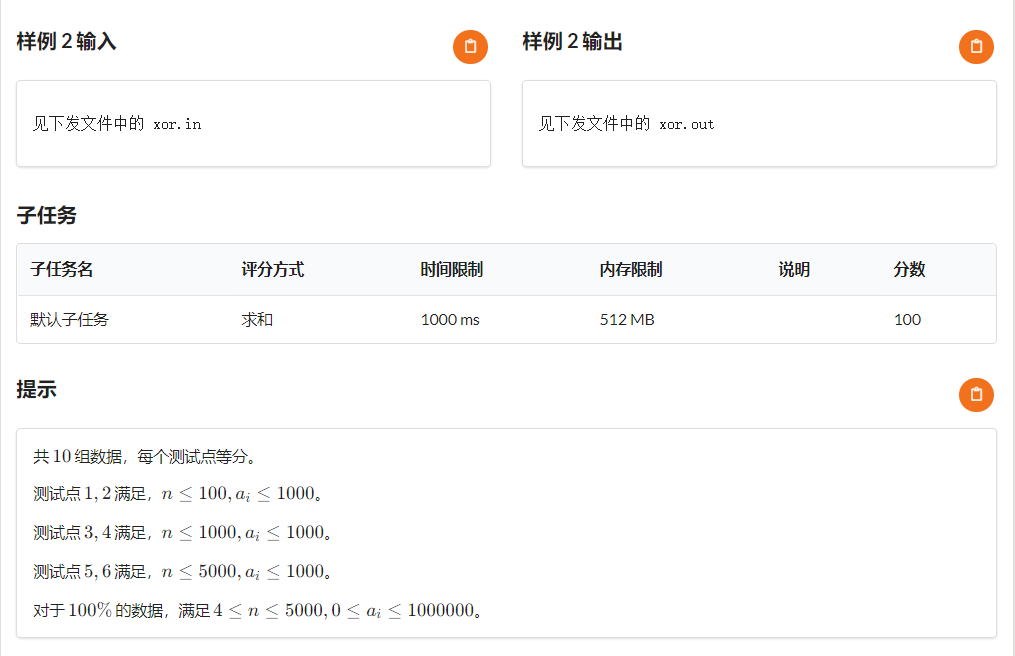
今天更废了。 \(30pts\ rk84\)。 今天的题 T1 机房大部分人都做出来了，可是我只是打了个暴力（还没拿分）。 这道题其实可以把 \((b_1,b_2,b_3,b_4)\) 分为 \((b_1,b_2),(b_3,b_4)\) 两个部分。 这样的话，我们就可以开一个桶，然后存 \(a_{ 阅读全文
posted @ 2025-10-06 21:18
SigmaToT
阅读(8)
评论(0)
推荐(0)
摘要：
我们要估算 \(\displaystyle\sum^n_{i = 1}\dfrac{1}{i}\)。 我们知道 \(\displaystyle\sum^n_{i = 1}\dfrac{1}{i}\approx \int_1^n\dfrac{1}{i} = (\ln\left|i\right|)\bi 阅读全文
posted @ 2025-10-06 16:37
SigmaToT
阅读(38)
评论(0)
推荐(0)
摘要：
阶：满足 \(x^{k}\equiv 1(\text{mod}\ p)\) 的最小 \(k\)。 首先，若 \(x\not\perp p\)，则无解。 令 \(f(k) = x^k\mod p\) 若有解，则由费马小定理知，\(k = p - 1\) 是 \(f(x) = 1\) 的一个解。 令其最 阅读全文
posted @ 2025-10-06 16:19
SigmaToT
阅读(7)
评论(0)
推荐(0)
摘要：
\(a\cdot a^{-1}\equiv 1(\text{mod}\ p)\)。 我们要求 \(a^{-1}\)。 设 \(p = ma + n\)，\(1 \leq n \leq a - 1\)。 所以 \(ma + n\equiv 0(\text{mod}\ p)\) 两边同时乘以 \(a^{ 阅读全文
posted @ 2025-10-06 16:02
SigmaToT
阅读(15)
评论(0)
推荐(0)
摘要：
  
浙公网安备 33010602011771号