字符串(集训2025.7.18)笔记
由于一直在做题,所以前面的笔记没来得及写。
老师的课件:https://files.cnblogs.com/files/blogs/832279/字符串基础part1.rar?t=1752841854&download=true
我似乎只做出来了这一道新题:星战
P8819 [CSP-S 2022] 星战
题目描述
在这一轮的星际战争中,我方在宇宙中建立了 \(n\) 个据点,以 \(m\) 个单向虫洞连接。我们把终点为据点 \(u\) 的所有虫洞归为据点 \(u\) 的虫洞。
战火纷飞之中这些虫洞很难长久存在,敌人的打击随时可能到来。这些打击中的有效打击可以分为两类:
- 敌人会摧毁某个虫洞,这会使它连接的两个据点无法再通过这个虫洞直接到达,但这样的打击无法摧毁它连接的两个据点。
- 敌人会摧毁某个据点,由于虫洞的主要技术集中在出口处,这会导致该据点的所有还未被摧毁的虫洞被一同摧毁。而从这个据点出发的虫洞则不会摧毁。
注意:摧毁只会导致虫洞不可用,而不会消除它的存在。
为了抗击敌人并维护各部队和各据点之间的联系,我方发展出了两种特种部队负责修复虫洞:
- A 型特种部队则可以将某个特定的虫洞修复。
- B 型特种部队可以将某据点的所有损坏的虫洞修复。
考虑到敌人打击的特点,我方并未在据点上储备过多的战略物资。因此只要这个据点的某一条虫洞被修复,处于可用状态,那么这个据点也是可用的。
我方掌握了一种苛刻的空间特性,利用这一特性我方战舰可以沿着虫洞瞬移到敌方阵营,实现精确打击。
为了把握发动反攻的最佳时机,指挥部必须关注战场上的所有变化,为了寻找一个能够进行反攻的时刻。总指挥认为:
- 如果从我方的任何据点出发,在选择了合适的路线的前提下,可以进行无限次的虫洞穿梭(可以多次经过同一据点或同一虫洞),那么这个据点就可以实现反击。
- 为了使虫洞穿梭的过程连续,尽量减少战舰在据点切换虫洞时的质能损耗,当且仅当只有一个从该据点出发的虫洞可用时,这个据点可以实现连续穿梭。
- 如果我方所有据点都可以实现反击,也都可以实现连续穿梭,那么这个时刻就是一个绝佳的反攻时刻。
总司令为你下达命令,要求你根据战场上实时反馈的信息,迅速告诉他当前的时刻是否能够进行一次反攻。
输入格式
输入的第一行包含两个正整数 \(n,m\)。
接下来 \(m\) 行每行两个数 \(u,v\),表示一个从据点 \(u\) 出发到据点 \(v\) 的虫洞。保证 \(u \ne v\),保证不会有两条相同的虫洞。初始时所有的虫洞和据点都是完好的。
接下来一行一个正整数 \(q\) 表示询问个数。
接下来 \(q\) 行每行表示一次询问或操作。首先读入一个正整数 \(t\) 表示指令类型:
- 若 \(t = 1\),接下来两个整数 \(u, v\) 表示敌人摧毁了从据点 \(u\) 出发到据点 \(v\) 的虫洞。保证该虫洞存在且未被摧毁。
- 若 \(t = 2\),接下来一个整数 \(u\) 表示敌人摧毁了据点 \(u\)。如果该据点的虫洞已全部被摧毁,那么这次袭击不会有任何效果。
- 若 \(t = 3\),接下来两个整数 \(u, v\) 表示我方修复了从据点 \(u\) 出发到据点 \(v\) 的虫洞。保证该虫洞存在且被摧毁。
- 若 \(t = 4\),接下来一个整数 \(u\) 表示我方修复了据点 \(u\)。如果该据点没有被摧毁的虫洞,那么这次修复不会有任何效果。
在每次指令执行之后,你需要判断能否进行一次反攻。如果能则输出 YES 否则输出 NO。
输出格式
输出一共 \(q\) 行。对于每个指令,输出这个指令执行后能否进行反攻。
输入输出样例 #1
输入 #1
3 6
2 3
2 1
1 2
1 3
3 1
3 2
11
1 3 2
1 2 3
1 1 3
1 1 2
3 1 3
3 3 2
2 3
1 3 1
3 1 3
4 2
1 3 2
输出 #1
NO
NO
YES
NO
YES
NO
NO
NO
YES
NO
NO
说明/提示
【样例解释 #1】
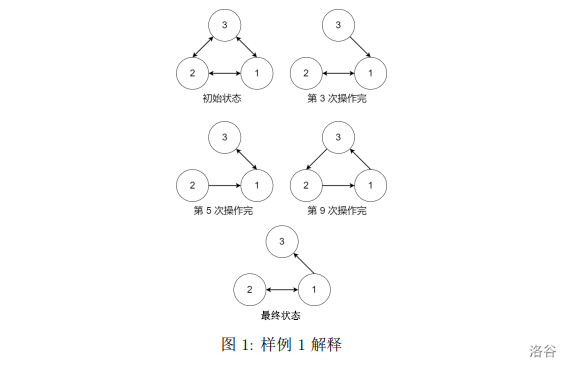
虫洞状态可以参考下面的图片, 图中的边表示存在且未被摧毁的虫洞:
【样例 #2】
见附件中的 galaxy/galaxy2.in 与 galaxy/galaxy2.ans。
【样例 #3】
见附件中的 galaxy/galaxy3.in 与 galaxy/galaxy3.ans。
【样例 #4】
见附件中的 galaxy/galaxy4.in 与 galaxy/galaxy4.ans。
【数据范围】
对于所有数据保证:\(1 \le n \le 5 \times {10}^5\),\(1 \le m \le 5 \times {10}^5\),\(1 \le q \le 5 \times {10}^5\)。
| 测试点 | \(n \le\) | \(m \le\) | \(q \le\) | 特殊限制 |
|---|---|---|---|---|
| \(1 \sim 3\) | \(10\) | \(20\) | \(50\) | 无 |
| \(4 \sim 8\) | \({10}^3\) | \({10}^4\) | \({10}^3\) | 无 |
| \(9 \sim 10\) | \(5 \times {10}^5\) | \(5 \times {10}^5\) | \(5 \times {10}^5\) | 保证没有 \(t = 2\) 和 \(t = 4\) 的情况 |
| \(11 \sim 12\) | \(5 \times {10}^5\) | \(5 \times {10}^5\) | \(5 \times {10}^5\) | 保证没有 \(t = 4\) 的情况 |
| \(13 \sim 16\) | \({10}^5\) | \(5 \times {10}^5\) | \(5 \times {10}^5\) | 无 |
| \(17 \sim 20\) | \(5 \times {10}^5\) | \(5\times 10^5\) | \(5 \times {10}^5\) | 无 |
这道题只需要记录每个点的出度,判断是不是都是 1 就行。
但是这是 \(\mathcal O(n)\) 的。
所以我们可以用哈希判断,看原序列的哈希值是否和全是 1 的序列的哈希值相同就行了。
点击查看代码
#include <iostream>
#include <vector>
#define int long long
using std::cin;
using std::cout;
const int N = 5e5 + 10;
const int mod = 1e9 + 993;
const int p = 31;
int mul[N];
int hash_g;
int hash_all_one;
int delete_val[N];
int out_degree[N];
int already_delete[N];
std::vector<int> e[N];
signed main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= m; ++i)
{
int u, v;
cin >> u >> v;
out_degree[u]++;
e[v].push_back(u);
}
mul[0] = 1;
for (int i = 1; i <= n; ++i)
mul[i] = 1ll * mul[i - 1] * p % mod;
for (int i = 1; i <= n; ++i)
hash_g = (hash_g + 1ll * out_degree[i] * mul[i] % mod) % mod;
for (int i = 1; i <= n; ++i)
hash_all_one = (hash_all_one + 1ll * mul[i]) % mod;
for (int x = 1; x <= n; ++x)
for (auto to : e[x])
delete_val[x] = (delete_val[x] + 1ll * mul[to]) % mod;
int q;
cin >> q;
while (q--)
{
int t;
cin >> t;
if (t == 1)
{
int u, v;
cin >> u >> v;
hash_g = (hash_g - mul[u] + mod) % mod;
already_delete[v] = (1ll * already_delete[v] + mul[u]) % mod;
}
else if (t == 2)
{
int u;
cin >> u;
hash_g = (hash_g - (delete_val[u] - already_delete[u] + mod) % mod + mod) % mod;
already_delete[u] = delete_val[u];
}
else if (t == 3)
{
int u, v;
cin >> u >> v;
hash_g = (1ll * hash_g + mul[u]) % mod;
already_delete[v] = (already_delete[v] - mul[u] + mod) % mod;
}
else
{
int u;
cin >> u;
hash_g = (1ll * hash_g + already_delete[u]) % mod;
already_delete[u] = 0;
}
if (hash_g == hash_all_one)
cout << "YES" << '\n';
else
cout << "NO" << '\n';
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号