2025.7.14笔记

ST 表

一般很少写。
一般用来很快求LCA。

LCA

1.

先转化成欧拉序。
记录每个点的深度，并记录每个欧拉序对应的数组下标。
写一个ST表，假设要查询 \(l\sim r\)，就查询 \(l\sim r\) 中深度最小对应的点。

点击查看代码 
#include <vector>
#include <iostream>

using std::cin;
using std::cout;
const int N = 1e6 + 10;

int cnt;
int dep[N];
int lg2[N];
int ett[N];
int pos[N]; // i 节点在 ett 中任意一个出现位置 
int f[N][23];
int ly[N][23]; // 最小值的来源（是哪个点） 
std::vector<int> e[N];

void init(int x, int fa)
{
	dep[x] = dep[fa] + 1;
	ett[++cnt] = x;
	pos[x] = cnt;
	for (auto to : e[x])
		if (to != fa)
			init(to, x), ett[++cnt] = x;
}
void build()
{
	lg2[1] = 0;
	for (int i = 2; i <= cnt; ++i)
		lg2[i] = lg2[i >> 1] + 1;
	for (int i = 1; i <= lg2[cnt]; ++i)
	{
		for (int j = 1; j <= cnt - (1 << i) + 1; ++j)
		{
			if (f[j][i - 1] < f[j + (1 << (i - 1))][i - 1])
			{
				f[j][i] = f[j][i - 1];
				ly[j][i] = ly[j][i - 1];
			}
			else
			{
				f[j][i] = f[j + (1 << (i - 1))][i - 1];
				ly[j][i] = ly[j + (1 << (i - 1))][i - 1];
			}
		}
	}
}
void init_st()
{
	for (int i = 1; i <= cnt; ++i)
	{
		ly[i][0] = ett[i];
		f[i][0] = dep[ett[i]];
	}
	build();
}
int query(int u, int v)
{
	int l = pos[u];
	int r = pos[v];
	if (l > r)
		std::swap(l, r);
	int di = lg2[r - l + 1];
	if (f[l][di] < f[r - (1 << di) + 1][di])
		return ly[l][di];
	else
		return ly[r - (1 << di) + 1][di];
}

int main()
{
	int n, m, rt;
	std::cin >> n >> m >> rt;
	for (int i = 1; i <= n - 1; ++i)
	{
		int u, v;
		std::cin >> u >> v;
		e[u].push_back(v);
		e[v].push_back(u);
	}
	init(rt, 0);
	init_st();
	for (int i = 1; i <= m; ++i)
	{
		int u, v;
		std::cin >> u >> v;
		std::cout << query(u, v) << '\n';
	}
	return 0;
}

代码又臭又长。

2.

喜闻乐见的倍增。
直接放代码。

点击查看代码 
#include <vector>
#include <iostream>

using std::cin;
using std::cout;
const int N = 1e6 + 10;

int n;
int m;
int lg2[N];
int dep[N];
int f[N][23];
std::vector<int> e[N];

void dfs(int x, int fa)
{
	dep[x] = dep[fa] + 1;
	f[x][0] = fa;
	for (int i = 1; i <= lg2[dep[x]]; ++i)
		f[x][i] = f[f[x][i - 1]][i - 1];
	for (auto to : e[x])
		if (to != fa)
			dfs(to, x);
}
void build()
{
	lg2[1] = 0;
	for (int i = 2; i <= n; ++i)
		lg2[i] = lg2[i >> 1] + 1;
}
int query(int x, int y)
{
	if (dep[x] < dep[y])
		std::swap(x, y);
	int d = dep[x] - dep[y];
	for (int i = 0; i <= lg2[d]; ++i)
		if ((1 << i) & d)
			x = f[x][i];
	if (x == y)
		return x;
	for (int i = lg2[n]; i >= 0; --i)
		if (f[x][i] ^ f[y][i] && f[x][i] && f[y][i])
			x = f[x][i], y = f[y][i];
	return f[x][0];
}

int main()
{
	int rt;
	cin >> n >> m >> rt;
	for (int i = 1; i < n; ++i)
	{
		int u, v;
		cin >> u >> v;
		e[u].push_back(v);
		e[v].push_back(u);
	}
	build();
	dfs(rt, 0);
	for (int i = 1; i <= m; ++i)
	{
		int u, v;
		cin >> u >> v;
		cout << query(u, v) << '\n';
	}
	return 0;
}

并查集

不用记。

线段树

维护最大子段和、最大前缀、最大后缀、总和。

小白逛公园

点击查看代码 
#include <iostream>
#include <algorithm>

using std::cin;
using std::cout;
using std::max;
using std::min;
const int N = 5e5 + 10;
typedef long long ll;

struct Node
{
	ll sum;
	ll max_pre;
	ll max_suff;
	ll max_sum;
	Node()
	{
		sum = max_pre = max_suff = max_sum = 0;
	}
	void init(int v)
	{
		sum = max_pre = max_suff = max_sum = v;
		// max_pre = max(max_pre, 0);
		// max_suff = max(max_suff, 0);
		// max_sum = max(max_sum, 0);
	}
	friend Node operator+(const Node &a, const Node &b)
	{
		Node ret;
		ret.sum = a.sum + b.sum;
		ret.max_pre = max(a.max_pre, a.sum + b.max_pre);
		ret.max_suff = max(b.max_suff, b.sum + a.max_suff);
		ret.max_sum = max(max(a.max_sum, b.max_sum), a.max_suff + b.max_pre);
		return ret;
	}
} z[N << 2];

ll a[N];

#define root 1, n, 1
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1

void build(int l, int r, int rt)
{
	if (l == r)
	{
		z[rt].init(a[l]);
		return;
	}
	int m = (l + r) >> 1;
	build(lson);
	build(rson);
	z[rt] = z[rt << 1] + z[rt << 1 | 1];
}
void modify(int l, int r, int rt, int p, ll k)
{
	if (l == r)
	{
		z[rt].init(k);
		return;
	}
	int m = (l + r) >> 1;
	if (p <= m)
		modify(lson, p, k);
	else
		modify(rson, p, k);
	z[rt] = z[rt << 1] + z[rt << 1 | 1];
}
Node query(int l, int r, int rt, int nowl, int nowr)
{
	if (nowl <= l && r <= nowr)
		return z[rt];
	int m = (l + r) >> 1;
	if (nowl <= m)
	{
		if (nowr > m)
			return query(lson, nowl, nowr) + query(rson, nowl, nowr);
		else
			return query(lson, nowl, nowr);
	}
	else
		return query(rson, nowl, nowr);
}

int main()
{
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= n; ++i)
		cin >> a[i];
	build(root);
	while (m--)
	{
		int k, a, b;
		cin >> k >> a >> b;
		if (k == 1)
		{
			if (a > b)
				std::swap(a, b);
			cout << query(root, a, b).max_sum << '\n';
		}
		else
			modify(root, a, b);
	}
	return 0;
}

方差

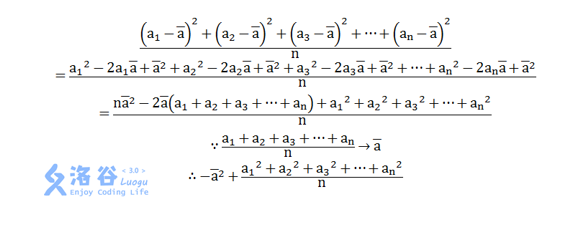
image

直接维护。

点击查看代码 
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>

using namespace std;
const int N = 20000005;
typedef long long ll;

int n, m;
double a[N];
double sq[N];
double sum[N << 2];
double mx[N << 2];
double tag[N];

int ls(int x)
{
  return x << 1;
}
int rs(int x)
{
  return x << 1 | 1;
}
void pushup(int x)
{
  sum[x] = sum[ls(x)] + sum[rs(x)];
  sq[x] = sq[ls(x)] + sq[rs(x)];
}
void add(int x, int l, int r, double k)
{
  sq[x] += 2 * k * sum[x] + k * k * (r - l + 1);
  sum[x] += k * (r - l + 1);
  tag[x] += k;
}
void pushdown(int x, int l, int r)
{
  int mid = (l + r) >> 1;
  if (tag[x] != 0)
  {
    add(ls(x), l, mid, tag[x]);
    add(rs(x), mid + 1, r, tag[x]);
    tag[x] = 0;
  }
}
void build(int x, int l, int r)
{
  tag[x]=0;
  if (l == r)
  {
    sum[x] = a[l];
    sq[x] = a[l] * a[l];
    return;
  }
  int mid = (l + r) >> 1;
  build(ls(x), l, mid);
  build(rs(x), mid + 1, r);
  pushup(x);
}
double query_sum(int x, int l, int r, int L, int R)
{
  if (L <= l && r <= R)
    return sum[x];
  pushdown(x, l, r);
  double ret = 0;
  int mid = (l + r) >> 1;
  if (L <= mid)
  {
    ret += query_sum(ls(x), l, mid, L, R);
  }
  if (mid < R)
  {
    ret += query_sum(rs(x), mid + 1, r, L, R);
  }
  return ret;
}
double query_ll(int x, int l, int r, int L, int R)
{
  if (L <= l && r <= R)
    return sq[x];
  pushdown(x, l, r);
  double ret = 0;
  int mid = (l + r) >> 1;
  if (L <= mid)
  {
    ret += query_ll(ls(x), l, mid, L, R);
  }
  if (mid < R)
  {
    ret += query_ll(rs(x), mid + 1, r, L, R);
  }
  return ret;
}
void add_one(int x, int l, int r, int p, double k)
{
  if (l == r)
  {
    sum[x] += k;
    return;
  }
  pushdown(x, l, r);
  int mid = (l + r) >> 1;
  if (p <= mid)
    add_one(ls(x), l, mid, p, k);
  else
    add_one(rs(x), mid + 1, r, p, k);
  pushup(x);
}
void add_many(int x, int l, int r, int L, int R, double k)
{
  if (L <= l && R >= r)
  {
    add(x, l, r, k);
    return;
  }
  pushdown(x, l, r);
  int mid = (l + r) >> 1;
  if (L <= mid)
    add_many(ls(x), l, mid, L, R, k);
  if (mid < R)
    add_many(rs(x), mid + 1, r, L, R, k);
  pushup(x);
}

int main()
{
  cin >> n >> m;
  for (int i = 1; i <= n; ++i)
  {
    cin >> a[i];
  }
  build(1, 1, n);
  while (m--)
  {
    int opt;
    cin >> opt;
    if (opt == 1)
    {
      int x, y;
      double k;
      cin >> x >> y >> k;
      add_many(1, 1, n, x, y, k);
    }
    if (opt == 2)
    {
      int x, y;
      cin >> x >> y;
      printf("%.4lf\n", query_sum(1, 1, n, x, y) * 1.0 / (y - x + 1));
    }
    if (opt == 3)
    {
      int x, y;
      cin >> x >> y;
      double xx = (query_sum(1, 1, n, x, y) / (y - x + 1)) ;
      double yy = query_ll(1, 1, n, x, y) / (y - x + 1);
      printf("%.4lf\n", yy - xx * xx);
    }
  }
  return 0;
}

无名

image
image

#include <iostream>
#define int long long

using std::cin;
using std::cout;
typedef long long ll;
const int N = 1e5 + 10;
const int mod = 1e9 + 7;

struct Node
{
	ll sum;
	ll val1;
	ll val2;
	ll l, r;
	void init(ll v)
	{
		l = r = v % mod;
		sum = v % mod;
		val1 = val2 = 0;
	}
	friend Node operator+(const Node &a, const Node &b)
	{
		Node ret;
		ret.l = a.l;
		ret.r = b.r;
		ret.sum = (a.sum % mod + b.sum % mod + 2 * mod) % mod;
		ret.val1 = (a.val1 % mod + mod + b.val1 % mod + mod + a.sum * b.sum % mod + mod) % mod;
		ret.val2 = (a.val2 % mod + mod + b.val2 % mod + mod + a.r * b.l % mod + mod) % mod;
		return ret;
	}
}z[N << 2];

#define root 1, n, 1
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1

ll a[N];

void build(int l, int r, int rt)
{
	if (l == r)
	{
		z[rt].init(a[l]);
		return;
	}
	int m = (l + r) >> 1;
	build(lson);
	build(rson);
	z[rt] = z[rt << 1] + z[rt << 1 | 1];
}
void modify(int l, int r, int rt, int p, ll k)
{
	if (l == r)
	{
		z[rt].init(k);
		return;
	}
	int m = (l + r) >> 1;
	if (p <= m)
		modify(lson, p, k);
	else
		modify(rson, p, k);
	z[rt] = z[rt << 1] + z[rt << 1 | 1];
}
Node query(int l, int r, int rt, int nowl, int nowr)
{
	if (nowl <= l && r <= nowr)
		return z[rt];
	int m = (l + r) >> 1;
	if (nowl <= m)
	{
		if (nowr > m)
			return query(lson, nowl, nowr) + query(rson, nowl, nowr);
		else
			return query(lson, nowl, nowr);
	}
	else
		return query(rson, nowl, nowr);
}

signed main()
{
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= n; ++i)
		cin >> a[i], a[i] = (a[i] % mod + mod) % mod;
	build(root);
	while (m--)
	{
		char opt;
		cin >> opt;
		int x;
		ll y;
		cin >> x >> y;
		y = (y % mod + mod) % mod;
		if (opt == 'M')
			modify(root, x, y);
		else if (opt == 'Q')
			cout << query(root, x, y).val1 << '\n';
		else if (opt == 'A')
			cout << query(root, x, y).val2 << '\n';
	}
	return 0;
}

括号修复

假设我们把这个序列能消掉的都消掉了，那么一定是 \(l\) 个 ) \(+\) \(r\) 个 (。
query 答案就是 \(\left\lceil\dfrac{l}{2}\right\rceil + \left\lceil\dfrac{r}{2}\right\rceil\)。
image
其中 swap 操作需要平衡树。

火星人

假设不单点插入（因为需要平衡树）。
如何判断两（liáng）个字符串是否相等？
哈希。
LCP？
二分答案一个区间长度。
线段树查询check是否相同就可以。
复杂度 \(\mathcal O(n\log^2n)\)

线段树+暴力

1.

image
image

2.

image
image

3.

image
image

4.

image
image

5.

image
image

6.

image
image
image
image
image
image
image
image
image

7.

image
image
image
image

8.

image
image
image

posted @ 2025-07-14 15:15  SigmaToT  阅读(8)  评论(0)    收藏  举报