2025.5.3笔记
如果我有写错或令人不理解的地方,请及时指出,谢谢!!!
DP!!!

定状态(没听。。。)
\(fib\) 数列
复杂度 \(\mathcal O(n)\)
通项公式:\(f_i = \dfrac{(\dfrac{1 + \sqrt{5}}{2})^i - (\dfrac{1 - \sqrt{5}}{2})^i}{\sqrt{5}}\)
优化:矩阵快速幂。
复杂度 \(\mathcal O(\log n)\)
。。。还是远古码风。
点击查看代码
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#define int long long
using namespace std;
const int mod = 1e9 + 7;
int n;
long long k;
struct node
{
int a[3][3];
void bb()
{
a[1][1] = a[2][2] = 1;
a[1][2] = a[2][1] = 0;
}
} m;
node operator*(const node &a, const node &b)
{
node ret;
for (int i = 1; i <= 2; ++i)
{
for (int j = 1; j <= 2; ++j)
{
ret.a[i][j] = 0;
}
}
for (int i = 1; i <= 2; ++i)
{
for (int k = 1; k <= 2; ++k)
{
for (int j = 1; j <= 2; ++j)
{
ret.a[i][j] += 1ll * a.a[i][k] * b.a[k][j] % mod;
ret.a[i][j] %= mod;
}
}
}
return ret;
}
node ksm(node a, long long k)
{
node ret;
ret.bb();
for (; k; k >>= 1, a = a * a)
if (k & 1)
ret = ret * a;
return ret;
}
node ret;
signed main()
{
memset(m.a, 0, sizeof (m.a));
cin >> n;
if (n == 1)
{
cout << 1 << '\n';
return 0;
}
if (n == 2)
{
cout << 1 << '\n';
return 0;
}
m.a[1][1] = m.a[1][2] = m.a[2][1] = 1;
m.a[2][2] = 0;
n--;
ret = ksm(m, n - 1);
cout << (ret.a[1][1] + ret.a[1][2]) % mod;
return 0;
}
注意:矩阵乘法的循环把 \(j\) 放在最后是最快的。
原理:
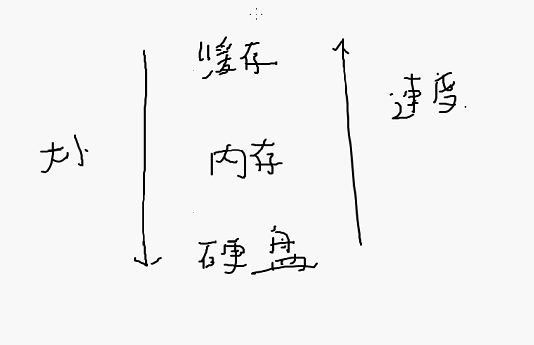

最后枚举 \(j\) 很多次都在同一行读取。
读取速度能差 \(100\) 倍。
从小到大枚举比从大到小枚举快。
矩阵乘法优化

\(f\)\([\)走了几步\(]\)\([\)位置\(]\) \(=\) 方案数
\(f[i][j] = \displaystyle\sum^n_{k = 1}f[i - 1][k]\cdot M[k][j]\)
\(t\leq 10^9\)
一旦看到转移式子长成这样,就是矩阵乘法。
1.升维:\(f[i][1][j] = \displaystyle\sum^n_{k = 1}f[i - 1][1][k]\cdot M[k][j]\)
2.降维:把 \(f_i\) 和 \(f_{i - 1}\) 当成两个二维数组。
\(f_i[1][j] = \displaystyle\sum^n_{k = 1}f_{i - 1}[1][k]\cdot M[k][j]\)
就有了矩阵乘法的形式, \(f_i = f_{i - 1}\cdot M\)。
\(f_t = f_0\cdot M^t\),\(f[0][1] = 1 \to f_0[1][1] = 1\)
答案即为 \(f_t.a[1][n]\)。
这类 DP 的特征:
1.从 \(i - 1\) 转移到 \(i\)。
2.转移系数 \(M\) 与 \(i\) 无关。
例1
边有长度,因此拆边,转化成上一个问题。
但会有 \(700\) 多个点,会超时。

让它们共享几条边。
这样每一个点只会伸出最多 \(90\) 个点。
点击查看代码
#include <iostream>
#include <cstring>
using std::cin;
using std::cout;
const int N = 110;
const int mod = 2009;
struct Matrix
{
int a, b;
int c[N][N];
void init(int x = 0, int y = 0)
{
a = x, b = y;
memset(c, 0, sizeof (c));
}
void init_i(int x)
{
init(x, x);
a = b = x;
for (int i = 1; i <= x; ++i)
c[i][i] = 1;
}
friend Matrix operator*(const Matrix &a, const Matrix &b)
{
Matrix ret;
ret.init(a.a, b.b);
for (int i = 1; i <= a.a; ++i)
for (int k = 1; k <= b.b; ++k)
for (int j = 1; j <= b.a; ++j)
ret.c[i][k] = (1ll * a.c[i][j] * b.c[j][k] + ret.c[i][k]) % mod;
return ret;
}
} g;
Matrix ksm(Matrix a, int k)
{
Matrix ret;
ret.init_i(a.a);
for (; k; a = a * a, k >>= 1)
if (k & 1)
ret = ret * a;
return ret;
}
int main()
{
int n, t;
cin >> n >> t;
char c[20];
g.init(9 * (n - 1) + 9, 9 * (n - 1) + 9);
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= 8; ++j)
g.c[(i - 1) * 9 + j][(i - 1) * 9 + j + 1] = 1;
for (int i = 1; i <= n; ++i)
{
cin >> (c + 1);
for (int j = 1; j <= n; ++j)
{
if (c[j] > '0')
g.c[(i - 1) * 9 + c[j] - '0'][(j - 1) * 9 + 1] = 1;
}
}
g = ksm(g, t);
cout << g.c[1][(n - 1) * 9 + 1] << '\n';
return 0;
}
例2
在例1上面的基础上令 \(M[i][j] = \displaystyle\sum^k_{r = 1}in[i][r] \cdot out[j][r]\)。
其中 \(k\leq 20\),\(n\leq 1000\)。
我们在输入的时候把 \(out[k][j]\) 处理成 \(out[j][k]\).
于是就变成了 \(M[i][j] = in[i][j] \cdot out[j][r] = in\cdot out\)
显然直接 \(\mathcal O(n^3\log n)\) 的朴素矩阵乘法是不可以的。
于是 \(f_t = f_0\times M^t = f_0 \times in \times out \times in\times \dots \times out = f_0 \times in \times (in\cdot out)^{t - 1} \times out\)
\(in\cdot out\) 得到的就是 \(k\times k\) 的矩阵了,就可以 \(\mathcal O(k^3\log t)\) 了。
排列DP
排列定义:\(1\sim n\) 中的每一个数都只出现一次的序列。
\(1\sim n\) 有 \(n!\) 种排列。
一般问题:\(n!\)种排列中有多少个满足条件的排列。
第一维 \(f[i]\) 表示已经插入了 \(1\sim i\) 或 \(i\sim n\)。
例3
\(1\sim n\) 这 \(n\) 个数的排列有多少个排列有偶数个逆序对
变化的东西:逆序对数量、方案数。
\(f[i][j]\) 表示已经插入了 \(1\sim i\),有 \(j\) 个逆序对的方案数。
要把 \(i + 1\) 插到 \(k\)。由于是从小到大插入的,所以它前面的都比它小,后面的都比它大,所以会增加 \(i - k\) 个逆序对。
\(f[i][j]\to f[i + 1]f[i - k + j]\)
朴素:
点击查看代码
f[0][0] = 1;
for (int i = 0; i < n; ++i)
for (int j = 0; j <= i * (i - 1) / 2; ++j)
for (int k = 0; k <= i; ++k)
f[i + 1][j + i - k] += f[i][j];
可是我们只关注奇偶性,于是:
点击查看代码
#include <iostream>
int main()
{
f[0][0] = 1;
for (int i = 0; i < n; ++i)
for (int j = 0; j <= 1; ++j)
for (int k = 0; k <= i; ++k)
f[i + 1][(j + i - k) % 2] += f[i][j];
return 0;
}
优化到 \(\mathcal O(n^2)\) 了。
但是我们可以算出 \(1\sim i\) 有几个奇数、偶数,这样就优化到 \(\mathcal O(n)\) 了。
但这实际上是一个数学题,结论是 \(\dfrac{n!}{2}\)。
例4

\(f[i][j]\) 表示从 \(i\sim n\) 插入到 \(i\),有 \(j\) 个数满足条件的方案数。
这样,\(i - 1\) 无论插入到哪,满足条件的个数都不会减小。
但如果 \(i - 1\) 插入到了最前面,那它也会满足条件,所以个数会 \(+1\)。
所以
例5

不超过 \(2\),可以分为 \(1\) 和 \(2\),\(1\) 显然只有一种。
对于 \(2\),\(f[i][j]\) 表示选到第 \(i\) 个,所有的最长上升子序列的第二项最小坐标为 \(j\) 的方案数。
考虑插到 \(k\),如果 \(k = 0\),也就是插到最前面,最小坐标会往后移一位;否则,它会变成最小的坐标,所以
为什么是 \(k + 1\) 呢?因为插到第 \(i\) 个数后面,它的坐标是 \(i + 1\)。
区间 DP
对相邻的数进行运算。
例6
第一类区间 DP。
枚举断点。
点击查看代码
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int maxn = 110;
int a[maxn];
int sum[maxn << 1];
int dp[maxn << 1][maxn << 1];
int main()
{
memset(dp, 0x3f, sizeof (dp));
int n;
cin >> n;
for (int i = 1; i <= n; ++i)
{
cin >> a[i];
sum[i] = sum[i - 1] + a[i];
}
for (int i = n + 1; i <= n + n; ++i)
{
sum[i] = sum[i - 1] + a[i - n];
}
for (int i = 1; i <= n + n; ++i)
{
dp[i][i] = 0;
}
for (int len = 2; len <= n; ++len)
{
for (int l = 1, r = len; r <= n + n; ++l, ++r)
{
for (int k = l; k < r; ++k)
{
dp[l][r] = min(dp[l][r], dp[l][k] + dp[k + 1][r] + sum[r] - sum[l - 1]);
}
}
}
int ans = dp[1][n];
for (int i = 1; i <= n; ++i)
{
ans = min(ans, dp[i][i + n - 1]);
}
cout << ans << '\n';
memset(dp, 0, sizeof (dp));
for (int i = 1; i <= n + n; ++i)
{
dp[i][i] = 0;
}
for (int len = 2; len <= n; ++len)
{
for (int l = 1, r = len; r <= n + n; ++l, ++r)
{
for (int k = l; k < r; ++k)
{
dp[l][r] = max(dp[l][r], dp[l][k] + dp[k + 1][r] + sum[r] - sum[l - 1]);
}
}
}
ans = dp[1][n];
for (int i = 1; i <= n; ++i)
{
ans = max(ans, dp[i][i + n - 1]);
}
cout << ans << '\n';
return 0;
}
例7
同上。
点击查看代码
#include <iostream>
#include <vector>
#include <queue>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110;
int n;
int a[N << 1];
int l[N << 1], r[N << 1];
int f[N << 1][N << 1];
int calc(int i, int k, int j)
{
return l[i] * r[k] * r[j];
}
int main()
{
int n;
cin >> n;
for (int i = 1; i <= n; ++i)
cin >> a[i];
for (int i = 1; i < n; ++i)
l[i] = a[i], r[i] = a[i + 1];
l[n] = a[n];
r[n] = a[1];
for (int i = n + 1; i <= 2 * n; ++i)
l[i] = l[i - n], r[i] = r[i - n];
for (int len = 2; len <= n; ++len)
for (int i = 1, j = len; j <= 2 * n; ++j, ++i)
for (int k = i; k < j; ++k)
f[i][j] = max(f[i][j], f[i][k] + f[k + 1][j] + calc(i, k, j));
int ans = -1;
for (int i = 1; i <= n; ++i)
ans = max(ans, f[i][i + n - 1]);
cout << ans << '\n';
return 0;
}
例8

\(f[l][r]\) 表示删完了 \(l\sim r\)(\(l,r\) 不删)的最小总代价。
因此 \(f[l][r] = \displaystyle\min_{l < k < r}\{f[l][k] + f[k][r] + a_l\cdot a_r\cdot a_k\}\)。
答案即为 \(f[1][n]\)。
要保证状态和转移一致。
例9
求区间回文子序列个数。
是第二类区间 DP。
\(f[l][r]\) 表示 \(l\sim r\) 有多少个回文子序列。
转移:\(f[l][r] = f[l + 1][r] + f[l][r - 1] - f[l + 1][r - 1] + (s[l] == s[r])(f[l + 1][r - 1] + 1)\)。
例10

不能正常的枚举格子,算最小经过的被吓格子。
因为是老鼠数量,所以可能被一个老鼠吓好多次。
如果一个格子被老鼠吓到了第一次,那它最多走 \(2\) 步会再次被吓到。
所以再开两维记录上两步是怎么走的。
\(f[i][j][0/1][0/1]\) 表示走到了 \((i,j)\),上两步分别走的左/右、左/右,所经过的最少被吓格子。
例11
我们只需要魔改一下矩阵乘法,
把乘法改成类似于 Floyd 的更新答案。
每一次更新答案,就相当于多走了一条边。
因为 \(u,v\leq 10^3\),所以直接做是会炸的。
又注意到边数 \(\leq\) \(100\),所以点数 \(\leq\) \(99\)。
所以离散化一下就行了。
点击查看代码
#include <iostream>
#include <cstring>
using std::cin;
using std::cout;
const int N = 110;
const int K = 1010;
struct Matrix
{
int a, b;
int c[N][N];
void init(int x = 0, int y = 0)
{
a = x, b = y;
memset(c, 0x3f, sizeof(c));
}
void init_i(int x)
{
init(x, x);
a = b = x;
for (int i = 1; i <= x; ++i)
c[i][i] = 0;
}
friend Matrix operator*(const Matrix &a, const Matrix &b)
{
Matrix ret;
ret.init(a.a, b.b);
for (int i = 1; i <= a.a; ++i)
for (int j = 1; j <= b.b; ++j)
for (int k = 1; k <= a.b; ++k)
ret.c[i][j] = std::min(ret.c[i][j], a.c[i][k] + b.c[k][j]);
return ret;
}
} g;
int id[K];
Matrix ksm(Matrix a, int k)
{
Matrix ret;
ret.init_i(a.a); // 初始化为单位矩阵
for (; k; a = a * a, k >>= 1)
if (k & 1)
ret = ret * a;
return ret;
}
int main()
{
g.init();
int n = 0;
int l, t, s, e;
cin >> l >> t >> s >> e;
for (int i = 1; i <= t; ++i)
{
int w, u, v;
cin >> w >> u >> v;
u = id[u] ? id[u] : id[u] = ++n;
v = id[v] ? id[v] : id[v] = ++n;
g.c[u][v] = g.c[v][u] = std::min(g.c[u][v], w);
}
g.a = g.b = n; // 设置矩阵维度
Matrix ans = ksm(g, l);
s = id[s];
e = id[e];
cout << ans.c[s][e] << '\n';
return 0;
}
例12
这道题显然比较恶心。。。
转移矩阵:

而且这道题可能爆 long long,于是我们使用龟速乘。
虽然比较慢,但很好地解决了爆 long long 的问题。
点击查看代码
#include <iostream>
#include <vector>
#include <queue>
#include <cstdio>
#include <stack>
#include <cstdlib>
#include <cmath>
#include <ctime>
#include <set>
#include <map>
#include <cstring>
#include <algorithm>
#include <string>
#include <cstring>
#include <climits>
#include <assert.h>
#define dbg cout << "dbg"
using namespace std;
typedef long long ll;
const int N = 20;
struct Matrix
{
int a, b;
ll c[N][N];
void rs()
{
memset(c, 0, sizeof(c));
}
void rsi()
{
rs();
if (a != b)
while (1)
{
}
else
for (int i = 1; i <= a; ++i)
for (int j = 1; j <= b; ++j)
if (i == j)
c[i][j] = 1;
else
c[i][j] = 0;
}
};
ll n, m;
ll p, q, r, t, u, v, w, x, y, z;
ll tc(ll a, ll b)
{
ll ret = 0;
for (; b; a = (a + a) % m, b >>= 1)
if (b & 1)
ret = (ret + a) % m;
return ret % m;
}
Matrix operator*(const Matrix &a, const Matrix &b)
{
Matrix ret;
ret.rs();
ret.a = a.a;
ret.b = b.b;
for (int i = 1; i <= ret.a; ++i)
for (int j = 1; j <= a.b; ++j)
for (int k = 1; k <= ret.b; ++k)
{
ret.c[i][k] = (ret.c[i][k] + tc(a.c[i][j], b.c[j][k])) % m;
// cout << b.c[j][k] <<'\n';
// dbg;
// cout << i << ' ' << j << ' ' << k << '\n';
}
return ret;
}
void mo(Matrix &a)
{
for (int i = 1; i <= a.a; ++i)
for (int j = 1; j <= a.b; ++j)
a.c[i][j] %= m;
}
Matrix ksm(Matrix a, ll b)
{
Matrix ret;
ret.a = ret.b = a.a;
ret.rsi();
for (; b; a = a * a, b >>= 1)
{
// dbg;
if (b & 1)
ret = ret * a;
}
return ret;
}
int main()
{
cin >> n >> m;
cin >> p >> q >> r >> t >> u >> v >> w >> x >> y >> z;
Matrix l;
l.rs();
l.a = l.b = 11;
l.c[1][1] = p;
l.c[1][2] = 1;
l.c[1][3] = 1;
l.c[1][4] = q;
l.c[1][7] = r;
l.c[1][8] = t;
l.c[1][11] = 1;
l.c[2][1] = 1;
l.c[2][2] = u;
l.c[2][3] = 1;
l.c[2][5] = v;
l.c[2][9] = 1;
l.c[3][1] = 1;
l.c[3][2] = 1;
l.c[3][3] = x;
l.c[3][6] = y;
l.c[3][8] = 1;
l.c[3][10] = 1;
l.c[3][11] = 2;
l.c[4][1] = 1;
l.c[5][2] = 1;
l.c[6][3] = 1;
l.c[7][7] = 1;
l.c[7][8] = 2;
l.c[7][11] = 1;
l.c[8][8] = 1;
l.c[8][11] = 1;
l.c[9][9] = w;
l.c[10][10] = z;
l.c[11][11] = 1;
mo(l);
Matrix _;
_.rs();
_.a = 11;
_.b = 1;
_.c[1][1] = _.c[2][1] = _.c[3][1] = 3;
_.c[4][1] = _.c[5][1] = _.c[6][1] = 1;
_.c[7][1] = _.c[8][1] = _.c[11][1] = 1;
_.c[9][1] = w;
_.c[10][1] = z;
_.c[11][1] = 1;
mo(_);
// cout << n - 2;
Matrix res = ksm(l, n - 2) * _;
mo(res);
cout << "nodgd " << res.c[1][1] << '\n'
<< "Ciocio " << res.c[2][1] << '\n'
<< "Nicole " << res.c[3][1] << '\n';
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号