2025.5.1笔记
如果我有写错或令人不理解的地方,请及时指出,谢谢!!!
乐
不要用 endl —— 钟皓曦
颓
老师讲了许许多多可爱的数据结构和 STL,可是太简单了,只能颓一些小水题了。。。
Luogu SP3267 (莫队板子)
手写大根堆
点击查看代码
struct heap
{
int a[1010000];
int n = 0;
int top()
{
return a[1];
}
void push(int x)
{
n++;
int p = n;
a[n] = x;
while (p ^ 1)
{
if (a[p] > a[p >> 1])
{
swap(a[p], a[p >> 1]);
p >>= 1;
}
else
break;
}
}
void pop()
{
swap(a[1], a[n]);
n--;
int p = 1;
while ((p << 1) <= n)
{
int l = p << 1;
int r = l | 1;
int now = l;
if (r <= n && a[r] > a[l])
now = r;
if (a[now] > a[p])
{
swap(a[now], a[p]);
p = now;
}
else
break;
}
}
int size()
{
return n;
}
};
例1

给每个颜色开一个堆,再开一个新的堆,把所有颜色的堆顶放进来
题(洛谷)
点击查看代码
#include <queue>
#include <iostream>
#include <algorithm>
#define a first
#define b second
#define pii std::pair<int, int>
using std::cin;
using std::cout;
using std::priority_queue;
const int K = 60;
priority_queue<pii> p;
priority_queue<int> q[K];
int main()
{
int k;
cin >> k;
for (int i = 1; i <= k; ++i)
{
int n;
cin >> n;
for (int j = 1; j <= n; ++j)
{
int a;
cin >> a;
q[i].push(a);
}
}
for (int i = 1; i <= k; ++i)
{
if (q[i].size() > 0)
p.push({q[i].top(), i});
}
while (p.size() >= 3)
{
auto f = p.top();
p.pop();
auto s = p.top();
p.pop();
auto t = p.top();
p.pop();
if (s.first + t.first <= f.first)
{
int id = f.b;
q[id].pop();
if (q[id].size() > 0)
p.push({id, q[id].top()});
}
else
{
cout << f.b << ' ' << f.a << ' ' << s.b << ' ' << s.a << ' ' << t.b << ' ' << t.a << '\n';
return 0;
}
p.push(s);
p.push(t);
}
cout << "NIE" << '\n';
return 0;
}
例2
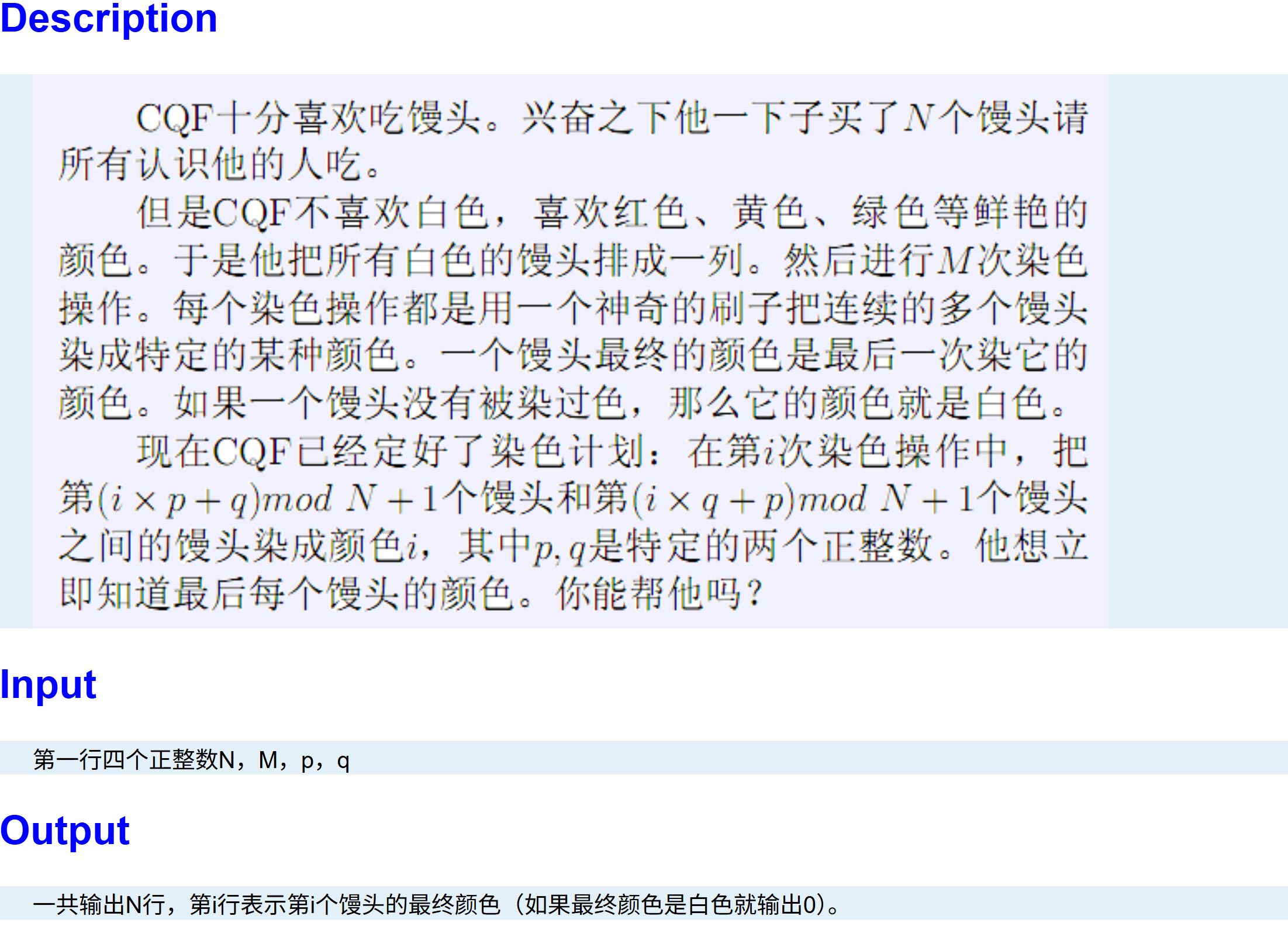

也就是给你一个长度 \(n\) 的空区间,有 \(m\) 个操作,每个操作 \(l, r, x\) 表示将区间 \(l\sim r\) 的位置改成 \(x\),最后输出每个位置的值。(\(n\leq 10^7\))
数据范围卡掉了线段树。(T_T)
于是并查集,达到几乎线性的复杂度。
点击查看代码
int main()
{
cin >> n;
for (int i=1;i<=n;i++)
to[i] = i;
for (int i=m;i>=1;i--)//倒着读 自己实现
{
int l,r,x;
//go(i) 从i向右 第一个没被染色的位置
cin >> l >> r >> x;//第i个操作
int p = go(l);
while (p<=r)//当前位置还在区间内
{
a[p] = x;//染色
int np = go(p+1);
to[p] = go(r+1);
p = np;
}
}
}
例3

先把每一个特殊点放进队列跑一遍bfs,求出其安全值。
把所有的点放到一个数组里,从大到小排序。
把这些点一个一个加到并查集里,直到 \((1, 1)\) 和 \((n, n)\) 在一个并查集里。
(我就不写了。。。)
例4
给你一个序列 \(a_1, a_2,\dots, a_n\) ,求 \(l, r\),满足 \(a_l \oplus a_{l + 1}\oplus\cdots \oplus a_r\) 最大.
先把它转换成前缀和 \(b_l, b_{l + 1},\dots, b_r\),则即求 \(b_{l - 1} \oplus b_r\) 最大。
便可用 01Trie。
写法:
点击查看代码
#include <iostream>
#include <algorithm>
#define int long long
using std::cin;
using std::cout;
// 增大节点数组的大小,防止节点数量不够
const int N = 32 * 1e5 + 10;
struct Node
{
int nxt[2];
Node()
{
nxt[0] = nxt[1] = 0;
}
} node[N];
int cnt;
int root = 1;
int a[N];
// 插入函数,将整数 x 插入到字典树中
void ins(int x)
{
int p = root;
for (int i = 30; i >= 0; --i)
{
int y = (x >> i) & 1;
if (!node[p].nxt[y])
{
cnt++;
node[p].nxt[y] = cnt;
}
p = node[p].nxt[y];
}
}
// 查询函数,查找与 x 异或结果最大的值
int query(int x)
{
int ans = 0;
int p = root;
for (int i = 30; i >= 0; --i)
{
int y = (x >> i) & 1;
// 优先选择与当前位不同的分支
if (node[p].nxt[y ^ 1])
{
p = node[p].nxt[y ^ 1];
// 将当前位设置为 1
ans ^= (1 << i);
}
else
{
p = node[p].nxt[y];
}
}
return ans;
}
signed main()
{
cnt = 1;
int n;
cin >> n;
for (int i = 1; i <= n; ++i)
cin >> a[i];
for (int i = 1; i <= n; ++i)
ins(a[i]);
int ans = 0;
for (int i = 1; i <= n; ++i)
ans = std::max(ans, query(a[i]));
cout << ans << '\n';
return 0;
}
例5
求 \(\displaystyle\sum^n_{l = 1}\sum^n_{r = l}(a_l\oplus\cdots a_r)\)。
算一下前缀和。
也就是求 \(\displaystyle\sum^n_{l = 1}\sum^n_{r = l}(b_{l - 1}\oplus b_r)\)。
异或对其他位无影响。
我们考虑:\(\displaystyle\sum^{n - 1}_{l = 1}\sum^n_{r = l + 1}(a_{l}\oplus a_r)\)。
考虑算每一位,如果这一对数对答案有贡献,那么它肯定是一个 \(0\),一个 \(1\)。
分步乘法计数原理,取 \(0\) 的方案数 \(\times\) 取 \(1\) 的方案数。
因此,这一位的贡献就是 所有数这一位上 \(1\) 的个数 \(\times\) 所有数这一位上 \(0\) 的个数 \(\times\) \(2^i\) 。
令 \(cnt_0 = 0\) 的个数,\(cnt_1 = 1\) 的个数。
如果是 \(\displaystyle\sum^{n - 1}_{l = 1}\sum^n_{r = l + 1}(a_{l} \& a_r)\)。
则每一位的贡献就是 \(\dfrac{cnt1 \cdot (cnt1 - 1)}{2} \cdot 2^i\)。
如果是 \(\displaystyle\sum^{n - 1}_{l = 1}\sum^n_{r = l + 1}(a_{l} | a_r)\)。
则每一位的贡献就是 \(\left[\dfrac{n\cdot (n - 1)}{2} - \dfrac{cnt0 \cdot (cnt0 - 1)}{2}\right] \cdot 2^i\)。
分块
只有两层,所以可以处理许多线段树处理不了的题。
点击查看代码
int belong[maxn]; // belong[i] 代表第i个数属于第几块
int sum[maxn]; // sum[i] 代表第i块的和是多少
int daxiao[maxn]; // daxiao[i] 代表第i块的大小是多少
int col[maxn]; // col[i] 代表第i块被整体加了col[i]
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> a[i];
int s = sqrt(n); // 每块的大小
for (int i = 1; i <= n; i++)
belong[i] = i / s + 1;
for (int i = 1; i <= n; i++)
{
sum[belong[i]] += a[i];
daxiao[belong[i]]++;
}
for (int x = 1; x <= m; x++)
{
int opt;
cin >> opt;
if (opt == 1) // 询问操作
{
int l, r;
cin >> l >> r;
int ans = 0;
if (belong[l] == belong[r])
for (int i = l; i <= r; i++)
ans += a[i] + col[belong[i]];
else
{
for (int i = l; belong[i] == belong[l]; i++)
ans += a[i] + col[belong[i]];
for (int i = r; belong[i] == belong[r]; i--)
ans += a[i] + col[belong[i]];
for (int i = belong[l] + 1; i < belong[r]; i++)
ans += sum[i];
}
cout << ans << "\n";
}
else
{
int l, r, v;
cin >> l >> r >> v;
if (belong[l] == belong[r])
for (int i = l; i <= r; i++)
a[i] += v;
else
{
for (int i = l; belong[i] == belong[l]; i++)
a[i] += v, sum[belong[i]] += v;
for (int i = r; belong[i] == belong[r]; i--)
a[i] += v, sum[belong[i]] += v;
for (int i = belong[l] + 1; i < belong[r]; i++)
{
sum[i] += v * daxiao[i];
col[i] += v;
}
}
}
}
return 0;
}
例6
每次询问 \(l, r\),求 \(a_l, a_{l + 1},\dots,a_r\) 中出现了偶数次的数有几个。
莫队。
不会莫队的请看 这里。
点击查看代码
#include <cmath>
#include <iostream>
#include <algorithm>
using std::cin;
using std::cout;
using std::sort;
const int N = 2e5 + 10;
int bel[N];
struct Query
{
int l, r, id;
friend bool operator<(const Query &a, const Query &b)
{
return bel[a.l] ^ bel[b.l] ? bel[a.l] < bel[b.l] : a.r < b.r;
}
} query[N];
int len;
int ans;
int a[N];
int cnt[N];
int ans_[N];
void ins(int x)
{
cnt[x]++;
if (cnt[x] % 2 == 0)
ans++;
else if (cnt[x] != 1 && cnt[x] % 2)
ans--;
}
void del(int x)
{
cnt[x]--;
if (cnt[x] != 0)
{
if (cnt[x] % 2 == 0)
ans++;
else
ans--;
}
}
int main()
{
int n;
cin >> n;
len = sqrt(n);
for (int i = 1; i <= n; ++i)
bel[i] = (i - 1) / len + 1;
for (int i = 1; i <= n; ++i)
cin >> a[i];
int q;
cin >> q;
for (int i = 1; i <= q; ++i)
{
int l, r;
cin >> l >> r;
query[i] = (Query){l, r, i};
}
int l = 1, r = 0;
sort(query + 1, query + q + 1);
for (int i = 1; i <= q; ++i)
{
int nowl = query[i].l;
int nowr = query[i].r;
int nowid = query[i].id;
while (r < nowr)
ins(a[++r]);
while (r > nowr)
del(a[r--]);
while (l < nowl)
del(a[l++]);
while (l > nowl)
ins(a[--l]);
ans_[nowid] = ans;
}
for (int i = 1; i <= q; ++i)
cout << ans_[i] << '\n';
return 0;
}
。。。代码应该是这样的。
这种排序可以证明是 \(O(n\sqrt{n})\) 的。
分治
求逆序对(归并排序)
点击查看代码
void merge(int l, int r) // 要计算l~r这个区间有多少个逆序对
{
if (l == r)
return;
int m = (l + r) >> 1; //(l+r)/2
merge(l, m); // 递归去算l~m的答案 a[l]~a[m] 排好序了
merge(m + 1, r); // 递归去算m+1~r的答案 a[m+1]~a[r] 排好序了
// i在左边 j在右边的答案
int p1 = l, p2 = m + 1;
for (int i = l; i <= r; i++)
{
if (p1 > m)
b[i] = a[p2], p2++;
else if (p2 > r)
b[i] = a[p1], p1++;
else if (a[p1] <= a[p2])
b[i] = a[p1], p1++;
else
b[i] = a[p2], p2++, ans += m - p1 + 1;
}
for (int i = l; i <= r; i++)
a[i] = b[i];
}
例7
看到涉及到整个 \(1\sim n\) 区间的所有子区间往分治上想。
考虑跨越中间的串有几个可以消。
首先,关于中间对称的可以消。
但 \(b|aab\) 也可以消掉。
于是,通过栈来求最简串(无法再消掉的串)。
(。。。没敲出来)
例8
板子,但 Luogu 卡了,只让莫队 133pts。
点击查看代码
#include <cmath>
#include <iostream>
#include <algorithm>
using std::cin;
using std::cout;
using std::sort;
const int N = 2e6 + 10;
int bel[N];
struct Query
{
int l, r, id;
friend bool operator<(const Query &a, const Query &b)
{
return bel[a.l] ^ bel[b.l] ? a.l < b.l : a.r < b.r;
}
}query[N];
int len;
int ans;
int x[N];
int cnt[N];
int ans_[N];
void ins(int x)
{
cnt[x]++;
if (cnt[x] == 2)
ans++;
}
void del(int x)
{
if (cnt[x] == 2)
ans--;
cnt[x]--;
}
void rd(int& x)
{
x = 0;
int f = 1;
char c = getchar();
while (c < '0' || c > '9')
{
if (c == '-')
f = -f;
c = getchar();
}
while (c >= '0' && c <= '9')
{
x = x * 10 + (c - '0');
c = getchar();
}
x = x * f;
}
void wt(int x)
{
if (x < 0)
{
putchar('-');
x = -x;
}
if (x <= 9)
{
putchar(x + '0');
return;
}
wt(x / 10);
putchar(x % 10 + '0');
}
int main()
{
int n, c, m;
rd(n), rd(c), rd(m);
// cout << n;
len = sqrt(n);
for (int i = 1; i <= n; ++i)
bel[i] = (i - 1) / len + 1;
for (int i = 1; i <= n; ++i)
rd(x[i]);
int l = 1, r = 0;
for (int i = 1; i <= m; ++i)
{
int l, r;
rd(l), rd(r);
query[i] = (Query){l, r, i};
}
sort(query + 1, query + m + 1);
for (int i = 1; i <= m; ++i)
{
int nowl = query[i].l;
int nowr = query[i].r;
int nowid = query[i].id;
while (r < nowr)
ins(x[++r]);
while (r > nowr)
del(x[r--]);
while (l < nowl)
del(x[l++]);
while (l > nowl)
ins(x[--l]);
ans_[nowid] = ans;
}
for (int i = 1; i <= m; ++i)
wt(ans_[i]), putchar('\n');
return 0;
}
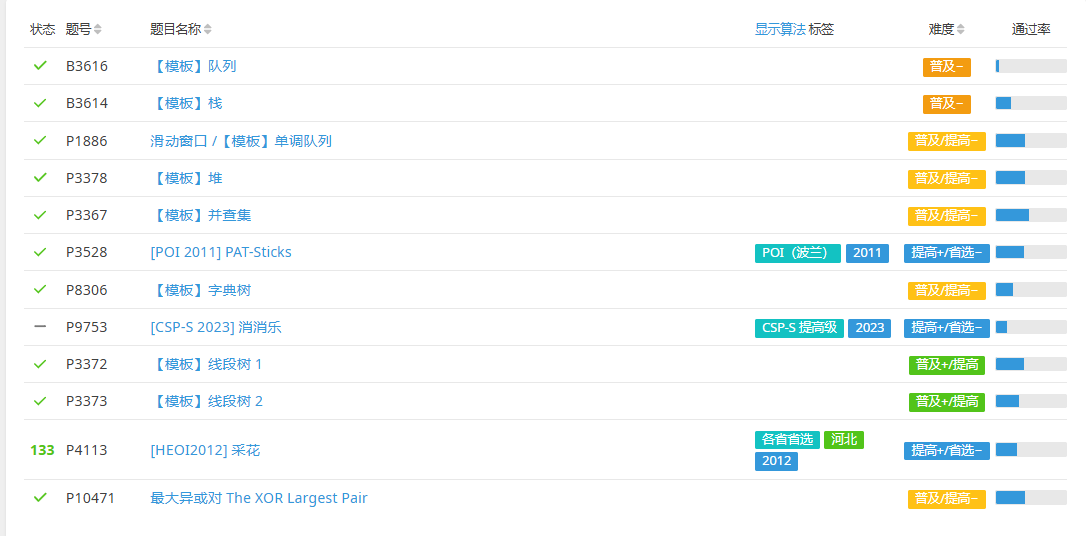
ryf大佬的题单
完成情况:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号