双十字相乘
二元二次式的分解!!!
引例
\(x^2 + 2xy - 3y^2 + 3x + y + 2\)
注意到,这个式子可以分出三个十字相乘出来.
即 \(x^2 + 2xy - 3y^2,x^2 + 3x + 2,-3y^2 + y + 2\) .
利用十字相乘的画法,分别得到:
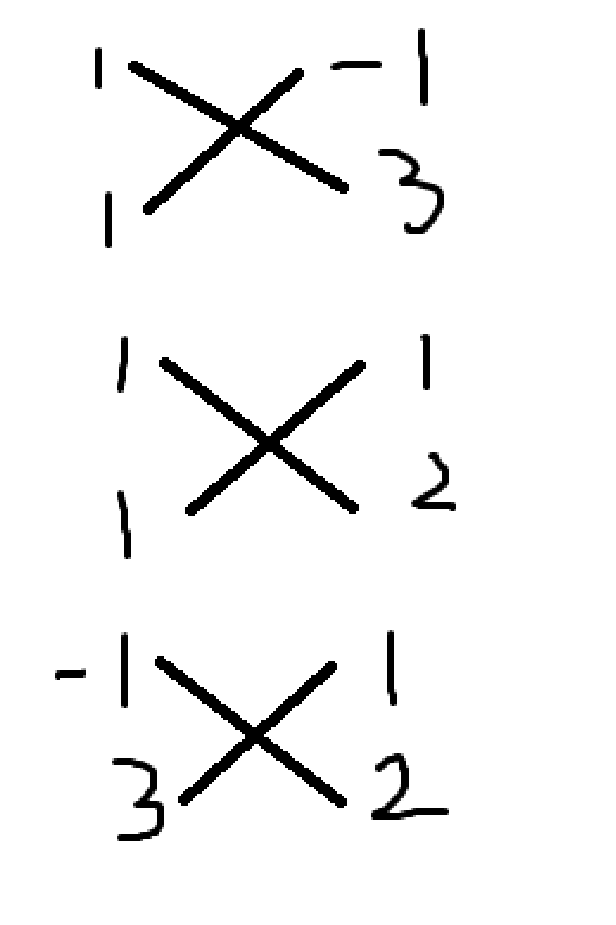
我们把它们调整,再组合一下,得到:
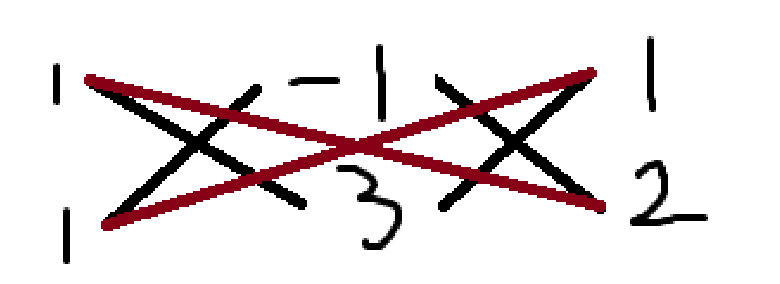
于是,原式 \(=(x - y + 1)(x + 3y + 2)\)
主要思想
-简单-来说,就是对于多项式 \(ax^2 + bxy + cy^2 + dx + ey + f\) ,将 \(a\) 表示为 \(a_1 \cdot a_2\) ,将 \(c\) 表示为 \(c_1 \cdot c_2\) ,将 \(f\) 表示为 \(f_1 \cdot f_2\) .使得 \(a_1c_2 + a_2c_1 = b, c_1f_2 + c_2f_1 = e, a_1f_2 + a_2f_1 = d\) .
即

则,原式 \(=(a_1x + c_1y + f_1)(a_2x + c_2y + f_2)\) .
题
\(x^2 + 2xy - 3y^2 + 3x + y + 2\)
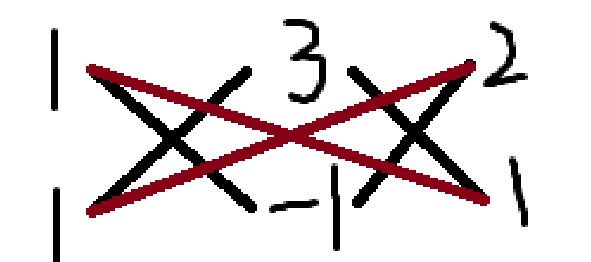
于是,原式 \(=(x + 3y + 2)(x - y + 1)\) .
\(6x^2 - 5xy - 6y^2 + 2x + 23y - 20\)
这道题系数有点大,不着急慢慢试.
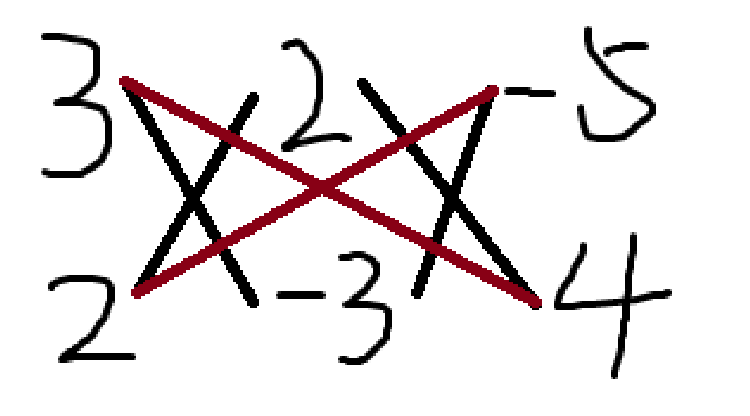
于是,原式 \(=(3x + 2y - 5)(2x - 3y + 4)\) .
\(x^2 - 6xy + 9y^2 - 5xz + 15yz + 6z^2\)
这道题虽然多了个 \(z\) ,但我们可以先忽略他,得到 \(x^2 - 6xy + 9y^2 - 5x + 15y + 6\) .将这个多项式进行分解,得到 \((x - 3y - 2)(x - 3y - 3)\) ,再将 \(z\) 带进去,得到 \((x - 3y - 2z)(x - 3y - 3z)\) .
这道题还有一个简便的做法:注意到 \(x^2 - 6xy + 9y^2\) 是完全平方式,于是,原式 \(=(x - 3y)^2 - 5(x - 3y)z + 6z^2=(x - 3y - 2z)(x - 3y - 3z)\) .
已知: \(a,b,c\) 为三角形的三条边,且 \(a^2 + 4ac + 3c^2 - 3ab - 7bc + 2b^2 = 0\) ,求证: \(2b = a + c\) .
证明:由题意得, \((a - 2b + c)(a + 3c - b) = 0\) .
又 \(\because a + c > b\) .
\(\therefore a + 3c > b\) .
\(\therefore a + 3c - b > 0\) .
\(\therefore a - 2b + c = 0\) .
\(\therefore 2b = a + c\) .
\(x^2 + 3xy + 2y^2 + 2x + 4y\)
这道题缺一个常数项,不妨我们给它补上,得
\(x^2 + 3xy + 2y^2 + 2x + 4y + 0\)
因为 \(0\) 乘上任何一个数都等于 \(0\) .所以常数项我们可以分解为 \(0\) 乘上任意一个数.
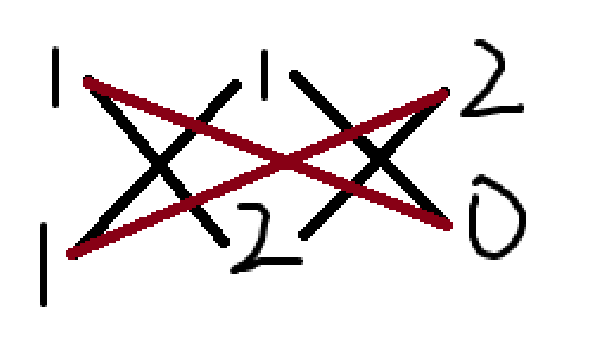
于是,原式 \(=(x + y + 2)(x + 2y)\)
当 \(m\) 为什么数得时, \(x^2 + 7xy - 18y^2 - 5x + my - 24\)
我们先考虑 \(x\) 与 \(y\) 和 \(x\) 与常数项的十字,可得
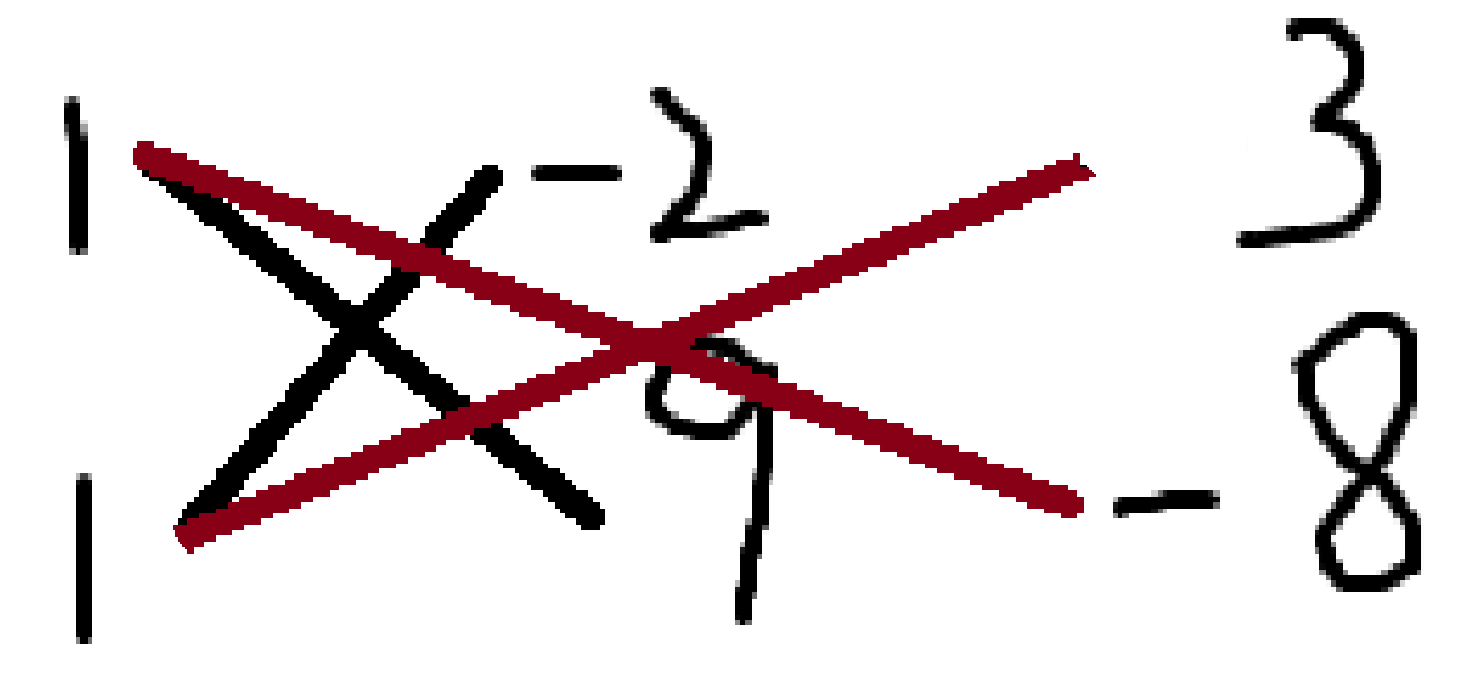
显然,因为 \(x\) 的系数是 \(1\times 1\) ,所以我们可以交换常数项(或 \(y\) )的两个数的位置,因此 \(y\) 和常数项的十字是
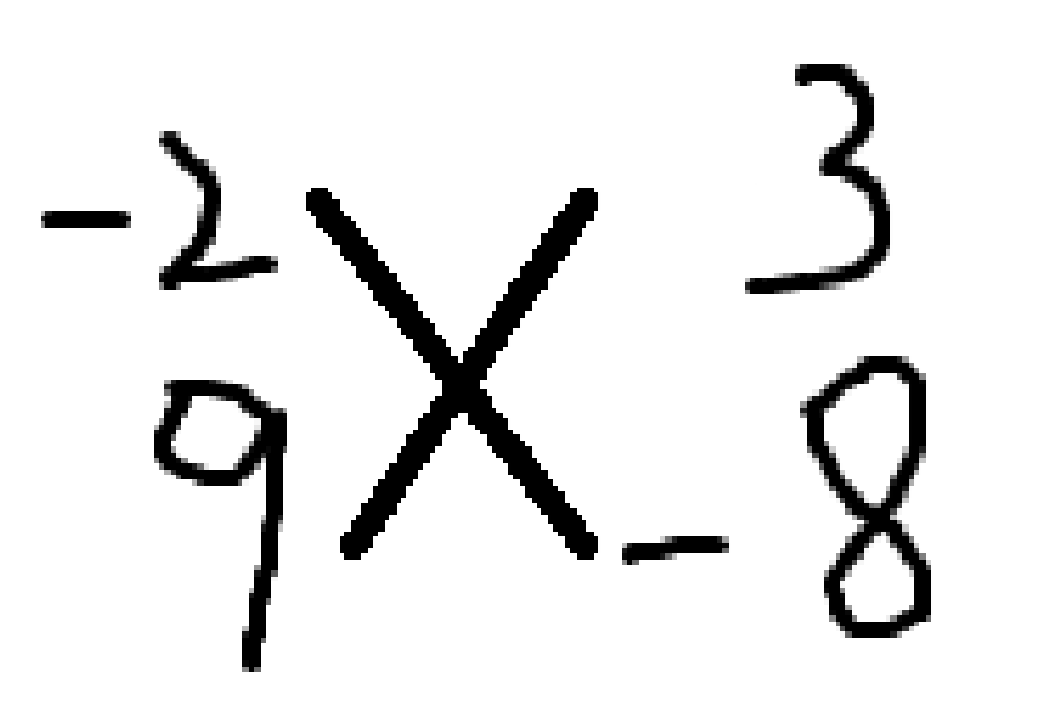
或
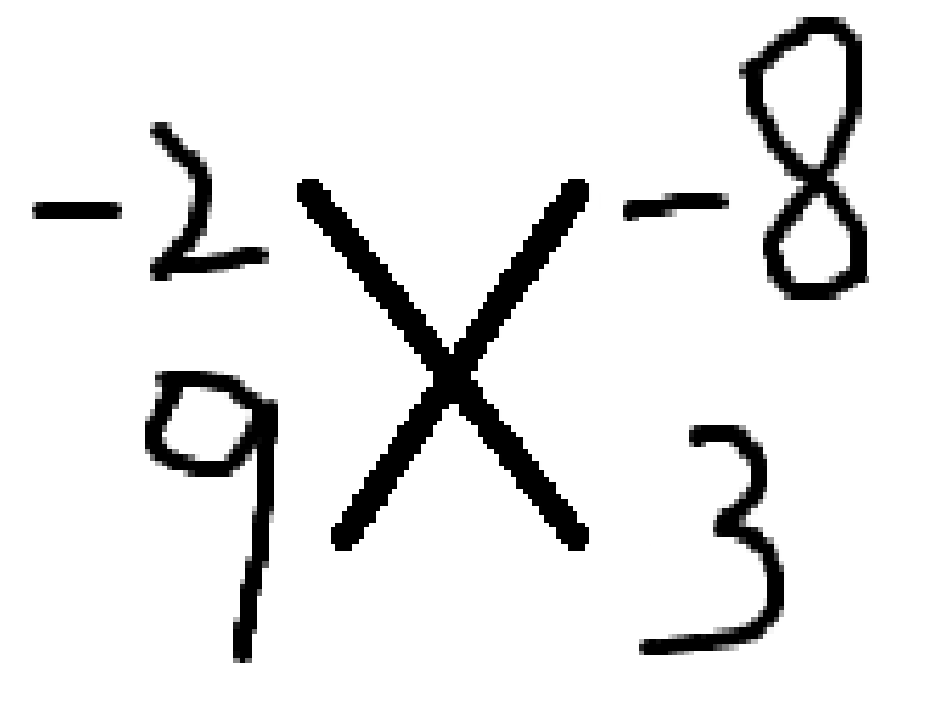
相乘再相加,得到的数是 \(43\) 和 \(-78\) .
于是, \(m = 43\) 或 \(m = -78\) .


 浙公网安备 33010602011771号
浙公网安备 33010602011771号