会员
周边
新闻
博问
闪存
众包
赞助商
Chat2DB
所有博客
当前博客
我的博客
我的园子
账号设置
会员中心
简洁模式
...
退出登录
注册
登录
PeterRabbi
博客园
首页
新随笔
联系
订阅
管理
2023年8月19日
ABAQUS子程序关联版本表与单位选择
摘要: 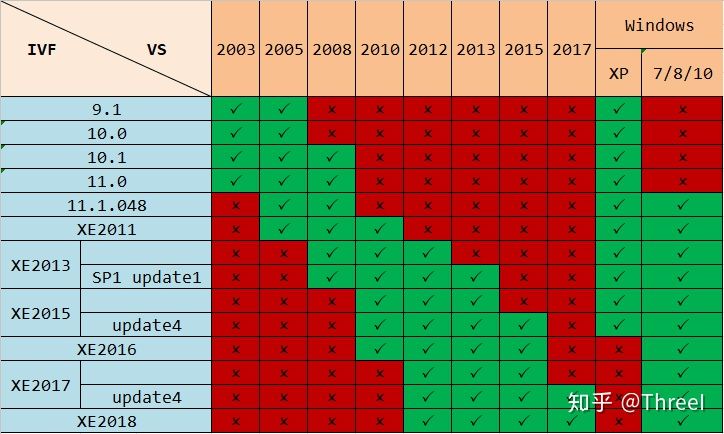 
评论(0)
推荐(0)
2023年6月14日
时域线性粘弹性(待完成)
摘要: ## Boltzmann叠加原理 对于==蠕变==,有 $\gamma(t)=J(t)\sigma$,其中 $J(t)=J_g+J_d\Psi(t)$。 假设在各个时间节点上施加一些列的 $\Delta\sigma(\tau_i)$ 外界激励,系统的一系列响应是 $J(t-\tau_i)$ ,相乘并
阅读全文
posted @ 2023-06-14 22:53 PeterRabbi
阅读(157)
评论(0)
推荐(0)
2023年6月6日
ABAQUS- UMAT-各向同性线弹性
摘要: ## 1. 各向同性线弹性本构模型 指标记法:$\sigma_{ij}=\lambda\varepsilon_{kk}\delta_{ij}+2\mu\varepsilon_{ij}$ $$ \begin{bmatrix} \sigma_1\\\sigma_2\\\sigma_3\\\sigma_4
阅读全文
posted @ 2023-06-06 16:57 PeterRabbi
阅读(747)
评论(0)
推荐(0)
卷积相关
摘要: 转自知乎 [如何通俗易懂地解释卷积?(作者:1335)](https://www.zhihu.com/question/22298352/answer/1071892762) 以及 [关于卷积本质的理解(作者:笨研)](https://zhuanlan.zhihu.com/p/34258488) 前
阅读全文
posted @ 2023-06-06 16:56 PeterRabbi
阅读(63)
评论(0)
推荐(0)
2023年5月15日
分数阶导数的基本概念与介绍
摘要: 重要参考 [ ] 华东师范大学 潘建瑜 教授 第一讲 分数阶微分方程 [ ] 维基百科分数微积分 [ ] 连接成功-知乎 慢慢推导柯西重复积分公式 [ ] 维基百科Gamma函数 以下是我的整理 一、学习的思路 我们熟知的是整数阶的微积分定义,分数阶微积分的定义一般就是由已知的定义推导而来的。所以学
阅读全文
posted @ 2023-05-15 20:35 PeterRabbi
阅读(1866)
评论(0)
推荐(0)
Laplace变换
摘要: 拉普拉斯变换 笔记摘录于悍将吴老二的视频关于拉氏变换这个视频就够了 一、引入概念 求解下面的方程会有困难,因为含有 $x(t)$ 的导数项。 $$ \dot{x}(t)+3x(t)=0 $$ 但是可以通过 $Laplace$ 变换来转化为下面的式子,求解 $x(s)$ 就会变得简单。 $$ sx(s
阅读全文
posted @ 2023-05-15 19:10 PeterRabbi
阅读(290)
评论(0)
推荐(0)
公告