斜率优化相关小记

这里的“斜率优化”不是狭义上的。

wqs 二分

（借用了 https://www.cnblogs.com/ydtz/p/16536706.html#gallery-3 这个博客的图）

黑科技简介

wqs 二分是王钦石于 2012 年国家集训队论文中提出的一种处理限制类问题的方法，如“选 \(K\) 个”。

对于类似这样的问题，若可以证明答案是一个凸函数，则一般可用 wqs 二分求解。而有时证明答案是个凸函数不容易，需要用到严谨的数学证明，所以一般是通过猜测和观察样例的方式求证。

算法思想

假设现在有一个最优化问题，强制选择 \(k\) 个物品，求最大收益（满足答案是凸函数）。

我们以上凸函数为例，设选择 \(x\) 个物品的最优答案为 \(f(x)\)。我们考虑如何求出这个 \(f(x)\)。

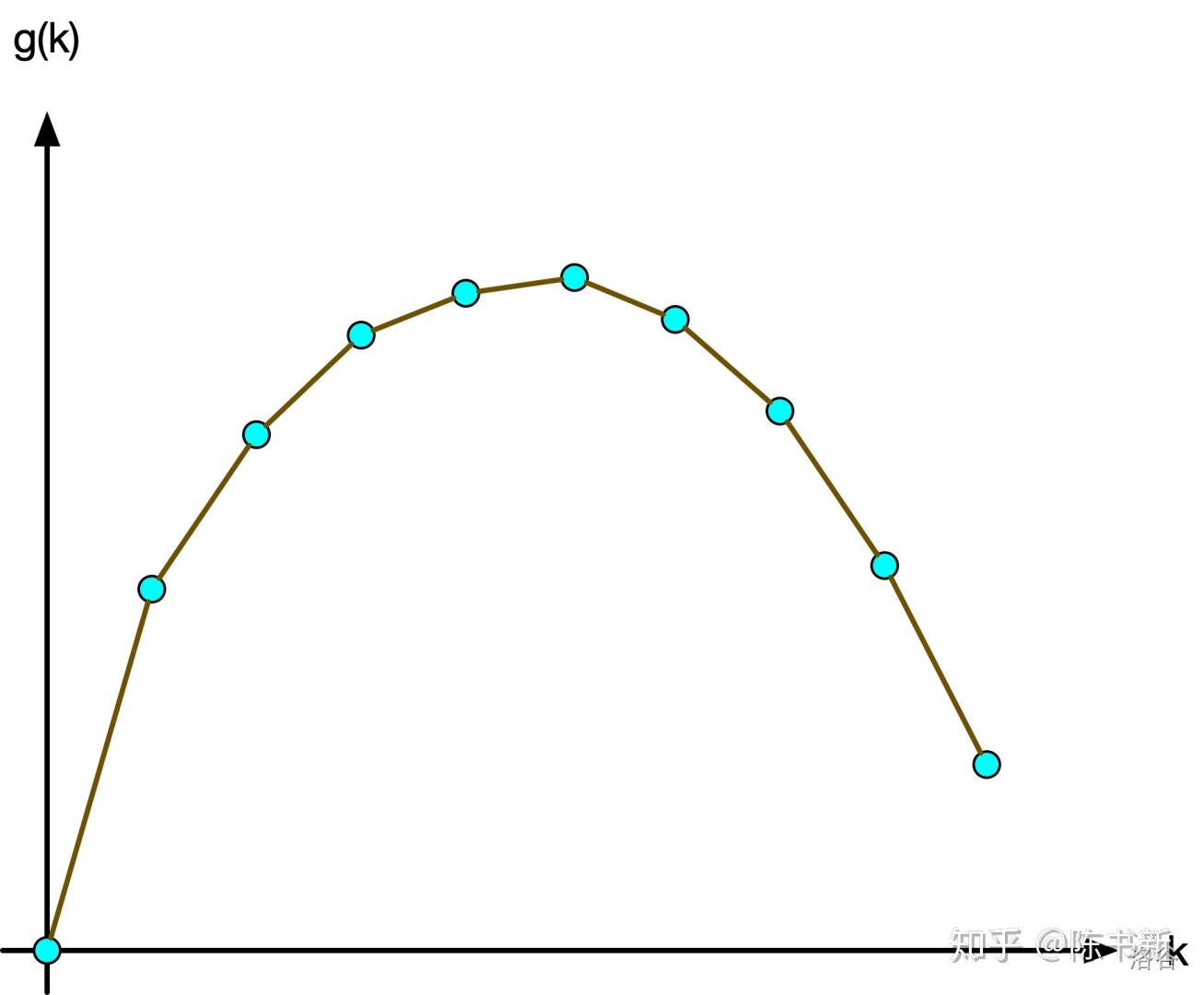
由于 \(f(x)\) 是上凸函数，因此满足 \(f(x)\) 的导函数单调不升，即 \(f(x)\) 的斜率单调不升。那么斜率满足单调性，我们可以二分斜率，这也是 wqs 二分中“二分”的由来。

我们考虑对于一个二分的斜率 \(k\) 怎么写 check 函数。

我们二分的 \(k\) 对应的方程是一次函数 \(g=kx+b\)，且我们令它是 \(f\) 的切线方程，若当前 \(g\) 与 \(f\) 的切点对应的 \(x\) 坐标与题目要求的偏小，则说明应当把斜率变小，反之应当把斜率变大。

但是我们如何求出这个 \(x\) 呢？\(g\) 是斜率为 \(k\) 的截线，而截距 \(b\) 是未知的，因此与 \(f\) 会有无数个交点，即 \(f(x_{1})=g(x_{1}), \dots, f(x_{n})=g(x_{n})\)。

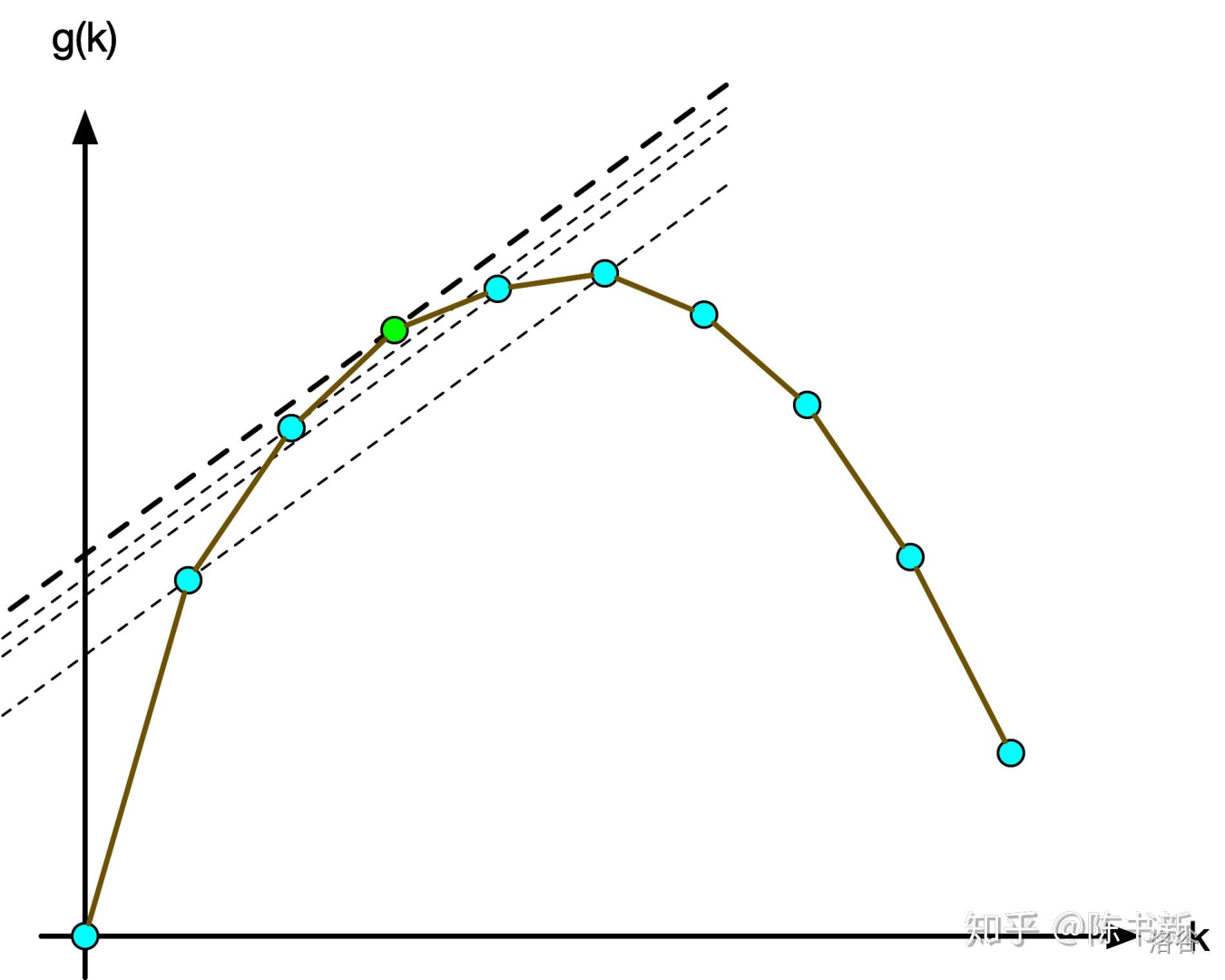
但是我们注意到，真正和 \(f\) 相切的那条截线 \(g(x)\)，满足它的截距 \(b\) 是最大的，即 \(f(x)=g(x)=kx+b_{x},b_{x}=b_{\max}\)。

我们引入“惩罚系数”这一概念，对上式进行移项：\(b_{x}=f(x)-kx\)，那么不仅仅对于切线，对于 \(\forall i\) 均有 \(b_{i}=f(i)-ki\)，因此这个 \(b\) 的含义大概解释就是，如果我选了 \(i\) 个数，那么每个数的代价均减去 \(k\) 后的最优答案。

可以发现这样处理后我要求的 \(x\) 这个点，由于是切点，\(b\) 值是最大的，因此此时我可以忽略“选择 \(K\) 个”这一限制，我直接求全局最优解，对应的就是此时二分的斜率对应切点的横坐标值。

所以在 check 里，先把每个权值/代价减去 \(k\)，只需在求解全局最优时顺便记录选择的个数即可。check 里可以是 dp，也可以是贪心，要看具体题目。

假如我们找到了对应横坐标，那么此时的答案也就是题目问的答案，但注意，由于你引入了“惩罚系数”，因此需要把答案加上 \(K \times mid\)，其中 \(mid\) 是二分的斜率，也就是“惩罚系数”。

这样的话，我们省去了“选择 \(K\) 个数”这一限制，复杂度由一般的 \(O(nK)\) 变成了 \(O(n \log V)\)，其中 \(V\) 一般是值域，是一种非常高效的算法。

一些细节

对于一个凸函数，可能存在几个点斜率相同的情况：

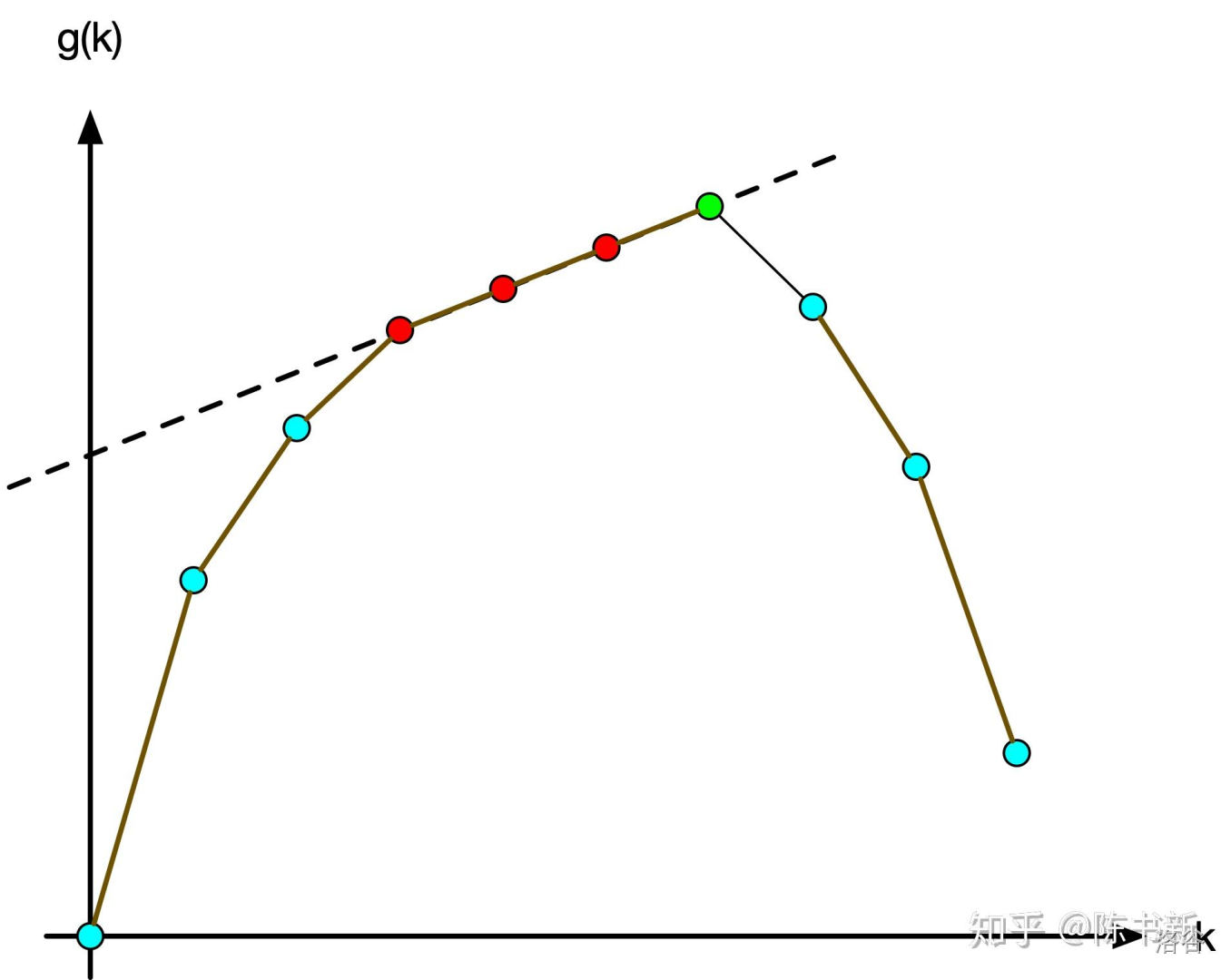
假如问题横坐标就是一个红点，但你此时 check 出的横坐标可能是三个红点或绿点中的任意一个，这个如何解决？

其实很简单，例如对于这个上凸函数，我们在跑全局最优解的前提下，我们使得选中的数尽量大，那么 check 出的横坐标天然落在绿点上。对于判定 check 函数是否合法，我们这么写：

int cnt=check(mid);
if(cnt>=K) ans=res+K*mid;

不写 \(cnt \times mid\) 而是 \(K \times mid\) 的原因就是可能存在若干点共线的情况。

简单扩展

其实“至少选 \(K\) 个”或者“至多选 \(K\) 个”问题也是可以使用 wqs 二分的。

但这种情况就变成了一个区间的最优答案。这里以“至少选 \(K\) 个”，上凸函数为例。

我们先检查这个凸函数的凸顶，即斜率为 \(0\) 的点对应的横坐标是否 \(\le K\)，如果是，那么直接输出即可；如果不是，则说明这个上凸函数在 \([1,K]\) 是单调上升的，那么问题变成了“强制选 \(K\) 个”。

例题

洛谷 P1484 种树

这个是 wqs 二分的模板题，容易写出 \(O(nk)\) 的 dp，然后容易发现答案是凸的，因为开始选多个肯定不劣，到后面正数都选完了，被迫选负数，这时肯定不优。然后打个表看一下是上凸还是下凸，调整一下二分策略就做完了，记得要先判断函数能不能取到凸顶。

时间复杂度 \(O(n \log V)\)。

洛谷 P2619 [国家集训队] Tree I

二分斜率后，把所有的白边权值减去 \(mid\)，然后在 check 里跑 kruscal 生成树，在权值相同的情况下我们优先选择白边，是为了处理可能的多点共线的情况。

AtCoder Beginner Contest 400G - Patisserie ABC 3

先考虑朴素的 dp 怎么实现。发现题目的贡献计算形式比较难搞，考虑把它拆开。

具体地，我们设 \(f_{i,j,a,b,c}\) 表示前 \(i\) 个数已经选择了 \(j\) 个，贡献计算方式为 \(X,Y,Z\) 的选择个数的奇偶性为 \(a,b,c\) 的最大价值。容易发现这样设计 dp，我们只需单独考虑一个数选择哪一维作为贡献，因为最终的最大值一定存在于某种决策中，这个需要感性理解一下。

那么最终的答案为 \(f_{n,k,0,0,0}\)。

这样做的复杂度为 \(O(nk)\)，容易证明这个答案也是关于 \(k\) 的一个凸函数，考虑 wqs 二分优化，那么可以去掉限制，跑全局的最优答案即可。

时间复杂度为 \(O(2^c n \log V)\)，本题中 \(c=3\)。

斜率优化动态规划

（借用了 https://www.cnblogs.com/Plozia/p/16155799.html 的图）

算法简介

斜率优化 dp 是一种常见的优化 dp 转移的方式，其依赖于状态转移方程的形式。

算法思想

假设一个动态规划的转移方程形如 \(f_{i}=\min\limits_j\{f_{j}+a_{i}a_{j}\}\)，直接暴力求解的复杂度是 \(O(n^2)\) 的。

我们观察这个式子，先把 \(\min\) 符号忽略，即 \(f_{i}=a_{i}a_{j}+f_{j}\)，这个与一次函数 \(y=kx+b\) 形式很接近，但是我们令 \(f_{i}=b,a_{i}=-k,a_{j}=x,f_{j}=y\)。

这样做的原因可以参考上文的 wqs 二分，因为斜率的性质是切点处截距 \(b\) 有极大值/极小值，这会方便后面的讨论。

那么式子变成了 \(b=-kx+y\)，且 \((x,y)=(a_{j},f_{j})\)，因此所有转移点可以视为平面坐标系上的若干个点。

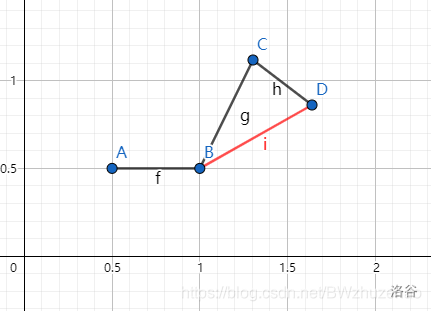
假如此时我有 \(A,B,C,D\) 四个转移点。由上述内容，我要使 \(b\) 最小化，相当于用斜率为 \(k(-a_{i})\) 的直线去截这些点，求截距最小的那个。

然后你会发现这个 \(C\) 点其实是没用的，因为无论是什么斜率去截 \(C\) 点都不是最优的，所以可以把类似 \(C\) 的点去掉。

然后这个其实是一个下凸壳，我们只需要维护这个下凸壳就行，就是一个斜率单调不降的凸包，这个容易用一个单调队列去维护。

假设我们有了这个下凸壳，求答案就变成了求相切点，因为这个点是凸壳所有点截距最小的，这一点和 wqs 二分一致。

我们设凸壳中点 \(i\) 的斜率为 \(\dfrac{y_{i+1}-y_{i}}{x_{i+1}-x_{i}}\)，凸壳的最后一个点斜率为 \(+\infty\)。

求这个切点我们依旧可以二分凸壳中的斜率，找到第一个斜率大于等于 \(k\) 的点，这个点就是斜率为 \(k\) 的直线与凸包相切的点，这个点的信息也就是当前转移的最优点。

当然了，有时候我们不需要这个二分。具体而言，有时候 \(1 \sim n\) 所需要查询的斜率是单调不减的，那么我们将单调队列改为双端队列，把队头小于 \(k\) 的斜率踢出，每次我所需要的点就是队头。

slope trick

参考资料：https://www.cnblogs.com/Garbage-fish/p/18710010

请注意，slope trick 和狭义的斜率优化不是同一个东西，狭义的斜率优化是 Convex Hull Trick。

这玩意比 wqs 抽象多了（

黑科技简介

对于 slope trick，我们认为一个函数是可斜率优化的，它需要满足以下性质：

1. 函数是凸函数，即斜率单调不增或单调不降。

2. 函数由若干个一次函数构成。

3. 函数是连续的。

然后 slope trick 它的凸包和上文 wqs 二分和普通斜率优化的凸包不太一样，这里下文会有所提及。

算法思想

温馨提示：下文中若无特殊说明，“凸函数”均指“下凸函数”。

我们称一个点是拐点，当且仅当这个点属于两个斜率不同的直线，且这个点是这两条直线的交点。

首先，slope trick 的核心思想是用拐点维护凸包，因为是若干个一次函数，那么拐点确定了，这个凸包也就确定了。

然后我们考虑一个函数 \(f(x)=|x|\)，这个函数是可斜率优化的。

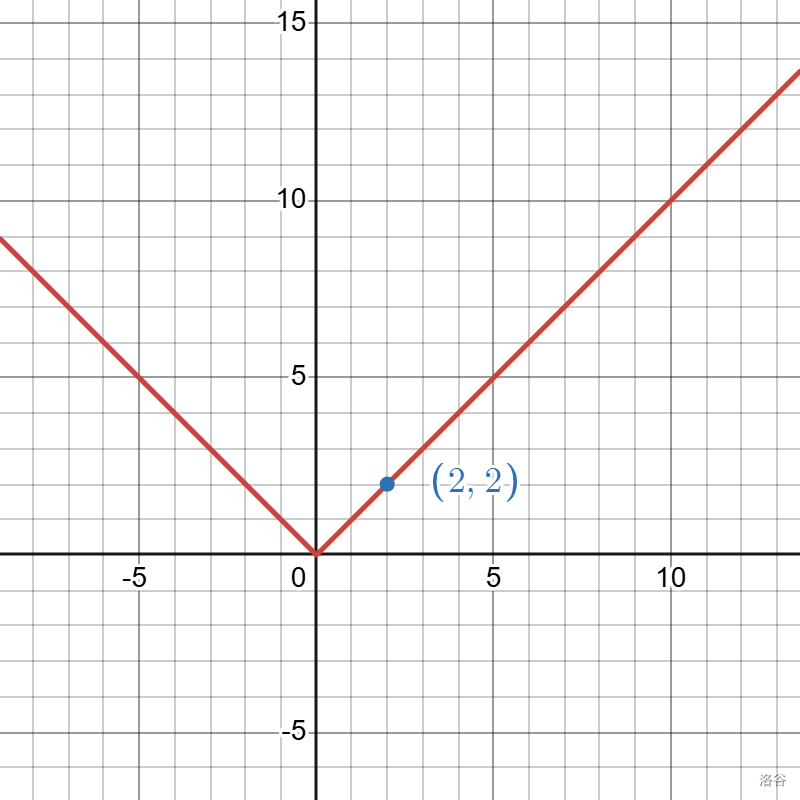
在这个凸包中，唯一的拐点坐标是 \((0,0)\)，但只知道这个信息是无法知道整个凸包的状态的，因此对于一个拐点 \(A\)，设经过这个拐点后斜率变化为 \(k\)，则我们在可重集里丢进 \(|k|\) 个拐点的横坐标的值。

可以发现，在这样的构造方式下，我们只需要知道任意一段直线的解析式，整个凸包是唯一的。

这里需要说明的是，我们认为一个拐点的斜率是拐后直线的斜率，否则这个是未定义的。

通过维护这个可重集 \(S\)，有一些性质和基本操作。

1.凸包具有可加性

可斜率优化的函数是可以合并的，这里的“可合并”包括斜率、截距、可重集 \(S\) 等。

这里强调一下，\(S\) 里面维护的是拐点的横坐标！

例如，对于两个凸函数 \(f(x)\) 和 \(g(x)\)，我们定义 \(h(x)=f(x)+g(x)\)，则 \(h(x)\) 也是凸函数，且满足：

\[\begin{cases}k_h=k_f+k_g\\b_h=b_f+b_g\\S_h=S_f \cup S_g\end{cases} \]

可重集的合并是取并集，例如 \(S_f=\{1,1,2,3\},S_g=\{2,3,4\}\)，则 \(S_h=\{1,1,2,2,3,3,4\}\)。

那么怎么简单地去维护这个 \(S\) 呢？对于一般地问题而言，我们都是把 \(S\) 拆成两段（或者说三段）来维护，第一段是斜率为负的函数段，第二段是斜率为 \(0\)，第三段是斜率为正的函数段。

我们用大根堆维护第一段，用小根堆维护第三段。

下面我们假设这个凸函数包含以上三段。

这样的话，假设凸函数斜率最小为 \(k\)，则大根堆的元素个数应该等于 \(|k|\)，因为我们构造可重集的方式就是斜率变化的大小，而第一段斜率为 \(k\)，它要变化到 \(0\)，有 \(|k|\) 个元素。

小根堆也是同理了。

假设当前我有一个集合 \(A\) 要并到 \(S\) 里去，如果并完后此时大根堆的元素有 \(c\) 个，超过了 \(|k|\)，那么显然有多的元素应当丢到小根堆里去，应该丢的是堆顶的 \(c-|k|\) 个元素，因为显然横坐标越大它对应的斜率也越大。