DP专题-学习笔记:斜率优化 DP
一些 update
update 2021/4/19:最近在洛谷讨论区的学术版里面看到一篇帖子,是关于斜率相同时是否需要弹出队列的问题,笔者在看完这篇帖子之后,发现这个细节是很重要的,故加上。
update 2022/1/8:修改了一个地方的语言,不影响本篇文章的理解,但是对于一些斜率优化的题目还是有影响的。
1. 前言
斜率优化 DP,是一种优化动态规划的方式,采用线性规划的方式来优化动态规划。
斜率优化 DP 一般是拿来优化 1D/1D 的动态规划的。
什么是 1D/1D 的动态规划?
1D/1D 的动态规划就是指状态是一维,转移也是一维的动态规划。
式子一般长这样:\(f_i=\min/\max\{A|j<i\}\),其中 \(A\) 是关于 \(j\) 的一个有特殊条件的式子。
代码一般长这样:
for (int i = 1; i <= n; ++i)
for (int j = 0; j < i; ++j)
f[i] = Min/Max(f[i], 某个跟 j 有关的特殊式子);
那么这个特殊条件是什么呢?
这种 DP 的转移方程分 2 类:
- 形如 \(f_i=A+B\) 的,其中 \(A\) 是一个只关于 \(i\) 的式子,\(B\) 是一个只关于 \(j\) 的式子。
像这样的 DP,一般是可以采用单调队列/单调栈/数据结构维护的。 - 形如 \(f_i=A+B+C\) 的,其中 \(A,B\) 同上,\(C\) 是一个存在形如 \(a_i \times b_j\) 的项的式子,比如说 \(f_i=f_j+(i-j)^2\)。
这个时候,如果你将这个式子拆开就会发现,里面存在一个项 \(2ij\),此时普通的单调队列就不能解决了,需要采用斜率优化。
斜率优化是基于单调队列实现的,因此请先学习单调队列。
注意本文所讨论的所有题目默认求的斜率单调递增,如果不是单调递增请采用李超线段树解决。
李超线段树实际上是更加一般的做法,复杂度是 \(O(n \log v)\)(\(v\) 是值域注意不直接是 \(a_i\) 值域),详情请见:数据结构专题-学习笔记:李超线段树
2. 详解
2.1 暴力方程
斜率优化的第一步是设计出暴力方程而且要是 1D/1D 的。
设 \(f_i\) 表示从 1 到 \(i\) 分段之后的最大战斗力,\(s_i\) 为 \(x_i\) 的前缀和数组,那么就有状态转移方程:$$f_i=\max{f_j+a(s_i-s_j)^2+b(s_i-s_j)+c|0 \leq j<i}$$
初值为 \(f_0=0\),其余为 \(-inf\)。
这个方程应该还是很好理解的吧~
暴力得分 50pts。
我第一次写暴力的时候出了点意外得 40pts
2.2 线性规划
接下来考虑优化。
斜率优化,肯定跟斜率有关。
而斜率优化的关键步骤如下:
- 拆式子。
- 化成形如 \(y=kx+b\) 的式子。
- 根据求 \(f_i\) 的 \(\max\) 还是 \(\min\) 决定维护上凸壳还是下凸壳。
什么意思呢?
考虑拆式子,拆成 \(y=kx+b\),其中 \(y,x\) 与 \(j\) 有关,\(k,b\) 与 \(i\) 有关,所有常数项放到 \(b\) 中。
先将原始方程拆掉:\(f_i=f_j+as_i^2+as_j^2-2as_is_j+bs_i-bs_j+c\)
拆掉了之后,根据上述描述,转变式子:\(f_j+as_j^2-bs_j=2as_is_j+f_i-as_i^2-bs_i-c\)
此时此刻 \(y=f_j+as_j^2-bs_j,k=2as_i,x=s_j,b=f_i-as_i^2-bs_i-c\)。
那么考虑 \(y=kx+b\) 的几何意义,那么就可以看成过点 \((s_j,f_j+as_j^2-bs_j)\) 的直线,其中斜率 \((k,b)=(2as_i,f_i-as_i^2-bs_i-c)\),我们的任务是让截距 \(b\) 最大化。
考虑下面这张图:
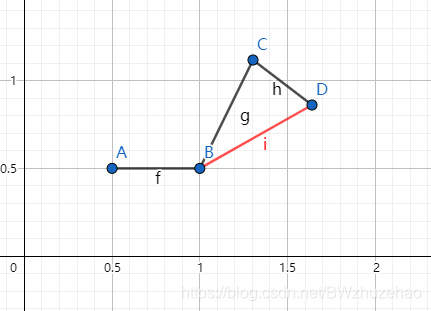
显然,对于相同的斜率 \(k\),过 D 点的截距肯定比过 C 点的截距要小。
这个可以利用线性规划理解。
因此基本思路就出来了:要使截距最大化,肯定要使斜率逐渐变小(结合上图理解);要使截距最小化,肯定要使斜率逐渐变大。
而对于前面的几个点,如果其斜率大于了 \(k\),那么显然当前点比直接从 \(i\) 点分割更劣,直接删掉即可。
对于后面的几个点,采用类似单调队列的方式保证斜率单调即可。
从图像上,使截距最大化就是使斜率递减,也就是维护上凸壳;使截距最小化就是使斜率递增,也就是维护下凸壳。
那么如何记转换式子呢?\(y=kx+b\),\((x,y)\) 与 \(j\) 有关,\((k,b)\) 与 \(i\) 有关,这样记就好了。
因此,对于上面的方程,采用单调队列维护一下斜率,然后每一次取出队尾(因为此时队尾一定是最优的),这样就可以做到 \(O(n)\) 解决。
关于队首与队尾的斜率相同时是否需要弹出队列的问题:
假设当前的点是这样的:
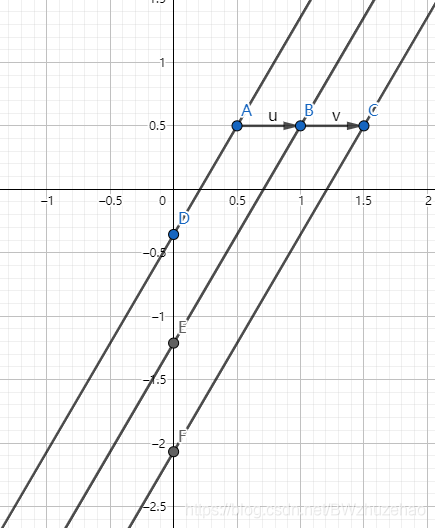
从图上可以清晰的看出来,对于 A,B,C 这三个点,其斜率全部都是相同的,而且前缀和也没有变化,貌似是可以弹出,但是看一下这条直线在这三个点上的截距 OD,OE,OF,会发现截距大小是不同的,而截距不同也会代表着 \(f_i\) 不同,如果选择弹出,程序可能会选择 AD 这条线,但是正确的答案是 CF 这条线。
2.3 代码
这里给一个保证写斜率优化代码正确的小技巧:
首先写暴力方程,然后写暴力程序,确定没问题就可以直接推式子斜率优化,最后两者对拍。
当然如果暴力方程写对了一般斜率优化是不会出问题的。
代码如下:
/*
========= Plozia =========
Author:Plozia
Problem:P3628 [APIO2010]特别行动队
Date:2021/4/15
========= Plozia =========
*/
#include <bits/stdc++.h>
typedef long long LL;
const int MAXN = 1e6 + 10;
int n, l, r, q[MAXN];
LL a, b, c, x[MAXN], f[MAXN];
LL read()
{
int sum = 0, fh = 1; char ch = getchar();
for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = (sum << 3) + (sum << 1) + (ch ^ 48);
return sum * fh;
}
LL Min(LL fir, LL sec) { return (fir < sec) ? fir : sec; }
LL Max(LL fir, LL sec) { return (fir > sec) ? fir : sec; }
double K(int i) { return 2.0 * a * x[i]; }
double X(int i) { return 1.0 * x[i]; }
double Y(int i) { return 1.0 * f[i] + a * x[i] * x[i] - b * x[i]; }
double Slope(int x, int y) { return (Y(x) - Y(y)) / (X(x) - X(y)); }
int main()
{
n = read(), a = read(), b = read(), c = read();
memset(f, -0x3f, sizeof(f)); f[0] = 0;
for (int i = 1; i <= n; ++i) x[i] = read() + x[i - 1];
q[l = r = 1] = 0;
for (int i = 1; i <= n; ++i)
{
while (l < r && Slope(q[l], q[l + 1]) >= K(i)) ++l;//队头删除
int j = q[l]; f[i] = f[j] + a * (x[i] - x[j]) * (x[i] - x[j]) + b * (x[i] - x[j]) + c;//转移
while (l < r && Slope(q[r], q[r - 1]) <= Slope(q[r], i)) --r;//队尾删除
q[++r] = i;
}
// for (int i = 1; i <= n; ++i)
// for (int j = 0; j < i; ++j)
// f[i] = Max(f[i], f[j] + a * (x[i] - x[j]) * (x[i] - x[j]) + b * (x[i] - x[j]) + c);
printf("%lld\n", f[n]); return 0;
}
3. 总结
-
使截距最大化维护上凸壳,使截距最小化维护下凸壳。
-
将方程转变为 \(y=kx+b\),\((x,y)\) 与 \(j\) 有关,\((k,b)\) 与 \(i\) 有关。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号