DP 凸优化(WQS 二分 & Slope Trick) 笔记
本文原在 2025-01-21 08:36 发布于本人洛谷博客。
一、WQS 二分
考虑有下面这个问题:
有 \(n\) 个物品,每个物品有价值 \(a_i\),价值有正有负,你选择恰好其中 \(m\) 个物品求最大价值。
其实直接贪心就能做,但是考虑下面这种做法:
假如五个物品的价值分别是 \(\{5, 3, 2, -3, -4\}\),\(m=2\),设 \(f(i)\) 表示恰好选 \(i\) 个物品的最大值,那 \(f\) 的函数图像可以如下图所示。

称这种斜率(即一次函数 \(y=kx+b\) 的 \(k\))单调不增或单调不降,并且连续的分段函数为“凸包”(从形状上也很好理解)。
用一根直线去切这个凸包,切到一个交点就是一个答案。

但是 \(m=2\),现在切到 \(x=3\) 的点,意味着选了 \(3\) 个物品,这由图得是因为斜率太小导致的,我们把斜率拉大:
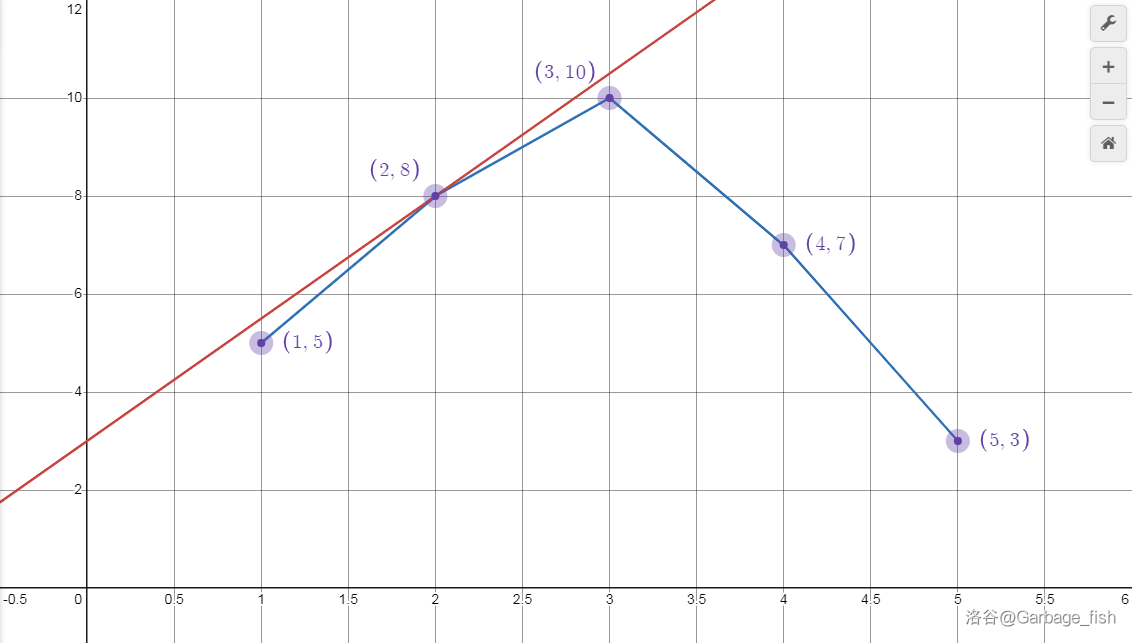
现在就切到 \(x=2\) 的位置了。
所以我们可以二分斜率,那怎么知道切到了哪个点呢呢?观察下面这两条斜率相同的直线:

会发现在凸包上只切到一个点的直线,截距(即一次函数的 \(b\))最大,而 \(b=y-kx\),所以让每个物品都减去斜率,然后直接贪心的取,统计取了多少个数,再调整斜率即可。
最后找到答案时,由于减去了 \(nk\),所以要加回来这么多的答案,理解了这个就可以做这几题。
1. P2619 [国家集训队] Tree I
对白边的边权做 WQS 二分。
2. P5633 最小度限制生成树
对给定点连的边的边权做 WQS 二分。
3. CF739E Gosha is hunting
对一种球直接 dp,另一种球做 WQS 二分。
二、Slope trick
参考资料:https://codeforces.com/blog/entry/77298。
从上面的 WQS 二分部分,我们一定已经清楚了凸包是什么。
1. 拐点维护凸包法
首先将斜率变化的点称作“分界点”,定义一种凸包表示法:将 \(f(x)\) 拐点的横坐标从小到大放进一个可重集合 \(S_f\) 里,在一个拐点处斜率若变化了 \(k\),则在可重集出现 \(k\) 次。
凸包 \(f(x)=|x|\) 的分界点的横坐标是 \(0\),在这个分界点,它的斜率变化了 \(2\)(即 \(1-(-1)=2\))。所以将这个函数表示为 \(S_f=\{0,0\}\)。
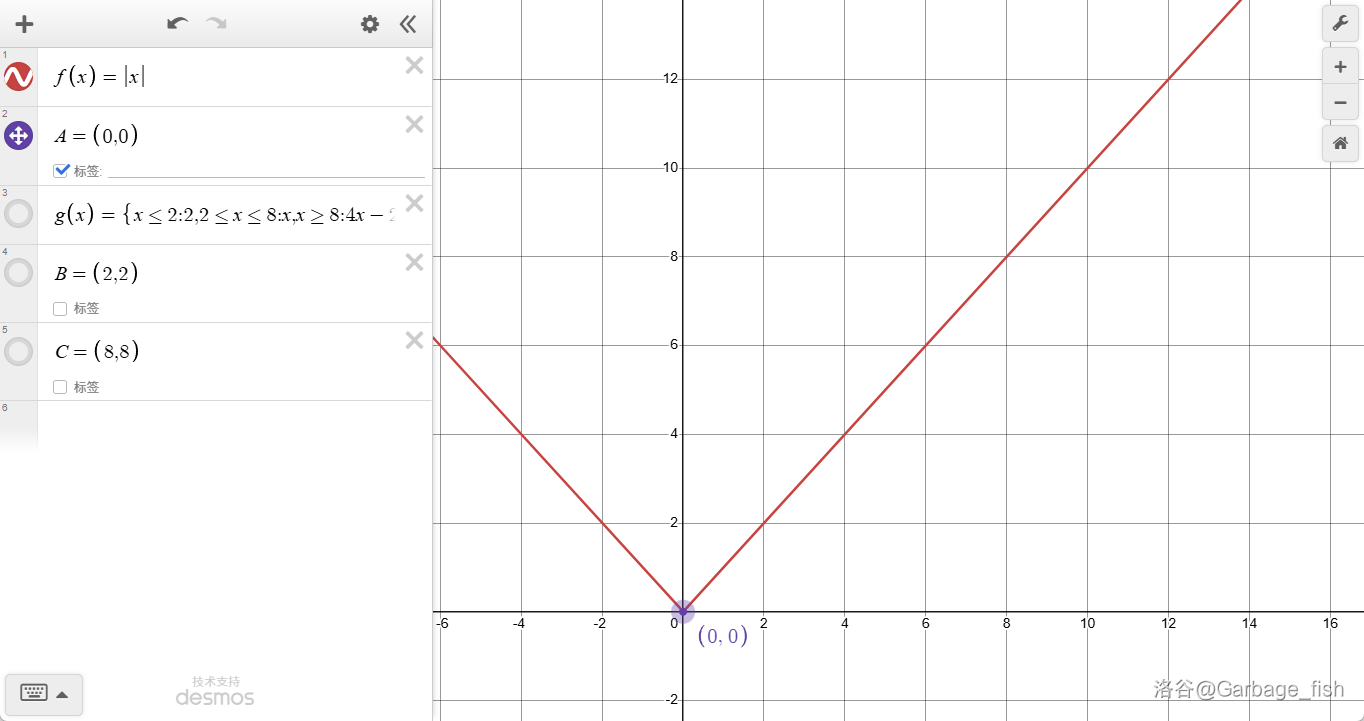
再比如这个凸包:
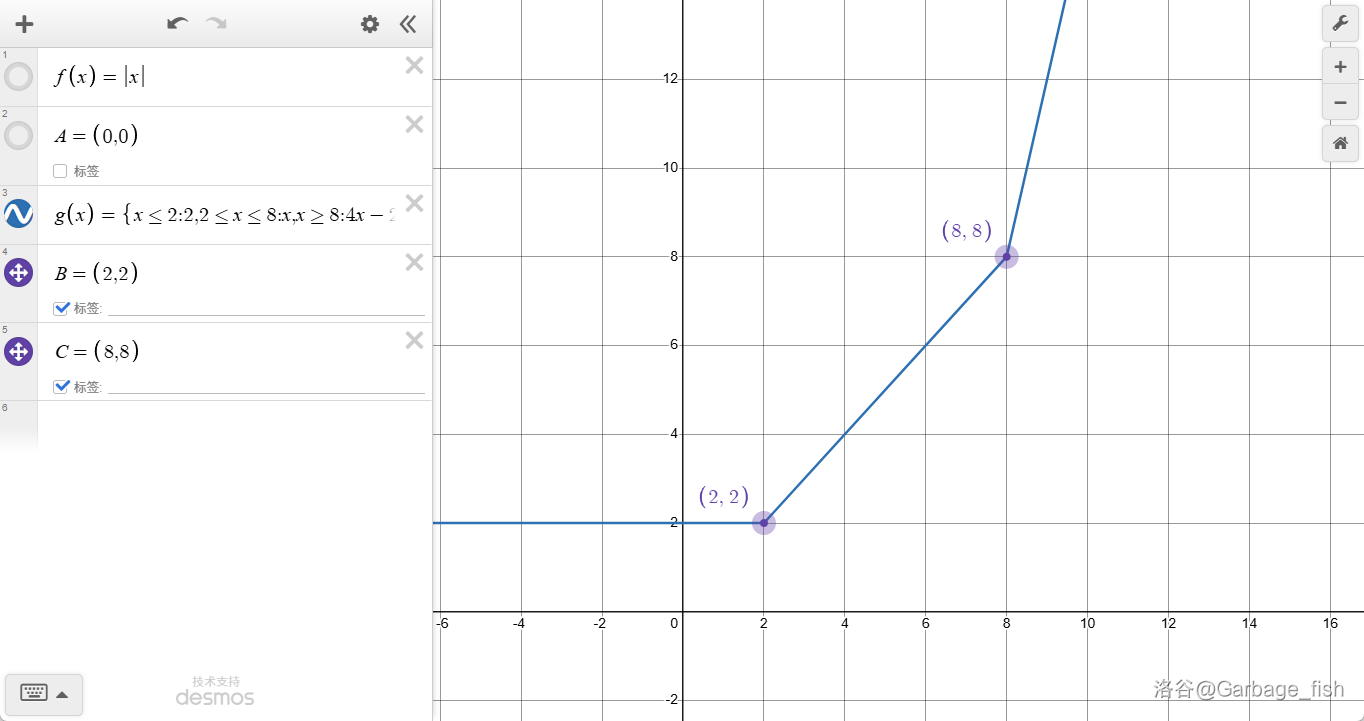
第一个分界点横坐标为 \(2\),斜率变化了 \(1\);第二个分界点横坐标为 \(8\),斜率变化了 \(3\),故 \(S_g=\{2,8,8,8\}\)。
使用这种表示法还有一个好处,只需要知道任意一段的函数表达式,就可以求得每一段的函数表达式,并且方便的得到每一段的斜率。
1.5 阅读下文须知
如果下文中提到一个点的斜率 / 截距,指这个点所在直线的斜率 / 截距。
对于拐点,则指拐点右侧的直线。因为“拐点所在直线”是一个未定义行为。
2. 凸包基本操作
(1). 两凸包相加
如果 \(f(x),g(x)\) 是同种凸包,则 \(h(x)=f(x)+g(x)\) 也是一个凸包。证明不会但是比较显然吧……
因此拐点集合合并:\(S_h=S_f\cup S_g=\{0,0,2,8,8,8\}\),每一段的 \(k,b\) 相加,但是根据上文只维护第一段的就好了。
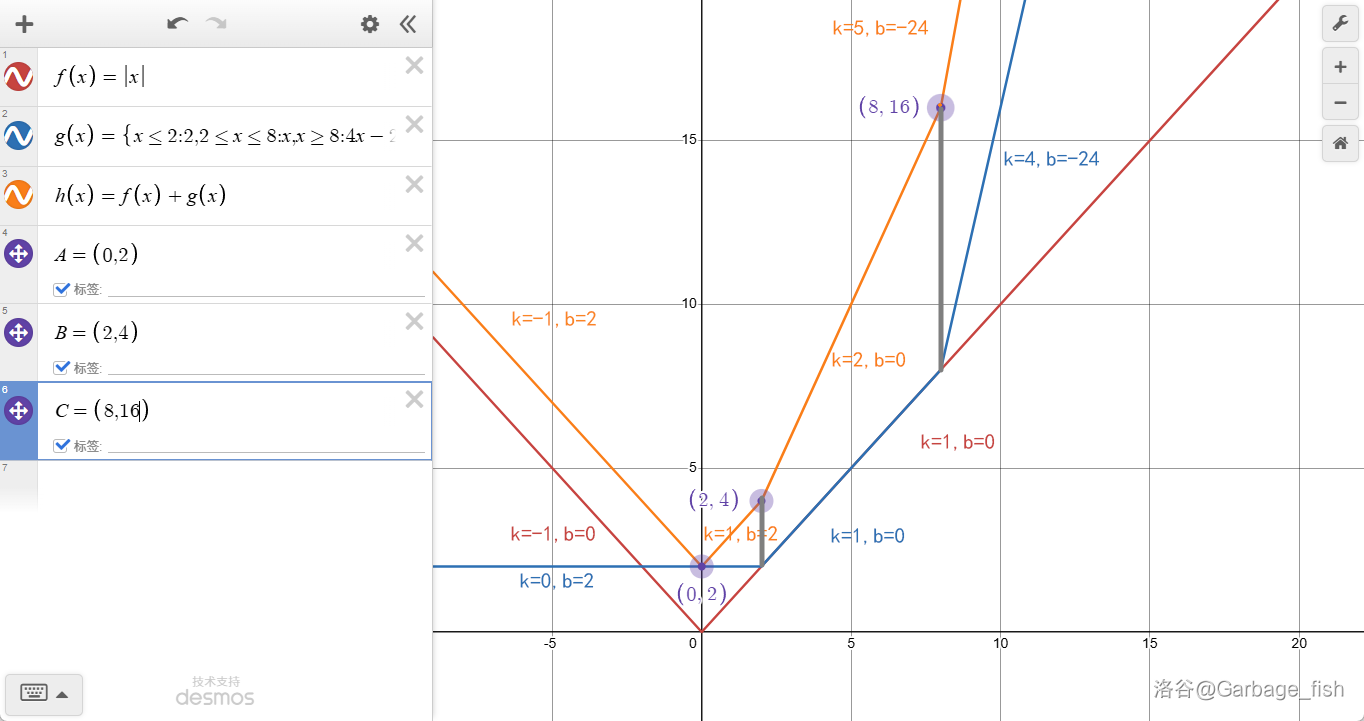
(2). 找函数最值
就是找凸包斜率为 \(0\) 的部分,用大根堆维护斜率为 \(0\) 左侧的拐点集合,小根堆维护斜率为 \(0\) 右侧的拐点集合,始终保证大根堆内元素个数不超过第一段函数的斜率的绝对值(\(|k|\))即可。超过了就往小根堆里扔,达不到就从小根堆里拿。
(3). 平移
假设 \(f(x),a(x)\) 都是凸函数,其中通常 \(f(x)\) 是我们正在维护的,而 \(a(x)\) 是容易通过题目读入等,在 \(O(1)\) 或其它较快的时间内得到的,现在要维护 \(g(x)=f(x-5)+a(x)\),把维护的 \(S_f\) 一个一个拿出来加上 \(5\) 再合并 \(a(x)\) 复杂度显然比较烂。
所以,干脆直接让坐标轴平移,如上例,让坐标轴向左平移 \(5\) 格(意思是原点不再是 \((0,0)\) 而是 \((-5,0)\),此时 \(f(x)\) 相对坐标轴的位置就等效于原坐标系中的 \(f(x-5)\)。
因此,也就不能再加上 \(a(x)\) 了,因为坐标轴的位置改变,而是要加上 \(a(x+5)\)。也就是让 \(S_a\) 中每个数减掉 \(5\) 塞进 \(S_f\) 即可。
这个减掉多少显然是可以一直往下传递的,所以要专门整个变量维护坐标轴的移动情况。需要注意的是,有时候大根堆和小根堆可能分别对应两个不同的坐标轴(下文将会提到),所以必要时需要两个变量。
(如图,改变 \(f\) 的蓝色 \(g_0\) 与黑色坐标轴的相对位置,和改变 \(a\) 的橙色 \(g_1\) 与红色“坐标轴”的相对位置,是一样的)

所以,整个变量维护坐标轴平移即可。
因此平移后还是凸包。
(4). 维护前缀 \(\min/\max\)
例如对一个下凸包 \(f(x)\) 维护 \(g(x)=\min(f(x),g(x-1))\)。
那就把小根堆里的东西全丢掉就好了,因为从小根堆开始 \(f(x)\) 递增。
因此维护后还是凸包。
(5). 维护前面某个区间取 \(\min/\max\)
例如对一个下凸包 \(f(x)\) 维护 \(g(x)=\min_{i=x-l}^{x-r}f(i)\)。
你会发现由于下凸包,所以当 \(f(x)\) 斜率小于 \(0\) 时,\(g(x+r)\) 总从 \(f(x)\) 取到最小值,即 \(g(x)=f(x-r)\);当 \(f(x)\) 斜率大于 \(0\) 时,\(g(x+l)\) 总从 \(f(x)\) 取到最小值,即 \(g(x)=f(x-l)\)。所以只要对大根堆和小根堆的“坐标轴”分别进行平移即可。
如下图是 \(l=3,r=1\) 的情况,可以发现大根堆维护的地方平移了 \(1\) 距离,而小根堆维护的地方平移了 \(3\) 距离。
因此维护后还是凸包。
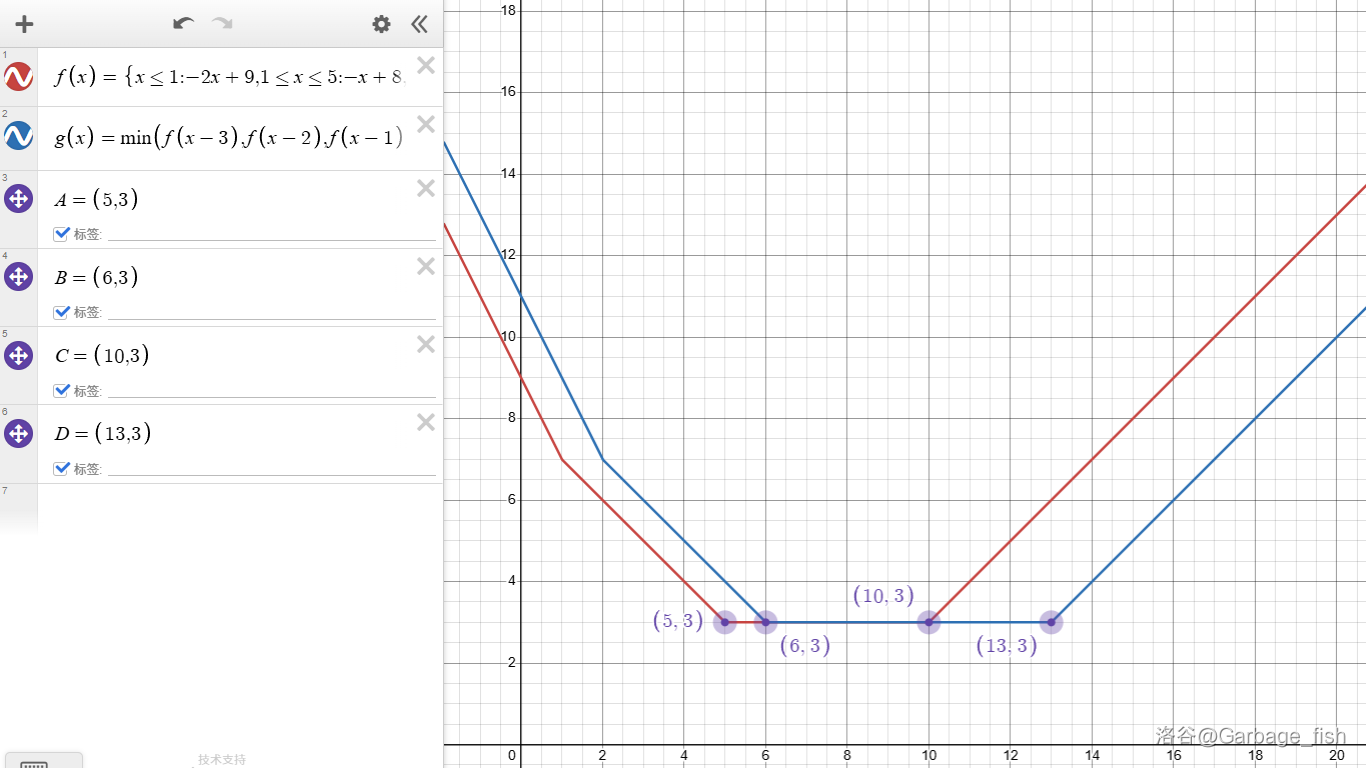
3. CF713C Sonya and Problem Wihtout a Legend
(1). 暴力求解
首先将 \(a_i\gets a_i-i\),这样就可以把严格单调递增改为求单调不降。
暴力的 dp 想法:设 \(f_i(x)\) 表示令前 \(i\) 个元素调为单调不降,且第 \(i\) 个元素至多为 \(x\) 的最小代价。设 \(g_i(x)\) 表示令前 \(i\) 个元素调为单调不降,且第 \(i\) 个元素是 \(x\) 的最小代价。答案即为 \(f_n(\infty)\)。这样子已经可以 \(O(n^3)\) dp 做出来了,但是想想 Slope trick 做法。
(2). 证明凸包
显然地,\(f_0(x)=0\),是一个凸包。
如果第 \(i\) 位想要放数 \(x\),说明第 \(i-1\) 位及以前都不大于 \(x\),而把第 \(i\) 位调到 \(x\) 的代价是 \(A_i(x)=|a_i-x|\)。故 \(g_i(x)=f_{i-1}(x)+A_i(x)\)。\(A_i(x)\) 肯定是凸包,所以,从 \(f_{i-1}(x)\) 是凸包能推到 \(g_i(x)\) 是凸包。
然后 \(f_i(x)\) 是 \(g_i(x)\) 的前缀最小值,即 \(f_i(x) = \min_{j=1}^x\{g_i(j)\}\)。对下凸包做这样的前缀最小值一定也能构成一个斜率单调递增,但斜率总不会超过 \(0\) 的凸包。所以从 \(g_i(x)\) 是凸包能推到 \(f_i(x)\) 是凸包。
所以从 \(f_0(x)\) 开始推,\(\forall i,f_i(x),g_i(x)\) 都是凸包。
然后 \(g_i(x)\) 这个凸包还有个性质:它最终一定以一条斜率为 \(1\) 的直线结尾。考虑当 \(x\ge \max_{j=1}^{i}\) 时,再怎么调大 \(x\) 前缀 \(\min\) 也不会变小, 即 \(f_{i-1}(x)\) 斜率已经归零,而 \(A_i(x)\) 的斜率还是 \(1\),所以 \(g_i(x)\) 最终的斜率会是 \(1\)。
(3). 实现凸包
每当加入函数 \(A_i(x)\),\(A_i(x)\) 的第一段函数的斜率是 \(-1\),故 \(g_i(x)\) 第一段函数的斜率的绝对值显然增加了 \(1\),因此大根堆里应该只增加 \(1\) 个元素,而 \(S_{A_i}=\{a_i,a_i\}\),因此插入到 \(S_{f_{i-1}}\) 后,将最大的弹给小根堆即可得到 \(S_{g_i}\)。而 \(f_i(x)\) 对 \(g_i(x)\) 做了一个取 \(\min\) 操作,小根堆的就被全部丢掉了,而我们实际上也并不关心 \(g_i(x)\) 的情况,他只是对求 \(f_i(x)\) 进行辅助,所以丢了就丢了。
也就是说,往 \(S_{f_{i-1}}\) 里插入两个 \(a_i\) 并弹掉最大的就能得到 \(S_{f_i}\) 了。
(4). 实现求答案
接着考虑怎么算答案,其实就是要算最后 \(f_i(x)\) 斜率归零时,它的截距时多少。
为方便记述,定义 \(m=\max\{S_{f_{i-1}}\}\),即 \(f_{i-1}(x)\) 最后一个拐点的位置,也就是大根堆的堆顶。
若 \(a_i<m\),则 \(f_i(x)\) 斜率变为 \(0\) 的位置仍会是 \(m\)。同时有 \(A_i(m)=m-a_i\),即 \(A_i(m)\) 在 \(m\) 点截距为 \(-a_i\)。而由于 \(g_i(m)=f_{i-1}(m)+A_i(m)\),假设我们已经知道了 \(f_{i-1}(m)\) 的截距(因为是递推可求的)是 \(b\),则 \(g_i(m)\) 的截距就是 \(b-a_i\)。而由于 \(f_i(m)\) 的斜率是 \(0\),所以 \(g_i(m)\) 斜率是 \(1\),故 \(f_i(m)\) 的截距就是 \(g_i(m)\) 的值,即 \(m+b-a_i\)。
也就是说,我们一直维护一个变量 \(b\),出现 \(a_i<m\) 就让它加上 \(m-a_i\) 即可。
若 \(a_i>m\),则 \(f_i(x)\) 斜率变为 \(0\) 的位置将会变为 \(a_i\)。同时有 \(A_i(a_i)=0\),即 \(A_i(a_i)\) 截距为 \(0\),所以 \(g_i(a_i)\) 的截距就是 \(f_{i-1}(a_i)\) 的截距也就是 \(f_{i-1}(m)\) 的截距(思考 \(m\) 是什么易得),所以 \(b\) 不变。
我滴任务,完成啦!!!哈哈哈哈……
4. AT_abc217_h [ABC217H] Snuketoon
什么神经分讨啊。
(1). 暴力求解
设 \(f_i(j)\) 表示第 \(i\) 个事件发生时位于 \(j\) 的最小代价。
-
\(D_i=0\):\(f_i(j)=\min_{能从j到k}f_{i-1}(k)+\max(0,X_i-j)\)。
-
\(D_i=1\):\(f_i(j)=\min_{能从j到k}f_{i-1}(k)+\max(0,j-X_i)\)。
(2). 证明凸包
看完上面那题一眼能看出这是凸包吧……\(\max\) 函数是凸包,从 \(f_0(x)\) 是凸包开始递推就能得到 \(\forall i,f_i(x)\) 是凸包。
(3). 实现凸包
其实就是第二章中操作 \(1\) 和操作 \(5\) 的结合,理解了那两个操作就没难度了。
以下是我一开始还没有系统归纳那些操作时的想法:
因为 \(T\) 实际上就是平移这个函数,整个变量维护他平移了多少就可以了,非常好搞,所以为了方便理解,讨论没有平移的情况。
对于 \(D_i=0\),有了上一题的经验,这个凸包是一个结尾斜率总为 \(0\) 的下凸包,对于 \(D_i=1\),这个凸包是一个开头斜率总为 \(0\) 的下凸包。However,\(D_i=0\) 和 \(D_i=1\) 并非独立而是混合在询问中的,所以要用大根堆维护斜率小于 \(0\) 的部分,用小根堆维护斜率大于 \(0\) 的部分。
重点讲解 \(D_i=0\) 的情况,因为另一种是同理的。
它的 \(\max\) 函数显然初始斜率为 \(-1\),截距为 \(X_i\),拐点集合为 \(\{X_i\}\) 的一个凸包,当他加到 \(f_{i-1}(x)\) 上时,\(f_i(x)\) 的初始斜率增加了 \(1\),所以大根堆内应恰好多一个数(思考大根堆是维护什么的?),如果 \(X_i\) 位于 \(f_{i-1}(x)\) 斜率变为 \(0\) 位置的左侧,直接丢进大根堆就好了,否则从小根堆里丢一个数进大根堆,再把 \(X_i\) 塞进小根堆。
(4). 实现求答案
答案就是 \(f_n(x)\) 在斜率为 \(0\) 的位置的截距。
假设 \(f_{i-1}(x)\) 在斜率为 \(0\) 的位置截距是 \(b\)。
如果 \(X_i\) 被丢到了大根堆,和上题同理,当到 \(f_{i-1}(x)\) 斜率变为 \(0\) 的位置时,\(\max(0,X_i-x)\) 函数的斜率截距都已经归零了。(思考大根堆是维护什么的?\(X_i\) 被丢到大根堆的条件?)
所以 \(f_i(x)\) 斜率变为 \(0\) 的位置截距不变,\(b\) 不变。
否则,由于 \(X_i\) 被丢到了小根堆,小根堆的堆顶就被踢到了大根堆,也就是说原本小根堆的堆顶就是 \(f_i(x)\) 斜率变为 \(0\) 的位置。
假设这个堆顶是 \(t\) 吧,那么 \(\max(0,X_i-x)\) 在 \(t\) 这点的截距显然是 \(X_i\)(取到 \(\max\) 的后半部分了)。
\(f_{i-1}(t)\) 这一点的斜率显然是 \(1\)(\(t\) 是小根堆堆顶),一条斜率为 \(1\) 的直线过 \((t,b)\)(\(t\) 同时也是 \(f_{i-1}(x)\) 斜率为 \(0\) 位置的终点),那截距就是 \(b-t\),所以 \(f_i(t)\) 的截距就是 \(b-t+X_i\)。
所以像上一题一样整个 \(b\) 不断维护大根堆堆顶的截距。
(5). 对于 \(D_i=1\)
是同理的,照着重新分析一遍即可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号