C. Peer Review

记 deg[v] 表示点 \(v\) 的度数

答案就是 \(\binom{N-1-deg[v]}{3}\)

代码实现 
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

int main() {
    int n, m;
    cin >> n >> m;
    
    vector<int> deg(n);
    rep(i, m) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        deg[a]++; deg[b]++;
    }
    
    rep(i, n) {
        ll x = n-1-deg[i];
        ll ans = x*(x-1)*(x-2)/6;
        cout << ans << ' ';
    }
    
    return 0;
}

D. Swap and Range Sum

一眼线段树
但手玩样例可以发现，只有 \(x\) 处的前缀和会发生改变，那么只需要简单微调一下即可

代码实现 
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;

int main() {
    int n, q;
    cin >> n >> q;
    
    vector<int> a(n);
    rep(i, n) cin >> a[i];
    
    vector<int> s(n+1);
    rep(i, n) s[i+1] = s[i]+a[i];
    
    rep(qi, q) {
        int type;
        cin >> type;
        if (type == 1) {
            int x;
            cin >> x;
            s[x] += a[x]-a[x-1];
            swap(a[x-1], a[x]);
        }
        else {
            int l, r;
            cin >> l >> r;
            --l;
            int ans = s[r]-s[l];
            cout << ans << '\n';
        }
    }
    
    return 0;
}

E. Laser Takahashi

用极角排序把方向映射到环上，合并同方向点为区间，查询时把“顺时针 \(A→B\)”转为“逆时针 \(B→A\)”在已排序数组上的区间长度，从而得到被激光消灭的怪物总数。

代码实现 
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

struct V {
    ll x, y; int i;
    V(ll x=0, ll y=0, int i=-1): x(x), y(y), i(i) {}
    ll cross(const V& a) const { return x*a.y - y*a.x; }
    bool up() const { return y > 0 or (y == 0 and x > 0); }
    bool operator<(const V& a) const {
        if (up() != a.up()) return up();
        return cross(a) > 0;
    }
};

int main() {
    int n, q;
    cin >> n >> q;
    
    vector<V> ps(n);
    rep(i, n) cin >> ps[i].x >> ps[i].y, ps[i].i = i;
    
    sort(ps.begin(), ps.end());
    vector<int> idx(n);
    rep(i, n) idx[ps[i].i] = i;
    
    vector<int> l(n), r(n, n-1);
    rep(i, n-1) if (ps[i] < ps[i+1]) l[i+1] = i+1; else l[i+1] = l[i];
    for (int i = n-2; i >= 0; --i) {
        if (ps[i] < ps[i+1]) r[i] = i; else r[i] = r[i+1];
    }
    
    rep(qi, q) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        swap(a, b);
        a = l[idx[a]];
        b = r[idx[b]];
        if (a > b) b += n;
        cout << b-a+1 << '\n';
    }
    
    return 0;
}

F. Diagonal Separation 2

容易发现最终合法的染色应该是下图这种模式：

1.25

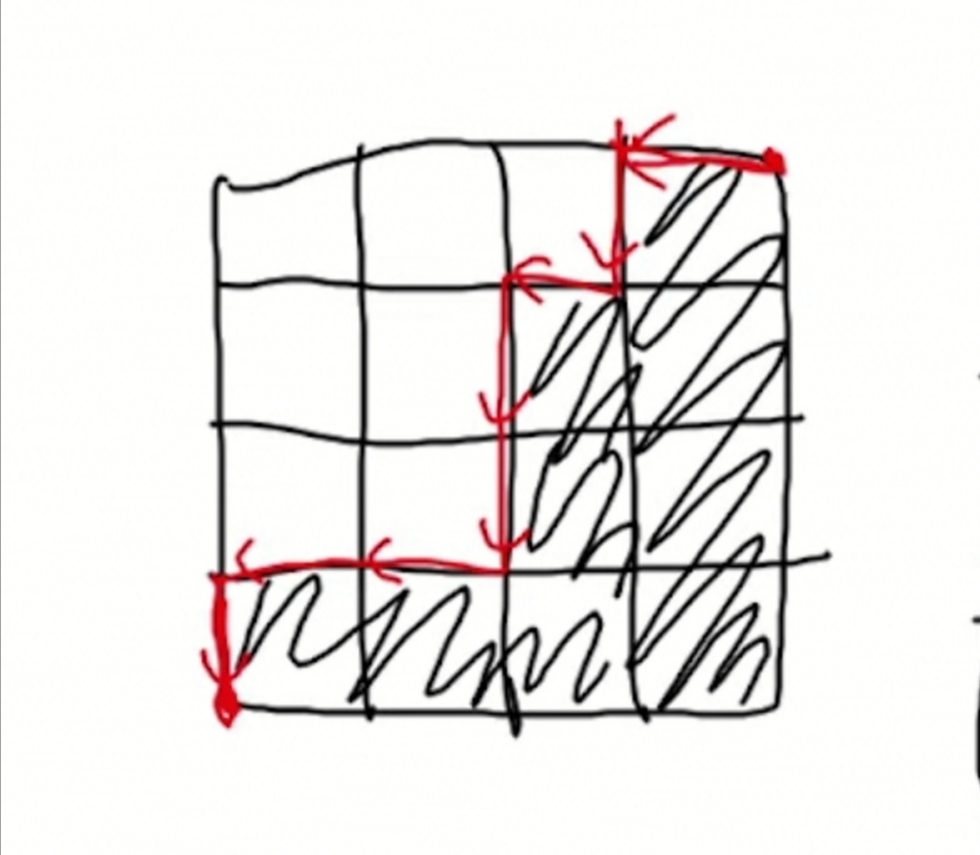
为了方便实现，可以将上下颠倒，于是就变成了左下方区域都是白色，右上方区域都是黑色

可以简单写出 \(\text{dp}\)，记 dp[i][j] 表示走到点 \((i, j)\) 时合法染色的最小费用
最后的答案就是 \(\text{dp}[N][N]\)
需要预处理一下每一行上黑色格子数的前缀和，以及每一列上白色格子数的前缀和

代码实现 
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;

inline void chmin(int& a, int b) { if (a > b) a = b; }

int main() {
    int n;
    cin >> n;
    
    vector<string> s(n);
    rep(i, n) cin >> s[n-1-i];
    
    const int INF = 1001001001;
    vector dp(n+1, vector<int>(n+1, INF));
    dp[0][0] = 0;
    
    vector cost_r(n, vector<int>(n+1));
    rep(i, n)rep(j, n) {
        cost_r[i][j+1] = cost_r[i][j] + (s[i][j] == '#');
    }
    vector cost_c(n+1, vector<int>(n));
    rep(i, n)rep(j, n) {
        cost_c[i+1][j] = cost_c[i][j] + (s[i][j] == '.');
    }
    
    rep(i, n+1)rep(j, n+1) {
        if (i < n) chmin(dp[i+1][j], dp[i][j] + cost_r[i][j]);
        if (j < n) chmin(dp[i][j+1], dp[i][j] + cost_c[i][j]);
    }
    
    cout << dp[n][n] <<'\n';
    
    return 0;
}

G. Lightweight Knapsack

如果固定选取重量为 \(1、2、3\) 的物品的个数，那么具体选哪几件可以用贪心确定。分别枚举重量为 \(1、2、3\) 的个数在 \(\bmod 6、 \bmod 3、 \bmod 2\) 下的可能值，处理好这些余数之后，剩下的就可以按每重量 \(6\) 为一组合并，所以也能用贪心处理。