ABC435

C. Domino

维护当前能推倒的右边界

代码实现

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;

int main() {
    int n;
    cin >> n;
    
    vector<int> a(n);
    rep(i, n) cin >> a[i];
    
    int ans = 0;
    int r = 0;
    rep(i, n) {
        if (i > r) break;
        r = max(r, i+a[i]-1);
        ans++;
    }
    
    cout << ans << '\n';
    
    return 0;
}

D. Reachability Query 2

建反图，从点 \(v\) 开始跑 \(\text{bfs}\) 把所有能遍历到的点都染上黑色

代码实现

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;

int main() {
    int n, m;
    cin >> n >> m;
    
    vector<vector<int>> to(n);
    rep(i, m) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        to[b].push_back(a);
    }
    
    int q;
    cin >> q;
    vector<bool> black(n);
    rep(qi, q) {
        int type, v;
        cin >> type >> v;
        --v;
        if (type == 1) {
            queue<int> q;
            auto push = [&](int v) {
                if (black[v]) return;
                black[v] = true;
                q.push(v);
            };
            push(v);
            while (q.size()) {
                int v = q.front(); q.pop();
                for (int u : to[v]) push(u);
            }
        }
        else {
            if (black[v]) puts("Yes");
            else puts("No");
        }
    }
    
    return 0;
}

E. Cover query

只需维护一个数据结构：

• 插入区间
• 删除 \([l, r]\) 里覆盖的区间

可以用 std::set 来实现，另外这实际上就是珂朵莉树

代码实现

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using P = pair<int, int>;

int main() {
    int n, q;
    cin >> n >> q;
    
    int ans = n;
    set<P> s;
    rep(qi, q) {
        int l, r;
        cin >> l >> r;
        --l;
        
        auto it = s.lower_bound(P(l, -1));
        if (it != s.begin() and prev(it)->second >= l) it--;
        while (it != s.end() and it->first <= r) {
            ans += it->second - it->first;
            l = min(l, it->first);
            r = max(r, it->second);
            s.erase(it++);
        } 
        
        s.emplace(l, r);
        ans -= r-l; 
        
        cout << ans << '\n';
    }
    
    return 0;
}

F. Cat exercise

显然每次移除猫所在的塔是最优的
一旦猫跳到某个位置就不能再往回跳了
笛卡尔树上 \(\text{dp}\)

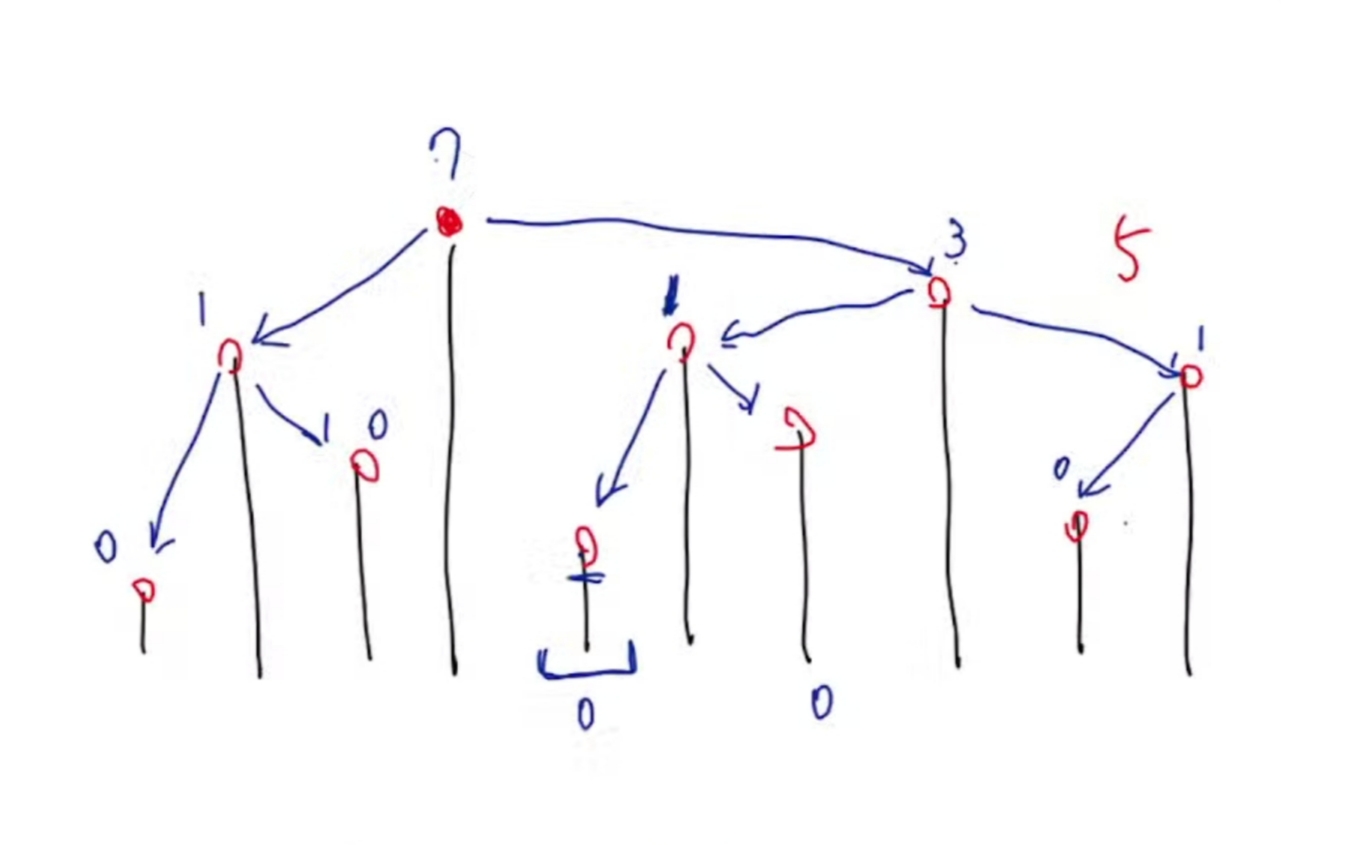
代码实现

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

template<class T=long long>
struct CartesianTree {
    int n, root;
    vector<int> l, r;
    CartesianTree() {}
    CartesianTree(const vector<T>& a, bool _max=true) {
        n = a.size();
        l = r = vector<int>(n, -1);
        vector<int> st;
        rep(i, n) {
            int p = -1;
            while (st.size() and !((a[st.back()] < a[i]) ^ _max)) { 
                int j = st.back(); st.pop_back();
                r[j] = p; p = j;
            }
            l[i] = p;
            st.push_back(i);
        }
        rep(i, st.size()-1) r[st[i]] = st[i+1];
        root = st[0];
    }
};

int main() {
    int n;
    cin >> n;
    
    vector<int> p(n);
    rep(i, n) cin >> p[i];
    
    CartesianTree t(p);
    auto f = [&](auto& f, int v) -> ll {
        int l = t.l[v], r = t.r[v];
        ll res = 0;
        if (l != -1) res = max(res, f(f, l) + (v-l));
        if (r != -1) res = max(res, f(f, r) + (r-v));
        return res;
    };
    
    cout << f(f, t.root) << '\n';
    
    return 0;
}

G. Domino Arrangement

参考 StarSilk