A. Strictly Increasing?
模拟
代码实现
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using namespace std;
int main() {
int n;
cin >> n;
vector<int> a(n);
rep(i, n) cin >> a[i];
rep(i, n-1) {
if (a[i] >= a[i+1]) {
puts("No");
return 0;
}
}
puts("Yes");
return 0;
}
B. Make Target
模拟
代码实现
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using namespace std;
int main() {
int n;
cin >> n;
vector<string> s(n, string(n, '.'));
rep(l, n) {
int r = n-1-l;
if (l > r) continue;
char c = '#';
if (l%2) c = '.';
for (int i = l; i <= r; ++i) {
for (int j = l; j <= r; ++j) {
s[i][j] = c;
}
}
}
rep(i, n) cout << s[i] << '\n';
return 0;
}
C. Shortest Duplicate Subarray
遍历同一个数的相邻两个位置差+1求最小值
代码实现
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using namespace std;
int main() {
int n;
cin >> n;
vector<int> a(n);
rep(i, n) cin >> a[i];
vector<int> cnt(1000005);
int mult = 0;
const int INF = 1001001001;
int ans = INF;
int r = 0;
rep(l, n) {
while (r < n and mult == 0) {
cnt[a[r]]++;
if (cnt[a[r]] == 2) mult++;
r++;
}
if (mult == 0) break;
ans = min(ans, r-l);
if (cnt[a[l]] == 2) mult--;
cnt[a[l]]--;
}
if (ans == INF) ans = -1;
cout << ans << '\n';
return 0;
}
D. Pigeon Swap
考虑将巢里的鸽子看成一个整体,也就是将巢里的鸽子视为放入一个袋子 \(B\) 里,然后维护以下三种映射:
- \(P \to B\)
- \(B \to H\)
- \(H \to B\)
代码实现
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using namespace std;
int main() {
int n, q;
cin >> n >> q;
vector<int> p2b(n);
vector<int> b2h(n);
vector<int> h2b(n);
rep(i, n) p2b[i] = i;
rep(i, n) b2h[i] = i;
rep(i, n) h2b[i] = i;
rep(qi, q) {
int type;
cin >> type;
if (type == 1) {
int a, b;
cin >> a >> b;
--a; --b;
p2b[a] = h2b[b];
}
else if (type == 2) {
int a, b;
cin >> a >> b;
--a; --b;
swap(h2b[a], h2b[b]);
b2h[h2b[a]] = a;
b2h[h2b[b]] = b;
}
else {
int a;
cin >> a;
--a;
int ans = b2h[p2b[a]];
cout << ans+1 << '\n';
}
}
return 0;
}
E. Flip Edge
扩展Dijkstra
第二维用来维护是否翻转
那么只需要开2倍点即可
代码实现
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using namespace std;
using ll = long long;
using P = pair<ll, int>;
int main() {
int n, m, x;
cin >> n >> m >> x;
n *= 2;
vector<vector<int>> to(n);
rep(i, m) {
int a, b;
cin >> a >> b;
--a; --b;
to[a*2].push_back(b*2);
to[b*2+1].push_back(a*2+1);
}
const ll INF = 1e18;
priority_queue<P, vector<P>, greater<P>> q;
vector<ll> dist(n, INF);
auto push = [&](int v, ll d) {
if (dist[v] <= d) return;
dist[v] = d;
q.emplace(d, v);
};
push(0, 0);
while (q.size()) {
auto [d, v] = q.top(); q.pop();
if (dist[v] != d) continue;
for (int u : to[v]) push(u, d+1);
push(v^1, d+x);
}
ll ans = min(dist[n-1], dist[n-2]);
cout << ans << '\n';
return 0;
}
F. Smooth Occlusion
注意到 \(H\) 满足单调性(\(H\) 可行,\(H-1\) 一定也可行)
费用为 \(\sum\limits_i (U_i + D_i) - H \times N\),可以看出 \(H\) 越大,费用越小
我们可以二分出满足条件的最大的H
代码实现
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using namespace std;
using ll = long long;
int main() {
int n, x;
cin >> n >> x;
vector<int> u(n), d(n);
rep(i, n) cin >> u[i] >> d[i];
auto judge = [&](ll h) {
ll l = 0, r = h;
rep(i, n) {
ll nl = h-d[i], nr = u[i];
nl = max(nl, 0ll);
nr = min(nr, h);
nl = max(nl, l-x);
nr = min(nr, r+x);
l = nl; r = nr;
if (l > r) return false;
}
return true;
};
ll ac = 0, wa = 3e9;
while (ac+1 < wa) {
ll wj = (ac+wa)/2;
if (judge(wj)) ac = wj; else wa = wj;
}
ll ans = 0;
rep(i, n) ans += u[i]+d[i];
ans -= ac*n;
cout << ans << '\n';
return 0;
}
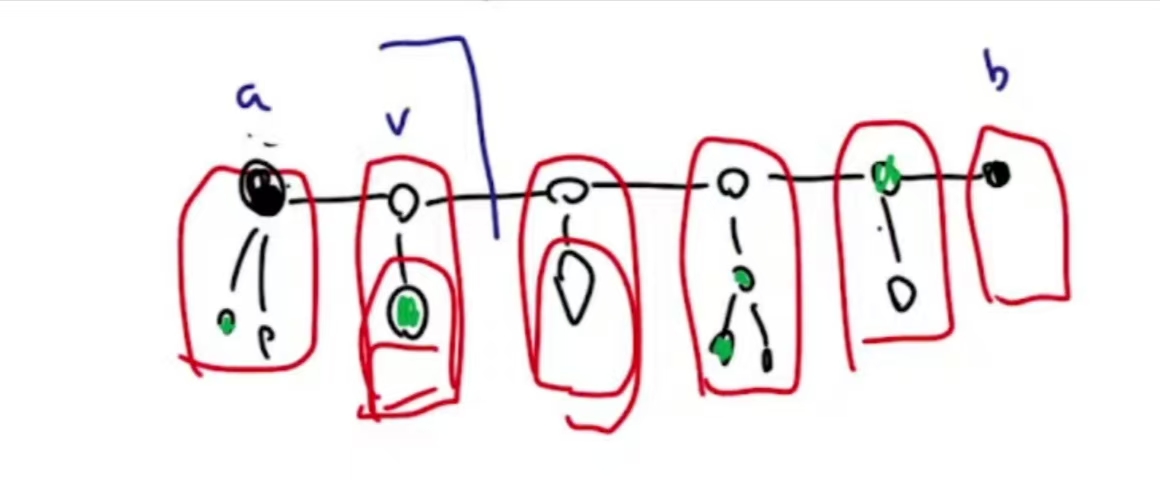
G. Minimum Steiner Tree 2
steiner树dp+flyod最短路
考虑 \(a\) 和 \(b\) 这两点间的最短路
记 dp[v][S] 表示在 \(a \to v\) 的最短路及其路径上挂着的支路中选择若干个点使得 \(a\), \(S\), \(v\) 连通的最小费用
时间复杂度为 \(\mathcal{O}(3^K \cdot N^2)\)
代码实现
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using namespace std;
using ll = long long;
inline void chmin(ll& x, ll y) { if (x > y) x = y; }
int main() {
cin.tie(nullptr) -> sync_with_stdio(false);
int n, k;
cin >> n >> k;
int k2 = 1<<k;
vector c(n, vector<ll>(n));
rep(i, n)rep(j, n) cin >> c[i][j];
rep(k, n)rep(i, n)rep(j, n) chmin(c[i][j], c[i][k]+c[k][j]);
const ll INF = 1e18;
vector dp1(n, vector<ll>(k2, INF)); // dp1[v][S]: 以 v 为根且包含点集 S 的最小费用
vector dp(n, vector(n, vector<ll>(k2, INF)));
rep(i, n) dp1[i][0] = 0;
rep(i, k) dp1[i][1<<i] = 0;
rep(s, k2) {
for (int t = s; t; t = (t-1)&s) {
rep(i, n) chmin(dp1[i][s], dp1[i][t]+dp1[i][s^t]);
}
rep(i, n)rep(j, n) chmin(dp1[i][s], dp1[j][s]+c[j][i]);
}
rep(sv, n) {
auto& ndp = dp[sv];
ndp[sv][0] = 0;
rep(s, k2) {
for (int t = s; t; t = (t-1)&s) {
rep(i, n) chmin(ndp[i][s], dp1[i][t]+ndp[i][s^t]);
}
rep(i, n)rep(j, n) chmin(ndp[i][s], ndp[j][s]+c[j][i]);
}
}
int q;
cin >> q;
rep(qi, q) {
int a, b;
cin >> a >> b;
--a; --b;
ll ans = dp[a][b][k2-1];
cout << ans << '\n';
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号