T1：Order Something Else

模拟

代码实现 
n, p, q = map(int, input().split())
d = list(map(int, input().split()))
print(min(p, q+min(d)))

T2：Strictly Superior

模拟

代码实现 
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;

int main() {
    int n, m;
    cin >> n >> m;
    
    vector<int> p(n);
    vector<vector<int>> f(n);
    
    rep(i, n) {
        int c;
        cin >> p[i] >> c;
        f[i] = vector<int>(c);
        rep(j, c) cin >> f[i][j];
    }
    
    rep(i, n)rep(j, n) if (i != j) {
        if (p[i] < p[j]) continue;
        bool ok = true;
        for (int e : f[i]) {
            if (find(f[j].begin(), f[j].end(), e) == f[j].end()) ok = false;
        }
        if (!ok) continue;
        if (p[i] == p[j] and f[i] == f[j]) continue;
        puts("Yes");
        return 0;
    }
    
    puts("No");
    
    return 0;
}

// 用 bitset 实现
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;

int main() {
    int n, m;
    cin >> n >> m;
    
    vector<int> p(n);
    vector<bitset<101>> f(n);
    
    rep(i, n) {
        int c;
        cin >> p[i] >> c;
        rep(j, c) {
            int e;
            cin >> e;
            f[i][e] = 1;
        }
    }
    
    rep(i, n)rep(j, n) if (i != j) {
        if (p[i] < p[j]) continue;
        if ((f[i]&f[j]) != f[i]) continue;
        if (p[i] == p[j] and f[i] == f[j]) continue;
        puts("Yes");
        return 0;
    }
    
    puts("No");
    
    return 0;
}

T3：Reversible

可以先给木棍确定一个方向，只考虑以某个端点开始的字典序更小的字符串
然后用 set 来维护即可

代码实现 
n = int(input())

st = set()
for _ in range(n):
    s = input()
    st.add(min(s, s[::-1]))

print(len(st))

T4：Peaceful Teams

暴力 \(\operatorname{dfs}\) 即可

从第一个选手开始，由 \(\operatorname{dfs}\) 决定进入第几个队伍，最后检查队伍数量即可

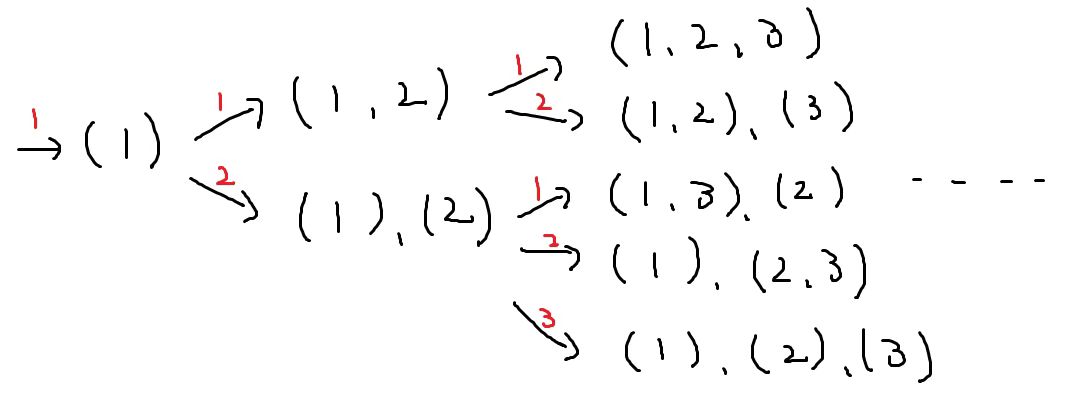
image

代码实现 
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;

int main() {
    int n, t, m;
    cin >> n >> t >> m;
    
    vector bad(n, vector<bool>(n));
    rep(i, m) {
        int a, b;
        cin >> a >> b;
        --a; --b;
        bad[a][b] = true;
        bad[b][a] = true;
    }
    
    int ans = 0;
    vector<vector<int>> team;
    auto f = [&](auto f, int i) -> void {
        if (i == n) {
            if (team.size() == t) ans++;
            return;
        }
        
        rep(j, team.size()) {
            bool ok = true;
            for (int p : team[j]) if (bad[i][p]) ok = false;
            if (!ok) continue;
            team[j].push_back(i);
            f(f, i+1);
            team[j].pop_back();
        }
        
        team.push_back(vector<int>(1, i));
        f(f, i+1);
        team.pop_back();
    };
    f(f, 0);
    
    cout << ans << '\n';
    
    return 0;
}

也可以用状压dp解决

记 dp[S][i] 表示将 \(S\) 中的所有选手分成 \(i\) 个队伍且不把性格不和的选手分到同一组的方案数

时间复杂度为 \(O(3^N T)\)

T5：NAND repeatedly

记 dp[n][k] 表示在 \(1 \leqslant i \leqslant n\) 中满足 \(f(i, n) = k\) 的 \(i\) 的个数

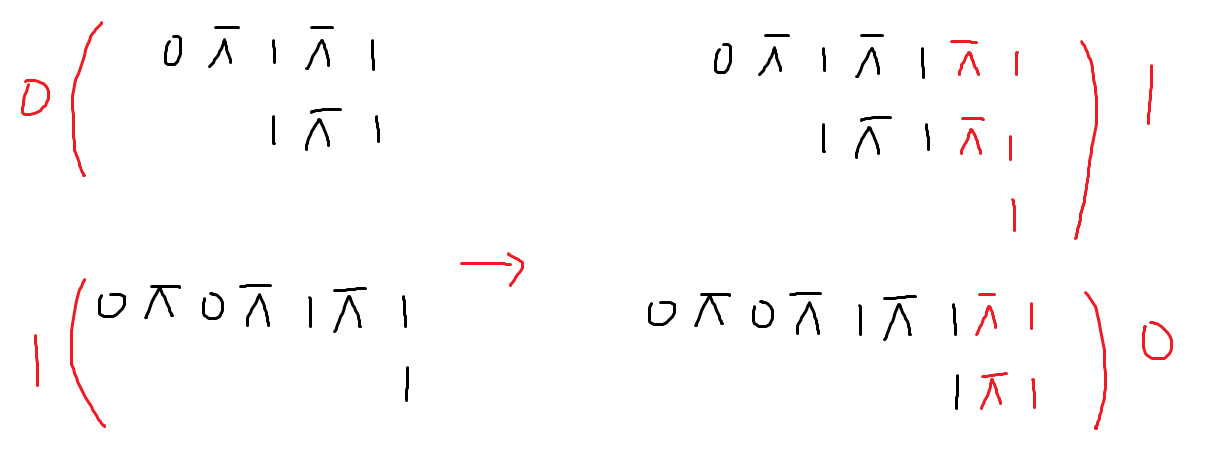
代码实现 
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

int main() {
    int n;
    string s;
    cin >> n >> s;
    
    ll ans = 0;
    vector<int> d(2);
    rep(i, n) {
        int x = s[i]-'0';
        if (x == 0) {
            d[1] += d[0]; d[0] = 0;
        }
        else {
            swap(d[0], d[1]);
        }
        d[x]++;
        ans += d[1];
    }
    
    cout << ans << '\n';
    
    return 0;
}

T6：Make 10 Again

容易发现，如果投掷出的点数大于 \(10\) 则对答案没有贡献

记 dp[i][S] 表示掷完前 \(i\) 个骰子时，能拼出集合 \(S\)（\(S\) 包含 \(0\) 到 \(10\) 的数字）的概率。

代码实现 
#include <bits/stdc++.h>
#if __has_include(<atcoder/all>)
#include <atcoder/all>
using namespace atcoder;
#endif
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using mint = modint998244353;

int main() {
    int n;
    cin >> n; 
    
    const int m = 10;
    const int m2 = 1<<(m+1);
    vector<mint> dp(m2);
    dp[1] = 1;
    rep(i, n) {
        int a;
        cin >> a;
        vector<mint> p(m2);
        swap(dp, p);
        
        rep(s, m2) {
            p[s] /= a;
            for (int x = 1; x <= min(m, a); ++x) {
                dp[(s|s<<x)&(m2-1)] += p[s];
            }
            dp[s] += p[s]*max(0, a-m); // 对于 a >= 10 的部分不产生贡献，只有前面的 i-1 个骰子有贡献
        }
    }
    
    mint ans;
    rep(s, m2) if (s>>m&1) ans += dp[s];
    
    cout << ans.val() << '\n';
    
    return 0;
}