T1: 音乐盒

本题难度简单，\(T\) 可能很大，这样就需要转圈循环并会导致超时，可以先将 \(T\) 对所有歌曲的总时间取模，再去遍历一遍歌曲即可找到答案

代码实现 
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
 
using namespace std;
using ll = long long;
 
int main() {
	int n; 
	cin >> n;
	
	vector<ll> t(n);
	rep(i, n) cin >> t[i];
	
	ll T;
	cin >> T;
	
	ll s = 0; 
	rep(i, n) {
	    s += t[i];
	    if (s > T) { // 注意 s 可能会爆 long long，所以需要特判
	        cout << i+1 << '\n';
	        return 0;
	    }
	}
	T %= s;
	
	if (T == 0) {
	    cout << n << '\n';
	    return 0;
	}
	
	rep(i, n) {
	    if (T <= t[i]) {
	        cout << i+1 << '\n';
	        return 0;
	    }
	    T -= t[i];
	}
	
	return 0;
}

T2：整数拆分

本题难度中等，双重循环枚举 \(x\) 和 \(y\) 进行判断即可拿到 \(60\) 分，对 \(f(x, y) = (x+1)(y+1) - 1\) 变形可知 \(y\) 一定是 \(10^k-1\)，\(x\) 可以是任意值，因此计算 \(y\) 的个数，然后通过乘法原理计算答案

\( f(x, y) = x \cdot y^k + y = (x+1)(y+1) - 1 \)
\( \Rightarrow x \cdot 10^k + y = xy + x + y \)
\( \Rightarrow x \cdot 10^k = xy+x \)
\( \Rightarrow 10^k = y+1 \)
\( \Rightarrow y = 10^k-1 \)

代码实现 
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

int main() {
    int m, n;
    cin >> m >> n;
    
    ll cnt = 0, y = 9;
    while (y <= n) {
        cnt++;
        y = y*10+9;
    }
    
    ll ans = cnt*m;
    cout << ans << '\n';
	
	return 0;
}

T3：龙虎斗（二）

本题难度中等，考察枚举思想与前缀和技巧。枚举分界点 \(i\)，能够发现当分界点从 \(i-1\) 移动到 \(i\) 时，左边总和增加 \(a_1 + a_2 + \cdots + a_{i-1}\)，右边总和减少 \(a_i + a_{i+1} + \cdots + a_n\)，计算这部分区间和可以使用前缀和技巧。

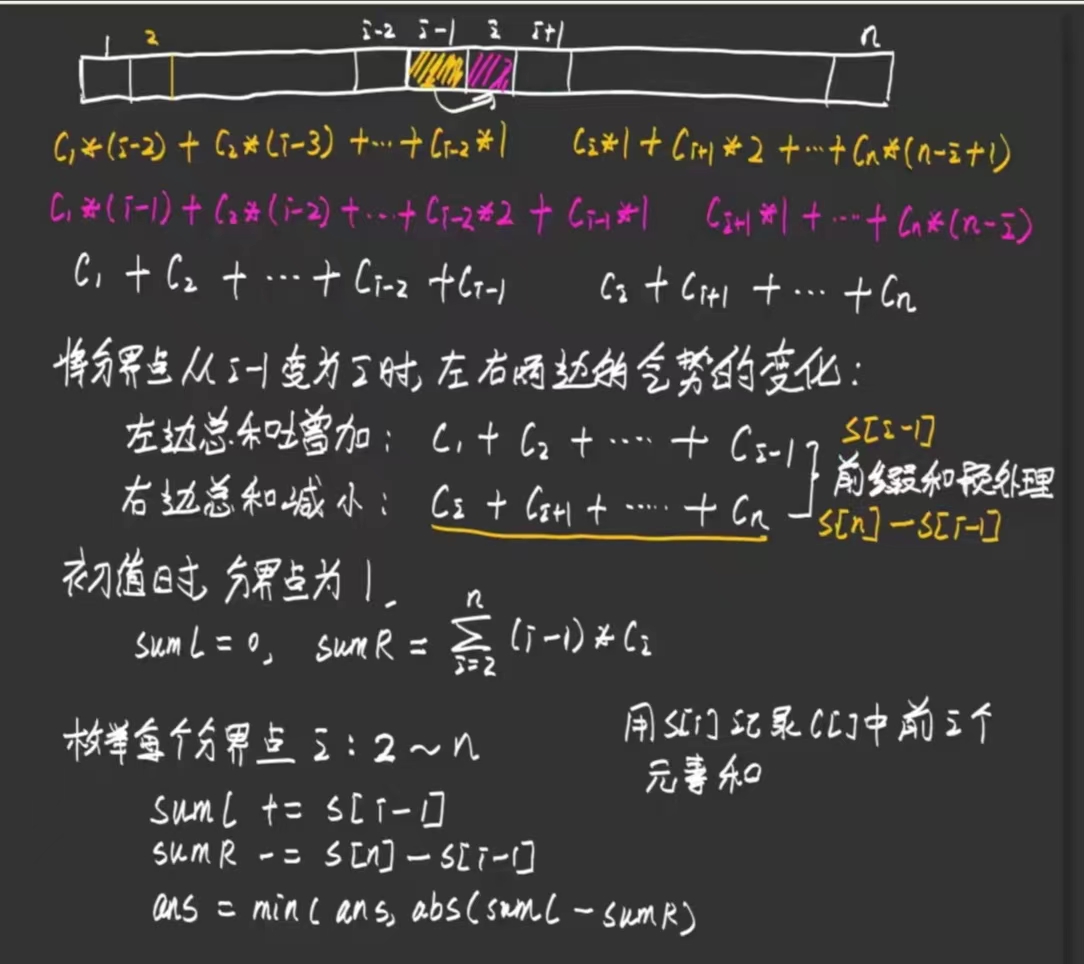
代码实现 
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

int main() {
    int n;
    cin >> n;
    
    vector<ll> c(n);
    rep(i, n) cin >> c[i];
    
    vector<ll> s(n);
    s[0] = c[0];
    for (int i = 1; i < n; ++i) s[i] = s[i-1]+c[i];
    
    ll ans = 9e18, sumL = 0, sumR = 0;
    for (int i = 1; i < n; ++i) {
        sumR += i*c[i];
    }
    ans = min(ans, sumR);
    for (int i = 1; i < n; ++i) {
        sumL += s[i];
        sumR -= s[n-1]-s[i];
        ans = min(ans, abs(sumL-sumR));
    }
    
    cout << ans << '\n';
    
    return 0;
}