T1: 水仙花指数

模拟

代码实现 
n = int(input())
ans = 0
while n != 0:
    ans += (n%10)**3
    n //= 10
print(ans)

T2：因数之和

遍历 \(i = 1, \cdots , N\)，把 \(\lfloor\frac{N}{i}\rfloor \times i\) 累加进答案

代码实现 
n = int(input())
ans = 0
for i in range(1, n+1):
    ans += (n//i)*i
print(ans)

T3：观光电梯

有若干个 \(1\)，若干个 \(2\)，若干个 \(3\)，若干个 \(4\)，我们可以把和不超过 \(4\) 的数字拼凑在一起，凑成一组队，求队数的最小值

本题考察贪心思想

  1. 我们把所有的 \(4\) 人小组，当做一队
  2. 我们去凑 \(4\) 人小组，\(1\) 和 \(3\) 凑，\(2\) 和 \(2\) 凑
    • \(3\) 人小组还有剩，剩下的每个小组就是一队
    • \(1\) 人小组还有剩，总人数/4上取整
代码实现 
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::min;
using std::vector;

int main() {
    vector<int> cnt(5);
    int x;
    while (cin >> x) cnt[x]++;
    
    int ans = cnt[4];
    // 配对
    int t = min(cnt[3], cnt[1]);
    ans += t; cnt[1] -= t; cnt[3] -= t;
    ans += cnt[2]/2; cnt[2] %= 2;
    
    if (cnt[3] == 0) ans += (cnt[1] + cnt[2]*2 + 3) / 4;
    else ans += cnt[3]+cnt[2];
    
    cout << ans << '\n';
    
    return 0;
}

T4：匹配括号（三）

匹配条件：

  1. 左括号数量等于右括号数量
  2. 对于任意一个 \(s\) 的前缀，左括号数量 \(\geqslant\) 右括号数量

背景：括号匹配问题，卡特兰数

可以用搜索的方法，暴力地寻找所有满足 \(1\) 和 \(2\) 的字符串
因为要求按照字典序，其实就是先枚举左括号，再枚举右括号
枚举的过程中当然要保证 \(2\) 是一直被满足的

dfs(l,r), 表示前 \(l+r\) 个位置已经确定，\(l\) 个左括号，\(r\) 个右括号
细节一：什么时候搜索结束？一是左括号个数等于 \(n\)，右括号个数等于 \(n\)，计数+1,如果计数达到 \(1000\)，直接结束就可以了
细节二：如果当前 l=r，下一步是左括号
细节三：如果 l=n，左括号用完了，那么下一步只能是右括号

代码实现 
#include <bits/stdc++.h>

using std::cin;
using std::cout;
using std::vector;

int n, cnt;
char s[105];
void dfs(int l, int r) {
    if (cnt >= 1000) return;
    if (l == n and r == n) {
        cnt++;
        cout << s << '\n';
    }
    else if (l == r) {
        s[l+r] = '(';
        dfs(l+1, r);
    }
    else if (l == n) {
        s[l+r] = ')';
        dfs(l, r+1);
    }
    else { // 可以使用左括号也可以使用右括号，根据字典序，先使用左括号
        s[l+r] = '(';
        dfs(l+1, r);
        s[l+r] = ')';
        dfs(l, r+1);
    }
}

int main() {
    cin >> n;
    
    dfs(0, 0);
    
    return 0;
}

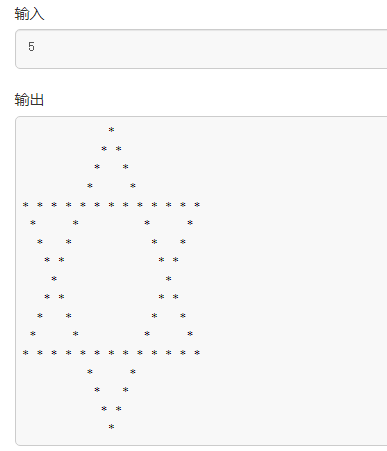
T5：打印六芒星

模拟

代码实现 
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)

using std::cin;
using std::cout;
using std::vector;

int main() {
    int n;
    cin >> n;
    // 减小工作量的办法，利用好上下对称，这是和计算机打印的特点有关，左右对称不好利用
    // 第一行，三角形的尖尖,位于 3n-2 的位置
    rep(i, 3*n-3) cout << ' ';
    cout << "*\n";
    // 第 2~n-1 行，上面这个三角形的身体
    for (int i = 2; i <= n-1; ++i) {
        rep(j, 3*n-2-i) cout << ' ';
        putchar('*');
        rep(j, 2*i-3) cout << ' ';
        putchar('*');
        puts("");
    }
    // 第 n 行，一条合在一起的边
    rep(i, 3*n-3) cout << "* ";
    cout << "*\n";
    // 接下来 n-2 行，两个三角形的身体
    rep(i, n-2) {
        rep(j, i) cout << ' ';
        putchar('*');
        rep(j, 2*(n-1-i)-1) cout << ' ';
        putchar('*');
        
        rep(j, 2*n-3+2*i) cout << ' ';
        putchar('*');
        rep(j, 2*(n-1-i)-1) cout << ' ';
        putchar('*');
        puts("");
    }
    // 两个三角形的尖尖
    rep(i, n-1) cout << ' ';
    putchar('*');
    rep(j, 4*n-5) cout << ' ';
    putchar('*');
    puts("");
    //
    for (int i = n-2; i >= 1; --i) {
        rep(j, i) cout << ' ';
        putchar('*');
        rep(j, 2*(n-1-i)-1) cout << ' ';
        putchar('*');
        
        rep(j, 2*n-3+2*i) cout << ' ';
        putchar('*');
        rep(j, 2*(n-1-i)-1) cout << ' ';
        putchar('*');
        puts("");
    }
    // 一条边
    rep(i, 3*n-3) cout << "* ";
    cout << "*\n";
    // 身体
    for (int i = n-1; i >= 2; --i) {
        rep(j, 3*n-2-i) cout << ' ';
        putchar('*');
        rep(j, 2*i-3) cout << ' ';
        putchar('*');
        puts("");
    }
    rep(i, 3*n-3) cout << ' ';
    cout << "*\n";
    
    return 0;
}