序列询问

看的 @IvanZhang2009 老师的题解，太深刻了。

考虑分治，对于每次询问，用 solve(x, y) 处理 \(x \le l \le i \le r \le y\) 的答案，其中 \(r - l + 1 \in [L, R]\)。

令区间中点为 \(mid\)，考虑 \(i \le mid\) 这一边，另一边同理，\(r \le mid\) 的会分治处理，所以考虑 \(r > mid\)。枚举 \(l\)，合法的 \(r\) 是一个区间，对于每个 \(l\) 单调队列/ST 表就行。每个 \(l\) 可以贡献到的 \(i\) 是所有 \(i \in [l, mid]\)，做一个前缀 \(\max\) 即可。

这样分治一次时间复杂度是 \(\mathcal{O}(\min(R, y - x + 1))\) 的。另外如果 \(y - x + 1 < L\) 直接停掉。

那么每次分治带个 \(\log\)，总复杂度是 \(\mathcal{O}(nq \log n)\) 的，常数有点大，应该过不去。

到这里为止这题就是一个正常的下位紫。发现不太好优化了。

考虑观察性质 DE，发现非常奇怪，那么这俩性质肯定有用。

观察 D 性质，发现每个合法的 \([l, r]\) 区间都会过中点，分治一层就结束了。观察 E 性质，两层结束。

发现了什么？

我们来画一下分治的区间，和线段树差不多：

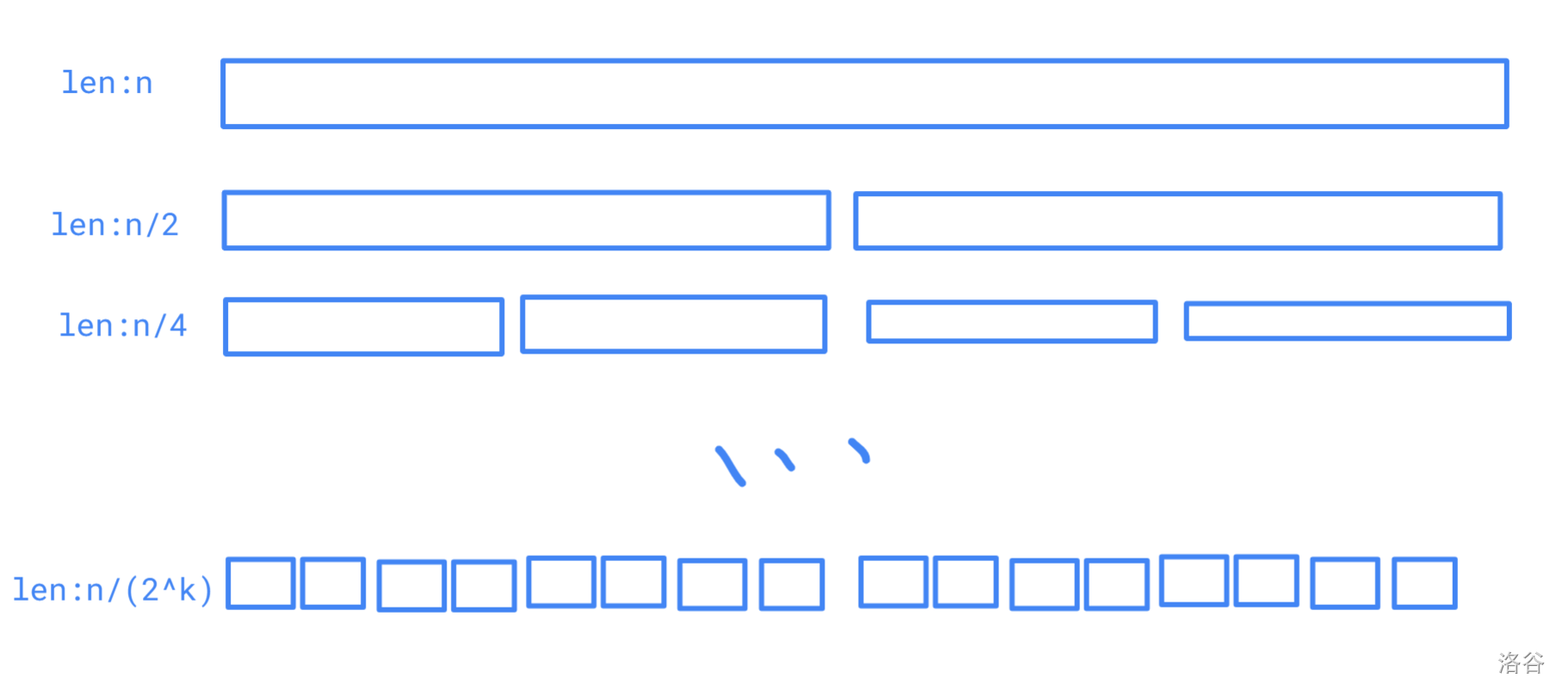
其中 \(k\) 是最大的使得 \(\frac{n}{2^k} \ge L\) 的 \(k\)。

每层的区间个数有一个性质：第 \(t\) 层 \(2^{t-1}\) 个，前 \(t\) 层一共 \(2^{t}-1\) 个。第 \(k\) 层的区间有 \(\mathcal{O}(\frac{n}{L})\) 个，由于前 \(k - 1\) 层的区间个数不超过第 \(k\) 层的区间个数，所以前 \(k\) 层的区间一共有 \(\mathcal{O}(\frac{n}{L})\) 个。

正常的分治是用 \(\sum\limits_{x, y} y - x + 1\) 计算复杂度的，每层 \(\sum y - x + 1 = n\) 故复杂度为 \(\mathcal{O}(n \log n)\)。

另外地，如果计算一个区间的复杂度有下界，那么也可以是区间个数 \(\times\) 下界，本题中下界为 \(R\)。这种方式算出来是 \(\mathcal{O}(\frac{n}{L}R)\) 的。

当 \(\frac{R}{L} = \mathcal{O}(1)\) 时，分治的复杂度是 \(\mathcal{O}(\frac{n}{L}R) = \mathcal{O}(n)\) 的。线性分治神奇不？？

接下来就需要凑出这样的 \(L, R\) 了。观察到 \([L, R]\) 拆成若干区间后每个区间分别处理没有问题，所以我们可以拆成若干个 \(L' = 2^i, R' = 2^{i + 1} - 1\)，这样的分治是线性的，就像分块一样，散块直接暴力分治，整块可以预处理即可。

时间复杂度 \(\mathcal{O}(n \log^2 n + n \log n \log\log n + nq)\)。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
// typedef __int128 i128;
typedef pair<int, int> pii;
const int N = 5e4 + 10, mod = 998244353;
const ll inf = 1e18;
template<typename T>
void dbg(const T &t) { cout << t << endl; }
template<typename Type, typename... Types>
void dbg(const Type& arg, const Types&... args) {
    cout << arg << ' ';
    dbg(args...);
}
namespace Loop1st {
int n, Q, a[N], L, R;
ll s[N], mx[17][N], mn[17][N], f[17][17][N], tmp[N], res[N], ans[N];
ll ask1(int l, int r) {
    int x = __lg(r - l + 1);
    return min(mn[x][l], mn[x][r - (1 << x) + 1]);
}
ll ask2(int l, int r) {
    int x = __lg(r - l + 1);
    return max(mx[x][l], mx[x][r - (1 << x) + 1]);
}
void solve(int l, int r) {
    if (r - l + 1 < L) return ;
    if (l == r) {
        ans[l] = max(ans[l], (ll)a[l]);
        return ;
    }
    int mid = (l + r) >> 1;
    solve(l, mid); solve(mid + 1, r);
    ll mx = -inf;
    for (int i = max(mid - R + 2, l); i <= mid; i++) {
        int x = max(mid + 1, i + L - 1), y = min(r, i + R - 1);
        if (x > y) { ans[i] = max(ans[i], mx); continue; }
        mx = max(mx, ask2(x, y) - s[i - 1]);
        ans[i] = max(ans[i], mx);
    }
    mx = -inf;
    for (int i = min(r, R + mid - 1); i > mid; i--) {
        int x = max(l, i - R + 1), y = min(mid, i - L + 1);
        if (x > y) { ans[i] = max(ans[i], mx); continue; }
        mx = max(mx, s[i] - ask1(x - 1, y - 1));
        ans[i] = max(ans[i], mx);
    }
}
void main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i], s[i] = s[i - 1] + a[i];
    for (int i = 1; i <= n; i++) mx[0][i] = mn[0][i] = s[i];
    for (int d = 1; d < 17; d++) for (int i = 0; i <= n - (1 << d) + 1; i++) { // s[0] = 0 也要考虑
        mx[d][i] = max(mx[d - 1][i], mx[d - 1][i + (1 << d - 1)]);
        mn[d][i] = min(mn[d - 1][i], mn[d - 1][i + (1 << d - 1)]);
    }
    for (int d = 0; d <= __lg(n) - 1; d++) {
        for (int i = 1; i <= n; i++) ans[i] = -inf;
        L = 1 << d, R = (1 << d + 1) - 1;
        solve(1, n);
        for (int i = 1; i <= n; i++) f[d][d][i] = ans[i];
    }
    for (int d1 = 0; d1 <= __lg(n) - 1; d1++) {
        for (int d2 = d1 + 1; d2 <= __lg(n) - 1; d2++) {  
            for (int i = 1; i <= n; i++) f[d1][d2][i] = max(f[d1][d2 - 1][i], f[d2][d2][i]);
        }
    }
    cin >> Q;
    while (Q--) {
        int l, r; ull Ans = 0; cin >> l >> r;
        for (int i = 1; i <= n; i++) ans[i] = res[i] = -inf;
        if (l * 2 > r) {
            L = l, R = r;
            solve(1, n);
            for (int i = 1; i <= n; i++) Ans ^= ans[i] * i;
            cout << Ans << '\n';
            continue;
        }
        int d1 = __lg(l) + 1, d2 = __lg(r);
        if (d1 < d2) for (int i = 1; i <= n; i++) res[i] = f[d1][d2 - 1][i];
        L = l, R = (1 << d1) - 1;
        solve(1, n);
        for (int i = 1; i <= n; i++) res[i] = max(res[i], ans[i]);
        L = 1 << d2, R = r;
        for (int i = 1; i <= n; i++) ans[i] = -inf;
        solve(1, n);
        for (int i = 1; i <= n; i++) {
            res[i] = max(res[i], ans[i]);
            Ans ^= res[i] * i;
        }
        cout << Ans << '\n';
    }
}

}
int main() {
    // freopen("data.in", "r", stdin);
    // freopen("data.out", "w", stdout);
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    int T = 1;
    // cin >> T;
    while (T--) { Loop1st::main(); }
    return 0;
}