双序列拓展

很巧妙的题。

以下内容参考了 @liangbowen 的题解。

首先明白题目的限制条件就是 \(\forall 1 \le i \ge 10^{100} f_i > g_i\) 或 \(\forall 1 \le i \ge 10^{100} f_i < g_i\)，两边只要判断一边即可，另一边只需要 \(x, y、n, m\) 互换再判断即可.
我们来考虑前者，还是可以转化成图论问题思考:

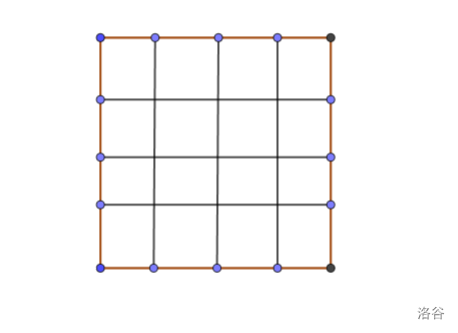
如图，横坐标表示当前匹配到的是 \(X_i\)，纵坐标表示当前匹配的是 \(Y_i\).
题目相当于是说我们当前匹配到了 \((1, 1)\)（若 \(X_1 \ge Y_1\) 就直接倒闭了），要走到 \((n, m)\)（即匹配完所有），是否可行，每次匹配，如果匹配到了 \((i, j)\)，若 \(X_i<Y_{i+1}\)，则可以走到 \((i,j+1)\)，\(X_{i+1}<Y_i\)，则可以走到 \((i+1,j)\)，\(X_{i+1}<Y_{i+1}\)，则可以走到 \((i+1,j+1)\).形式化地，记 \(A_{i, j}=[X_i < Y_i]\)，若走到了 \((i, j)\)，且 \(A_{i+0/1,j+0/1} = 1\)，则可以走到 \((i+0/1,j+0/1)\).
直接暴力走是 \(\mathcal{O}(nmq)\) 的，接下来考虑优化.

看到特殊性质产生联想，容易发现如果 \(X_{min} \le Y_{min}\)，则 \(Y_{min}\) 这行都是 \(0\)，是无解的.同理如果 \(X_{max} \ge Y_{max}\)，那么 \(X_{max}\) 这列都是 \(0\)，也无解.

如果过了以上特判，那么特殊性质的图就有了一个强大的性质:

\(\forall 1 \le i \ge m, A_{n,i} = 1\)
\(\forall 1 \le i \ge n, A_{i, m} = 1\)

那么图上就多了两条线，线上的点都是 \(1\).如图所示

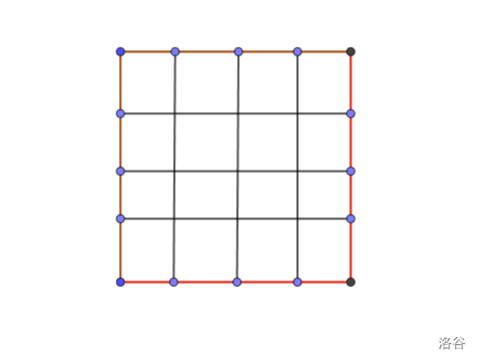
此时由于我们的目的是走到 \((n,m)\)，而走到线上任意一个点都可以走到 \((n,m)\)，所以我们只要走到线上即可，又有走到第 \(n-1\) 列或 第 \(m-1\) 行就能走到线上，所以题目的要求缩小成了走到第 \(n-1\) 列或 第 \(m-1\) 行。

由特殊性质的启发，我们想到去寻找这两条线，然后判断是否能从 \((1, 1)\) 走到线上，并从线上走到 \((n, m)\) 即可，那么就是递归求解，每次寻找前缀/后缀最大值的位置就行了，并且这样肯定是更优的。

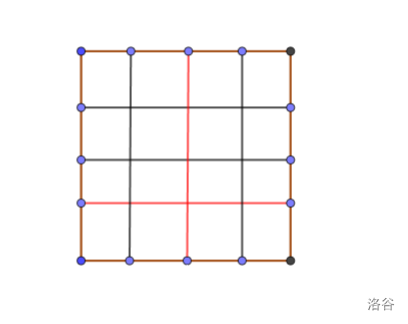
时间复杂度 \(\mathcal{O}((n+m)q)\).

Code:

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10, mod = 998244353;
typedef long long ll;
typedef pair<int, int> pii;
void cmax(int &x, int y) { if (x < y) x = y; }
void cmin(int &x, int y) { if (x > y) x = y; } 
void add(int &x, int y) { x += y; if (x >= mod) x -= mod; }
void mul(int &x, int y) { x = 1ll * x * y % mod; }
template<typename T>
void dbg(const T &t) { cerr << t << endl; }
template<typename Type, typename... Types>
void dbg(const Type& arg, const Types&... args) {
	#ifdef ONLINE_JUDGE
		return ;
	#endif
	cerr << arg << ' ';
	dbg(args...);
}   
// 由题目, 得到条件为 \forall 1 <= i <= 1e100 f[i] < g[i] 或 \forall 1 <= i <= 1e100 f[i] > g[i], 由对称性, 考虑一边即可  
// 转化成图论问题, 设 A[i][j] = [X[i] < Y[j]], 则相当于从 (1, 1) 开始, 每次往下拓展一次, e.g. 若可以走到 (i, j) 且 A[i + 1][j] = 1, 则可以走到 (i + 1, j). 问是否能走到 (n, m).
// 如果 x_min >= y_min, 则 y_min 这行都是 0, 不行, 同理如果 x_max >= y_max, 则 x_max 这列都是 0, 也不行
// 若过了这两个特判, 则只要能从 (1, 1) 走到 x_min 那列或 y_max 那行, 并能从 x_min 那列或 y_max 那行走到 (n, m) 就行了
// 找到最大最小值后，可以递归缩小范围, 详细见代码实现
// 时间复杂度 O((n + m)q)
struct Info {
	int mx, mn; //这里存的都是位置
} preX[N], sufX[N], preY[N], sufY[N];
void update(Info &A, int T[], const int &i, const Info &p) {
	A = {T[i] > T[p.mx] ? i : p.mx, T[i] < T[p.mn] ? i : p.mn};
}
int x[N], y[N], e[N], f[N], a[N], b[N];
bool check1(int x, int y) { //(1, 1) -> (x, y)
	if (x == 1 || y == 1) return true;
	Info X = preX[x - 1], Y = preY[y - 1];
	if (a[X.mn] < b[Y.mn]) return check1(X.mn, y);
	if (a[X.mx] < b[Y.mx]) return check1(x, Y.mx); //这里是在找新的红线，新红线和两条旧红线必有交点所以互相可达.
	return false;
}
bool check2(int x, int y, int n, int m) { //(x, y) -> (n, m)
	if (x == n || y == m) return true;
	Info X = sufX[x + 1], Y = sufY[y + 1];
	if (a[X.mn] < b[Y.mn]) return check2(X.mn, y, n, m);
	if (a[X.mx] < b[Y.mx]) return check2(x, Y.mx, n, m);
//同理
	return false;
}
bool solve(int tx[], int ty[], int n, int m) { //能否 f[i] < g[i]
	if (tx[1] >= ty[1]) return false;
	for (int i = 1; i <= n; i++) a[i] = tx[i];
	for (int i = 1; i <= m; i++) b[i] = ty[i];
	preX[1] = preY[1] = {1, 1}, sufX[n] = {n, n}, sufY[m] = {m, m};
	for (int i = 2; i <= n; i++) {
		update(preX[i], a, i, preX[i - 1]);
	}
	for (int i = 2; i <= m; i++) {
		update(preY[i], b, i, preY[i - 1]);
	}
	for (int i = n - 1; i; i--) {
		update(sufX[i], a, i, sufX[i + 1]);
	}
	for (int i = m - 1; i; i--) {
		update(sufY[i], b, i, sufY[i + 1]);
	}
	Info X = preX[n], Y = preY[m];
	if (a[X.mn] >= b[Y.mn] || a[X.mx] >= b[Y.mx]) return false;
	return check1(X.mn, Y.mx) && check2(X.mn, Y.mx, n, m);
}
int main() {
	int c, n, m, Q;
	scanf("%d%d%d%d", &c, &n, &m, &Q);
	for (int i = 1; i <= n; i++) scanf("%d", &x[i]);
	for (int i = 1; i <= m; i++) scanf("%d", &y[i]);
	putchar((solve(x, y, n, m) || solve(y, x, m, n)) ? '1' : '0');
	while (Q--) {
		for (int i = 1; i <= n; i++) e[i] = x[i];
		for (int i = 1; i <= m; i++) f[i] = y[i];
		int kx, ky;
		scanf("%d%d", &kx, &ky);
		while (kx--) {
			int p, v;
			scanf("%d%d", &p, &v);
			e[p] = v;
		}
		while (ky--) {
			int p, v;
			scanf("%d%d", &p, &v);
			f[p] = v;
		}
		putchar((solve(e, f, n, m) || solve(f, e, m, n)) ? '1' : '0');
	}
	return 0;
}