摘要:  深入剖析 LRU 缓存机制的核心实现,本文巧妙融合双向链表与哈希表,解锁时间复杂度为 O (1) 的高效缓存管理。从数据结构选择到代码实现,多方面解读 LRU 缓存的设计原理及其高效性。 阅读全文
深入剖析 LRU 缓存机制的核心实现,本文巧妙融合双向链表与哈希表,解锁时间复杂度为 O (1) 的高效缓存管理。从数据结构选择到代码实现,多方面解读 LRU 缓存的设计原理及其高效性。 阅读全文
 深入剖析 LRU 缓存机制的核心实现,本文巧妙融合双向链表与哈希表,解锁时间复杂度为 O (1) 的高效缓存管理。从数据结构选择到代码实现,多方面解读 LRU 缓存的设计原理及其高效性。 阅读全文
深入剖析 LRU 缓存机制的核心实现,本文巧妙融合双向链表与哈希表,解锁时间复杂度为 O (1) 的高效缓存管理。从数据结构选择到代码实现,多方面解读 LRU 缓存的设计原理及其高效性。 阅读全文
posted @ 2025-07-30 23:54
junjunyi
阅读(164)
评论(0)
推荐(0)



 使用时间复杂度为 O(log n) 的二分查找算法实现“搜索旋转排序数组”。
使用时间复杂度为 O(log n) 的二分查找算法实现“搜索旋转排序数组”。  本文设计并实现时间复杂度为 O(log n) 的算法解决:在排序数组中查找元素的第一个和最后一个位置。
本文设计并实现时间复杂度为 O(log n) 的算法解决:在排序数组中查找元素的第一个和最后一个位置。 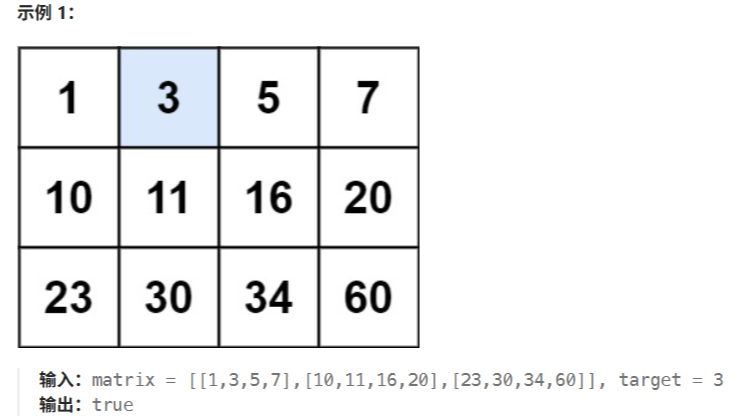 使用二分查找算法和Java代码实现:给定一个有序矩阵和一个目标值 target,确定这个值是否存在于矩阵中
使用二分查找算法和Java代码实现:给定一个有序矩阵和一个目标值 target,确定这个值是否存在于矩阵中 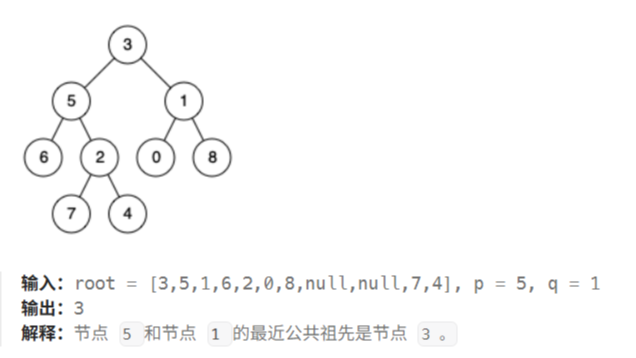 本文使用递归法找到给定二叉树中两个指定节点的最近公共祖先,给出算法步骤和Java代码的实现。
本文使用递归法找到给定二叉树中两个指定节点的最近公共祖先,给出算法步骤和Java代码的实现。  题目:给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。 路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。 核心思想: 这个问题的核心思想是深度优先搜索(DFS)
题目:给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。 路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。 核心思想: 这个问题的核心思想是深度优先搜索(DFS) 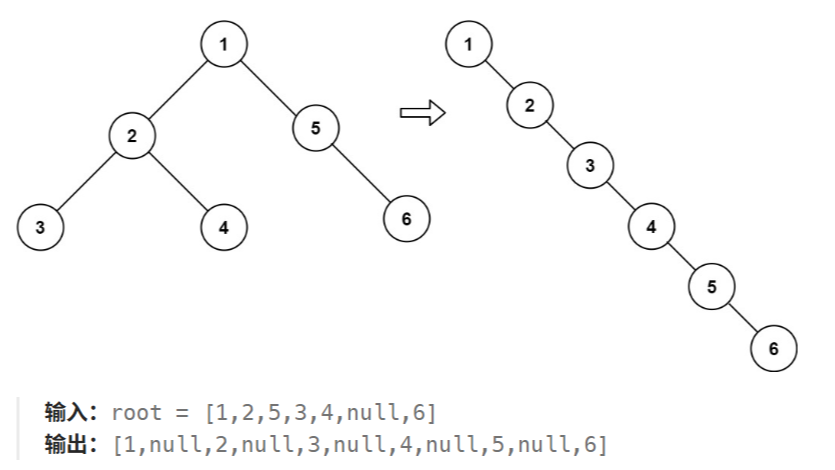 本文利用莫里斯遍历的思想,使用原地算法将二叉树展开为单链表,实现O(1)的空间复杂度。
本文利用莫里斯遍历的思想,使用原地算法将二叉树展开为单链表,实现O(1)的空间复杂度。  浙公网安备 33010602011771号
浙公网安备 33010602011771号