【LeetCode 236】算法:二叉树的最近公共祖先
题目:给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
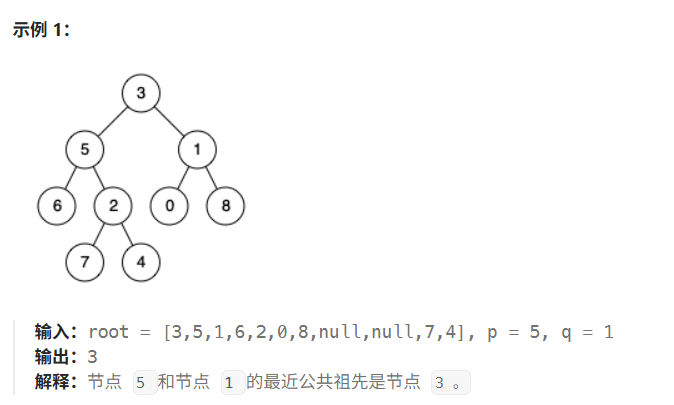
核心思路:
要找到给定二叉树中两个指定节点的最近公共祖先,可以使用递归的方法。基本思路是从根节点开始遍历树,检查每个节点是否同时包含目标节点 p 和 q。如果找到这样的节点,那么它就是 p 和 q 的最近公共祖先。
算法步骤:
- 递归终止条件:如果当前节点为空,返回 null。
- 检查根节点:如果当前节点是 p 或 q 之一,直接返回该节点,因为它是 p 和 q 的祖先。
- 递归搜索:分别在左子树和右子树中递归搜索 p 和 q。
- 合并结果:
如果 p 和 q 分别在左子树和右子树中找到,说明当前节点 root 是它们的最近公共祖先。
如果 p 和 q 都在左子树或右子树中找到,那么该子树的返回值就是 p 和 q 的最近公共祖先。 - 返回结果:根据上述逻辑返回找到的最近公共祖先。
复杂度分析:
-
时间复杂度是 O(N),其中 N 是树中节点的数量,因为每个节点最多被访问一次。
-
空间复杂度是 O(H),其中 H 是树的高度,这是由于递归调用的深度导致的。
Java代码实现:
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// 如果根节点为空,直接返回null
if (root == null) {
return null;
}
// 如果根节点正好是p或q之一,那么它就是最近公共祖先
if (root == p || root == q) {
return root;
}
// 递归地在左子树和右子树中查找p和q
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
// 如果左子树和右子树都找到了p和q,那么当前节点就是最近公共祖先
if (left != null && right != null) {
return root;
}
// 如果只在一个子树中找到,那么那个子树的结果就是答案
return left != null ? left : right;
}
}
所有正文内容皆为本人原创,禁止搬运


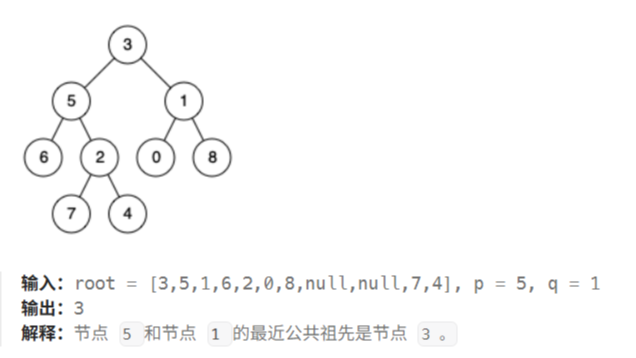 本文使用递归法找到给定二叉树中两个指定节点的最近公共祖先,给出算法步骤和Java代码的实现。
本文使用递归法找到给定二叉树中两个指定节点的最近公共祖先,给出算法步骤和Java代码的实现。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号