韬钤录 1
\(\boldsymbol{[2025/04/27]}\)
CF671D
可并堆:\(d_{x}=d_{rs}+1\),交换以保持 \(d_{rs}<d_{ls}\)。标记在递归合并儿子前,在 pop 合并左右儿子前都需要下传。
线性规划对偶:标志:较简单的不等约束。在网络流中比较常见,如 ABC397G。像这题就是每条边至少覆盖一次的约束,去做对偶。
\(\boldsymbol{[2025/04/28]}\)
D
\(\bmod 2^{32/64}\) 相关无法求逆元:可以对一个数拆成 \(a2^b(2\nmid a)\) 处理,这时候 \(a\) 求逆,\(b\) 做加减法,可以在 noip2022 T4 比赛 中应用,虽然复杂度要差一点。
有时候如果确定要 \(/x\) 可以先把 \(\bmod\times x\),求完再 \(/x\) 即可。
P10539
交互时候可以通过交互出一些模小数的信息,CRT 还原大数,如 CF1299E。
P12371
最大独立集:常见的求最大独立集的乱搞是尝试删度数最大的点。对于这个题,若 \(\deg \le 2\),每个联通块都只是环和链,单独算一下。否则暴力递归。
复杂度 \(T(n)=T(n-1)+T(n-4)\Rightarrow T(n)\sim 1.3803^n\),吊打 \(O(2^{n/2})\) 的 std。
而且空间也是 \(O(n)\) 而非 std 的 \(O(2^{n/2})\)。
虽然复杂度可能要 \(\times n\),但是根本跑不满,还可以过程中通过位运算优化只算有效位,跑得飞快。
\(\boldsymbol{[2025/04/29]}\)
P9165
拉插存储信息,可还原性高。和 CRT 一起记忆一下,数论在非传统题中的一大应用。
\(\boldsymbol{[2025/05/01]}\)
王国
树形联通块的信息可以用点减边容斥做。
\(\boldsymbol{[2025/05/07]}\)
Ena 的曲绘
做计数题还是要多摸摸小情况,不应该在一条道路上死磕,及时换思路。这题死磕分圆多项式导致了坠机。
\(\boldsymbol{[2025/05/08]}\)
qoj 10350
不联通 \(=\exp\) 联通,联通 \(=\ln\) 不联通。这是常见的联通不联通转化的方法,看哪个好算。
对于结构 \(G\),只需要支持 \(x+y,C\times x,x\times y\),其中 \(x,y\in G,C\) 为常量。就能用这个结构替换整数做 FWT,多项式运算,IFWT 这个过程。
这里结构 \(G\) 为 \(\bmod p\) 多项式循环卷积。多项式运算包括:乘、逆、\(\ln,\exp\)、快速幂等。
若需要很多次多项式乘法,可以在最开始先把所有用到的多项式 DFT 一遍,然后由于线性性,中间把乘法当成点值点乘、加减操作不便继续做,最后 IFWT 一下。
这样中间过程复杂度只需要额外多乘 \(n(\deg)\),开头的开销要 \(n^2\) 或 \(n\log n\)。适用于开尾计算量少,中间计算量多的情况。
这里多项式一般为 \(k\) 进制下 \(\text{xor}\) 卷积或者模意义下循环卷积。不然可能乘的过程中次数爆了就不能这样做了。
最终做到 \(O(n^32^n)\),假设 \(n,p\) 同阶。std 由于没用 \(\ln -\exp\) 的转化于是是 \(O(n3^n)\) 的。
\(\boldsymbol{[2025/05/09]}\)
P5999
连续段 dp:插入 dp 的时候可以尝试维护连续段的一些信息,并且做一些钦定。
在 P9197,gym102538H 中亦有记载。
\(\boldsymbol{[2025/05/10]}\)
gird
这种整体平移 \(\text{xor}\) 可以考虑多项式(虽然这题没啥用),比如 \(f(x,y)\times (x+x^{-1}+y+y^{-1}+1)\) 就代表一次操作,其中乘法 \(\bmod 2\)。
并且 \((x+x^{-1}+y+y^{-1}+1)^2=x^2+x^{-2}+y^2+y^{-2}+1\) 于是 \((x+x^{-1}+y+y^{-1}+1)^{2^k}\) 能特殊算。
\(\boldsymbol{[2025/05/11]}\)
P6782
类似 vEB 树的,考虑 \(\bf{sqrt}\) 叉树,我们就递归三层,就能做到 \(O(\sqrt[3] n)\) 单点加,\(O(1)\) 区间和。好写又优秀。
类似树剖复杂度分析的,令 \(B=\sqrt n\),则除了所有是其父前 \(B\) 大子树的点,其余点的 \(\sum sz=O(n)\)。因为每个点每对一个点有贡献,\(sz\) 都要 \(\times (B+1)\)。
CF1707D
对于不好算的条件,要有二项式反演(大点说就是反演容斥)的敏感。
uoj 961
对于竞赛图或者比竞赛图边更多的有向图,我们几乎必定考虑缩点后图的性质,如竞赛图缩点后是链。
\(\boldsymbol{[2025/05/12]}\)
uoj 750
子集和问题在值域很小的时候,通过概率分析或者抽屉原理,能发现很容易有解。这时候可以折半随机化(或直接)构造。
\(\boldsymbol{[2025/05/13]}\)
qoj 5357
考虑树形 dp 到 \(u\) 的时候,注意到我们只需要记录点分树根到 \(u\) 的距离即可。
然后 \(f_{u,x}\times \sum f_{v,\ge y}\to f'_{u,x+y}\),贡献系数是 \(\dbinom{x+y-1}{x-1}\),因为钦定最后一个点仍在最后。
\(\boldsymbol{[2025/05/15]}\)
AGC026D
积木类型的 dp?题可以尝试从小到大垒起来设计转移,或者还有一种 trick 就是根据大/小根笛卡尔树往下递归做。
\(\boldsymbol{[2025/05/16]}\)
范斯喆讲课——构造题
-
调整法
- 第一调整法:先构造一个方案,然后发现方案满足部分限制/存在部分问题,通过调整改进之。
- 第二调整法:有时候题目会限制某个量恰好为 \(k\)。这时可以尝试求出这个量的上下界,并证明上下界之间的数都能取到。然后从取到上界或下界的方案开始,逐步调整到给定值。
更抽象地说,这种思路实际上是估计最好情况和最坏情况,依此来推出所有中间情况。所以恰好为 \(k\) 这样的条件并不是必要的。
-
增量法:类似数归的,增量法的思想是,假设已经有了一个构造方法,将它扩展到更大的情况。例:竞赛图哈密顿回路。
-
归约法:归约法的思想是,找到构造目标的某个部分,将它先构造掉,然后就只需考虑删掉它之后的情况。例:网格构造题中的剥外壳。
gym103119B
高斯消元如果元太多,可以考虑把所有元都表示为 \(n\) 个元的线性组合,对这 \(n\) 个元高消,复杂度 \(O(n^3)\),在 这个题中亦有记载。
ACAM 上 \(fail_x\) 在 trie 树上的深度一定比 \(x\) 低。
\(n\) 个点建立的 trie 树的分叉个数是 \(O(n)\) 级别的。
并且对于一个点应该考虑他父亲的 dp 式子写方程,而不是他自己的,然后从上到下递推。
CF1311E
第二调整法例题。
\(\boldsymbol{[2025/05/17]}\)
APIO2025
BSGS 的本质上是构造 \(A=\{[0,B)\times B\}\cup [0,B-1)\),\(B=\sqrt n\)。此时 \(A+A\) 或者说 \(A-A\) 构造了一个 \([0,B^2/B(B-1)]\) 范围内的所有数。
若要找集合 \(S\) 中的两个满足条件 \(P(x,y)\) 的数,并且我们能判断一个集合 \(T\) 中是否存在俩满足条件的,代价是集合大小。此时:
-
随机化分治。
-
把 \(S\) 分成三份 \(A,B,C\),把 \(AB,BC\) 查一下,确定是哪两个组成的。把集合大小 \(\times \dfrac{2}{3}\)。
-
若确定了 \(x\in A,y\in B\),此时考虑 \(A\) 分成 \(A_0,A_1\),\(B\) 分成 \(B_0,B_1\),然后先询问 \(A\cup B_0\),确定在 \(B_{*}\) 中,然后询问 \(A_0,B_{*}\) 即可。
几何概型收敛慢,对于多测取次数 \(\max\) 这种交互题,尽量写确定性做法而非随机!
T3 这种一眼贪心题,应该坚信就是签到。敢于贪心,多写几个贪心至少能高分。
\(\boldsymbol{[2025/05/20]}\)
qoj 5359
缩减状态,默认 \(a\times b\) 矩形满足 \(a\le b\),周长 \(/2\)。
注意到 \([a\times b,a\times c]\to [a\times (b+c-1),1\times a]\),\([1\times a,1\times b]\to [1\times (a+b-1),1]\),最终只会剩下若干 \(1\times 1\) 以及每个宽最多一个的情况。注意到 \(1\times 1\) 的贡献是 \((x,2x)\),于是 \(2S-C\) 不变。考虑对加粗部分求出 \(2S-C\) 最小的 \(C\) 即可,随便 dp。
\(\boldsymbol{[2025/05/21]}\)
减半警报器类
减半警报器:把诸如 \(a_x+a_y\ge k\) 的限制 \((x,y,k)\) 拆成 \(a_x\ge \lceil\frac{k}{2} \rceil,a_y\ge \lceil\frac{k}{2} \rceil\) 这两个 \((x,\lceil\frac{k}{2} \rceil),(y,\lceil\frac{k}{2} \rceil)\) 限制。以独立 \(x,y\)。例题:gym102331F,P7603
qoj 8035,减半警报器能 \(\log^2\) 做,但是也能通过操作分块,批量处理做到单根号。
zak 警报器,太过困难我不会,能优化很多减半题的复杂度。

\(\boldsymbol{[2025/05/25]}\)
P8108
随机数据 LCS:令 \(S_x\) 表示 \(a\) 中数字 \(x\) 出现的位置从大到小排列的序列。把 \(b\) 中每个元素 \(b_i\gets S_{b_i}\),然后顺次拼接。对于新序列的 LIS 显然就是他们的 LCS。
CF1874F
考虑对不合法区间容斥,集合 \(S\) 定义为钦定的不合法区间集合。集合 \(S\) 的方案数的系数是 \((-1)^{|S|}\)。直接做区间有交不好处理。考虑建立双射抵消贡献,有交全被两两抵消了。然后对包含相离这样的树状区间结构做一个树形 dp,序列上就是区间 dp。
区间 dp 除了记区间容斥后的答案外,还记了 \(g_{l,r,x}\) 表示区间还剩 \(x\) 个数没被集合 \(S\) 内的区间覆盖,辅助转移。
\(\boldsymbol{[2025/05/26]}\)
二分图边染色,正则二分图匹配
\(\boldsymbol{[2025/05/27]}\)
取石子游戏
SG 函数多打表找规律猜一猜。
指针
路径长取模找性质:一般是找到基底,用裴蜀定理 \(\gcd\) 求一下解系在往下做。
\(\boldsymbol{[2025/05/28]}\)
qoj 4218
所有导出子图均有 \(\deg \le k\) 的点的图能划分为 \(k+1\) 个独立集。
构造:每次删任意一个极大独立集,这时候每个点的度数至少 \(-1\),最后是一个所有导出子图均有 \(0\) 度点的图,就是独立集。
\(\boldsymbol{[2025/05/29]}\)
CF848D
dp 设计一个中间状态,然后互相递推,交叉转移。
这题就设计一个 \(S\to O\to T\) 的 \(n\) 次 \(\text{mincut}=m\) 的方案数为 \(g_{n,m}\)。
P11086
先后手交替(不同策略)可以把先后手各操作一次一起看做一步,那么就少记一维谁先手了。
这题需要手摸观察到 dp 值大多沿对角线继承!然后只需要处理那些不继承的位置(有被洞邻域影响到的),其他一起算就行。
交流总结
-
可重状态如何计数(不重不漏),大体就这仨:
- 容斥
- 找代表元:比如说字典序最小的变成状态的方案
- 直接找充要条件,判定最终态是否合法,对分析出的性质计数。(也有可能要上 DFA 转移)
-
可以通过找答案下界,去排除一些一定不优的方案。从而减少状态/枚举量。
-
两个序列可以对应项交换的题(多为计数),可以先交换题目给出的序列,变成一个好看的形状,看看有啥性质。
\(\boldsymbol{[2025/05/30]}\)
LIS 模板题
拆贡献!比如贡献 \(x\) 可以拆分为 \(x\) 个 \(1\)。贡献 \(|S|^2\) 可以拆为 \(\sum\limits_{x,y} [x,y{\color{red}{\text{ in the same set}}}]\)。
k-LIS 是杨表前 \(k\) 行长度。
qoj 5402
\(k\) 进制异或线性基怎么做呢?特别是 \(k\) 非素。
插入 \(\vec{x}\) 的时候,设当前插入的是基 \(\vec{B_i}\)。
-
若 \(B_i\) 为空,则把 \(x_i\) 乘一个数变成 \(\gcd(x_i,k)\) 环上的最小值,插入。
-
否则,把 \(\vec{x},\vec{B_i}\) 的第 \(i\) 位辗转相除,得到一个 \((\vec{x},\vec{y})\) 对,其中 \(y_i=0\),把 \(x\) 放在 \(B_i\) 即可。
但同时第 \(i\) 位插入 \(x\) 的时候,要插入 \(x\times (k/\gcd(x_i,k))\),这样才能组合出域内所有数。
\(\boldsymbol{[2025/05/31]}\)
AGC013D
代表元去重:注意到一个取球序列可能对应多个取球方案,因为初始红球能减少,于是钦定只在有达到过 \(0\) 个红球的方案被计入即可。
\(\boldsymbol{[2025/06/01]}\)
P6644
APIO 讲课的增量法构造例题,增量法顾名思义,从 \(n-1\) 情况考虑构造加一个数到 \(n\) 的情况。双倍经验。
\(\boldsymbol{[2025/06/02]}\)
qoj 7991
广义串并联图缩合板子。特征:有 \(m-n\le k\),其中 \(k\) 不大这个特殊性质。
一般广义串并联图性质:
-
去掉重边后 \(m\le 2n\)。
-
广义串并联图可以通过以下的操作变成一个单点:
- 删一度点(去断路):选择一个度数为 \(1\) 的点并删掉它和与它连接的边
- 缩二度点(消串联):选择一个度数为 \(2\) 的点,用一条边替换它和与它相连的两条边(两条边缩为一条)
- 叠合重边(消并联):选择两条重边,用一条边替换它们
-
因为以上三种操作, \(m - n = k\) 的值都是不增的,同时操作后所有点的度数 \(\ge 3\),所以 \(2m \ge 3n\),又有 \(m \le n + k\),得到 \(n \le 2k, m \le 3k\)。
-
广义串并联图是平面图。
\(\boldsymbol{[2025/06/03]}\)
P12573
依然是从简单情况入手。考虑用 trie 树查询的方法,来刻画一个区间的答案。就想到了枚举 \(\min\) 对应的是哪个 \(j\),计算 \(2^d\) 在何时被贡献。
记 \(l_{x,d},r_{x,d}\) 分别是 \(x\) 的 \(d\) 儿子在 trie 树上异侧兄弟节点子树内,编号关于 \(x\) 的前驱后继。
那么当且仅当 \(l<l_{x,d}\le r_{x,d}<r\) 的时候对于 \(x\) 有 \(2^d\)。然后每个 \(x\) 对应 \(m^2\) 个本质不同区间,拎出来数点。
还有就是 \(O(nm^2)\) 空间不能存储,可以考虑对答案补集转换,这样左右端点就独立开来了,只需要 \(O(nm)\) 空间存储。
P6790
广义串并联图由于能不断通过缩一二度点和重边变成单点。于是考虑缩边的过程动态维护对应信息。
观察广义串并联图缩边后的一条边 \(u \to v\),显然对应原图的一个子图,且子图里的点除了 \(u \to v\) 以外只和 \(u/v\) 连接,因此这个子图最后的状态只有两种:\(u, v\) 连通或 \(u, v\) 不连通。
缩点/边的时候简单 dp 转移即可。
另一道例题:Grand Graph。
\(\boldsymbol{[2025/06/04]}\)
P10046
绝对值依然考虑拆开,对每个数的 \(a,b\) 分别定正负号,然后分析方案合法性(大部分定号方案合法),再进行调整。
总结:法一是让合法的方案调整到最优,法二是最优的方案调整到合法。
P11882
对众数的颜色进行二进制拆分,把二进制某位为 \(1\) 的全部拎出来做一遍,然后再 check 求出来的数是不是众数。
P9288
扫描线加 KTT 模板。但是从 KTT 双侧递归,满足条件就弹掉,还能分析出正确复杂度来看(同时结合吉司机线段树,以及一些这样的乱搞正解过题的例子),写这样的线段树结构收益很高!!!多想点剪枝上这样的结构很可能能通过题目。
qoj 4998
区间查相等依然是哈希维护,区间钦定相等依然是连边考察联通块。注意到合并联通块只会合并 \(O(n)\) 次,直接启发式合并转成合并 \(O(n\log n)\) 个元素。
然后只需要快速找出合并点,二分哈希即可。
交流总结
-
点分治不只能处理链的性质,也能处理联通块的性质。比如说强制分治中心出现/不出现在联通块中,然后递归子树。
-
dp 优化:状态数太多可以考虑合并若干相同值的状态,或者合并若干转移方式相同的状态。
-
dp:合法方案有时候也要考虑容斥,特别是当不合法能带来很多性质(比如推其他位置合法)的时候。
-
在 可重状态如何计数 的基础上,计数 dp 还有一个很大的方法就是拆贡献!
-
对联通块计数:要么考虑点减边容斥(更进一步的是平面图欧拉定理),要么考虑联通块取代表元计数。
-
小 trick:考虑 \(p\) 是一颗树的 bfs 序,若 \(p_u<p_v<p_w\),则 \(\text{dis}(u,v)\le \max(\text{dis}(u,w),\text{dis}(v,w))\)。
\(\boldsymbol{[2025/06/05]}\)
gym102586J
DFA-dp 例题,如果建立出 DFA 以及转移就能快速 dp。
给一个我不会证明的方法。 首先判断(猜测)出状态数不多。 记 \(\text{check}(s) = 0/1\) 表示 \(s\) 是否能缩成 \(1\)。 如果两个串 \(s_1, s_2\) 是等价的, 如果他们后面同时接任何一个串 \(t\), 一定有 \(\text{check}(s_1+t) = \text{check}(s_2+t)\)。 实际操作中, 对长度不超过 \(10\) 的所有 \(t\) 都判断一下就可以了。
对于具体实现,就用一个 int 存 \(01\) 串,从低位到高位表示这个串从前到后的字符,最高位人为补充了一个 \(1\) 表示结束(这是为了方便判断串的长度)。搜索时每次往最低位增加一个字符,所以读入的字符串时要先翻转。
染色
\(\boldsymbol{[2025/06/07]}\)
gym104819F
K4 及其衍生物的容斥计数。K4 计数。
极好的 Jerry's blog!
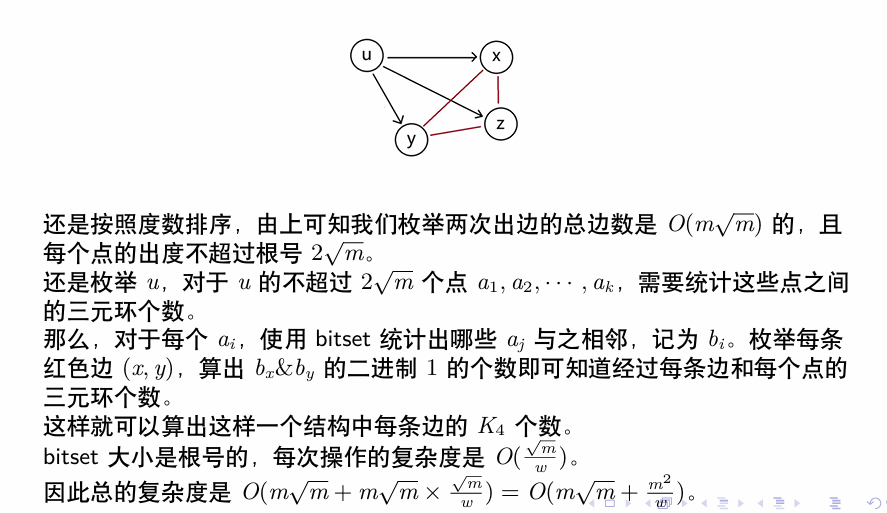
然后就是记下每条边都在几个 K3,K4 里,扣掉算重的东西即可。
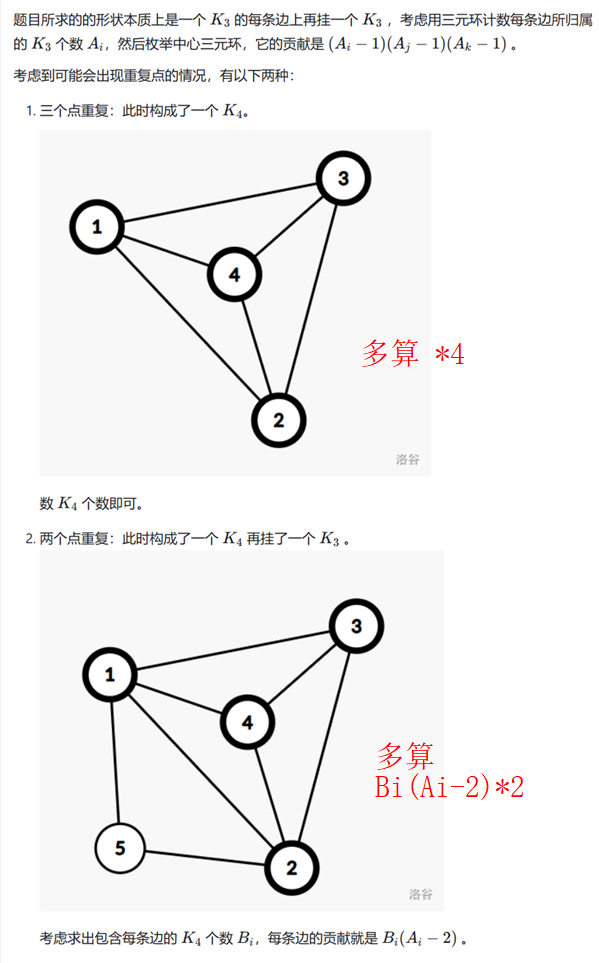
交流总结
-
分阶段贪心:qoj 9424。具体的,分一个障碍阻挡 \(2,1,0\) 对车去贪心。
-
答案可能的值域比较小带来的优化,有时甚至转成判定性问题,在 05/29 交流总结中也有提到。
-
一类猜结论:先去掉一些很烦的条件找到明显结论,然后加上条件,做调整法,使得调整的量不大。
-
dp 转移 \(f_A\times f_B\to f_C\) 的时候应该确认 \(A,B\) 的独立性,如果不独立,可以尝试乘一些系数消贡献。
-
每次消连续段合并左右的区间 DP:例题。考虑 \(f_{l,r}\) 表示区间答案,\(g_{l,r,mx,mn}\) 表示区间删到只剩 \(mx,mn\) 的时候的答案,辅助转移!
转移 \(f\) 用 \(g\),转移 \(g\) 就考虑 \(r+1\) 要么归到 \([l,r]\) 中贡献极值,要么和后面一段连续区间一起取,通过 \(f\) 转移即可。
辅助数组交替转移在 CF1874F 中亦有记载。
\(\boldsymbol{[2025/06/09]}\)
Triomino Tiling
杨表题。
给定 \(n,m\),有一个由 \(n\) 个 \(0\),\(m\) 个 \(1\) 组成的 \(01\) 串,初始 \(0\) 全在前面,最后要变成 \(1\) 全在前。
每次可以选择一个相邻的 \(01\to 10\),求方案数。
方案数为 \(n\times m\) 的矩形杨表个数,记为 \(Y(n,m)\)。
还有个轮廓线 trick 也挺不错。考虑填好的位置和未填好的位置的轮廓线,上看做 \(0\),右看做 \(1\)。
分讨容易发现:每次恰好交换 \(a_i\) 和 \(a_{i+3}\),初始是 \(n\) 个 \(0\),\(m\) 个 \(1\) 依次排列。
于是 \(\bmod 3\) 分成三组,分别做即可。但是注意到还要给三组分配编号,设三组 \(01\) 总个数分别为 \(c_0,c_1,c_2\)。
于是答案为 \(\dfrac{(nm/3)!}{c_0!c_1!c_2!}\prod\limits_{i\in \{0,1,2\}}Y(c_{i,0},c_{i,1})\)。
注意到下面三个阶乘和杨表里的阶乘抵消了。于是计算瓶颈在于 \((nm/3)!\)。
复杂度 \(O(nm/3)\)。
计划要求
每天定好要做的事情(一定不能太多!),由于不好控制具体时间段,于是钦定好先后顺序,使得留空时间能多安排。
\(\boldsymbol{[2025/06/10]}\)
P8204
Top Cluster 树分块模板。界点链是直链!
分成若干簇后,考虑若 \(x\) 不在簇的界点链上,则 \(x\) 的邻域大小显然不超过 \(O(\sqrt n)\),暴力加入即可。
否则对每个簇单独考虑,把询问挂在簇的底界点,然后按照 \(dep_{x}+y\) 排序。每组询问先移动到底界点(由于排序后于是是递增的),然后由这个调整到 \((x,y)\)。
每个簇移动到底界点的代价和显然是 \(O(n)\)(每个点一次),然后对于每个询问调整显然和不在簇链上的情况类似,不超过 \(O(\sqrt n)\)。
\(\boldsymbol{[2025/06/11]}\)
ARC168F
大部分模拟费用流题都会有一条链的流,提供数据结构维护。
交流总结
-
任意括号串的最大深度(找到原串一个合法括号匹配子串,其括号树深度)可以如下求:找到一个位置,使得其左侧左括号个数等于右侧右括号个数,那么这个个数就是最大深度。CF1264D2。
-
多观察答案/dp 数组合法状态的构成若干连续段等结构,快速对这些结构转移。在 06/04 中的交流总结也有记载类似思想。QOJ6355. 5,ARC125F。
-
中位数,\(a_i\gets \max(a_j,a_k)\) 等题目可以考虑按照 \(\le x,>x\) 划分 \(01\)。对于求最长/最短时间达成某个状态类型,答案一般就是每个 \(x\) 的 \(01\) 串的答案 \(\min/\max\) 起来。CF1322E Median Mountain Range,P11845。
\(\boldsymbol{[2025/06/12]}\)
ARC160E
需要抓到一些关键点分析,比如这题的叶子。
gym103428C
依然是精准覆盖思想,对于朴素 dp 转移,二分哈希 LCP 找到第一个需要转移的位置,转移过去即可。复杂度两只 \(\log\)。
但是这个题同样引出了一个经典乱搞,就是如果求出所有可能答案后直接 break。这题我们通过裴蜀定理,可以把可能答案定义为所有数和 \(p-1\) 的 \(\gcd\)。然后 bitset 优化 dp 即可。
完全无法卡掉。
qoj 4299
肯定是流子建模。这题观察到二分图建模会比较好,钦定某些点在第一个,某些在第二个,形成了 \((a_1, b_1), (a_2, b_2), \dots, (a_m, b_m)\) 的序列。
只需要知道 \(i\) 在第一个的序列 \(\{b_i\}\),就可以最小费用最大流求解。
由于欧拉回路经典结论有 \(b_i\in\{\lfloor \frac{a_i}{2} \rfloor, \lceil \frac{a_i}{2} \rceil\}\),于是枚举即可。
交流总结
\(\boldsymbol{[2025/06/15]}\)
ARC149D
也是缩等价状态的思想,注意到相反数关系会一直保持,值域不大,直接暴力合并等价类即可。
Multum in Parvo
CF1264D2
括号序列的深度可以如下刻画:枚举分界点,使得其左侧 ( 等于右侧 ),此时这个个数就是深度。
\(\boldsymbol{[2025/06/17]}\)
P12827
区间选偶数个数异或:相当于你 \(a'_{i}\gets a_{i}\bigoplus a_{i+1}\),然后条件等价于 \([l,r-1]\) 中选任意数异或。
同理:选奇数个数我们直接强制钦定选 \(a_l\),然后再在 \(a'\) 的 \([l,r-1]\) 中选任意数异或即可。
有另一个很巧妙的思想:由于都是要求值不超过某个数,你可以给所有数的最高位更高的地方都填上 \(1\),这样必须选偶数个数才能达到不超过的条件。
奇数和上面同理,钦定 \(a_l\) 必选。
然后异或最大值是好求的,\(\le x\) 方案数那个考虑单侧递归,本来是 \(2^{\text{线性基大小}}\) 的枚举,但是注意到每层只有一个有效值(二进制前缀与 \(x\) 相等),否则恒 \(<x\) 或 \(>x\),直接计算答案即可。于是单侧递归,单次复杂度仍然为线性基大小。
这两种做法是等价的。本质上是在干什么呢?是给原来二进制数加上一个 \(01\) 占位符,表示选不选,然后最后偶数奇数就看占位符。
然后异或最大值是好求的,\(\le x\) 方案数那个考虑单侧递归,本来是 \(2^{\text{线性基大小}}\) 的枚举,但是注意到每层只有一个有效值(二进制前缀与 \(x\) 相等),否则恒 \(<x\) 或 \(>x\),直接计算答案即可。于是单侧递归,单次复杂度仍然为线性基大小。
\(\boldsymbol{[2025/06/18]}\)
P12865
冒泡 \(k\) 次后,\([1,r]\) 前缀和的结果为 \([1,\min(r+k,n)]\) 中前 \(r\) 小的和。题解
P11618
注意到除了要给树定拓扑序外,还要排除同构子树的影响,难点在于子树同构判定。同时上个换根 dp 就行了。
qoj 11116
树/图论交互题一个很经典的套路就是递归子问题。把若干联通块之间的边确定好,递归下去联通块。
这题就找到距离最远的链,确定链上所有点,递归挂在上面的子树。每次期望是根号分块,于是次数 \(2n\log\log n\) 左右,可能跑不满。
\(\boldsymbol{[2025/06/19]}\)
P10630
我把这归类为平几维护相对顺序的问题。类似题目 P4864,还有 nfls《直线交点》。
上面两题说的事情是:按 \(x\) 坐标做扫描线,维护直线在 \(x=X\) 时的相对顺序(例如求 \(\texttt{kth}\))。
可以把直线看成序列中的元素,初始按照斜率排序(\(x=-\infty\) 的值)。
然后每扫到一个交点,交换对应两条线在序列中的位置,就维护了相对顺序。
交换次数为 \(O(n^2)\)。
- 这题其实不太一样,是把点投影到直线上,要维护点的相对顺序。
\(\boldsymbol{[2025/06/22]}\)
Maximum Deviation Spanning Tree
Tree I 形 wqs 二分可以分别排序双指针做到 \(1\log\)。
仍然是拆绝对值,分析符号。发现 \(n-1\) 偶的时候中位数没有贡献。
然后你把和中位数差的 \(\sum\) 改成钦定符号的最大值,就可做了。
\(n-1\) 奇数就把最大生成树换成最大生成二树即可。
CF1266H
图上走来走去,\(n,q\) 还这么小,当然是列方程啦!猜一手矩阵可逆,预处理逆,做到单次 \(n^2\) 解方程。
经典 trick:\(x\ge 0\Leftrightarrow x\bmod p_1=x\bmod p_2\),其中 \(\vert x\vert<p_1,p_2\)。
类欧拉路径的东西,一定要判断连通性一类的东西!
\(\boldsymbol{[2025/06/23]}\)
AGC048F
为了好看,rev 一下 \(s\),这样 \(s_{p_k}=1\to s_{p_1}=1\)。
每次就是选一个 \(101010\dots\) 这样的,记为好串。
-
考虑找到一个合法解,发现每次选最长好串删除,此时容易调整证明若有解这个一定是一组解。
-
考虑选 \(10\) 交替这种东西很能调整啊,猜一手:对于一个合法状态(比如上面求的那个),
每步调整 \(\epsilon\) 个 \(01\) 的归属,能遍历所有合法状态。
然后你形式化描述你猜的结论:
设不断贪心取最长取出的长度为 \(l_1\ge l_2\ge \dots\ge l_k\)。
则集合 \(x_1\ge x_2\ge \cdots \ge x_m\) 合法当且仅当:
- \(\sum \lfloor \frac{l_j}{2} \rfloor = \sum \lfloor \frac{x_j}{2} \rfloor,\sum\limits \lceil \frac{l_j}{2} \rceil = \sum \lceil \frac{x_j}{2} \rceil\),即 \(01\) 个数要正确。
- 对于 \(\forall 1 \leq i \leq k\),有 \(\sum\limits_{j \leq i} \lfloor \frac{l_j}{2} \rfloor \geq \sum\limits_{j \leq i} \lfloor \frac{x_j}{2} \rfloor\),限制 \(0\) 的个数。
- 对于 \(\forall 1 \leq i \leq k\),有 \(\sum\limits_{j \leq i} \lceil \frac{l_j}{2} \rceil \geq \sum_{j \leq i}\limits \lceil \frac{x_j}{2} \rceil\),限制 \(1\) 的个数。
然后随便 dp 即可。
CF1667E
重心的三种求法(本题使用第三种):
-
最大子树最小的点。
-
所有子树大小都 \(\le \left\lceil\dfrac{n}{2}\right\rceil\)。
-
深度最深的 \(sz\ge \left\lceil\dfrac{n}{2}\right\rceil\) 的点。
\(\boldsymbol{[2025/06/24]}\)
P10873
从一个简化的问题的开始,如果想让猜对自已帽子颜色的人总数不少于 \(\lfloor N/2 \rfloor\) 怎么做。
考虑帽子为红色的人的集合 \(S\),对于某个人 \(i\),设 \(i \notin S\),他在所有人的状态为 \(S\text{ \color{red}or }S + \{i\}\) 中只能猜对一个。
因此我们可以将 \(S\) 和 \(S + \{i\}\) 连一条边,并对整张图定向,如果最终图中的边是 \(S \to S + \{i\}\),就在当前状态下猜测帽子颜色为白,否则猜测红。
但这题要对红白分别限制,考虑拆点,连边 \((S, 0), (S + \{i\}, 1)\) 即可。分别表示 \(S\) 状态下红/白的限制。
P11973
问题转化为:环上 \(n\) 白点 \(n\) 黑点,可能重合,两点匹配权值为环上最小距离,求最小权完美匹配。
这东西有个经典 trick:拆贡献到边。就是对每条边算对距离的贡献,而不是直接绝对值。P3992 中也要用到。
初始直接把黑白点从编号 \(1\) 开始拍到序列上,黑点 \(x\) 让 \(c_x\gets c_x+1\),白点则 \(c_x\gets c_x-1\)。
然后对 \(c\) 前缀和,此时从 \(1\) 开始的答案就是 \(\sum\limits_{i=1}^{2n} \vert c_i\vert\)。
-
循环左位移 \(1\) 次,前缀和数组变成:\([c_2-c_1,\cdots,c_n-c_1,0]\)。
-
循环左位移 \(2\) 次,前缀和数组变成:\([c_3-c_2,\cdots,c_n-c_2,c_1-c_2,0]\)。
-
以此类推,循环位移 \(k\) 次后,答案变成:\(\sum\limits_{i=1}^{2n} \vert c_i-c_k\vert\)。
这东西最小值是啥?显然取中位数,做完啦!
于是求解复杂度 \({\mathcal {O}}(n\log n)\),瓶颈在于排序。
\(\boldsymbol{[2025/06/25]}\)
P11394
这一类 Boruvka 题目的特征就是单点 bfs 判断可达性很好做,但是被可达性(反向可达)不好做。
最终求可达点最少的点是哪些。
简单点说,就是求缩点后 DAG 里 \(\text{out}=0\) 的点对应的 SCC 中的所有点,然后再找一次最小就求出答案了。
- 换句话说,就是求 DAG 叶向树的叶子,所以 Boruvka 终归还是跳出不了和生成树的联系。
这类问题我们如果要求出每个点可达多少点,一般是不弱与 DAG 可达性的,不太能做。
于是要充分利用性质。
一开始把每个点染不同的颜色,下面把同颜色的点称作一个连通块。
并查集维护若干连通块,连通块只保留一个所有点能到它的点(代码中写作并查集的根),也就是连通块中能到达的点数量最少的点。(其他的点不用管,因为只要求达到点数最小的)
然后每次从保留的点开始 bfs 找。设当前从 \(x\) 开始 bfs:
-
若走到不同连通块的点,就合并两个连通块并返回,\(x\) 点就可以直接废了,保留不同那个。
-
若不能走到不同连通块,就说明 \(x\) 能到的位置已经确定。
\(y\) 和 \(x\) 在同一个 SCC 的充要条件是 \(y\to x,x\to y\)。
前者代表 \(y\) 在 \(x\) 的并查集里,后者代表 \(x\) 出发能走到 \(y\)。
于是就能找出 \(x\) 所在的整个 SCC,以后可以不再 bfs 这个连通块,丢掉然后更新答案即可。
每轮每个连通块要么和其他合并,要么被丢掉,通块数量至少 \(/2\)。
这样只会经过 \(\log\) 轮 bfs,复杂度为 \({\mathcal O}(m\log n)\)。
CF1305G
Boruvka 做生成树还是比较经典的,不那么板的例题有:AT_cf17_final_j,P6199 等等。
优势在于把 MST 问题 \(\times \log\) 转化为给每个点赋颜色,对每个点求不同色的最小/大距离。
然后就是高维前缀信息合并板子题。
P12558
首先将 \(a,b\) 按照从小到大排序。
依然先考虑判定性问题,如何判定 \(S\) 是否可行?
我们当然是直接贪心匹配,比如:最小的 \(S\) 内的 \(a\) 必须匹配最小的 \(b\),最大的 \(T\) 内的 \(b\) 必须匹配最大的 \(a\)。
记 \(T = \{1, 2, \dots, n\} \setminus S\),易知 \(S\) 合法的充要条件是:
- \(a_{S_i} > b_i\)
- \(a_{T_i} < b_{|S|+i}\)
此时我们可以枚举 \(|S|=m\),然后 \(f_{i,j}\) 表示考虑前 \(i\) 个 \(a\),有 \(j\) 个在集合 \(S\) 的方案数,时间复杂度 \(\mathcal{O}(n^3)\)。
考虑优化,你发现每次 dp 的形式很类似,你每次重新做一遍很唐。
我们按照 \(b_{|S|}\) 把序列 \(a\) 划分成两个部分 \(a_1\sim a_k\) 和 \(a_{k+1}\sim a_n\),其中 \(k\) 满足 \(a_k < b_{|S|} < a_{k+1}\)。
我们发现 \(a_1\sim a_k\) 天然能放进 \(T\),\(a_{k+1}\sim a_n\) 天然能放进 \(S\)。
于是你只要考虑前缀是否放进 \(S\),后缀是否放进 \(T\)。
我们只需要对前后缀分别做一个背包然后卷起来即可,这东西和 \(|S|\) 无关!就把前后缀独立开来了。
比如后缀记 \(g_{i,j}\) 表示 \([i,n]\) 选了 \(j\) 个进 \(S\) 的方案数。如下转移:
- \(g_{i,j+1}\gets g_{i+1,j}\)
- \(g_{i,j}\gets g_{i+1,j}(a_i<b_{i+j})\)
时间复杂度 \(\mathcal{O}(n^2)\)。这题还是一个拆条件独立的思想。代码很简单。
\(\boldsymbol{[2025/06/26]}\)
CF1608F
记 \(M_i=\text{mex}(a_1,a_2,\cdots ,a_i)\)。
\(\text{mex}\) 变化的难点在于:移动一次 \(i-1\to i\) 之后若 \(a_i=M_{i-1},M\) 值要增大,
则 \([1,i)\) 内的数可能继续使 \(M\) 增大,你不好记录 \([1,i)\) 中每个点的信息。
这时候最牛的一步来了:注意到 \([1,i]\) 中 \(\le M_i\) 的值肯定没用了,而 \(>M_i\) 的值我们只关心其不同数的个数!
于是就能列 dp 了:\(f_{i,j,k}\) 表示考虑了 \(1\sim i,M_i=j\),\([1,i]\) 中有 \(k\) 种不同的 \(>j\) 的数的方案数。
然后上前缀和优化即可,做到 \(O(n^2k)\)。
\(\boldsymbol{[2025/06/27]}\)
qoj 10306
顺推做法算是在做 ddp 状物,只是要探究很多性质。
猜结论做法的反推很自然,但是正推比较不自然。只能说我见过好几个调整法调整前缀的题了,可以积累思路。
最后 dp 的转移优化大概还是:相同的转移合并一起做,减少重复。
\(\boldsymbol{[2025/06/28]}\)
CF1616G
CF1764H
和 uoj #890. 【UNR #8】兵棋 一样,就是以一定操作删除,问删除后状态的题,变为刻画每个位置被删除的时间,然后这些时间 \(t_i\) 之间有相互转移的性质。
\(\boldsymbol{[2025/06/29]}\)
P8859
钦定最大值在最后,不断循环位移观察性质,然后搞出笛卡尔树,对其形态 dp。
\(\boldsymbol{[2025/06/30]}\)
AGC050F
考虑对消,转化成拓扑序计数。
P11880
-
先钦定都选区间,再看哪些选区间补。
-
二分 \(mid\),枚举 \(k\) 个选区间补,能 \(O(n^2\log ^2 n)\)。
-
都选区间的时候,令 \(V=\max(A_i)\)。注意到 \(k\in[V-mid,V-mid+1]\),枚举计算即可,复杂度 \(O(n\log ^2 n)\)。
\(\boldsymbol{[2025/07/11]}\)
uoj 984
上上下下的 trick,比如 \(x\leftrightarrow y\) 代价为 \(|x-y|\) 类型的题,可以考虑所有权值排序,然后对所有权值分层。
从小到大和前一个不同色就同层,同黑色就下移,白色就上移动。
这样同层黑白交替,并且只需要考虑同层相邻匹配。
在 P2748 中亦有记载。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号