二分图边染色，正则二分图匹配

记号规定：图点数为 $n$，边数为 $m$，图最大点度数为 $D$。本文中探讨的图大多为二分图。

二分图边染色

题意

给你一个无向的二分图。现在将它的每条边染色，使得任意两条相邻（有公共顶点）的边颜色不同。请你计算一种染色方案，使得用到的颜色数量最少。

模板：CF600F

解法

Kőnig 定理：对于无向二分图，其边染色的最小颜色数（即色数）等于图的最大度数 $D$。下面给出做法（构造性证明）：

依次加入 $m$ 条边，对于任意一条边 $(u, v)$，设集合为点 $u$ 连边的颜色集为 $C_1$，点 $v$ 连边的颜色集为 $C_2$。

定义 $\text{mex}(S)$ 为不属于集合 $S$ 的最小正整数。令 $x=\text{mex}(C_1),y= \text{mex}(C_2)$。

若 $x=y$：即存在一种颜色使得集合 $C_1$, $C_2$ 中都不包含并且最小。直接用其将 $(u, v)$ 染色。
若 $x \neq y$：说明在集合 $C_2$ 中存在一种颜色等于 $x$。

找出这条边，设为 $(v, u_2)$，这条边的颜色等于 $x$。

将 $(u, v)$ 强制染上 $x$，此时 $(u, v)$ 与 $(v, u_2)$ 颜色冲突。

交换 $v$ 中颜色为 $x,y$ 的两个出点，此时 $(u, v)$ 与 $(v, u_2)$ 颜色不冲突，即 $(v,u_2)$ 的颜色为 $y$。

但是 $(v, u_2)$ 可能与 $(u_2, v_2)$ 颜色冲突，考虑循环使用如上方法解决（即交换颜色为 $x,y$ 的出点），直到不存在冲突。

接下来我们证明：一次这个过程不会走重复顶点。（黑色是加边前的颜色，红色是加边后的，彩色是考虑的重复）

若重复点在 $u$：

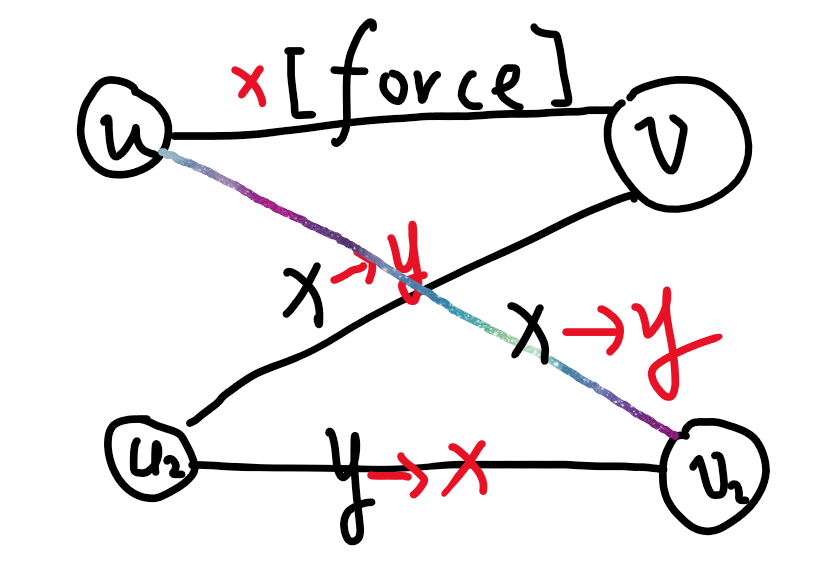
则初始有条颜色为 $x$ 的彩色边，与 $\text{mex}(C_1)=x$ 矛盾。

若重复点在其他点 $u_2$：

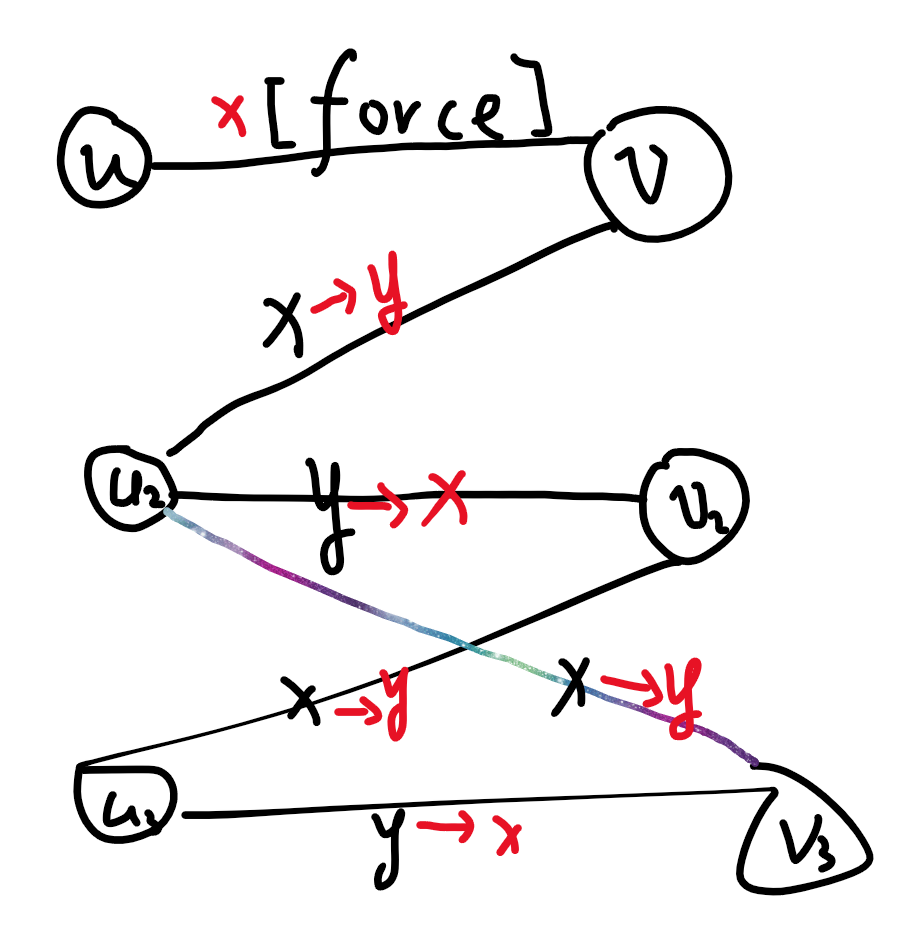
由于在走 $u_2\to v_2$ 改成的 $x$ 是由原来彩边 $u_2\to v_3$ 的 $y$ 交换过来的，于是走彩边 $v_3\to u_2$ 的时候不会再有其他边颜色为 $y$，即 $(u_2,v_2)$ 的 $x\to y$ 和 $(u_2,v_3)$ 的 $y\to x$ 是同步的。

于是我们加 $m$ 条边，每轮加边操作次数不超过点数 $n$，于是复杂度 $O(nm)$。

实际操作次数根本跑/卡不满，常数极小。于是这个算法通用性强，即便是对比一些复杂度更优秀的算法。

$\texttt{code}$

#include<bits/stdc++.h>
#define LL long long
#define P pair<int,int>
#define fi first
#define se second
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
const int N=2005,M=1e5+5;
int n,m,in[N],C,to[N][N];P e[M];
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m>>C;
	for(int i=1,x,y;i<=C;i++) cin>>x>>y,y+=n,in[x]++,in[y]++,e[i]={x,y};
	int ans=*max_element(in+1,in+1+n+m);cout<<ans<<"\n";
	for(int i=1;i<=C;i++)
	{
		auto [u,v]=e[i];int t1=1,t2=1;
		while(to[u][t1]) t1++;
		while(to[v][t2]) t2++;to[u][t1]=v;to[v][t2]=u;
		if(t1==t2) continue;
		for(int c=t2,w=v;w;w=to[w][c],c^=t1^t2) swap(to[w][t1],to[w][t2]);
	}
	for(int i=1;i<=C;i++)
	{
		auto [u,v]=e[i];
		for(int j=1;j<=ans;j++) if(to[u][j]==v){cout<<j<<" ";break;}
	}
	return 0;
}

等价命题

边染色与匹配的关系：在二分图中，边染色问题等价于将边划分为 $D$ 个匹配（即每个匹配中的边两两不相邻）。

正则二分图匹配

题意

给定一个正则二分图 $G=(X,Y,E)$，其中 $|X|=|Y|=n$ 且每个点的度数均为 $k$，请你求出一个其完美匹配。

模板：loj 180

解法

参考资料：_rqy：Hall 定理；正则二分图的完美匹配

值得注意的是，按照上述方法找一个 $n$ 个点的 $k-$ 正则二分图的完美匹配，复杂度为 $O(nk+n\log n)$。其中 $nk$ 表示边数。

事实上：存在确定性同复杂度的正则二分图的完美匹配算法，但是太难写了被丢了。

大概就是 $k$ 奇数的时候加一些假边，然后一直做，最有一直缩减假边数目直到没有。（我也不是很会，也有可能会多一只 $\log$）

$\texttt{code}$

#include<bits/stdc++.h>
#define LL long long
#define fr(y) freopen(#y".in","r",stdin);freopen(#y".out","w",stdout);
using namespace std;
const int N=4e6+5;
mt19937 rnd(time(0));
int n,d,w[N],p[N],t,a[N];
vector<int>E[N];bool v[N];
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>d;
	for(int i=1,x;i<=n;i++)
	{
		E[i].resize(d);p[i]=i;
		for(int j=0;j<d;j++) cin>>x,E[i][j]=x+n;
	}shuffle(p+1,p+1+n,rnd);
	for(int I=1;I<=n;I++)
	{
		int x=p[I];
		while(x)
		{
			v[a[++t]=x]=1;x=E[x][rnd()%d];
			while(v[x]) v[a[t--]]=0;
			v[a[++t]=x]=1;x=w[x];
		}
		while(t)
		{
			int x=a[t--],y=a[t--];
			w[x]=y,w[y]=x;v[x]=v[y]=0;
		}
	}
	for(int i=1;i<=n;i++) cout<<w[i]-n<<" ";
	return 0;
}

求出一个 $k$ 组匹配的方案

但是如果要求出一个 $k$ 组匹配的方案呢？我们直接做 $k$ 次，是 $O(nk^2+nk\log n)$ 的，足够应付大多数题目。

但是我们也可以分治，如果 $k$ 是奇数就找一组匹配递归下去。否则由于每个点度数均为偶数，我们找出一组欧拉回路并定向，均匀分成两半。这样就变成了两个 $k/2-$ 正则二分图的问题。

于是复杂度 $O(nk\log k+nk\log n)$。这个基本是目前最优复杂度了。

为什么边数的 $nk$ 一定要算进复杂度内呢？

因为每次删完一次匹配后你要更新所有边看是否被删，直接 set 删也不好做中间的其他过程。

而找一个 $n$ 个点的 $k-$ 正则二分图的完美匹配非读入的复杂度是 $O(n\log n)$ 的。

例题：qoj 10045

两者关联与论文探究

边染色与匹配的关系：在二分图中，边染色问题等价于将边划分为 $D$ 个匹配（即每个匹配中的边两两不相邻）。

于是边染色问题能通过这个算法做到 $O(nD(\log n+\log D))$！即补全为 $D-$ 正则图。

对于正则二分图匹配，直接暴力边染色做理论最坏复杂度是 $O(nk(n+k))$ 的，并且能求出 $k$ 组完美匹配。但是把边的顺序随机一下能跑挺快，尤其是 $n$ 很大的时候。

$n$ 很小的时候可以拼一些暴力找单组匹配，也能做到实际效率很优秀。

模板题直接上能 $75$：$\bf{submission}$

附一点困难论文：

例题

最后给一道例题：拉丁方

题解

首先考虑 $R = n$ 时怎么做，此时我们可以确定所有行剩余部分可以填的数的集合，我们只需保证每一列的数不重复就够了。

我们将每一行作为左部点，每种数作为右部点，如果该行可以填某个数则连一条边，这是一张二分图，且每个点的度数均为 $n - C$。

根据上面的讨论，我们需要将其划分成 $n - C$ 组完美匹配，每一组匹配确定了每一列填哪些数。

我们知道，一张二分图的边染色数是它每个点度数的最大值。因此我们可以求出这张图的一个 $n - C$ 边染色，对于每种颜色的所有边，易知它们构成了一组完美匹配。

只需要利用 CF600F 的方法求一次二分图边染色即可，时间复杂度 $O(n^3)$。

再考虑 $R \neq n$ 的情况。我们考虑先填左下角的部分，将问题转化为 $R = n$ 的情况。

同样可以确定前 $C$ 列可填的数的集合，利用同样的方式建图，我们得到了一张左部点度数均为 $n - R$ 的二分图。

如果某个右部点的度数大于 $n - R$，这意味着某个数出现的次数超过 $n - R$，但是未填的 $n - R$ 行中，每行至多填一个，因此此时必然无解。

所以该二分图有 $n - R$ 边染色，每种颜色的边对应一组左部满的匹配，对应每一行所填的数的集合。

只需再跑一次二分图边染色即可，时间复杂度 $O(n^3)$。

瓶颈在于求出一个 $k$ 组匹配的方案，选一个你自己愿意写的算法即可。

$\texttt{code}$

#include<bits/stdc++.h>
#define LL long long
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
const int N=505;
int T,n,A,B,a[N][N],c[N<<1][N],b[N];bool v[N];
inline void cl(int n,int d){for(int i=1;i<=n;i++) fill_n(c[i]+1,d,0);}
inline void add(int u,int v)
{
	int x=1,y=1;
	while(c[u][x]) x++;while(c[v][y]) y++;
	c[u][x]=v,c[v][y]=u;
	if(x==y) return;int z=x^y;
	for(int w=v,C=y;w;w=c[w][C],C^=z) swap(c[w][x],c[w][y]);
}
inline bool sol1()
{
	fill_n(b+1,n,A+B);
	for(int i=1;i<=A;i++) for(int j=1;j<=B;j++) b[a[i][j]]--;
	for(int i=1;i<=n;i++) if(b[i]>n) return 0;
	cl(n+A,n-B);
	for(int i=1;i<=A;i++)
	{
		fill_n(v+1,n,0);
		for(int j=1;j<=B;j++) v[a[i][j]]=1;
		for(int j=1;j<=n;j++) if(!v[j]) add(i,j+A);
	}
	for(int i=1;i<=A;i++) for(int j=1;j<=n-B;j++)
		a[i][j+B]=c[i][j]-A;
	return 1;
}
inline void sol()
{
	cl(n<<1,n-A);
	for(int i=1;i<=n;i++)
	{
		fill_n(v+1,n,0);
		for(int j=1;j<=A;j++) v[a[j][i]]=1;
		for(int j=1;j<=n;j++) if(!v[j]) add(i,j+n);
	}
	for(int i=1;i<=n;i++) for(int j=1;j<=n-A;j++)
		a[j+A][i]=c[i][j]-n;
}
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>T;
	while(T--)
	{
		cin>>n>>A>>B;
		for(int i=1;i<=A;i++) for(int j=1;j<=B;j++) cin>>a[i][j];
		if(B<n&&!sol1()){cout<<"No\n";continue;}
		sol();cout<<"Yes\n";
		for(int i=1;i<=n;i++,cout<<"\n") for(int j=1;j<=n;j++) cout<<a[i][j]<<" ";
	}
	return 0;
}

附：一般图色数

给你一个图。现在将它的每条边染色，使得任意两条相邻（有公共顶点）的边颜色不同。请你计算一种染色方案，使得用到的颜色数量最少。

即第一个问题二分图 $\to$ 一般图。

Vizing 定理：一般图边色数是最大度数 $+0$ 或 $+1$。并且计算一般图准确值是 NPC 的。

posted @ 2025-05-25 09:49 HaHeHyt 阅读(505) 评论(0) 收藏举报

刷新页面返回顶部

Loading

HaHeHyt's blog

二分图边染色，正则二分图匹配