解析几何笔记（2D）

记号约定：

• \(\displaystyle {x \brack y}\)：向量 \((x, y)\)。
• \(\langle \mathbf{u}, \mathbf{v} \rangle\)：向量 \(\mathbf{u}\) 和 \(\mathbf{v}\) 的夹角。
• \(\square\)：证毕。
• \(\operatorname{dist}(a, b)\)：\(a\) 与 \(b\) 的直线距离。

1. 直线

一些定义：

• 方向向量：与直线 \(l\) 平行的向量。
• 倾斜角：直线 \(l\) 与 \(y\) 轴正方向同向的方向向量，与 \(x\) 轴正方向的夹角。
  • 形式化的，设直线 \(l\) 的方向向量 \(\mathbf{v}\) 满足 \(\displaystyle \mathbf{v} \cdot {0 \brack 1} \ge 0\)，则 \(l\) 的倾斜角为 \(\mathbf{v}\) 与 \(\displaystyle {1 \brack 0}\) 的夹角。

一些约定：

• 直线 \(l_1\) 和 \(l_2\) 重合也算做 \(l_1 \parallel l_2\)。

1.1 表示方法

1.1.1 斜截式

可以用 \(l : y = kx + b\) 表示一个直线，其中 \(k\) 为该直线的斜率，\(b\) 为截距。

容易发现，这种形式不能表示形如 \(x = c\) 的直线，因为此时没有对应的 \(k\)。

考虑 \(k\) 的几何意义。我们发现，当 \(x\) 增大 \(h\) 时，\(y\) 增大 \(kh\)。设 \(l\) 的倾斜角为 \(\theta\)，画图可得 \(k = \tan(\theta)\)。

1.1.2 点斜式

如果已知 \(l\) 的斜率 \(k\)，和 \(l\) 上一点 \((x_0, y_0)\)，则 \(l : y = kx + (y_0 - kx_0)\)。

移项得 \(y - y_0 = k(x - x_0)\)。不要写成 \(\dfrac{y - y_0}{x - x_0} = k\)，因为这样会缩小定义域。

容易发现，这种形式不能表示形如 \(x = c\) 的直线，因为此时没有对应的 \(k\)。其实所有用到斜率的表示方法都有这个问题。

1.1.3 两点式

如果已知 \(l\) 上两点 \((x_1, y_1) \neq (x_2, y_2)\)，则 \(l : (x_2 - x_1)(y - y_1) = (y_2 - y_1)(x - x_1)\)。

其实就是 \((x, y)\) 与 \((x_1, y_1)\) 的斜率和 \((x_2, y_2)\) 与 \((x_1, y_1)\) 的斜率相等。或着也可以想成 \(\displaystyle {x - x_1 \brack y - y_1} = \lambda {x_2 - x_1 \brack y_2 - y_1}\)。

有一个特例，如果已知 \(l\) 上两点 \((0, y_0), (x_0, 0)\)，则 \(l : x_0 y + y_0 x - x_0 y_0 = 0\)。

1.1.4 一般式

这玩意儿用处不大。

可以用 \(ax + by + c = 0\) 描述一个直线（\(a, b\) 不同时为 \(0\)），容易发现该直线的斜率为 \(-\dfrac{a}{b}\)。

因为 \(x\) 增加 \(b\) 会让 \(y\) 增加 \(-a\)，所以这个直线的方向向量为 \(\displaystyle {b \brack -a}\) 或 \(\displaystyle {-b \brack a}\)。

那么这个直线的法向量为 \(\displaystyle {a \brack b}\) 或 \(\displaystyle {-a \brack -b}\)。方法也很简单，把 \(y\) 坐标取相反数后，再和 \(x\) 坐标交换。

证明：复数 \(z\) 逆时针旋转 \(90 \degree\) 后为 \(z {\rm i}\)。

则 \(a + b {\rm i}\) 逆时针旋转 \(90 \degree\) 后为 \((a + b {\rm i}) {\rm i} = -b + a {\rm i}\)。

则 \(\displaystyle {a \brack b}\) 逆时针旋转 \(90 \degree\) 后为 \(\displaystyle {-b \brack a}\)。\(\square\)

1.1.5 参数式

如果已知 \(l\) 的倾斜角 \(\theta\) 与 \(l\) 上一点 \((x_0, y_0)\)，则：

\[l : \begin{cases} x = x_0 + t \cos(\theta) \\ y = y_0 + t \sin(\theta) \end{cases} \]

注：在这个式子中把 \(t\) 和 \(\theta\) 交换，就可以得到圆的参数式。直线的是固定角度，圆的是固定长度。

1.2 位置关系

设 \(l_1 : a_1 x + b_1 y + c_1 = 0\)，\(l_2 : a_2 x + b_2 y + c_2 = 0\)。

垂直关系

注意到，\(l_1 \perp l_2\) 等价于它们的法向量垂直，即 \(\displaystyle {a_1 \brack b_1} \cdot {a_2 \brack b_2} = 0\)，即 \(a_1 a_2 + b_1 b_2 = 0\)。移项可得 \(\left( -\dfrac{a_1}{b_1} \right) \left( -\dfrac{a_2}{b_2} \right) = -1\)，即 \(k_{l_1} k_{l_2} = -1\)。

平行关系

然后是平行。我们照葫芦画瓢，把 \(l_1 \parallel l_2\) 转换成它们的法向量平行。发现这样并不好做，因为没有简单的确定的条件。

既然几何法走不通，那就考虑代数法。注意到，\(l_1 \parallel l_2\) 等价于方程组 \(a_1 x + b_1 y + c_1 = 0, a_2 x + b_2 y + c_2 = 0\) 无解或有无穷组解。容易发现，充要条件为 \(a_1 b_2 = a_2 b_1\)。

移项得 \(a_1 b_2 - a_2 b_1 = 0\)，这个形式好熟悉啊。于是我们可以感知出几何法所需要的“简单的确定的条件”：两个法向量围成的三角形面积为 \(0\)，即 \(\displaystyle {a_1 \brack b_1} \times {a_2 \brack b_2} = 0\)，即 \(a_1 b_2 - a_2 b_1 = 0\)。

所以说，共线可以考虑三角形的面积 \(= 0\)，垂直可以考虑两向量点乘 \(= 0\)。

一般关系 I

先搞清楚一般在哪？观察前面两个特例，我们发现夹角在改变，所以这里我们探究 \(l_1, l_2\) 的夹角 \(\theta\) 与 \(l_1, l_2\) 的关系。这里令 \(\theta \in [0, \pi / 2]\)。

接着用法向量。我们发现，如果选择 \(l_1, l_2\) 合适的法向量 \(\mathbf{u}, \mathbf{v}\)，则 \(\mathbf{u}, \mathbf{v}\) 的夹角 \(= \theta\)。

由于我们也不知道什么向量合适，所以先令 \(\displaystyle \mathbf{u} = {a_1 \brack b_1}, \mathbf{v} = {a_2 \brack b_2}\)。此时：

\[\cos \langle \mathbf{u}, \mathbf{v} \rangle = \dfrac{\mathbf{u} \cdot \mathbf{v}}{|\mathbf{u}| |\mathbf{v}|} = \dfrac{a_1 a_2 + b_1 b_2}{\sqrt{(a_1^2 + b_1^2)(a_2^2 + b_2^2)}} \]

接下来调整一下结果。因为 \(\cos(\pi - x) = -\cos(x)\)，所以：

\[\cos(\theta) = \lvert \cos \langle \mathbf{u}, \mathbf{v} \rangle \rvert = \dfrac{|a_1 a_2 + b_1 b_2|}{\sqrt{(a_1^2 + b_1^2)(a_2^2 + b_2^2)}} \]

一般关系 II

用斜截式同样可以描述夹角与直线的关系，而且更简单直接。

设 \(l_1 : y = k_1 x + b_1\)，\(l_2 : y = k_2 x + b_2\)。设它们的倾斜角分别为 \(\theta_1, \theta_2\) 满足 \(\theta_1 \ge \theta_2\)，则夹角为 \(\theta = \theta_1 - \theta_2\)。

因为我们知道 \(\tan(\theta_1) = k_1, \tan(\theta_2) = k_2\)，所以：

\[\tan(\theta) = \tan(\theta_1 - \theta_2) = \dfrac{\tan(\theta_1) - \tan(\theta_2)}{1 + \tan(\theta_1) \tan(\theta_2)} = \dfrac{k_1 - k_2}{1 + k_1 k_2} \]

再限制一下 \(\theta\) 的范围，令 \(\theta \in [0, \pi / 2]\)，则 \(\tan(\theta) = \dfrac{k_1 - k_2}{|1 + k_1 k_2|}\)。

1.3 数量关系

1.3.1 点与直线

点与直线之间的数量关系也只有距离了。设点 \(A(x_0, y_0)\)，\(l : y = kx + b\)，我们想求 \(A\) 与 \(l\) 的距离 \(d\)。

肯定要做过 \(A\) 的垂线。设 \(l \perp l_{\perp}\) 于 \(B\)，且 \(l_{\perp}\) 过 \(A\)，则 \(l_{\perp} : y = -\dfrac{1}{k} x + \left( y_0 + \dfrac{x_0}{k} \right)\)。那么 \(B = \left( -\dfrac{bk - k y_0 - x_0}{k^2 + 1}, \dfrac{b + k^2 y_0 + k x_0}{k^2 + 1} \right)\)。

那么 \(AB = \sqrt{(x_A - x_B)^2 + (y_A - y_B)^2} = \dfrac{|k x_0 + b - y_0|}{\sqrt{k^2 + 1}}\)。

这个式子在说什么呢？观察这个式子，我们发现了 \(l\) 的表达式 \(kx_0 + b\)，这个式子又减了 \(y_0\)。设 \(f(x) = kx + b\)，则分子的几何意义就是 \(A\) 与 \((x_0, f(x_0))\) 的距离。然后看分母，分母是 \(\sqrt{k^2 + 1}\)。但凡做点用 \(\tan(x)\) 反解 \(\sin(x), \cos(x)\) 的题就可以发现这里像是在乘 \(\sin\) 或 \(\cos\)。

注意到 \(l\) 的倾斜角为 \(A\)。我们按照上述内容画出来图，可以发现分子 \(= AC\)，分母 \(= \dfrac{1}{\sin(\angle ACB)} = \dfrac{1}{\sin(\pi / 2 - A)} = \dfrac{1}{\cos(A)} = \sqrt{k^2 + 1}\)。

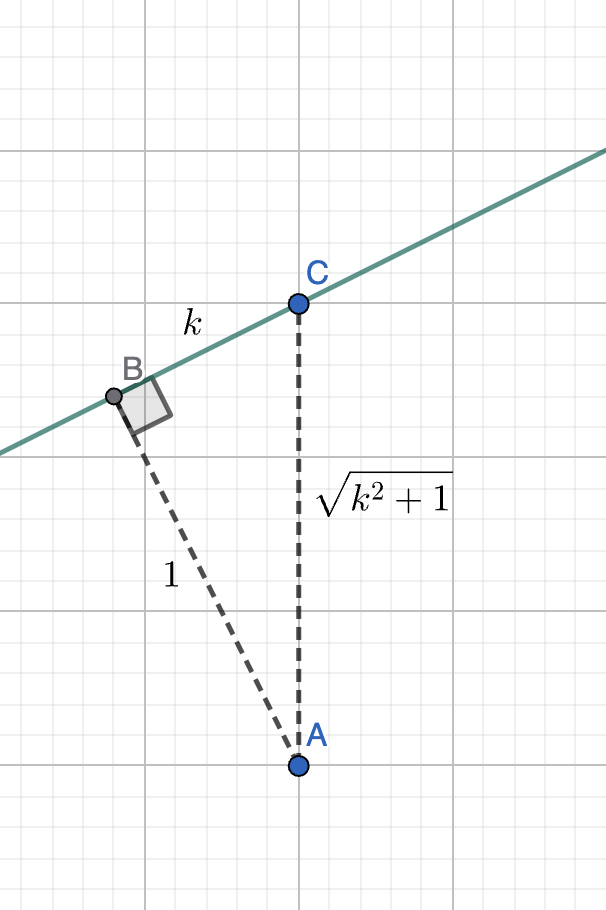
注：图中标的是边的比例，不是长度。

于是 \(AB = AC \cos(A) = \dfrac{|y_0 - f(x_0)|}{\sqrt{k^2 + 1}}\)。

1.3.2 直线与直线

先考虑 \(l_1 \parallel l_2\) 的情况。如果想求 \(l_1, l_2\) 的距离，那么只需在 \(l_1\) 上取一点，然后使用 1.3.1 的公式即可。

再考虑 \(l_1\) 与 \(l_2\) 相交的情况。此时肯定想求交点 \(A(x_0, y_0)\)。设 \(l_1 : a_1 x + b_1 y + c_1 = 0\)，\(l_2 : a_2 x + b_2 y + c_2 = 0\)。把两式联立，然后解方程即可。

2. 圆

2.1 表示方法

2.1.1 标准方程

可以用 \((x - a)^2 + (y - b)^2 = r^2\) 表示一个圆。容易发现，圆心为 \((a, b)\)，半径为 \(r\)。

这个式子实际上就是把距离公式平方得来的。

2.1.2 一般方程

把 \((x - a)^2 + (y - b)^2 = r^2\) 拆开：

\[x^2 - 2ax + a^2 + y^2 - 2by + b^2 = r^2 \]

整理得：

\[x^2 + y^2 - 2ax - 2by + \left( a^2 + b^2 - r^2 \right) = 0 \]

我们设 \(A = -2a, B = -2b, C = a^2 + b^2 - r^2\)，则得到了圆的一般方程：

\[x^2 + y^2 + Ax + By + C = 0 \]

配方得：

\[\left( x + \dfrac{A}{2} \right)^2 + \left( y + \dfrac{B}{2} \right)^2 = \dfrac{A^2 + B^2 - 4C^2}{4} \]

则圆心是 \(\left( -\dfrac{A}{2}, -\dfrac{B}{2} \right)\)，半径是 \(\dfrac{\sqrt{A^2 + B^2 - 4C^2}}{2}\)。容易发现，需要有 \(A^2 + B^2 \ge 4C^2\)。

2.1.3 参数方程

回忆三角函数的定义：\((\cos(\theta), \sin(\theta))\) 表示把 \((1, 0)\) 逆时针旋转 \(\theta\) 后的点。

给坐标乘 \(r\)，可以让这个点与原点的距离为 \(r\)。给两坐标分别加 \(x_0, y_0\)，可以让这个点右移 \(x_0\)，上移 \(y_0\)。

把这两个操作组合起来，就得到了圆的参数方程：

\[\begin{cases} x = x_0 + r \cos(t) \\ y = y_0 + r \sin(t) \end{cases} \]

这个圆的圆心为 \((x_0, y_0)\)，半径为 \(r\)。

2.1.4 三点方程

不共线的三点确定一个圆。我们考虑求点 \(P, Q, R\)（互不共线）确定的 \(\odot O\)。

考虑何时动点 \(S\) 在 \(\odot O\) 上。设 \(\odot O : x^2 + y^2 + Ax + By + C = 0\)，则：

\[\begin{cases} x_P^2 + y_P^2 + Ax_P + By_P + C = 0 \\ x_Q^2 + y_Q^2 + Ax_Q + By_Q + C = 0 \\ x_R^2 + y_R^2 + Ax_R + By_R + C = 0 \\ x_S^2 + y_S^2 + Ax_S + By_S + C = 0 \\ \end{cases} \]

那么可以求出非零的 \(A, B, C\)。

注：此处我们要求 \(\odot O\) 的方程，即 \(A, B, C\)，而不是 \(x_S, y_S\)。

真的可以吗？所以我们关心的实际是这个方程组有没有非零解。

4 个方程，3 个未知数不是很好处理，所以我们加一个未知数 \(D\)：

\[\begin{cases} A(x_P^2 + y_P^2) + Bx_P + Cy_P + D = 0 \\ A(x_Q^2 + y_Q^2) + Bx_Q + Cy_Q + D = 0 \\ A(x_R^2 + y_R^2) + Bx_R + Cy_R + D = 0 \\ A(x_S^2 + y_S^2) + Bx_S + Cy_S + D = 0 \\ \end{cases} \]

首先，\(A = B = C = D = 0\) 一定是解。那么何时有其他解呢？发现限制变强，解的数量一定不会变多，所以要减少限制。如何减少限制？如果有两个方程线性相关，那么可以删去一个，限制就变少了。这时会出现自由元，一定有非零解。有两个方程线性相关，当且仅当：

\[\det \begin{bmatrix} x_P^2 + y_P^2 & x_P & y_P & 1 \\ x_Q^2 + y_Q^2 & x_Q & y_Q & 1 \\ x_R^2 + y_R^2 & x_R & y_R & 1 \\ x_S^2 + y_S^2 & x_S & y_S & 1 \\ \end{bmatrix} = 0 \]

那么：

\[\odot O : \det \begin{bmatrix} x^2 + y^2 & x & y & 1 \\ x_P^2 + y_P^2 & x_P & y_P & 1 \\ x_Q^2 + y_Q^2 & x_Q & y_Q & 1 \\ x_R^2 + y_R^2 & x_R & y_R & 1 \\ \end{bmatrix} = 0 \]

2.1.5 向量方程

这可比 2.1.4 简单多了。

如果已知 \(\odot O\) 的一个直径 \(AB\)，如何求出 \(\odot O\) 呢？注意到，\(P \in \odot O \iff \overrightarrow{AP} \perp \overrightarrow{BP} \iff \overrightarrow{AP} \cdot \overrightarrow{BP} = 0\)。

而 \(\displaystyle \overrightarrow{AP} = {x_P - x_A \brack y_P - y_A}, \overrightarrow{BP} = {x_P - x_B \brack y_P - y_B}\)，那么 \(\overrightarrow{AP} \cdot \overrightarrow{BP} = (x_P - x_A)(x_P - x_B) + (y_P - y_A)(y_P - y_B) = 0\)。

则：

\[\odot O : (x - x_A)(x - x_B) + (y - y_A)(y - y_B) = 0 \]

2.2 阿氏圆

已知 \(A, B\)，动点 \(P\) 满足 \(\dfrac{AP}{BP} = k\)（其中 \(k \neq 1\)），则 \(P\) 的轨迹是圆。

注：\(k = 1\) 时，\(P\) 的轨迹是 \(AB\) 的中垂线，这个显然吧。

先讲一下如何作出这个圆。

注意到这个圆关于 \(AB\) 对称，则 \(AB\) 和圆的直径共线。那么可以在直线 \(AB\) 上找到两个 \(P\) 满足 \(\dfrac{AP}{BP} = k\)。设它们是 \(P_1, P_2\)，则以 \(P_1 P_2\) 为直径作圆即可。

然后我们证明一下这个结论。证明方法千变万化，但是这个应该是最简单的。

证明：如图，设 \(P_1, P_2\) 是上文找到的两个 \(P\)，连接 \(AP, BP, P_1 P, P_2 P\)。

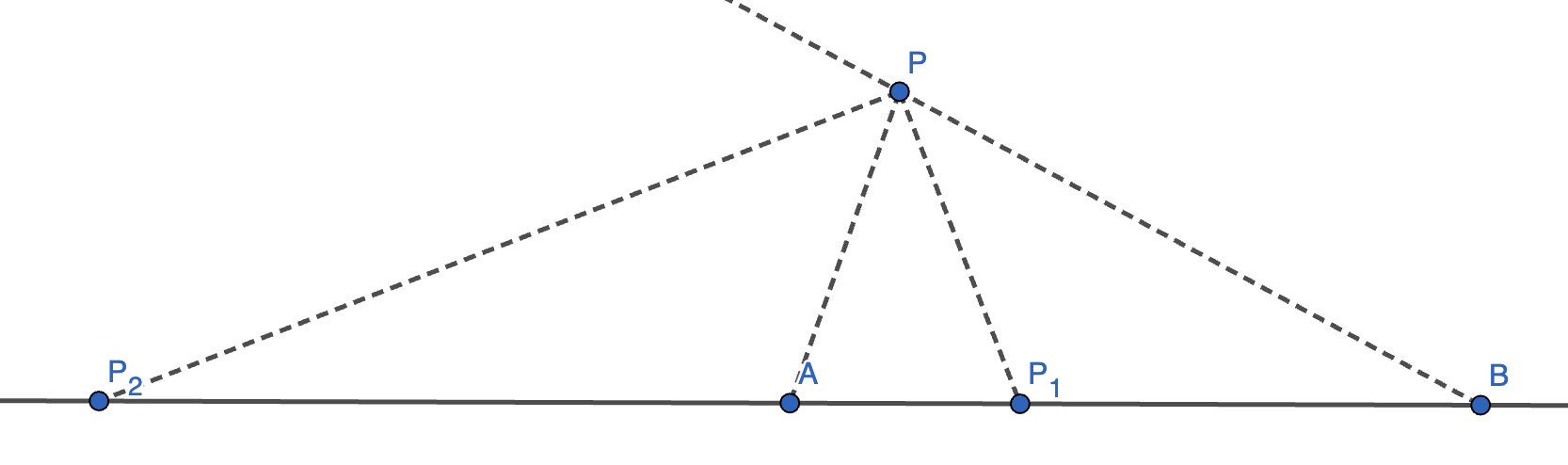
因为 \(\dfrac{AP}{BP} = \dfrac{AP_1}{BP_1} = k\)，所以 \(P_1 P\) 平分 \(\angle APB\)。

因为 \(\dfrac{AP}{BP} = \dfrac{AP_2}{BP_2} = k\)，所以 \(P_2 P\) 平分 \(\angle APB\) 的外角。

所以 \(\angle P_1 P P_2 = 90 \degree\)。

又因为 \(P_1, P_2\) 是定点，所以 \(P\) 在以 \(P_1 P_2\) 为直径的圆上。\(\square\)

那这个圆的方程是什么呢？我们遵循作图的方法，先求出 \(P_1, P_2\)，再求出方程。

\(P_1\) 比较好办，由向量的共线定理，可知 \(P_1 = \left( \dfrac{x_A + kx_B}{k + 1}, \dfrac{y_A + ky_B}{k + 1} \right)\)。\(P_2\) 怎么办呢？用共线定理列方程，可以解出 \(P_2 = \left( \dfrac{x_A - kx_B}{1 - k}, \dfrac{y_A - ky_B}{1 - k} \right)\)。

注：从这里就可以发现 \(k \neq 1\)。

那么代入向量方程，可知圆的方程为：

\[\left( x - \dfrac{x_A + kx_B}{k + 1} \right) \left( x - \dfrac{x_A - kx_B}{1 - k} \right) + \left( y - \dfrac{y_A + ky_B}{k + 1} \right) \left( y - \dfrac{y_A - ky_B}{1 - k} \right) = 0 \]

2.3 反演

2.3.1 对称

我们想作一个点 \(A\) 关于 \(\odot O\) 的对称点，但是这很难定义。

如果我们在 \(\odot O\) 上任选一个点 \(B\)，然后作 \(B\) 关于 \(\odot O\) 的切线 \(l\)，然后定义 \(A\) 关于 \(\odot O\) 的对称点为 \(A\) 关于 \(l\) 的对称点，那就会出问题。这时 \(A\) 关于 \(\odot O\) 的对称点有无穷多个，就倒闭了。

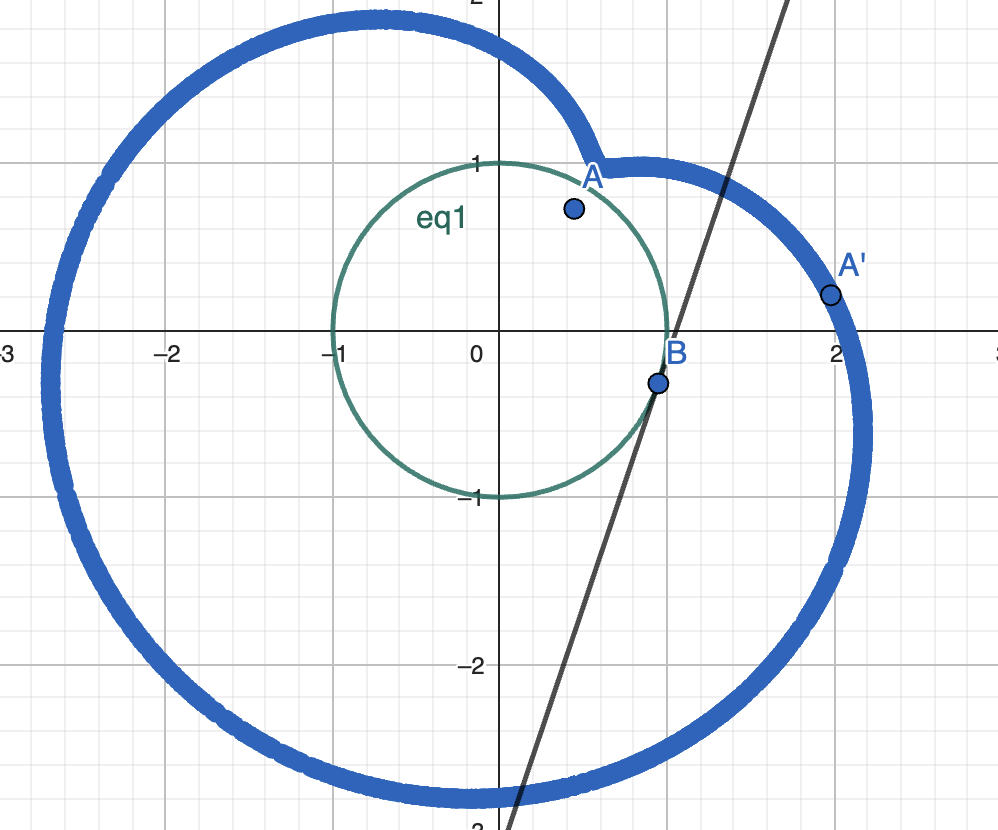
注：你可以按这个定义，把 \(A\) 的所有对称点 \(A'\) 画出来。随着 \(A\) 靠近圆弧，\(A'\) 的轨迹会趋近于一条心形曲线。

于是数学家们想出来了一个比较好的定义。在射线 \(OA\) 上选一点 \(A'\) 满足 \(OA \cdot OA' = r^2\)（\(r\) 为 \(\odot O\) 的半径），定义 \(A\) 关于 \(\odot O\) 的对称点（又叫反演点）为 \(A'\)。容易发现，\(A'\) 是唯一的。

从几何的角度去理解，见下图。其中的“pole”就是对称点。

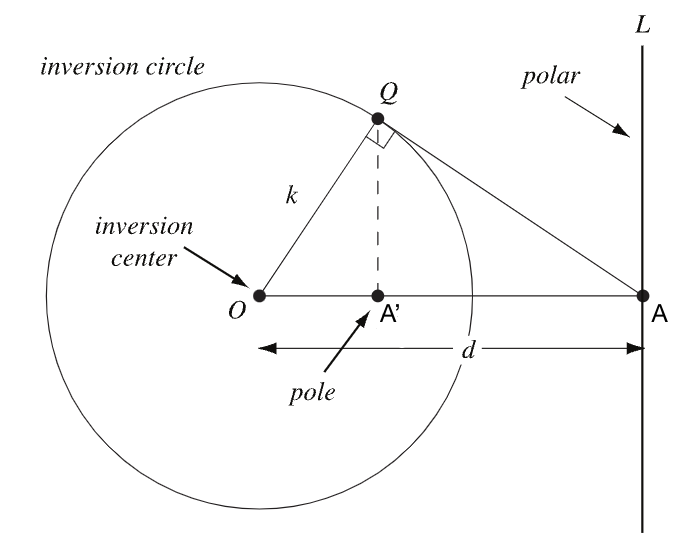
注意到 \(\triangle AQO \sim \triangle QA'O\)，则 \(\dfrac{OQ}{OA'} = \dfrac{OA}{OQ}\)，即 \(OQ^2 = OA \cdot OA'\)。

图中是 \(A\) 在 \(\odot O\) 外面的情况。如果 \(A\) 在 \(\odot O\) 里面，那就交换一下 \(A\) 和 \(A'\) 的标号。这张图顺便给出了尺规作对称点的方法。

接下来就要求一求反演点的坐标了。为了更方便，我们用复数表示点。设圆心为 \(O = 0\)，半径为 \(R\)，我们想求点 \(Z\) 关于 \(\odot O\) 的对称点 \(Z'\)。

我们知道 \(|Z| \cdot |Z'| = R^2\)，则 \(|Z'| = \dfrac{R^2}{|Z|}\)。又知 \(Z'\) 与 \(Z\) 同向，所以：

\[\begin{aligned} Z' &= \dfrac{Z}{|Z|} \cdot |Z'| \\ &= \dfrac{Z}{|Z|} \cdot \dfrac{R^2}{|Z|} \\ &= \dfrac{R^2 Z}{|Z|^2} \\ &= \dfrac{R^2 Z}{Z \cdot \overline{Z}} \\ &= \dfrac{R^2}{\overline{Z}} \\ \end{aligned} \]

\(O = 0\) 的情况结束了，接下来求任意 \(O \in \mathbb{C}\) 的情况。这个比较简单，就把 \(Z\) 换成 \(Z - O\)，把 \(Z'\) 换成 \(Z' - O\) 即可：

\[Z' - O = \dfrac{R^2}{\overline{Z - O}} \]

即：

\[Z' = \dfrac{R^2}{\overline{Z - O}} + O \]

坐标形式为：

\[\begin{cases} x_{Z'} = x_O + \dfrac{R^2 (x_Z - x_O)}{(x_Z - x_O)^2 + (y_Z - y_O)^2} \\ y_{Z'} = y_O + \dfrac{R^2 (y_Z - y_O)}{(x_Z - x_O)^2 + (y_Z - y_O)^2} \end{cases} \]

2.3.2 极线与极点

设点 \(A\) 关于 \(\odot O\) 的对称点为 \(A'\)，作 \(l \perp OA'\)，定义 \(l\) 为 \(\odot O\) 的极线，\(A\) 为该极线的极点。

3. 椭圆

3.1 定义

定义千千万，这里给出 2 种定义。

1. 给定 \(A, B\)，动点 \(P\) 满足 \(PA + PB\) 为定值，我们定义 \(P\) 的轨迹为椭圆，\(A, B\) 为这个椭圆的焦点。
2. 给定圆锥 \(\omega\) 和平面 \(\Omega\)，若 \(\Omega\) 不过 \(\omega\) 的底面，则定义 \(\omega\) 和 \(\Omega\) 的交线为椭圆。

对这两种定义等价的证明见此。

3.2 表示方法

3.2.1 标准方程

我们为了简单一点，令焦点 \(F_1 = (-f, 0), F_2 = (f, 0)\) 满足 \(f > 0\)。

设 \(P\) 在椭圆上，则 \(PF_1 + PF_2 = \sqrt{(x_P + f)^2 + y_P^2} + \sqrt{(x_P - f)^2 + y_P^2} = C\) 为定值。

化简得：

\[2fx_P = C^2 - 2fx_P - 2C \sqrt{(x_P - f)^2 + y_P^2} \]

则：

\[4C^2 x_P^2 + 4C^2 f^2 + 4C^2 y_P^2 = C^4 + 16 f^2 x_P^2 \]

整理得：

\[4 \left( C^2 - 4f^2 \right) x_P^2 + 4C^2 y_P^2 = C^2 \left( C^2 - 4f^2 \right) \]

两边除以 \(4C^2 \left( C^2 - 4f^2 \right)\)：

\[\dfrac{x_P^2}{C^2} + \dfrac{y_P^2}{C^2 - 4f^2} = \dfrac{1}{4} \]

想让等式右边为 \(1\)，这样更“标准”：

\[\dfrac{x_P^2}{C^2 / 4} + \dfrac{y_P^2}{C^2 / 4 - f^2} = 1 \]

注：此处 \(\dfrac{C^2}{4} - f^2\) 一定 \(> 0\)。证明：如果 \(< 0\)，则有 \(C < 2f \iff PF_1 + PF_2 < F_1 F_2\)，一定不合法。\(\square\)

令 \(a^2 = \dfrac{C^2}{4}, b^2 = \dfrac{C^2}{4} - f^2\)，则：

\[\dfrac{x_P^2}{a^2} + \dfrac{y_P^2}{b^2} = 1 \]

则椭圆的标准方程是：

\[\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \]

其中 \(a > b > 0\)。此时可知椭圆上任意一点到两焦点的距离和为 \(2a\)，且两焦点为 \(\left( \pm \sqrt{a^2 - b^2}, 0 \right)\)。

由标准方程还可以衍生出一些其他的概念。设椭圆 \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\) 交 \(x\) 轴于 \(P_1, P_2\)，交 \(y\) 轴于 \(Q_1, Q_2\)，焦点为 \(F_1, F_2\)。则定义该椭圆的长轴为 \(P_1 P_2\) 和 \(Q_1 Q_2\) 中更长的，短轴为两者中更短的，离心率（一般用 \(e\) 表示）为 \(F_1 F_2\) 与长轴的长度的比值，为 \(\dfrac{F_1 F_2}{2a}\)。

3.2.2 参数方程

将标准方程变形一下：

\[\left( \dfrac{x}{a} \right)^2 + \left( \dfrac{y}{b} \right)^2 = 1 \]

我们发现，这其实就是把单位圆在 \(x\) 轴上拉长了 \(a\) 倍，在 \(y\) 轴上拉长了 \(b\) 倍。则参数方程为：

\[\begin{cases} x = a \cos(t) \\ y = b \sin(t) \end{cases} \]

3.3 极线与极点

这部分的内容与切线密切相关。

我们尝试做椭圆 \(\Omega : \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\) 在 \(A = (x_0, y_0)\) 上的切线，满足 \(A\) 在 \(\Omega\) 上。

一个想法是求导。隐函数求导得：

\[\dfrac{2x}{a^2} \,{\rm d} x + \dfrac{2y}{b^2} \,{\rm d} y = 0 \]

则：

\[\dfrac{2x}{a^2} \,{\rm d} x = -\dfrac{2y}{b^2} \,{\rm d} y \]

即：

\[\dfrac{{\rm d} y}{{\rm d} x} = -\dfrac{2x / a^2}{2y / b^2} = -\dfrac{b^2 x}{a^2 y} \]

那么 \(A\) 处的切线的斜率为 \(k = -\dfrac{b^2 x_0}{a^2 y_0}\)。

设切线为 \(y = -\dfrac{b^2 x_0}{a^2 y_0} x + B\)，代入 \(A\) 的坐标得 \(B = y_0 + \dfrac{b^2 x_0^2}{a^2 y_0}\)。

则切线为 \(y = -\dfrac{b^2 x_0}{a^2 y_0} x + \left( y_0 + \dfrac{b^2 x_0^2}{a^2 y_0} \right)\)。化简得：

\[\begin{equation} \dfrac{x_0 x}{a^2} + \dfrac{y_0 y}{b^2} = 1 \end{equation} \]

注意到上述情况有 \(A\) 在 \(\Omega\) 上的限制，那如果去掉那个限制呢？你可以尝试求一下切线，但是这很困难。

注意到这时有 2 个切线，设它们分别交 \(\Omega\) 于 \(A_1 = (x_1, y_1), A_2 = (x_2, y_2)\)。我们可以尝试求一下 \(A_1 A_2\)。

注：这题比较诈骗，计算量基本没有。

我们知道 \(A_1 A : \dfrac{x_1 x}{a^2} + \dfrac{y_1 y}{b^2} = 1\) 和 \(A_2 A : \dfrac{x_2 x}{a^2} + \dfrac{y_2 y}{b^2} = 1\)。代入特殊值：

\[\begin{aligned} \dfrac{x_1 x_0}{a^2} + \dfrac{y_1 y_0}{b^2} &= 1 \\ \dfrac{x_2 x_0}{a^2} + \dfrac{y_2 y_0}{b^2} &= 1 \end{aligned} \]

这时我们声称 \(A_1 A_2 : \dfrac{x_0 x}{a^2} + \dfrac{y_0 y}{b^2} = 1\)。证明：由前文的两个等式，我们知道 \(A_1\) 和 \(A_2\) 都在 \(\dfrac{x_0 x}{a^2} + \dfrac{y_0 y}{b^2} = 1\) 上。因为两点确定一条直线，所以 \(A_1 A_2\) 一定是这条直线。\(\square\)

定义 \(A_1 A_2\) 为切点弦。发现 \((1)\) 式比较多见，所以我们定义它为极线，\(A\) 为极点。注意到，我们没有对 \(A\) 的位置作出限制，这意味着 \(A\) 可以在椭圆内部。

注：这里的定义和 2.3 节的有类似的性质。

4. 双曲线

4.1 定义

双曲线的定义和椭圆类似。给定 \(A, B\)，动点 \(P\) 满足 \(|PA - PB|\) 为定值，我们定义 \(P\) 的轨迹为双曲线，\(A, B\) 为这个双曲线的焦点。

4.2 表示方法

4.2.1 标准方程

设双曲线上有一点 \(P\)，焦点为 \(F_{1, 2} = (\pm f, 0)\)。推导过程与椭圆类似，最后可以得到：

\[\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1 \]

其中 \(a^2 = \dfrac{(PF_1 - PF_2)^2}{4}\) 为定值，\(b^2 = a^2 - f^2\)。

离心率的定义和椭圆相似。

4.2.2 参数方程

双曲线 \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\) 可以用下式表示：

\[\begin{cases} x = a \sec(t) \\ y = b \tan(t) \end{cases} \]

4.3 渐近线

双曲线 \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\) 是有渐近线的，怎么求呢？考虑待定系数，设渐近线为 \(y = kx + n\)。

但是双曲线的式子是隐函数，不好看。注意到由双曲线的对称性，我们只用看一半，所以取 \(x\) 轴以上的部分。则它的表达式为：

\[y = \sqrt{\dfrac{b^2 x^2}{a^2} - 1} \]

则有：

\[\lim_{x \to \infty} \left( \sqrt{\dfrac{b^2 x^2}{a^2} - 1} - kx - n \right) = 0 \]

移项得：

\[\lim_{x \to \infty} \left( \sqrt{\dfrac{b^2 x^2}{a^2} - 1} - \sqrt{k^2 x^2} \right) = n \]

注意到，\(\lim \limits_{x \to \infty} \left( \sqrt{ax + b} - \sqrt{cx + d} \right)\) 的值在 \(a \neq 0\) 或 \(c \neq 0\) 时只能为 \(0\) 或 \(\pm \infty\)。因为 \(n \in \mathbb{R}\) 而 \(\infty \notin \mathbb{R}\)，所以：

\[\lim_{x \to \infty} \left( \sqrt{\dfrac{b^2 x^2}{a^2} - 1} - \sqrt{k^2 x^2} \right) = n = 0 \]

则：

\[\begin{cases} k = \dfrac{b}{a} \\ n = 0 \end{cases} \]

那么渐近线为 \(y = \dfrac{b}{a} x\)。由对称性，\(y = -\dfrac{b}{a} x\) 也是渐近线。

例题

证明：反比例函数 \(y = \dfrac{k}{x}\) 是双曲线。

不妨设 \(k > 0\)。

首先，\(y = \dfrac{k}{x}\) 肯定不能写成标准方程的形式。但是它们都有两条渐近线，一个关于 \(y = -x\) 对称，一个关于 \(y\) 轴对称。

因为 \(y = -x\) 和 \(y\) 轴的夹角为 \(45 \degree\)，所以可以想到把 \(y = \dfrac{k}{x}\) 关于原点顺时针旋转 \(45 \degree\)。于是 \(\left( x, \dfrac{k}{x} \right)\) 变成了 \(\left( \dfrac{k + x^2}{\sqrt{2} x}, \dfrac{k - x^2}{\sqrt{2} x} \right)\)。

设 \(A = \dfrac{k + x^2}{\sqrt{2} x}, B = \dfrac{k - x^2}{\sqrt{2} x}\)，则 \(A^2 - B^2 = (A + B)(A - B) = \dfrac{2k}{\sqrt{2} x} \cdot \sqrt{2} x = 2k\)。

则 \(\dfrac{A^2}{2k} - \dfrac{B^2}{2k} = 1\)，则 \(\left( \dfrac{k + x^2}{\sqrt{2} x}, \dfrac{k - x^2}{\sqrt{2} x} \right)\) 在 \(\dfrac{x^2}{2k} - \dfrac{y^2}{2k} = 1\) 上。

故 \(y = \dfrac{k}{x}\) 关于原点顺时针旋转 \(45 \degree\) 后是双曲线。\(\square\)

5. 抛物线

5.1 定义

已知定点 \(F\) 和定直线 \(l\)，设动点 \(P\) 满足 \(\dfrac{FP}{\operatorname{dist}(P, l)} = 1\)，则定义 \(P\) 的轨迹为抛物线。容易发现，\(F\) 在 \(l\) 上时 \(P\) 的轨迹为直线，所以一般规定 \(F\) 不能在 \(l\) 上。

5.2 标准方程

先建系。实践证明，把 \(y\) 轴放到 \(l\) 和 \(F\) 的中间，把 \(x\) 轴放到 \(F\) 上是最好算的。于是设 \(F = (f, 0), l : x = -f\)，那么：

\[\begin{aligned} FP^2 &= (x_P - f)^2 + y_P^2 = x_P^2 + y_P^2 - 2f x_P + f^2 \\ \operatorname{dist}^2(P, l) &= (x_P + f)^2 = x_P^2 + 2f x_P + f^2 \end{aligned} \]

则：

\[x_P^2 + y_P^2 - 2f x_P + f^2 = x_P^2 + 2f x_P + f^2 \]

化简得：

\[y_P^2 - 2f x_P = +2f x_P \]

则：

\[y_P^2 = 4f x_P \]

因为 \(P\) 是动点，所以 \(P\) 的轨迹即为 \(y^2 = 4fx\)。这就是抛物线的标准方程。

当然，可以让抛物线开口朝上或下，此时标准方程就是 \(x^2 = 4fy\)，其实就是关于 \(y = x\) 对称了一下。

6. 圆锥曲线

6.1 定义

我们使用了 \(FP = \operatorname{dist}(P, l)\) 来定义抛物线，那如果加一个系数呢？

已知定点 \(F\) 和定直线 \(l\)，设动点 \(P\) 满足 \(\dfrac{FP}{\operatorname{dist}(P, l)} = e\)，则定义 \(P\) 的轨迹为圆锥曲线。当然，\(F\) 不能在 \(l\) 上。

定义 \(e\) 为圆锥曲线的离心率，\(l\) 为准线，\(F\) 为焦点。

注：为什么叫圆锥曲线？因为用平面切一个圆锥，交线一定是椭圆、双曲线、抛物线的一种。

6.2 求 \(FP\)

已知 \(P\) 的一些条件，我们考虑求出 \(FP\)。以下图举例，其他情况类似。

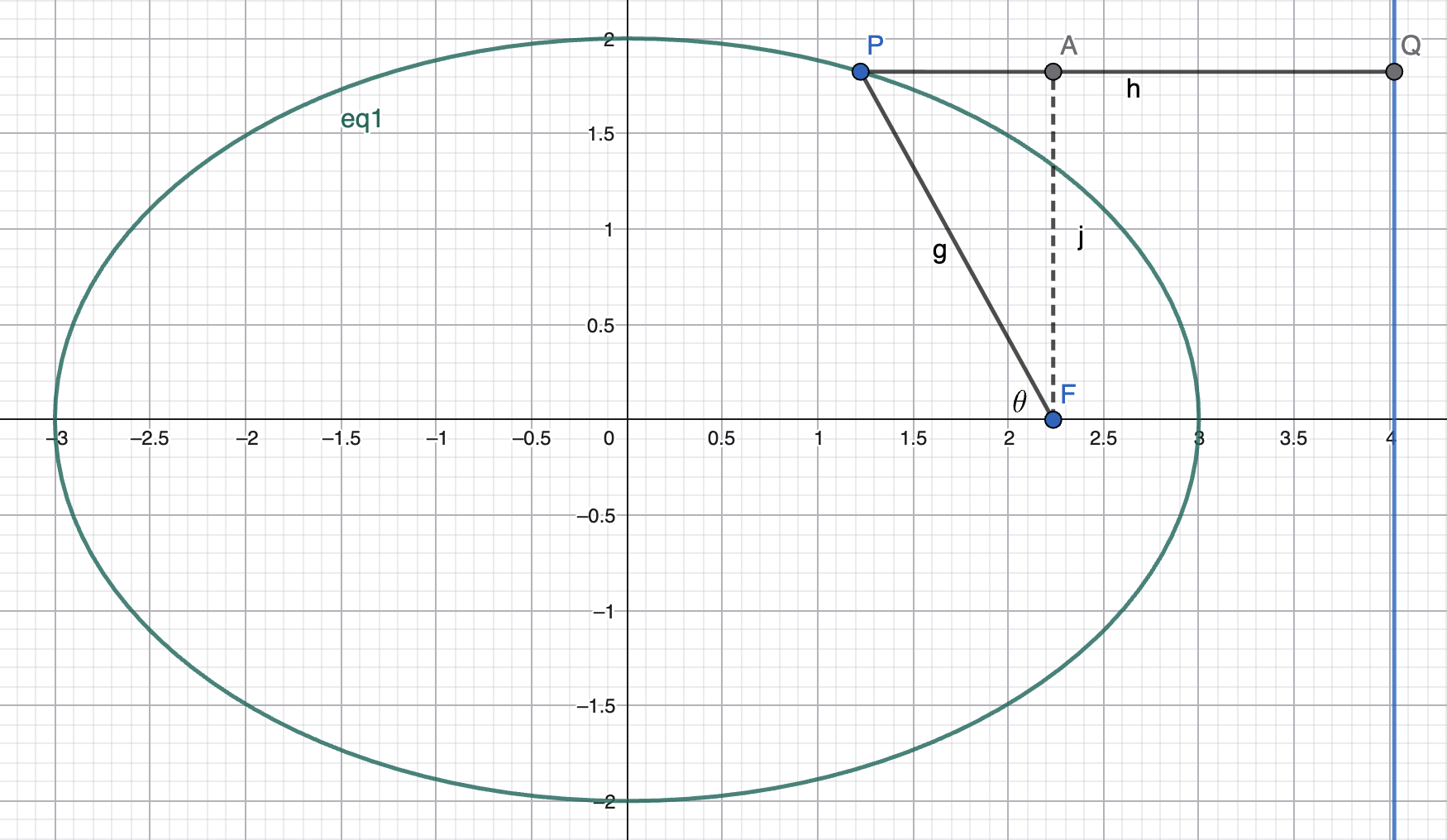
若我们知道 \(FP\) 与 \(x\) 轴的夹角 \(\theta\)，则可以做 \(AF \perp PQ\) 于 \(A\)。那么：

\[AP = FP \sin(\pi / 2 - \theta) = FP \cos(\theta) \]

设准线为 \(x = d\)，则 \(AQ = d - f\)，则：

\[PQ = AP + AQ = FP \cos(\theta) + d - f = \dfrac{FP}{e} \]

解得：

\[FP = \dfrac{e(f - d)}{e \cos(\theta) - 1} \]

若我们知道 \(P\) 的坐标，那就更简单了。此时 \(PQ = d - x_P\)，则：

\[FP = e \cdot PQ = e(d - x_P) \]

6.3 椭圆

6.3.1 定义

6.3.2 表示方法

6.3.3 离心率

6.3.4 准线

因为椭圆有 2 个焦点，所以有两个准线。我们只研究右准线，因为它们关于 \(y\) 轴对称。那么右准线在哪里呢？

设椭圆为 \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\)，焦点为 \(F = (f, 0)\)，右准线为 \(x = d\)。设 \(P = (a, 0)\)，则：

\[FP = e(d - x_P) = e(d - a) = \dfrac{f}{a} (d - a) = a - f \]

解得：

\[d = \dfrac{a^2}{f} \]

则右准线为 \(x = \dfrac{a^2}{f}\)，则两个准线为 \(x = \pm \dfrac{a^2}{f}\)。