微积分笔记

笔者还在学习中，所以笔记目前很不全，见谅。

记号约定：

• \(\mathbb{Q}\)：有理数集。
• \([\cdot]\)：Iverson 括号。
• \(\square\)：证毕。

更新记录：

• 2025.8.11：加入 1.1 ~ 1.4、2.1 ~ 2.6。
• 2025.9.2：加入 2.7。

1. 极限

1.1 定义

设数列 \(\{ a_n \}_{n \in \N}\)，当且仅当对于任意 \(\epsilon > 0\)，都存在 \(N \in \N\)，使得对于任意 \(n > N\)，都有 \(|a_n - A| < \epsilon\) 时，称 \(A\) 是该数列的极限，记作 \(\lim \limits_{n \to \infty} a_n = A\)。

当数列没有极限时，称该数列发散。

设函数 \(f(x)\) 在点 \(x_0\) 的某个去心邻域内有定义，如果对于任意给定的 \(\varepsilon > 0\)，都存在 \(\delta > 0\)，使得当 \(0 < |x - x_0| < \delta\) 时，都有 \(|f(x) - A| < \varepsilon\)，那么称 \(A\) 是 \(f(x)\) 当 \(x \to x_0\) 时的极限，记作 \(\lim \limits_{x \to x_0} f(x) = A\)。

当函数在 \(x \to x_0\) 没有极限时，称该函数在 \(x \to x_0\) 时发散。

注：\(\lim \limits_{x \to x_0} f(x)\) 与 \(f(x_0)\) 的值无关。如函数：

\[f(x) = \begin{cases} x + 1, &x \neq 1 \\ \pi &x = 1 \end{cases} \]

的极限 \(\lim \limits_{x \to 1} f(x) = 2\)，不等于 \(\pi\)。

上述定义要求 \(f(x)\) 在点 \(x_0\) 的去心邻域 \(D\) 内有定义，那如果把 \(D\) 中 \(> x_0\) 的部分去掉呢？于是我们得到了左极限，记作 \(\lim \limits_{x \to x_0^-} f(x)\)。同理，把 \(< x_0\) 的部分去掉，就得到了右极限，记作 \(\lim \limits_{x \to x_0^+} f(x)\)。

容易发现，若 \(\lim \limits_{x \to x_0^-} f(x) = \lim \limits_{x \to x_0^+} f(x) = A\)，则 \(\lim \limits_{x \to x_0} f(x) = A\)。在 \(\lim \limits_{x \to x_0^-} f(x) \neq \lim \limits_{x \to x_0^+} f(x)\) 时，\(\lim \limits_{x \to x_0} f(x)\) 不存在。

1.2 运算法则

设 \(c\) 是一个常数，且 \(\lim \limits_{x \to a} f(x)\) 和 \(\lim \limits_{x \to a} g(x)\) 存在，则有：

1. \(\lim \limits_{x \to a} (f(x) \pm g(x)) = \lim \limits_{x \to a} f(x) \pm \lim \limits_{x \to a} g(x)\)。
2. \(\lim \limits_{x \to a} (f(x) \cdot g(x)) = \lim \limits_{x \to a} f(x) \cdot \lim \limits_{x \to a} g(x)\)。
3. \(\lim \limits_{x \to a} \left( \dfrac{f(x)}{g(x)} \right) = \dfrac{\lim_{x \to a} f(x)}{\lim_{x \to a} g(x)} \quad \left( \lim \limits_{x \to a} g(x) \neq 0 \right)\)。
4. \(\lim \limits_{x \to a} (c \cdot f(x)) = c \cdot \lim \limits_{x \to a} f(x)\)。
5. \(\lim \limits_{x \to a} f^n(x) = \left( \lim \limits_{x \to a} f(x) \right)^n \quad (n \in \N^+)\)。
6. \(\lim \limits_{x \to a} \sqrt[n]{f(x)} = \sqrt[n]{\lim \limits_{x \to a} f(x)} \quad \left( n \in \N^+, 2 \nmid n \lor \lim \limits_{x \to a} f(x) \ge 0 \right)\)。

1.3 夹逼定理

本关考验你放缩能力。

对于函数 \(f(x)\) 和 \(x_0\)，若 \(f\) 在 \(x_0\) 的去心邻域中总有 \(g(x) \le f(x) \le h(x)\)，且 \(\lim \limits_{x \to x_0} g(x) = \lim \limits_{x \to x_0} h(x) = A\)，则 \(\lim \limits_{x \to x_0} f(x) = A\)。

例题 1

设：

\[f(x) = \begin{cases} x^2, &x \in \mathbb{Q} \\ 0, &x \in \mathbb{Q} \end{cases} \]

证明：\(\lim \limits_{x \to 0} f(x) = 0\)。

因为 \(x^2 \ge f(x) \ge 0\)，而 \(\lim \limits_{x \to 0} x^2 = \lim \limits_{x \to 0} 0 = 0\)，所以 \(\lim \limits_{x \to 0} f(x) = 0\)。\(\square\)

例题 2

构造 \(f(x)\) 和 \(g(x)\)，使得 \(\lim \limits_{x \to a} (f(x) + g(x))\) 和 \(\lim \limits_{x \to a} (f(x) \cdot g(x))\) 都存在，但 \(\lim \limits_{x \to a} f(x)\) 和 \(\lim \limits_{x \to a} g(x)\) 都不存在。

我们从例题 1 吸取灵感，令 \(f(x) = [x \in \mathbb{Q}], g(x) = 1 - f(x), a = 1\) 即可。\(\square\)

1.4 连续性与极限

定义 \(f(x)\) 在 \(x = c\) 处连续，当且仅当 \(\lim \limits_{x \to c} f(x) = f(c)\)。

注：还有一种充要条件：\(\lim \limits_{h \to 0} f(c + h) = f(c)\)，这个可以和导数联合使用。

容易发现，若 \(f(x), g(x)\) 都在 \(x = c\) 处连续，则 \(f(x) \pm g(x)\)、\(a \cdot f(x)\) 和 \(f(x) \cdot g(x)\) 也在此处连续，但是 \(\dfrac{f(x)}{g(x)}\) 仅在 \(g(c) \neq 0\) 时在此处连续。

那如果把它俩复合呢？先让 \(f\) 处处连续，考虑求 \(\lim \limits_{x \to c} f(g(x))\)。直观上，此时 \(g(x)\) 应该取到 ^[1] \(\lim \limits_{x \to c} g(x)\)，那么 \(\lim \limits_{x \to c} f(g(x)) = f \left( \lim \limits_{x \to c} g(x) \right)\)。

证明暂时不会。

那么当 \(\lim \limits_{x \to c} g(x) = g(c)\) 时，\(\lim \limits_{x \to c} f(g(x)) = f(g(c))\)，那么 \(f(g(x))\) 在 \(x = c\) 处连续。我们发现，好像不需要那么多条件，只需让 \(g\) 在 \(x = c\) 处连续，且 \(f\) 在 \(g(c)\) 处连续即可。

介值定理

若 \(f(x)\) 在 \([a, b]\) 上连续，且 \(f(a) \neq f(b)\)，则对于任意在 \(f(a)\) 和 \(f(b)\) 之间的 \(N\)，总存在 \(c \in (a, b)\) 满足 \(f(c) = N\)。

实际上，对于任意符合条件的 \(N\)，我们可以使用二分法找到一个 \(c\)：

0. 不妨设 \(f(a) < N < f(b)\)。
1. 初始化 \(l = a, r = b\)。
2. 计算 \(m = \dfrac{l + r}{2}\)。
3. 若 \(f(m) < N\)，令 \(l \gets m\)；否则令 \(r \gets m\)。
4. 回到第 2 步。

容易发现，在步数趋近于 \(+\infty\) 时 \(r - l \to 0\)。证明：每一次循环会让 \(r - l\) 减半，且初始时 \(r - l = b - a\)，而 \(\lim \limits_{n \to \infty} \left( \dfrac{b - a}{2^n} \right) = 0\)。\(\square\)

那在步数趋近于 \(+\infty\) 时，我们可以令 \(l = r\)。又知在任意时刻，\(f(l) < N < f(r)\) ^[2]，所以此时 \(f(l) = f(r) = N\)。此时我们要找的 \(c = l\)。

二分没想到，OI 白学了。

它的逆定理显然不成立，反例：

\[f(x) = \begin{cases} x, &x \in \mathbb{Q} \\ x^2, &x \notin \mathbb{Q} \end{cases} \]

容易发现，\(f\) 在 \([0, 1]\) 内满足介值性。证明：若 \(c \in \mathbb{Q}\)，\(f(c) = c\)；否则 \(\sqrt{c} \notin \mathbb{Q}\)，且 \(f \left( \sqrt{c} \right) = c\)。\(\square\)

也容易发现，\(f\) 在 \([0, 1]\) 内不连续。证明 ^[3]：对于无理数 \(x_0 \in (0, 1)\)，取有理数序列 \(\{ x_n \}\) 满足 \(x_n \to x_0\)，则 \(f(x_n) = x_n \to x_0\)，则 \(\lim \limits_{n \to \infty} f(x_n) = x_0 \neq x_0^2 = f(x_0)\)。\(\square\)

故 \(f\) 是反例。

例题 1

若 \(f(x)\) 在区间 \([a, b]\) 上连续，证明：\(|f|\) 在 \([a, b]\) 上也连续。

设 \(f\) 的零点是 \(r_1 < r_2 < \ldots < r_n\)，可以把 \(f\) 写成分段函数的形式：

\[f(x) = \begin{cases} g_0(x), &a \le x < r_1 \\ g_1(x), &r_1 \le x < r_2 \\ g_2(x), &r_2 \le x < r_3 \\ \vdots \\ g_{n - 1}(x), &r_{n - 1} \le x < r_n \\ g_n(x) &r_n \le x \le b \end{cases} \]

容易发现，\(\lim \limits_{x \to r_i} g_{i - 1}(x) = \lim \limits_{x \to r_i} g_i(x) = 0\)。

接着分析绝对值。我们发现，给 \(f\) 套上绝对值，会翻转 \(g\) 中一些函数的符号。但是 \(\lim \limits_{x \to r_i} g_i(x) = \lim \limits_{x \to r_i} -g_i(x) = 0\)，所以翻转符号不改变极限的值。那么 \(\lim \limits_{x \to r_i} |g_{i - 1}(x)| = \lim \limits_{x \to r_i} |g_i(x)| = 0\)。\(\square\)

2. 导数

2.1 定义

有一辆车在 \(t\) 时刻行驶的路程为 \(x(t)\)，那么可以算出它在时刻 \([l, r]\) 的平均速度：

\[\bar{v}(l, r) = \dfrac{x(r) - x(l)}{r - l} \]

那如何求它在时刻 \(t\) 的瞬时速度呢？首先，肯定不能用 \(\bar{v}(t, t)\) 来算，因为分母会变成 \(0\)。

那我们牺牲一点精度，用 \(\bar{v}(t, t + h)\) 来算，其中 \(h\) 要取得很小。不难发现，\(h\) 越小，精度越高。那么当 \(h \to 0\) 时，精度是无穷高，那不就是准确值吗？

于是，它在时刻 \(t\) 的瞬时速度为：

\[v(t) = \lim \limits_{h \to 0} \bar{v}(t, t + h) = \lim \limits_{h \to 0} \left( \dfrac{x(t + h) - x(t)}{h} \right) \]

恭喜你！你发明了导数。

我们定义 \(f(x)\) 的导数为 \(\lim \limits_{h \to 0} \left( \dfrac{f(x + h) - f(x)}{h} \right)\)，记作 \(f'(x)\) 或 \(\dfrac{{\rm d} f}{{\rm d} x}\)。考虑做切线的过程，可以发现，\(f'(x_0)\) 是 \(f\) 在 \(x_0\) 处的切线的斜率。

注：可以把 \({\rm d} f\) 理解成 \(f\) 的微小变化量，\({\rm d} x\) 同理。因为 \(\dfrac{{\rm d} f}{{\rm d} x} = f'(x)\)，所以 \({\rm d} f = f'(x) {\,\rm d} x\)。

注意到，\(f'(x)\) 也是函数，那么它可能也会有自己的导数 \(f''(x)\)，定义为 \(f\) 的二阶导数。于是，我们定义 \(f\) 的 \(n\) 阶导数为 \(f\) 求 \(n\) 次导后的结果，记为 \(f^{(n)}(x)\) 或 \(\dfrac{{\rm d}^n f}{{\rm d} x^n}\)。形式化的：

\[\begin{cases} f^{(1)}(x) = f'(x) \\ f^{(n)}(x) = \left( f^{(n - 1)}(x) \right)' \end{cases} \]

或：

\[\dfrac{{\rm d}^n f}{{\rm d} x^n} = \dfrac{{\rm d}}{{\rm d} x} \left( \dfrac{{\rm d}^{n - 1} f}{{\rm d} x^{n - 1}} \right) \]

2.2 连续性与导数

若 \(f(x)\) 在 \(x = a\) 处可导，那么 \(f\) 在此处连续。

证明：条件说 \(f\) 可导，那么我们就求个导：

\[f'(a) = \lim \limits_{h \to 0} \left( \dfrac{f(a + h) - f(a)}{h} \right) \]

注意到：

\[f(a + h) - f(a) = \dfrac{f(a + h) - f(a)}{h} \cdot h \]

两边求极限：

\[\lim \limits_{h \to 0} (f(a + h) - f(a)) = \lim \limits_{h \to 0} \left( \dfrac{f(a + h) - f(a)}{h} \right) \cdot \lim \limits_{h \to 0} h = f'(a) \cdot 0 = 0 \]

则 \(\lim \limits_{h \to 0} f(a + h) = f(a)\)。\(\square\)

那么 \(f(x)\) 在 \(x = a\) 处连续，可以说明 \(f\) 在此处可导吗？不可以。\(f(x) = |x|\) 在 \(x = 0\) 处连续，但不可导。

但是，不连续的函数一定不可导。

2.3 运算法则

设 \(f(x), g(x)\) 可导，\(c\) 为任意常数，则有：

1. \((f \pm g)' = f' \pm g'\)。
2. \((f \cdot g)' = f \cdot g' + f' \cdot g\)。
3. \(\left( \dfrac{f}{g} \right)' = \dfrac{f' \cdot g - f \cdot g'}{g^2}\)。
4. \((f \circ g)' = f'(g) \cdot g'\) 或 \(\dfrac{{\rm d} f}{{\rm d} x} = \dfrac{{\rm d} f}{{\rm d} g} \cdot \dfrac{{\rm d} g}{{\rm d} x}\)。

2.4 特殊函数的导数 I

2.4.1 常数

这有点简单了。

设 \(c\) 是常数，很明显 \(y = c\) 的斜率是 \(0\)，那它在任意一点上的切线的斜率也是 \(0\)。

这说明 \(\dfrac{{\rm d}}{{\rm d} x} (c) = 0\)。

2.4.2 幂函数

开始上强度了，但不多。需要注意：幂函数的指数一定是整数。

设 \(n > 0\)，我们直接套定义：

\[\begin{aligned} \dfrac{{\rm d}}{{\rm d} x} \left( x^n \right) &= \lim \limits_{h \to 0} \left( \dfrac{(x + h)^n - x^n}{h} \right) \\ &= \lim \limits_{h \to 0} \left( \dfrac{x^n + nx^{n - 1} h + \sum \limits_{i = 2}^n \dbinom{n}{i} h^i x^{n - i} - x^n}{h} \right) \\ &= \lim \limits_{h \to 0} \left( nx^{n - 1} + \sum \limits_{i = 2}^n \dbinom{n}{i} h^{i - 1} x^{n - i} \right) \\ &= \lim \limits_{h \to 0} \left( nx^{n - 1} \right) + \lim \limits_{h \to 0} \left( \sum \limits_{i = 2}^n \dbinom{n}{i} h^{i - 1} x^{n - i} \right) \\ &= nx^{n - 1} + \lim \limits_{h \to 0} \left( \sum \limits_{i = 2}^n \dbinom{n}{i} h^{i - 1} x^{n - i} \right) \\ \end{aligned} \]

因为后面的和式中每一项都有 \(h\)，而 \(h \to 0\)，所以每一项都趋近于 \(0\)，那加起来也趋近于 \(0\)。

所以 \(\dfrac{{\rm d}}{{\rm d} x} \left( x^n \right) = nx^{n - 1} \quad (n > 0)\)。

在 \(n < 0\) 时，\(x^n = \dfrac{1}{x^{-n}}\)，使用 \(n > 0\) 的公式 + 2.3 节的第 4 条公式即可。

2.4.3 三角函数

你现在需要好好使用你的大脑。

以 \(\sin(x)\) 举例：

\[\begin{aligned} \sin'(x) &= \lim \limits_{h \to 0} \left( \dfrac{\sin(x + h) - \sin(x)}{h} \right) \\ &= \lim \limits_{h \to 0} \left( \dfrac{\sin(x) \cos(h) + \cos(x) \sin(h) - \sin(x)}{h} \right) \\ &= \lim \limits_{h \to 0} \left( \dfrac{\sin(x) \cos(h) - \sin(x)}{h} + \dfrac{\cos(x) \sin(h)}{h} \right) \\ &= \lim \limits_{h \to 0} \left( \dfrac{\cos(h) - 1}{h} \cdot \sin(x) + \dfrac{\sin(h)}{h} \cdot \cos(x) \right) \\ &= \lim \limits_{h \to 0} \left( \dfrac{\cos(h) - 1}{h} \right) \cdot \lim \limits_{h \to 0} \sin(x) + \lim \limits_{h \to 0} \left( \dfrac{\sin(h)}{h} \right) \cdot \lim \limits_{h \to 0} \cos(x) \\ \end{aligned} \]

那么如何求 \(A = \lim \limits_{h \to 0} \left( \dfrac{\cos(h) - 1}{h} \right)\) 和 \(B = \lim \limits_{h \to 0} \left( \dfrac{\sin(h)}{h} \right)\) 呢？

以 \(B\) 举例。如图，\(h = \overparen{AC}\)，则 \(\sin(h) = AB\)。

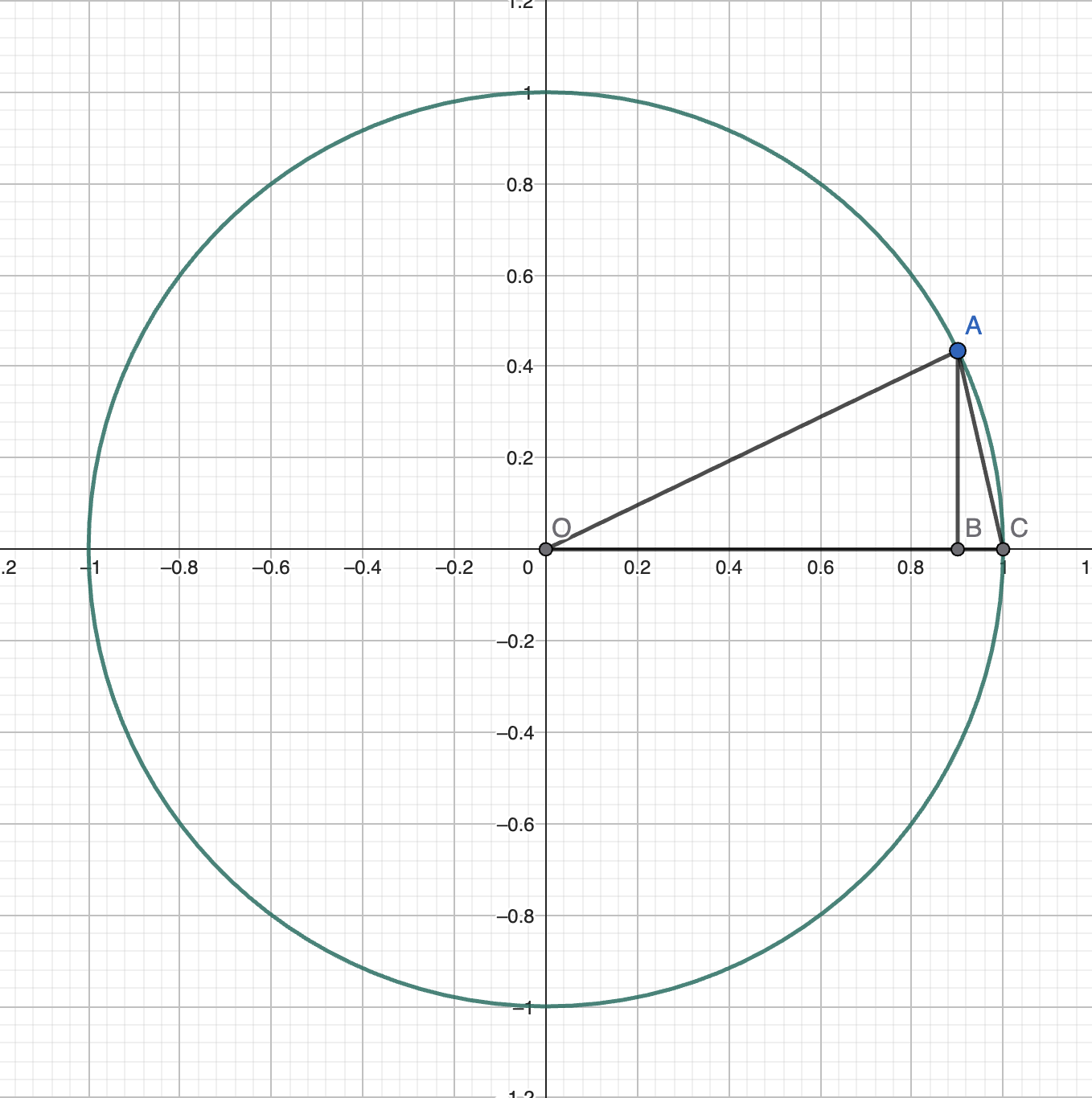
注意到，随着 \(h \to 0\)，\(AC \to \overparen{AC}\)，那我们只需研究 \(\dfrac{AB}{AC} = \cos(\angle BAC)\) 即可。

因为 \(A, C\) 都在单位圆上，所以 \(OA = OC\)，作 \(OD \perp AC\)，可知 \(\dfrac{\angle AOC}{2} = \dfrac{h}{2} = \angle CAD = \angle BAC\)，故 \(\dfrac{AB}{AC} = \cos(h / 2)\)。

又因为 \(h \to 0\)，所以 \(h / 2 \to 0\)，所以 \(\cos(h / 2) \to 1\)，所以 \(\dfrac{AB}{AC} \to 1\)。

于是 \(B = 1\)，现在求 \(A\)。如上图，\(\cos(h) - 1 = -BC\)，则 \(A = \lim \limits_{h \to 0} \left( -\dfrac{BC}{AC} \right) = \lim \limits_{h \to 0} -\sin(h / 2) = 0\)。

故：

\[\begin{aligned} \sin'(x) &= \lim \limits_{h \to 0} \left( \dfrac{\cos(h) - 1}{h} \right) \cdot \lim \limits_{h \to 0} \sin(x) + \lim \limits_{h \to 0} \left( \dfrac{\sin(h)}{h} \right) \cdot \lim \limits_{h \to 0} \cos(x) \\ &= 0 \cdot \lim \limits_{h \to 0} \sin(x) + 1 \cdot \lim \limits_{h \to 0} \cos(x) \\ &= \cos(x) \end{aligned} \]

对 \(1 - \sin^2(x)\) 求导可得 \(\cos'(x) = -\sin(x)\)，那么 \(\tan'(x) = \sec^2(x)\)。

我们发现，\(\sin\) 求导变成 \(\cos\)，\(\cos\) 求导变成 \(-\sin\)，几乎变回来了。

多求导几次：\(\sin \to \cos \to -\sin \to -\cos \to \sin \to \cdots\)。哇！上诱导公式：

\[\sin^{(n)}(x) = \sin(x + n \pi / 2) \\ \cos^{(n)}(x) = \cos(x + n \pi / 2) \]

2.5 隐函数求导

给定一单位圆 \(x^2 + y^2 = 1\)，我们想知道 \(x\) 变化时 \(y\) 如何变化，即 \(\dfrac{{\rm d} y}{{\rm d} x}\)，怎么办呢？

对等式两边求导：

\[2x \,{\rm d} x + 2y \,{\rm d} y = 0 \]

解得：

\[\dfrac{{\rm d} y}{{\rm d} x} = -\dfrac{x}{y} \]

这样的方法被称为隐函数求导，因为这里 \(y\) 是 \(x\) 的隐函数，并不是函数。

2.6 特殊函数的导数 II

2.6.1 指数函数

我们尝试求 \(\dfrac{{\rm d}}{{\rm d} x} \left( 2^x \right)\)。

使用定义：

\[\begin{aligned} \dfrac{{\rm d}}{{\rm d} x} \left( 2^x \right) &= \lim \limits_{h \to 0} \left( \dfrac{2^{x + h} - 2^x}{h} \right) \\ &= \lim \limits_{h \to 0} \left( \dfrac{2^x 2^h - 2^x}{h} \right) \\ &= \lim \limits_{h \to 0} 2^x \cdot \lim \limits_{h \to 0} \left( \dfrac{2^h - 1}{h} \right) \\ &= 2^x \cdot \lim \limits_{h \to 0} \left( \dfrac{2^h - 1}{h} \right) \end{aligned} \]

这个极限怎么求啊？我们先令 \(h\) 为一个很小的数来实际计算一下。

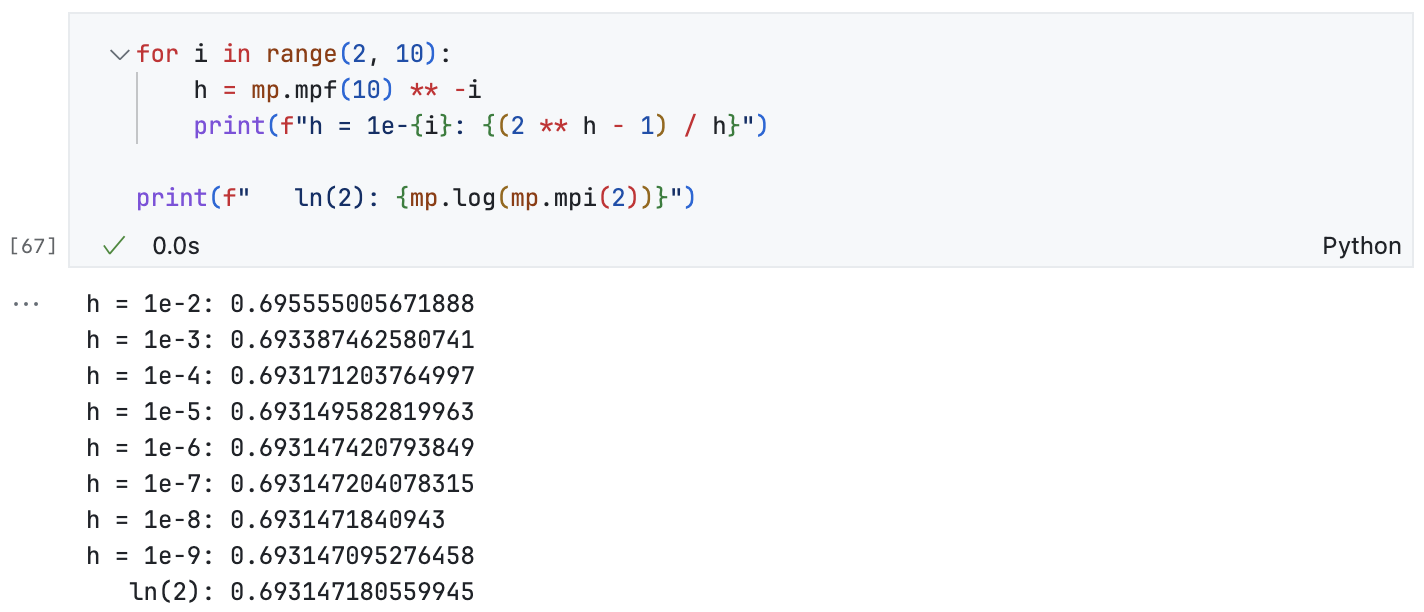
这里使用了高精度库 mpmath（代码中是 mp）。我们惊人的发现，随着 \(h\) 越来越小，\(\dfrac{2^h - 1}{h}\) 和 \(\ln(2)\) 越来越接近。于是我们猜测：\(\lim \limits_{h \to 0} \left( \dfrac{2^h - 1}{h} \right) = \ln(2)\)。

证明：既然有一个 \(\ln\)，那先凑一个 \(\ln\) 出来。

设 \(k = 2^h - 1\)，则 \(h = \log_2(k + 1) = \dfrac{\ln(k + 1)}{\ln(2)}\)，则：

\[\begin{aligned} \lim_{h \to 0} \left( \dfrac{2^h - 1}{h} \right) &= \lim_{k \to 0} \left( \dfrac{k \ln(2)}{\ln(k + 1)} \right) \\ &= \ln(2) \cdot \lim_{k \to 0} \left( \dfrac{1}{\dfrac{1}{k} \ln(k + 1)} \right) \\ &= \ln(2) \cdot \lim_{k \to 0} \left( \dfrac{1}{\ln \left( (k + 1)^{1 / k} \right)} \right) \\ &= \ln(2) \cdot \dfrac{1}{\ln \left( \lim \limits_{k \to 0} (k + 1)^{1 / k} \right)} \\ &= \ln(2) \cdot \dfrac{1}{\ln(e)} \\ &= \ln(2) \\ \end{aligned} \]

\(\square\)

于是 \(\dfrac{{\rm d}}{{\rm d} x} \left( 2^x \right) = 2^x \ln(2)\)，用类似的方法可知 \(\dfrac{{\rm d}}{{\rm d} x} \left( a^x \right) = a^x \ln(a)\)。注意到，\(a = e\) 时比较简单，因为 \(\ln(e) = 1\)，所以 \(\dfrac{{\rm d}}{{\rm d} x} \left( e^x \right) = e^x\)。

故以后遇到指数函数，一般都会把它变成以 \(e\) 为底。虽然以后见到的指数函数，一般都是以 \(e\) 为底。

2.6.2 对数函数

我们想对 \(y = \ln(x)\) 求导，即求 \(\dfrac{{\rm d} y}{{\rm d} x}\)。猜猜为什么要写成这样？

虽然我们不会对 \(\ln\) 求导，但我们会对 \(e^x\) 求导。又知 \(e^y = x\)，使用隐函数求导可得：

\[e^y \,{\rm d} y = 1 \,{\rm d} x \]

即：

\[\dfrac{{\rm d} y}{{\rm d} x} = \dfrac{1}{e^y} = \dfrac{1}{x} \]

所以 \(\ln'(x) = \dfrac{1}{x}\)，那么 \(\log_a'(x) = \left( \dfrac{\ln(x)}{\ln(a)} \right)' = \dfrac{1}{x \ln(a)}\)。

2.7 应用

2.7.1 函数的极值

当存在 \(l < r < c\) 满足 \(\forall x \in (l, r), f(x) \le f(c)\) 时，我们称 \(f(c)\) 为 \(f\) 的局部最大值。类似地定义局部最小值。

我们很难找局部最值。那就反过来，研究局部最值的性质。

以局部最大值举例，设 \(f(x)\) 的局部最大值为 \(f(c)\)，则 \(f(c)\) 为 \(f\) 在某一个区间 \((l, r)\) 的最大值，则 \(\forall h \in (l - c, r - c), f(c) \ge f(c + h)\)，则 \(f(c + h) - f(c) \le 0\)。

这与导数的性质很接近了，两边除以 \(h\)：

• \(h > 0\)：此时 \(\dfrac{f(c + h) - f(c)}{h} \le 0 \implies \lim \limits_{h \to 0^+} \left( \dfrac{f(c + h) - f(c)}{h} \right) \le 0\)。为了可以使用导数的定义，我们令 \(f'(c)\) 存在，则：

  \[f'(c) = \lim \limits_{h \to 0} \left( \dfrac{f(c + h) - f(c)}{h} \right) = \lim \limits_{h \to 0^+} \left( \dfrac{f(c + h) - f(c)}{h} \right) \le 0 \]

• \(h < 0\)：这种情况与 \(h > 0\) 对称，于是可以得到 \(f'(c) \ge 0\)。

综上，\(f'(c) = 0\)。局部最小值同理。

那它的逆定理成立吗？不成立，而且反例出奇的简单：\(f(x) = x^3\)，此时 \(f'(x) = 3x^2\)，于是 \(f'(0) = 0\)。但是 \(f(0)\) 并不是局部最值：\(\forall x > 0, f(-x) < f(0) < f(x)\)。

所以通过解 \(f'(x) = 0\) 的办法找出的局部最值不一定对，需要验证。但即使不对，这些点还是有用的，所以我们称其为临界点。

2.7.2 中值定理

设 \(f(x)\) 满足：

1. \(f\) 在 \([a, b]\) 上连续。
2. \(f\) 在 \((a, b)\) 上可导。
3. \(f(a) = f(b)\)。

则 \(\exists c \in (a, b), f'(c) = 0\)。

证明：我们考虑 \(f\) 在 \((a, b)\) 上的极值点。

• \(\exists c \in (a, b), f(c) > f(a)\)：则 \(f\) 在 \((a, b)\) 上的最大值 \(> f(a)\)。设该最大值为 \(m\)，则 \(f(m)\) 为局部最大值，则 \(f'(m) = 0\)。
• \(\exists c \in (a, b), f(c) < f(a)\)：则 \(f\) 在 \((a, b)\) 上的最小值 \(< f(a)\)。设该最小值为 \(m\)，则 \(f(m)\) 为局部最小值，则 \(f'(m) = 0\)。
• 否则：\(f(x)\) 在 \((a, b)\) 上为常数函数，导数处处为 \(0\)。

\(\square\)

这个定理叫做 Rolle 定理。

第 3 个条件能不能去掉呢？这样就足够一般了。

我们随便画一个满足条件 1 和 2 的函数图像，把两端点 \(A, B\) 连起来，发现好像总可以找到 \(P\) 满足过 \(P\) 的切线 \(l \parallel AB\)。

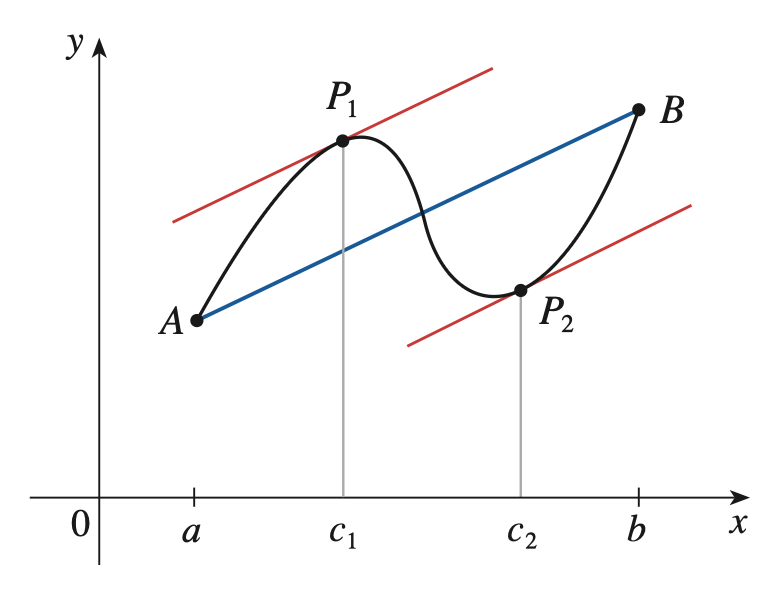
即 \(\exists c \in (a, b), f'(c) = \dfrac{f(b) - f(a)}{b - a}\)。

证明：设 \(AB : g(x) = \dfrac{f(b) - f(a)}{b - a} x + C\)。

显然 \(f(a) = g(a), f(b) = g(b)\)，即 \(f(a) - g(a) = f(b) - g(b) = 0\)。这启发我们换元，令 \(h(x) = f(x) - g(x)\)，则 \(h'(x) = f'(x) - g'(x) = f'(x) - \dfrac{f(b) - f(a)}{b - a}\)。

由 Rolle 定理，\(\exists c \in (a, b), h'(c) = f'(c) - \dfrac{f(b) - f(a)}{b - a} = 0\)。\(\square\)

2.7.3 凹凸性

在区间 \((l, r)\) 中，我们称：

• \(f(x)\) 上凸，当且仅当 \(\forall a, b \in (l, r), f \left( \dfrac{a + b}{2} \right) > \dfrac{f(a) + f(b)}{2}\)。
• \(f(x)\) 下凸，当且仅当 \(\forall a, b \in (l, r), f \left( \dfrac{a + b}{2} \right) < \dfrac{f(a) + f(b)}{2}\)。

结合图像，我们发现上凸就是图像比端点的连线高，下凸恰好相反。

在向量中，若 \(\exists \alpha, \overrightarrow{OC} = \alpha \cdot \overrightarrow{OA} + (1 - \alpha) \cdot \overrightarrow{OB}\)，则 \(A, B, C\) 共线。所以我们可以改进定义：

• \(f(x)\) 上凸，当且仅当 \(\forall \alpha \in (0, 1), f( \alpha \cdot l + (1 - \alpha) \cdot r) > \alpha \cdot f(l) + (1 - \alpha) \cdot f(r)\)。
• \(f(x)\) 下凸，当且仅当 \(\forall \alpha \in (0, 1), f( \alpha \cdot l + (1 - \alpha) \cdot r) < \alpha \cdot f(l) + (1 - \alpha) \cdot f(r)\)。

那么如何判定凹凸性呢？根据图像，我们发现上凸时 \(f'\) 单调减，下凸时相反。

如何描述 \(f'\) 的单调性呢？很简单，用 \(f''\)。于是，在区间 \((l, r)\) 中：

• 若 \(\forall a \in (l, r), f''(a) < 0\)，则 \(f\) 上凸。
• 若 \(\forall a \in (l, r), f''(a) > 0\)，则 \(f\) 下凸。

2.7.4 函数图像

如何画出 \(f(x)\) 准确的图像？首先要搞清楚 \(f\) 的性质。

1. 定义域：重要性不言而喻。没有这个，图像画着画着就没有定义了。
2. 特殊点：与坐标轴的交点、临界点等。
3. 对称性：可以让工作量减半，甚至更多。
4. 渐近线：这样可以画准边界值。
5. 单调性：重要性不言而喻，没有这个都不知道怎么画。
6. 凹凸性：让图像的细节更准确。

2.7.5 Newton-Raphson 迭代法

在生活中，我们常常想求出 \(f(x)\) 的根的数值（如开根号时），这时 Newton-Raphson 迭代法就派上用场了。

这个方法基于调整法，所以我们需要先猜一个根 \(x_0\)。

然后开始调整。往哪里调整会更接近根呢？我们作 \(f\) 在 \((x_0, f(x_0))\) 的切线 \(l\)，然后把 \(x_0\) 调整到 \(l\) 的根 \(x_1\)，一直进行下去。

于是我们有：

\[x_{n + 1} = x_n - \dfrac{f(x_n)}{f'(x_n)} \]

容易发现，这个方法在 \(f\) 比较陡时收敛速度不快，但比较缓时就很快了。而且，这个方法不保证一定能找到根 ^[4]，所以选对 \(x_0\) 很重要。

3. 积分

3.1 定积分

3.1.1 定义

在区间 \([a, b]\) 中，令 \(f(x) \ge 0\)，我们想要求 \(f\) 下方的面积，即 \(S\)。

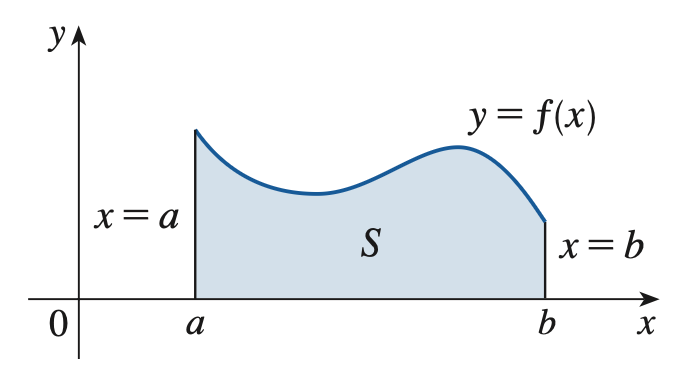
回忆一下我们是如何求复杂多边形的面积的。如下图，我们把多边形切成一个个小的三角形，然后把这些小三角形的面积加起来。

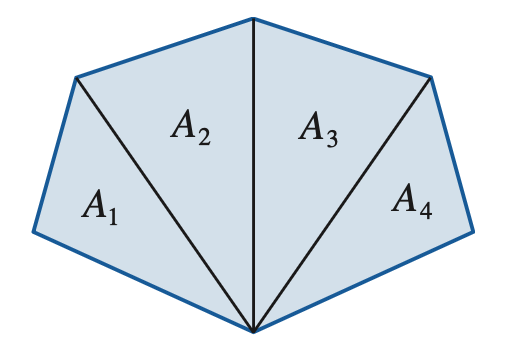
我们迁移一下，把 \(S\) 切成一个个小长条，然后把这些面积加起来。

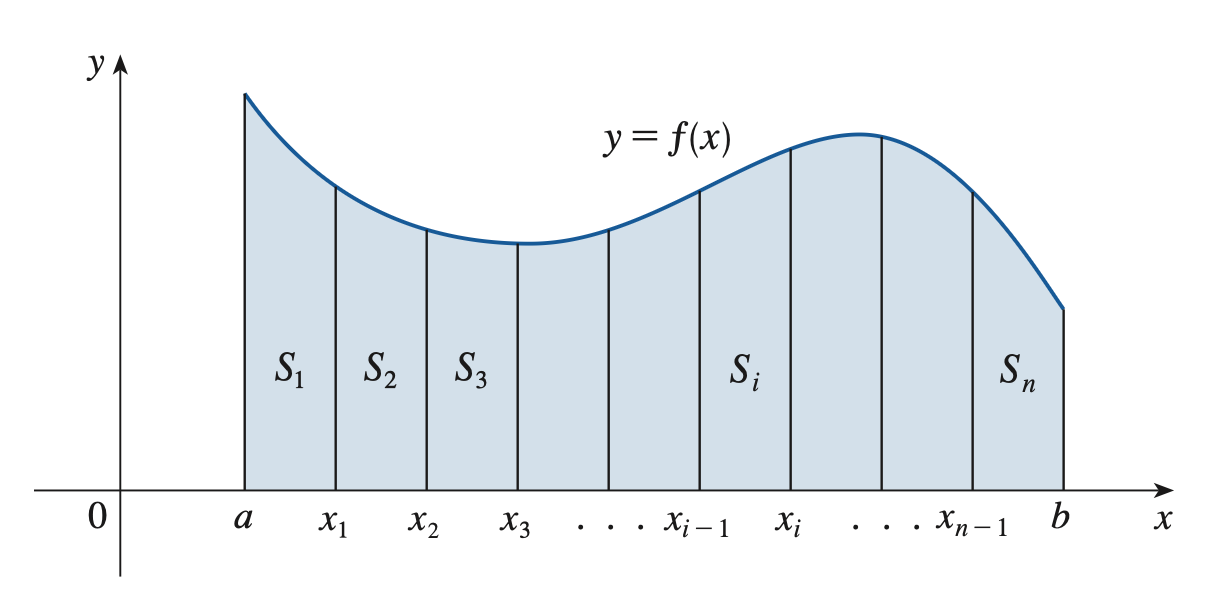
长条的面积过于难算，所以把它们近似成长方形，以右边作为长方形的边。（其实左边也行）

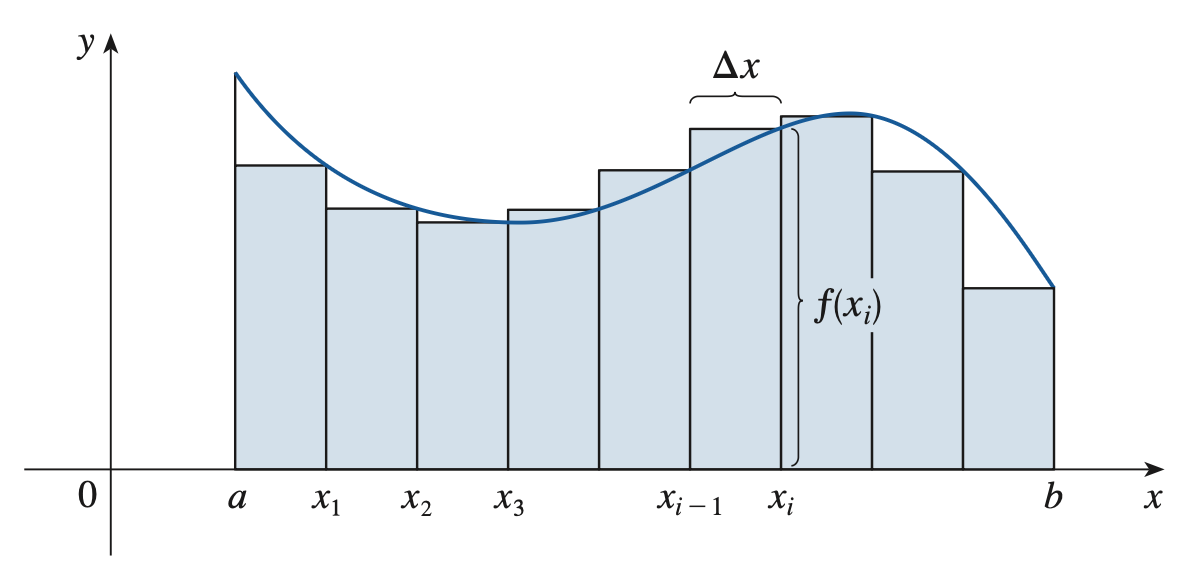
这时就可以算面积了：

\[S = \sum_{i = 1}^n f(x_i) \Delta x \]

其中 \(\Delta x = \dfrac{b - a}{n}, x_i = a + i \cdot \Delta x\)。恭喜你！你发明了定积分。我们定义：

\[\int_a^b f(x) \,{\rm d} x = \lim_{n \to \infty} \sum_{i = 1}^n f(x^*_i) \Delta x \quad (x_{i - 1} \le x^*_i \le x_i) \]

当然，这个极限需要存在，且对于任意的 \(x^*_i\)，这个极限的值需要保持不变。

还没完，如果 \(f(x)\) 不一定 \(\ge 0\) 怎么办？这时我们定义 \(\int_a^b f(x) \,{\rm d} x\) 为 \(x\) 轴上面的面积减去下面的面积。

在近似计算时，一般令 \(x^*_i = x_i\) 或 \(x^*_i = \dfrac{x_{i - 1} + x_i}{2}\)。

我们发现，这样定义积分，没有对 \(a, b\) 的限制，意味着 \(a > b\) 也合法。此时 \(\int_a^b f(x) \,{\rm d} x = -\int_b^a f(x) \,{\rm d} x\)。当然，\(\int_a^a f(x) \,{\rm d} x = 0\)。

3.1.2 存在条件

如果 \(f(x)\) 在 \([a, b]\) 上连续，或只有有限个断点，则 \(f\) 在 \([a, b]\) 上可积。

证明暂时不会。

3.1.3 运算法则

\(\int\) 和 \(\sum\) 类似，好多法则都比较类似。

1. \(\displaystyle \int_a^b c \,{\rm d} x = c(b - a)\)。
2. \(\displaystyle \int_a^b (f(x) \pm g(x)) \,{\rm d} x = \int_a^b f(x) \,{\rm d} x \pm \int_a^b g(x) \,{\rm d} x\)。
3. \(\displaystyle \int_a^b c \cdot f(x) \,{\rm d} x = c \int_a^b f(x) \,{\rm d} x\)。
4. \(\displaystyle \int_a^b f(x) \,{\rm d} x + \int_b^c f(x) \,{\rm d} x = \int_a^c f(x) \,{\rm d} x\)。
5. 若 \(\forall x \in [a, b], f(x) \ge g(x)\)，则 \(\displaystyle \int_a^b f(x) \,{\rm d} x \ge \int_a^b g(x) \,{\rm d} x\)。

3.1.4 微积分基本定理

考虑函数 \(\displaystyle g(x) = \int_a^x f(t) \,{\rm d} t\)，其中 \(x \in [a, b]\)。那么 \(g\) 的几何意义如下图。

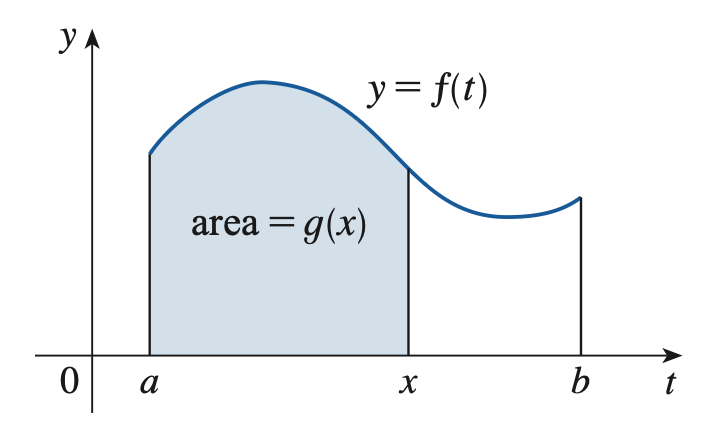
手玩一下，我们会发现在大部分情况中，\(g' = f\)。继续手玩，然后我们就可以明确条件：当 \(f\) 在 \([a, b]\) 上连续时，\(g' = f\)。

证明：使用定义：

\[g'(x) = \lim_{h \to 0} \left( \dfrac{g(x + h) - g(x)}{h} \right) \]

考虑几何意义，\(g(x + h) - g(x)\) 就是下图中的涂色部分，我们把它近似成长方形。

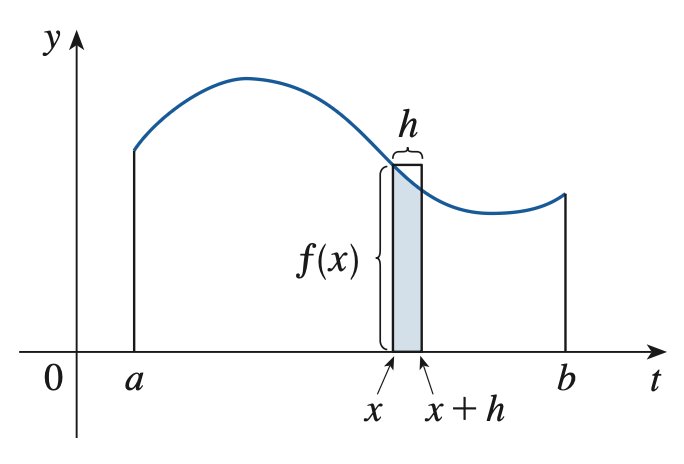
那么 \(\dfrac{g(x + h) - g(x)}{h} = f(x)\)，则 \(g'(x) = \lim \limits_{h \to 0} f(x) = f(x)\)。\(\square\)

从这里我们可以发现，积分对应着前缀和，而微分（求导）对应着差分。实际上有些书会直接写“Discrete Calculus”，因为确实很像。

我们知道，前缀和最典型的用途是求区间和。给定 \(n\) 个数 \(a_1, a_2, \ldots, a_n\)，设 \(S_i = \sum \limits_{j = 1}^i a_i\)，则 \(\sum \limits_{i = l}^r a_i = S_r - S_{l - 1}\)。注意到 \(a\) 是 \(S\) 的差分。

类比一下，我们猜测当 \(f(x)\) 在 \([a, b]\) 上连续时，\(\displaystyle \int_a^b f(x) \,{\rm d} x = F(b) - F(a)\)，其中 \(F' = f\)。

证明：设 \(\displaystyle g(b) = \int_a^b f(x) \,{\rm d} x\)，则 \(g\) 是 \(f\) 的原函数，而 \(F\) 也是 \(f\) 的原函数。则设 \(g(b) = F(b) + C\)。

现在只用解出 \(C\)。使用经典的特殊值法，令 \(b = a\)，则 \(g(a) = F(a) + C\)，解得 \(C = -F(a)\)，则 \(g(b) = F(b) - F(a)\)。\(\square\)

因为 \(F(b) - F(a)\) 这样的式子比较常见，所以数学家们发明了专用的记号：\(F(x) |_a^b = F(b) - F(a)\)。但我基本不用。

把上文的两个结论合到一起，就是微积分基本定理。这个定理阐释了微分与积分互为逆运算的关系，简便了运算，触及了本质。

3.2 不定积分

3.2.1 定义

在 3.1 节中，原函数大量出现，但是我们没有好的符号来指代它。所以数学家们发明了 \(\displaystyle \int f(x) \,{\rm d} x\) 来指代 \(f\) 的原函数。如 \(\displaystyle \int x^2 \,{\rm d} x = \dfrac{x^3}{3} + C\)。

注：有时会省略 \(+C\) 不写。

注意到，求原函数时需要指定区间，所以使用这个记号时，（不）等式一般只在一个区间内成立。

3.2.2 运算法则

1. \(\displaystyle \int c \cdot f(x) \,{\rm d} x = c \int f(x) \,{\rm d} x\)。
2. \(\displaystyle \int (f(x) + g(x)) \,{\rm d} x = \int f(x) \,{\rm d} x + \int g(x) \,{\rm d} x\)。

3.2.3 特殊函数的不定积分

\(f(x)\)	\(\displaystyle \int f(x) \,{\rm d} x\)
\(k\)	\(kx + C\)
\(x^n\)	\(\dfrac{x^{n + 1}}{n + 1} + C\)
\(\sin(x)\)	\(-\cos(x) + C\)
\(\cos(x)\)	\(\sin(x) + C\)
\(e^x\)	\(e^x + C\)
\(1 / x\)	\(\ln(x) + C\)

3.2.4 换元积分法

考虑求 \(I = \displaystyle \int 2x \sqrt{1 + x^2} \,{\rm d} x\)。这看着就不是什么善茬，所以肯定要简化一下式子。

先把根号搞定。令 \(u = 1 + x^2\)，则：

\[I = \int 2x \sqrt{u} \,{\rm d} x \]

注意到 \(2x \,{\rm d} x = {\rm d} u\)，则：

\[I = \int \sqrt{u} \,{\rm d} u = \dfrac{1}{2} u^{3 / 2} = \dfrac{1}{2} \left( 1 + x^2 \right)^{3 / 2} \]

验算可以发现，这是正确的。

---

1. 个人认为这里不太严谨，但本来就是“直观上”，就不深究了。 ↩︎

2. 归纳证明即可。 ↩︎

3. 由 DeepSeek 给出。 ↩︎

4. 具体见此。 ↩︎