电学笔记
由于笔者还没学完,所以这个笔记还不全,缺了不少内容。
记号约定:
- \(\operatorname{norm}(\mathbf{v})\):与 \(\mathbf{v}\) 同向的单位向量,为 \(\dfrac{\mathbf{v}}{|\mathbf{v}|}\)。
1. 电场
1.1 电荷
1.1.1 定义
电荷是物质的一种属性,可以让物质在电场中受力。[1]
注:有争议。
我们规定:
- 正电荷:用丝绸摩擦过的玻璃棒带的电荷。
- 负电荷:用毛皮摩擦过的橡胶棒带的电荷。
有时将带正电荷的粒子简称为正电荷,带负电荷的粒子简称为负电荷。
仿照“质点”的概念,当带电体之间的距离远大于自身的大小,使得带电体的形状、大小和电荷分布状况可以忽略不计时,我们把这样的带电体抽象成一个带电的点,称为点电荷。
1.1.2 电荷量
我们想要衡量物体带电量的多少,那么先把它定义为电荷量,记作 \(Q\) 或 \(q\),单位为库伦(\(\mathrm{C}\))。
定义 \(1 \,\mathrm{C}\) 为 \(1 \,\mathrm{A}\) 电流在 \(1 \,\mathrm{s}\) 传输的电荷量。
注:通过量纲分析,我们可以猜出电流的定义式:\(I = \dfrac{q}{t}\)。
我们发现,\(1 \,\mathrm{C}\) 的数量级还是过于大了。类比化学中的“相对原子质量”,定义元电荷为最小带电体的电荷量,记作 \(e\)。
由化学知识可知,质子的电荷量为 \(+1e\),电子为 \(-1e\)。Robert Andrews Millikan 经过实验测定,\(1e = 1.6 \cdot 10^{-19} \,\mathrm{C}\),获得了 1923 年诺贝尔物理学奖。
注意:\(+1e\) 和 \(-1e\) 的正负号只说明带正电和带负电,不参与比大小。
因为电荷量是整数,所以电荷量一定是 \(e\) 的整数倍。
1.1.3 净电荷量
定义中和为等量异种电荷接触时,都变为不带电的状态的现象。
定义净电荷量为物体内部正负电荷中和后的电荷量。
常说的“带正电”“带负电”指的是净电荷量的正负。当然,“不带电”(“电中性”)不代表物体内部没有电荷。
1.1.4 电荷守恒定律
在封闭的物理系统中,净电荷量不变。
注意:不是电荷的个数不变。
1.1.5 相互作用
电荷间有力的相互作用:同性相斥,异性相吸。
有力就会有运动:正电荷(原子核)不能转移,负电荷(电子)可以转移。
于是,我们可以让原本不带电的物体带电,这个过程叫做起电。
摩擦起电
因为不同原子对电子的束缚能力不同,所以导致电子在物体间转移,让两个物体分别带等量异种电荷。
为什么是“等量异种电荷”?因为电荷守恒定律。
接触起电
两个相同物体接触后,都带等量同种电荷。
注:先中和,再平分。
感应起电
利用静电感应使金属导体带电的过程。
如图,把一个正电荷放到一个导体附近,那么导体内部的负电荷会去到离正电荷近的一端,正电荷去远的一端,那么这个导体离正电荷近的一端会带上负电,远的一端带上正电。
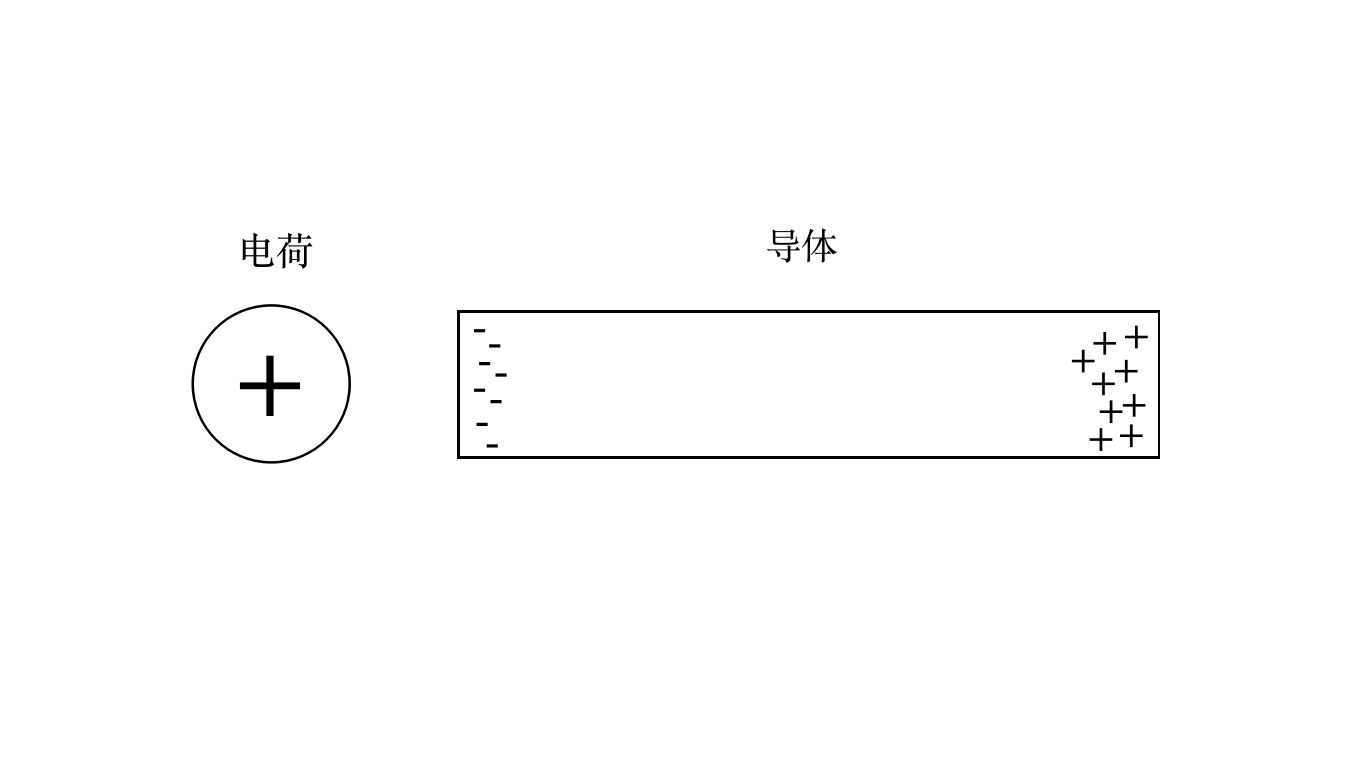
可以总结规律:近端带异种电荷,远端带同种电荷。
如果把那个正电荷撤掉,导体会很快恢复到不带电的状态。
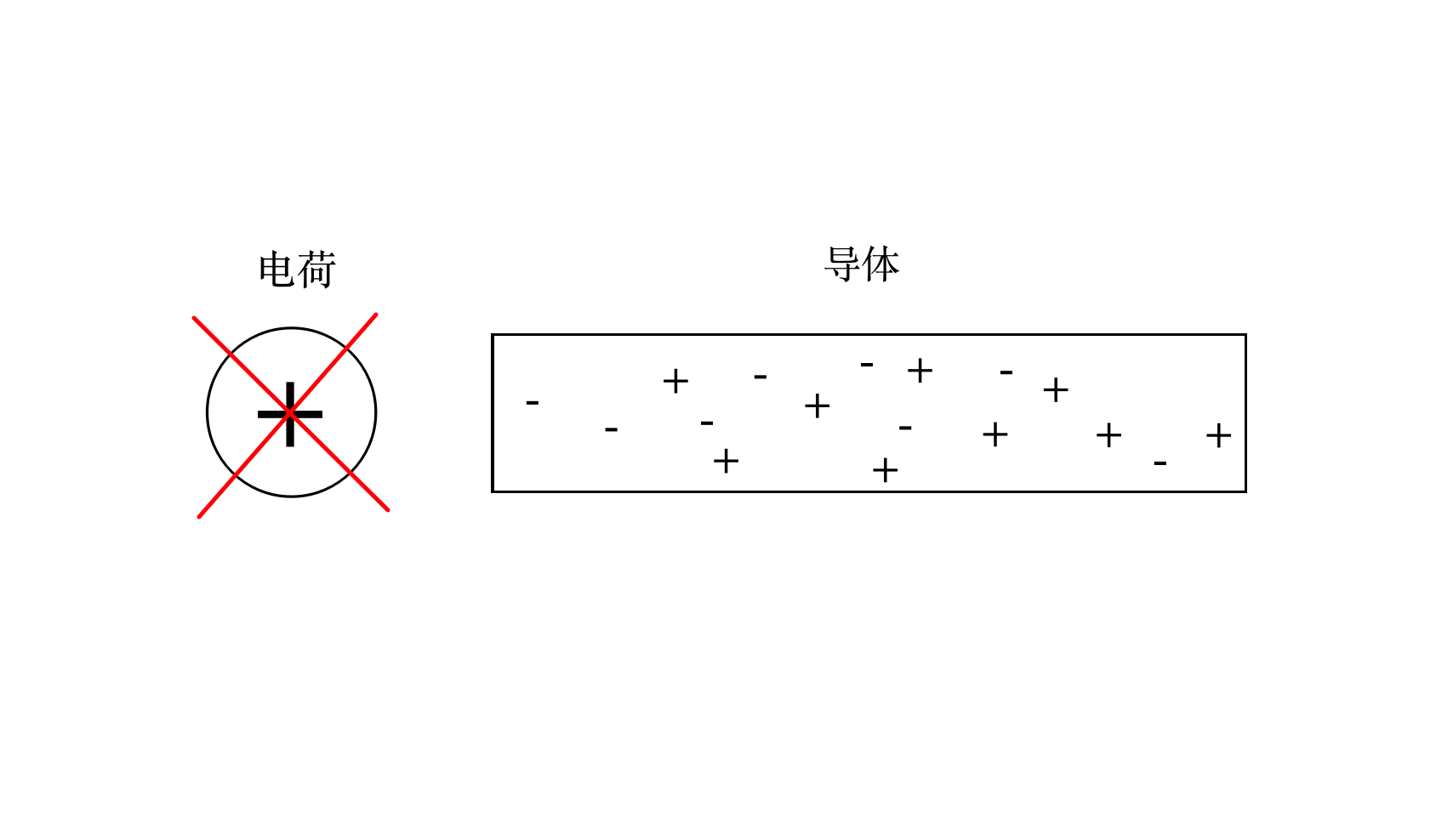
如果把导体劈成两半,再撤掉正电荷,因为导体两端断开,所以正负电荷无法恢复,一半带负电,另一半带正电。
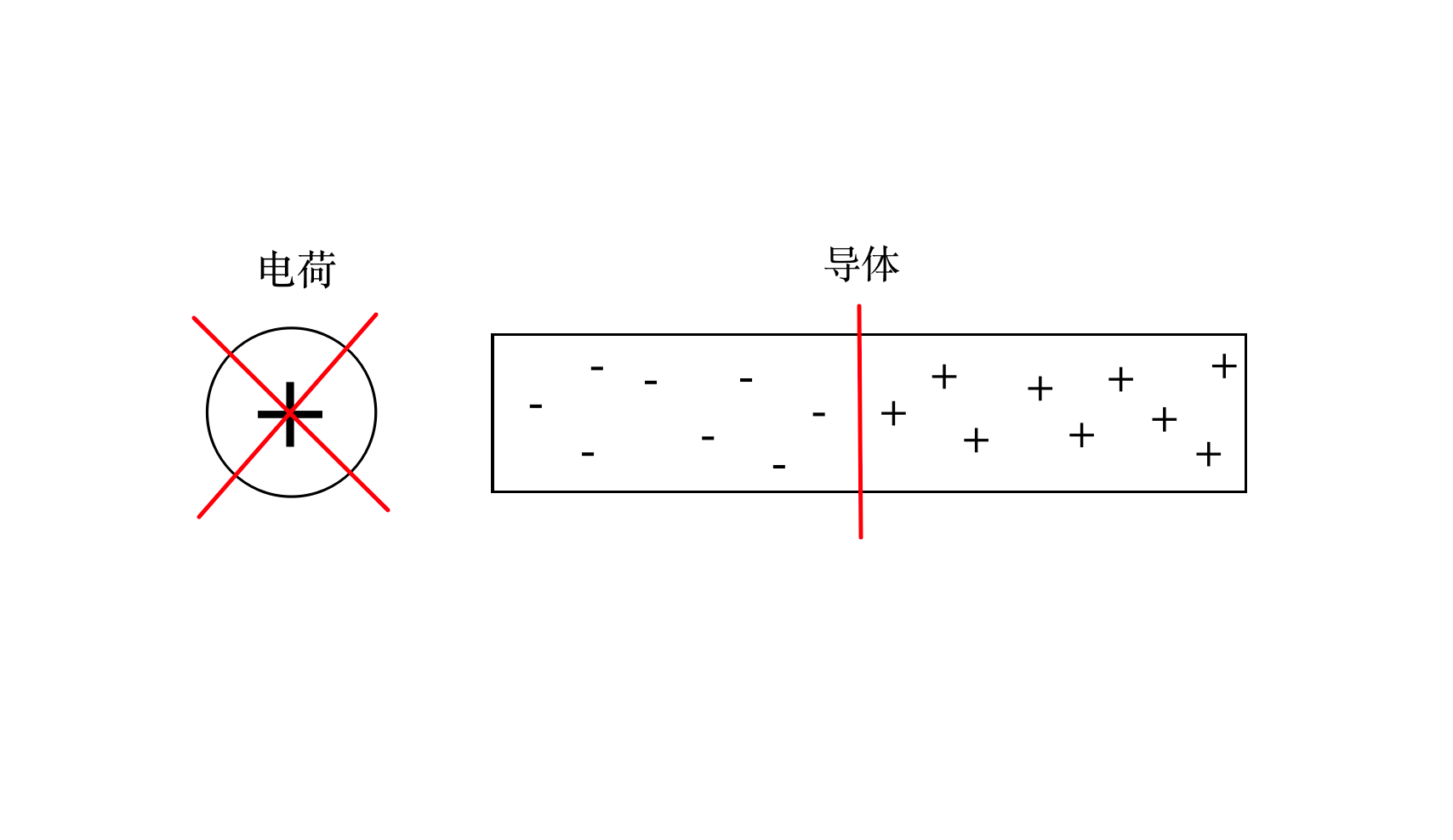
1.1.6 验电器
顾名思义,验电器就是检验物体是否带电的仪器。
用金属杆连接金属球和金属箔。不妨设物体带正电,验电时:
- 让该物体靠近金属球。
- 因为感应起电,金属球会带负电,金属箔带正电。
- 金属箔张开。
1.1.7 库仑力
原来想把这一节并到 1.1.5 中的,但是它太重要了,所以单开一节。
由 1.1.5 节,我们知道电荷间有力,叫做库仑力。
设真空中两个静止点电荷 \(Q_1, Q_2\) 的电荷量分别为 \(q_1, q_2\),\(\operatorname{norm} \left( \overrightarrow{Q_1 Q_2} \right) = \mathbf{e}_{12}\),\(\left| \overrightarrow{Q_1 Q_2} \right| = r\),\(Q_1\) 向 \(Q_2\) 施加的的库仑力为 \(\mathbf{F}_{12}\)。
注:库仑定律仅在两电荷静止、处于真空、且是点电荷时适用。
但是实际做题时没说“视为点电荷”怎么办?若距离大于半径的 \(10\) 倍时,可以用。如果是绝缘且均匀带电的小球,不到 \(10\) 倍也可以用。但是如果是金属球,且球心距不到半径 \(10\) 倍时不能用!
我们知道物体 \(A\) 施加给物体 \(B\) 的引力为
其中 \(\mathbf{e}_{AB} = \operatorname{norm} \left( \overrightarrow{AB} \right)\),\(G\) 为常数,\(m_A, m_B\) 分别为 \(A, B\) 的质量,\(r = \left| \overrightarrow{AB} \right|\)。
那么库仑力是不是类似呢?实际上
其中 \(k = 9 \cdot 10^9 \,\mathrm{N \cdot m^2 \cdot C^{-2}}\)。注意:此处的电荷量带有符号。
容易发现,当 \(q_1, q_2\) 异号时,两者的库伦力指向对方(异性相吸);否则指向对方的反方向(同性相斥)。数值上,\(|\mathbf{F}_{12}| \propto q_1 q_2, |\mathbf{F}_{12}| \propto \dfrac{1}{r^2}\)。
这个公式被称作库仑定律。
1.2 电场
1.2.1 定义
电荷的周围存在着由它产生的电场,形成电场的电荷叫场源。
1.2.2 强度 & 方向
我们发现一个电场内的每一点受到的库仑力都不同。
以引力场举例,把一个物体放到天体的引力场内,然后测定它受的引力,就可以知道该点引力场的强度和方向。
同理,我们可以往一个电场的某一个位置放一个电荷(试探电荷),然后测量它受的库仑力,来衡量该点电场的强度和方向,用 \(\mathbf{E}\) 表示,叫做场强。
那不就是向量场吗?
为了统一标准,我们限定试探电荷必须是 \(+1 \,\mathrm{C}\) 的点电荷。
现在设电荷 \(Q\) 所在位置场强为 \(\mathbf{E}\),且它的电荷量为 \(q\),通过实验可知,它受到的库仑力为 \(\mathbf{F} = q \mathbf{E}\)。那么如果知道 \(\mathbf{F}\) 和 \(q\),就可以知道 \(\mathbf{E} = \dfrac{\mathbf{F}}{q}\)。容易发现,\(|\mathbf{E}|\) 的单位是 \(\mathrm{N / C}\)。
注意:\(\mathbf{E}\) 和 \(\mathbf{F}, q\) 均无关。
那如果有两个电场呢?直接加到一起即可:设电场 \(\mathbf{E}\) 为电场 \(\mathbf{E}_1, \mathbf{E}_2\) 的叠加,则 \(\mathbf{E}(\mathbf{r}) = \mathbf{E}_1(\mathbf{r}) + \mathbf{E_2}(\mathbf{r})\)。
1.2.3 电场线
电场线就是用于描述电场的场强分布的一组带箭头的曲线,在现实中不存在。
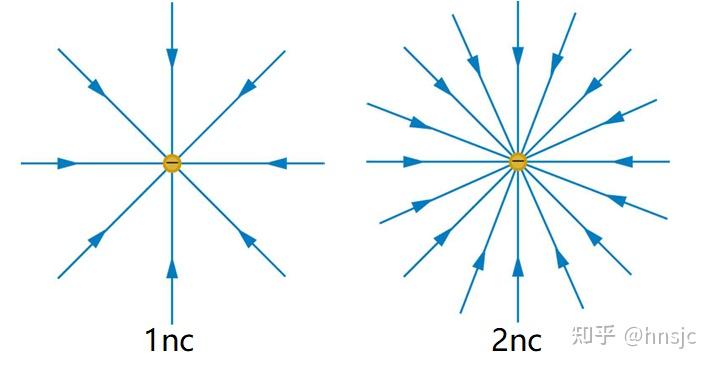
电场线某点的切线方向即为该点场强的方向,疏密程度描述场强大小(越密越强,越疏越弱)。容易发现,同一电场内任意两条电场线一定不相交,因为一个点的场强不能有两个方向。
Q. 那能不能相切呢?
A. 不能,不然这个点的场强大小是 \(+\infty\),显然矛盾。
注意:电场线不是带电粒子在电场中的移动轨迹。如果真的想算速度,需要把原来的速度向量加上加速度,不能认为是力的方向。
1.2.4 点电荷电场
顾名思义,点电荷电场就是场源是点电荷的电场。
把 \(\mathbf{E} = \dfrac{\mathbf{F}}{q}\) 代入库仑定律,可得:
其中 \(q\) 是场源的电荷量。
1.2.5 匀强电场
顾名思义,定义场强处处相等的电场为匀强电场。
这听着就很难实现,但实际上很好办,只需把两块分别带正电和负电的金属板摆成下图即可。
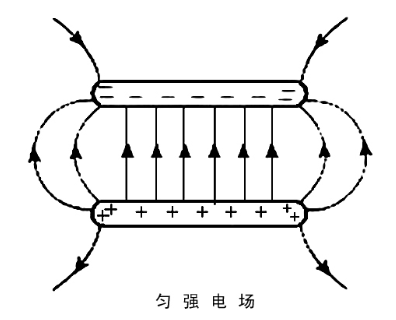
他们之间的部分可以近似成匀强电场。
2. 恒定电流
2.1 电流
2.1.1 定义
导体中的自由电荷定向移动形成电流。注意:没有电流不代表电荷静止。
2.1.2 大小
电流的大小被称作电流强度,简称电流,记作 \(I\)。
我们定义:
其中 \(q\) 是 \(t\) 单位时间内通过导体横截面的电荷量。当然,令 \(t \to 0\),就得到了瞬时电流。
接下来分析量纲,\(q\) 的单位是库伦(\(\mathrm{C}\)),\(t\) 的单位是秒(\(\mathrm{s}\)),那么 \(I\) 的单位是 \(\mathrm{C / s}\),叫做安培,简称安,记作 \(\mathrm{A}\)。它的变种有 \(1 \,\mathrm{mA} = 10^{-3} \,\mathrm{A}\)、\(1 \,\mathrm{\mu A} = 10^{-6} \,\mathrm{A}\)。
2.1.3 方向
回到定义,电流是电荷定向移动,那么电流一定有方向。我们定义电流的方向为正电荷定向移动的方向。如果实际移动的是负电荷(电子),有时会不易分析,所以等效成正电荷向反方向移动。
那么它是向量吗?不是,因为它不满足向量运算法则。
注意:判断一个事物是不是向量的唯一方法是:判断它满不满足向量运算法则,满足就是,不满足就不是。
2.1.4 存在条件
- 电路形成闭合回路。
- 导体两端存在电势差。
2.2 电阻
2.2.1 定义
导体对电流的阻碍作用叫电阻。
2.2.2 欧姆定律
记电阻的大小为 \(R\),单位为欧姆,简称欧,记作 \(\Omega\)。
欧姆定律:
其中 \(U\) 是电压,\(I\) 是电流。注意:\(R\) 与 \(U, I\) 无关,是导体自身的属性。
Q. 做实验时加大电压,可以观察到电阻升高。那么 \(R\) 为何还和 \(U\) 无关?
A. 加大电压会让导体发热,温度升高影响了电阻。
2.2.3 串联电路
将 \(R_1, R_2, \ldots, R_n\) 串联在一起,则这个电路的 \(U = \sum \limits_{i = 1}^n U_i\),且 \(I\) 恒定。
代入 \(U = IR\),得 \(IR = \sum \limits_{i = 1}^n IR_i\),即 \(R = \sum \limits_{i = 1}^n R_i\)。
2.2.4 并联电路
将 \(R_1, R_2, \ldots, R_n\) 并联在一起,则这个电路的 \(I = \sum \limits_{i = 1}^n I_i\),且 \(U\) 恒定。
代入 \(I = \dfrac{U}{R}\),得 \(\dfrac{U}{R} = \sum \limits_{i = 1}^n \dfrac{U}{R_i}\),即 \(\dfrac{1}{R} = \sum \limits_{i = 1}^n \dfrac{1}{R_i}\)。
3. 电学实验
3.1 多用电表
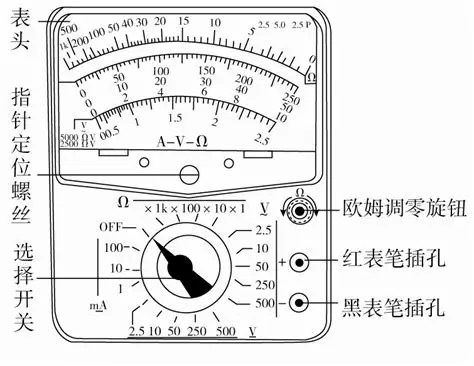
3.1.1 测电阻
原理
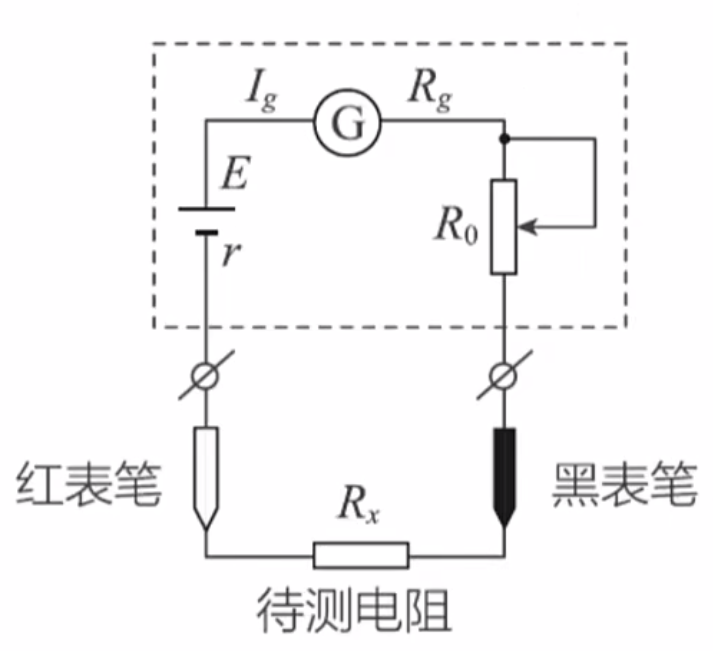
(虚框是电表内部,\(\mathrm{G}\) 为灵敏电流表。)
把两个表笔分别接到待测电阻的两端,则会形成上图的电路。电路的总电阻为 \(R_x + R_{\text{int}}\),其中
\(R_{\text{int}}\) 是电表内部的所有电阻,在上图中为 \(R_g + R_0\)。于是由欧姆定律:
解得
观察多用电表中 \(\Omega\) 一行的示数,发现相邻示数间距不同。是因为 \(R_x\) 与 \(I_g\) 成反比(其实差一个常数)。
考虑一些特殊值。如果 \(I_g = 0\),那么我们希望此时 \(R_x \to +\infty\),这与实际计算是吻合的。如果 \(I_g\) 满量程,那么我们希望此时 \(R_x = 0\),所以应有
发现等式中只有 \(R_0\) 能变,所以需要让 \(R_0 = \dfrac{E}{I_g} - R_g\),才能符合实际。这不是定值吗?为啥要用滑动变阻器?因为定值电阻的电阻会随时间推移而变化,把它换成滑动变阻器就可以解决问题。实际上,多用电表上的欧姆调零旋钮就是用来干这件事的。
如何在不知道 \(E\) 和 \(I_g\) 时算出 \(R_{\text{int}}\)?继续用特殊值法。找到表头满偏和半偏对应的 \(R_x\),则有
解得
可以二分 \(R_x\),精度只受工艺和成本限制。称可以让表头半偏的电阻为中值电阻。实际使用时当然不用二分,一般可以直接在表上读出中值电阻。
Wikipedia contributors, "Electric charge," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Electric_charge&oldid=1296440770 (accessed August 5, 2025). ↩︎



 浙公网安备 33010602011771号
浙公网安备 33010602011771号