做题记录（MO）

代数篇
几何篇
函数篇
数论篇
组合数学篇
神秘题目

记号约定：

$\mathbb{P}$：全体质数集合。
$a \perp b$：直线 $a$ 与 $b$ 垂直；整数 $a$ 和 $b$ 互质。
$a \parallel b$：直线 $a$ 与 $b$ 平行；（规定 $\exist i \in \N, p \in \mathbb{P}, a = p^i$）整数 $p^i, b$ 满足 $p^i \mid b, p^{i + 1} \nmid b$。
$\nu_p(n)$：质数 $p$ 在整数 $n$ 的质因数分解中的幂次。
$[x^n] f(x)$：多项式 $f(x)$ 中 $x^n$ 的系数。
（Iverson 括号）$[\mathrm{P}]$：命题 $\mathrm{P}$ 为真时取 $1$，否则取 $0$。

更新记录：

2025.8.11。

代数篇

1. 因式分解：$2x^5+7x^4+12x^3+14x^2+10x+3$。

正解（试根法）：我们可以先试出一个根 $x=-1$，从而得到因式 $x-(-1)=x+1$。

\[\begin{aligned} &2x^5+7x^4+12x^3+14x^2+10x+3 \\ = \ &(x+1)(2x^4+5x^3+7x^2+7x+3) \\ = \ &(x+1)^2(2x^3+3x^2+4x+3) \\ = \ &(x+1)^3(2x^2+x+3) \end{aligned} \]
$2x^2+x+3$ 不可被分解，因为其判别式 $b^2-4ac=1^2-4 \times 2 \times 3 = -23 < 0$。

2. $x^5-5qx+4r$ 可以被 $(x-c)^2$ 整除，其中 $c$ 为常数。求 $q$ 与 $r$ 的关系。

正解（待定系数法）：设 $x^5-5qx+4r=(x^2-2cx+c^2)(x^3+mx^2+nx+\dfrac{4r}{c^2})$。

则其三次项为 $(n-2cm+c^2)x^3=0$，其四次项为 $(m-2c)x^4=0$，则 $m=2c,n=3c^2$。

此时二次项为 $(\dfrac{4r}{c^2}-4c^3)x^2=0$，一次项为 $(-\dfrac{8r}{c}+3c^4)x=-5qx$。故 $q=c^4,r=c^5 \implies q^5=r^4$（关系中不应出现 $c$）。

3. 已知 $a+b+c=1,b^2+c^2-4ac+6c+1=0$，求 $abc$ 的值。

正解（配方法）：尝试代入 $b=1-a-c$，则 $b^2+c^2-4ac+6c+1=a^2+2c^2-2ac-2a+4c+2$，我们对这个式子束手无策。

故尝试代入 $a=1-b-c$，则 $b^2+c^2-4ac+6c+1=b^2+c^2+2c+4bc+4c^2+1=(b+2c)^2+(c+1)^2=0$。（技巧：优先代入次数少的字母。）

故 $b+2c=c+1=0 \implies b=2,c=-1 \implies a=0$，则 $abc=0$。

评注：在遇到一个值可以变为 0 的二次式时，可以想办法配方。

4. 已知 $14(a^2+b^2+c^2)=(a+2b+3c)^2$，求 $a:b:c$。

正解（配方法）：先暴力拆括号：$14a^2+14b^2+14c^2=a^2+4b^2+9c^2+4ab+12bc+6ac$，则 $13a^2+10b^2+5c^2-4ab-12bc-6ac=0$。

将 $13a^2$ 拆为 $4a^2+9a^2$，$10b^2$ 拆为 $b^2+9b^2$，$5c^2$ 拆为 $c^2+4c^2$。

则 $(2a-b)^2+(3b-2c)^2=0 \implies b=2a,2c=3b \implies a:b=1:2,b:c=2:3 \implies a:b:c=1:2:3$。

5. 证明 $2^{2023}+1$ 不为素数，并分别写出它们的一个真因数（即不为 1 和其本身的正因数）。

证明：$2^{2023}+1=(2+1)(2^{2022}-2^{2021}+2^{2020}-\cdots-2+1)$（此处使用公式：$x^n+y^n=(x+y)(x^{n-1}-x^{n-2}y+x^{n-3}y^2-\cdots-xy^{n-2}+y^{n-1})$，其中 $n$ 为奇数），则 $2+1=3$ 整除 $2^{2023}+1$，故其不为素数。

5.1. 证明 $2^{2024}+1$ 不为素数，并分别写出它们的一个真因数。

证明：

\[\begin{aligned} &2^{2024}+1 \\ = \ &(2^{88})^{23}+1^{23} \\ = \ &(2^{88}+1)(2^{88 \times 22}-2^{88 \times 21}+2^{88 \times 20}-\cdots-2^{88 \times 1}+1) \end{aligned} \]
则 $2^{88}+1$ 整除 $2^{2024}+1$，故其不为素数。

6. 因式分解：$6x^2-6y^2+5xy+2yz-3xz-2x-3y+z$。

正解（主元法）：设 $z$ 为主元，则

\[\begin{aligned} &6x^2-6y^2+5xy+2yz-3xz-2x-3y+z \\ = \ &(2y-3z+1)z+(6x^2-6y^2+5xy-2x-3y) \\ = \ &(2y-3z+1)z+(2x+3y)(2y-3x+1) \\ = \ &(2y-3x+1)(z-2x-3y) \end{aligned} \]
当然，设 $x$ 或 $y$ 为主元也是可以的。

7. 解方程：$|5x+2|=|2x+3|$。

思路：我们发现 $|A|=|B| \implies A=\pm B$。据此分类讨论即可。

正解：

若 $5x+2=2x+3$：则 $3x=1 \implies x=\dfrac{1}{3}$。

若 $5x+2=-(2x+3)$：则 $7x+5=0 \implies 7x=-5 \implies x=-\dfrac{5}{7}$。

7.1. 解方程：$|5x+2|=2x+3$。

正解：

若 $5x+2 \lt 0$：则 $-(5x+2)=2x+3 \implies x=-\dfrac{5}{7}$。

若 $5x+2 \geq 0$：则 $5x+2=2x+3 \implies x=\dfrac{1}{3}$。

评注：虽然此题的解与上题的一致，但不可使用上题的方法，因为上题的方法在此题不保证 $2x+3 \geq 0$。所以我们只能化简绝对值。

8. 解五元方程组：

\[\begin{cases} x_1-x_2+x_3=1 \\ x_2-x_3+x_4=2 \\ x_3-x_4+x_5=3 \\ x_4-x_5+x_1=4 \\ x_5-x_1+x_2=5 \end{cases} \]

正解（高斯消元法）：将方程组写成矩阵形式：

\[\left( \begin{matrix} 1 & -1 & 1 & 0 & 0 & 1 \\ 0 & 1 & -1 & 1 & 0 & 2 \\ 0 & 0 & 1 & -1 & 1 & 3 \\ 1 & 0 & 0 & 1 & -1 & 4 \\ -1 & 1 & 0 & 0 & 1 & 5 \end{matrix} \right) \]
其中每一行表示这五个未知数分别的系数与等号右边的值（比如第一行表示 $1x_1+(-1)x_2+1x_3+0x_4+0x_5=1$）。忽略最后一列，我们的目标是：将主对角线以下的数全部变成 0。

我们可以使用以下操作，因为它们不改变方程组的解：

将两行交换。

将一行同时乘以 $m$。

将一行同时加上 $n$。

矩阵最终变为：

\[\left( \begin{matrix} 1 & -1 & 1 & 0 & 0 & 1 \\ 0 & 1 & -1 & 1 & 0 & 2 \\ 0 & 0 & 1 & -1 & 1 & 3 \\ 0 & 0 & 0 & -1 & 1 & -4 \\ 0 & 0 & 0 & 0 & -1 & 1 \end{matrix} \right) \]
还原到方程组，得：

\[\begin{cases} x_1-x_2+x_3=1 \\ x_2-x_3+x_4=2 \\ x_3-x_4+x_5=3 \\ -x_4+x_5=-4 \\ -x_5=1 \end{cases} \]
解得：

\[\begin{cases} x_1=0 \\ x_2=6 \\ x_3=7 \\ x_4=3 \\ x_5=-1 \end{cases} \]

9. 解不等式：$\dfrac{2}{x}<6$。

解法 1：两边同时乘 $x$。分类讨论 $x$ 的符号：

若 $x>0$：则 $2<6x \implies x>\frac{1}{3}$。

若 $x<0$：则 $2>6x \implies x<\frac{1}{3}$（此处要取条件 $x<0$ 与结论 $x<\frac{1}{3}$ 的交集 $x<0$）。

则 $x > \dfrac{1}{3}$ 或 $x<0$。

解法 2：两边同时乘 $x^2$，得 $2x<6x^2 \implies 0<6x^2-2x=2x(3x-1) \implies x(3x-1)>0$，则 $x > \dfrac{1}{3}$ 或 $x<0$。

解法 3：由原式可得 $\dfrac{2}{x}-6<0 \implies \dfrac{2-6x}{x}<0 \implies \dfrac{3x-1}{x}>0$，则 $x > \dfrac{1}{3}$ 或 $x<0$。

评注：解法 1 比较麻烦，不建议使用。解法 2 出自高中的课本，但是在一些题中不好用。解法 3 则比较通用，非常推荐。

10. 已知非零实数 $a,b,c,x,y,z$ 满足

\[x^2+y^2+z^2=a^2+b^2+c^2=ax+by+cz \]

求证：$\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}$。

证明（配方）：设 $x^2+y^2+z^2=a^2+b^2+c^2=ax+by+cz=k$。则

\[\begin{aligned} &k+k-2k \\ =\ &x^2+y^2+z^2+a^2+b^2+c^2-2ax+2by+2cz \\ =\ &(a^2-2ax+x^2)+(b^2-2by+y^2)+(c^2-2cz+z^2) \\ =\ &(a-x)^2+(b-y)^2+(c-z)^2 \\ =\ &0 \end{aligned} \]
这说明 $a=x,b=y,c=z \implies \dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=1$，即为原命题。

11. 求 $S_n=\sum_{j=1}^n j^2$。

正解：首先，因为 $p^2=\sum_{q=1}^p (2q-1)$，所以

\[\begin{aligned} S_n &=\sum_{p=1}^n \sum_{q=1}^p (2q-1) \\ &=\sum_{1 \le q \le p \le n} (2q-1) \\ &=2 \sum_{1 \le q \le p \le n} q - \sum_{1 \le q \le p \le n} 1 \end{aligned} \]
现在，我们发现上式的第一项并不好求。我们展开一下：

\[\begin{aligned} \sum_{1 \le q \le p \le n} q=1+(1+2)+(1+2+3)+\cdots+(1+2+3+\cdots+n) \end{aligned} \]
可以发现，展开后有 $1+2+\cdots+n=\dfrac{n(n+1)}{2}$ 项，且 $1$ 被加了 $n$ 次，$2$ 被加了 $(n-1)$ 次······所以，$a$（$1 \le a \le n$）被加了 $(n-a+1)$ 次。所以

\[\begin{aligned} \sum_{1 \le q \le p \le n} q&=\sum_{p=1}^n p(n-p+1) \\ &=n \sum_{p=1}^n p - \sum_{p=1}^n p^2 + \sum_{p=1}^n p \\ &=(n+1) \sum_{p=1}^n p - S_n \\ &=\frac{n(n+1)^2}{2} - S_n \end{aligned} \]
则

\[\begin{aligned} S_n&=2 \sum_{1 \le q \le p \le n} q - \sum_{1 \le q \le p \le n} 1 \\ &=n(n+1)^2-2S_n-\frac{n(n+1)}{2} \\ &=\frac{2n(n+1)^2-n(n+1)}{2}-2S_n \\ &=\frac{n(n+1)(2(n+1)-1)}{2}-2S_n \\ &=\frac{n(n+1)(2n+1)}{2}-2S_n \end{aligned} \]
则 $3S_n=\dfrac{n(n+1)(2n+1)}{2}$，$S_n=\dfrac{n(n+1)(2n+1)}{6}$。

11.1. 求 $S_n = \sum_{j = 1}^n j^3$。

正解：对其求导，得

\[\begin{aligned} S'_n &= 3 \sum_{j = 1}^n j^2 \\ &= \dfrac{n(n + 1)(2n + 1)}{2} \\ &= n^3 + \dfrac{3}{2} n^2 + \dfrac{1}{2} n \end{aligned} \]
则

\[\begin{aligned} S_n &= \int S'_n \,\mathrm dn \\ &= \int (n^3 + \dfrac{3}{2} n^2 + \dfrac{1}{2} n) \,\mathrm{d}n \\ &= \dfrac{1}{4} n^4 + \dfrac{1}{2} n^3 + \dfrac{1}{4} n^2 \\ &= \dfrac{n^2}{4} (n^2 + 2n + 1) \\ &= \dfrac{n^2 (n + 1)^2}{4} \end{aligned} \]

12. 解不等式：$|2-3x|+|2x-1|-|4x-3|<10$。

解法 1（换元法）：这个式子看着就不好看，所以我们令 $u=x-1$。则 $|2u+1|+|3u+1|-|4u+1|<10$。

若 $u \ge 0$：此时 $(2u+1)+(3u+1)-(4u+1)<10 \implies u+1<10 \implies u<9$。

若 $u < -\dfrac{1}{2}$：此时 $-(2u+1)-(3u+1)+(4u+1)<10 \implies -u-1<10 \implies u>-11$。

其它情况不用考虑，一定落在 $(-11,9)$ 的区间内。故 $-11<x<9$。

解法 2（函数）：我们令 $f(x)=|2-3x|+|2x-1|-|4x-3|-10$。先找它的根，为 $x_1=-10,x_2=10$。

零点定理：对于连续函数 $f(x)$，若存在 $a,b$，使得 $f(a) \cdot f(b)<0$，则必有至少一个根在区间 $(a,b)$ 内。

证明：不妨设 $f(a)>0>f(b)$（$f(a)<0<f(b)$ 时证明是相似的），则根据介值定理，$f(x)$ 的图像一定经过 $x$ 轴，则必有至少一个 $m$，使得 $a<m<b$ 且 $f(m)=0$。

令 $a=-10^8,b=0,c=10^8$。

根据零点定理，因为 $f(a)>0>f(b)$，所以在区间 $(x_1,b]$ 即 $(-10,0]$ 上，$f(x)<0$；因为 $f(b)<0<f(c)$，所以在区间 $[b,x_2)$ 即 $[0,10)$ 上，$f(x)<0$。综合起来，就是在区间 $(-10,10)$ 上，$f(x)<0$。

则原题的解为 $-10<x<10$。

13. 已知 $\dfrac{ab}{a+b}=\dfrac{1}{3},\dfrac{bc}{b+c}=\dfrac{1}{4},\dfrac{ca}{c+a}=\dfrac{1}{5}$，求 $\dfrac{abc}{ab+bc+ca}$ 的值。

正解：考虑将条件的分子、分母倒过来（技巧：分子是单项式的分式，我们常求其倒数），即

\[\begin{cases} \frac{a+b}{ab}=3 \\ \frac{b+c}{bc}=4 \\ \frac{c+a}{ca}=5 \end{cases} \]
此时可以使用公式 $\dfrac{a+b}{ab}=\dfrac{1}{a}+\dfrac{1}{b}$ 将等号左边全部拆开，得

\[\begin{cases} \frac{1}{a}+\frac{1}{b}=3 \\ \frac{1}{b}+\frac{1}{c}=4 \\ \frac{1}{c}+\frac{1}{a}=5 \end{cases} \]
将三式相加，得 $\dfrac{2}{a}+\dfrac{2}{b}+\dfrac{2}{c}=12$，即 $\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=6$。

此时

\[\begin{aligned} \dfrac{abc}{ab+bc+ca} &=\dfrac{1}{\frac{ab+bc+ca}{abc}} \\ &=\dfrac{1}{\frac{1}{c}+\frac{1}{a}+\frac{1}{b}} \\ &=\dfrac{1}{6} \end{aligned} \]

14. 化简：

\[\dfrac{(y-x)(z-x)}{(x-2y+z)(x+y-2z)}+\dfrac{(z-y)(x-y)}{(x+y-2z)(y+z-2x)}+\dfrac{(x-z)(y-z)}{(y+z-2x)(x-2y+z)} \]

正解（换元法）：我们发现，$x-y,y-z,z-x$ 三式经常出现，故考虑换元。（技巧：在遇到多次出现的式子时，可以换元以简化式子。）

设 $x-y=A,y-z=B,z-x=C$，则原式为

\[\begin{aligned} &-\dfrac{AC}{(A-B)(B-C)}-\dfrac{BA}{(B-C)(C-A)}-\dfrac{CB}{(C-A)(A-B)} \\ =& -\sum_{\text{cyc}(A,B,C)} \dfrac{AC}{(A-B)(B-C)} \\ =& -\sum_{\text{cyc}(A,B,C)} \dfrac{AC(C-A)}{(A-B)(B-C)(C-A)} \\ =& -\dfrac{\sum_{\text{cyc}(A,B,C)} AC(C-A)}{(A-B)(B-C)(C-A)} \\ =& -\dfrac{AC(C-A)+BA(A-B)+CB(B-C)}{(A-B)(B-C)(C-A)} \\ =& \ \dfrac{(A-B)(B-C)(C-A)}{(A-B)(B-C)(C-A)} \\ =& \ 1 \end{aligned} \]

评注：有时，我们可以适量的使用符号（此题使用了求和号）简化式子，从而发现一些性质。

15. 若 $\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1,\dfrac{a}{x}+\dfrac{b}{y}+\dfrac{c}{z}=0$，求 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}$ 的值。

正解（换元法）：我们发现 $\dfrac{x}{a},\dfrac{y}{b},\dfrac{z}{c}$ 多次出现，故考虑换元。

设 $\dfrac{x}{a}=A,\dfrac{y}{b}=B,\dfrac{z}{c}=C$，则 $A+B+C=1,\dfrac{1}{A}+\dfrac{1}{B}+\dfrac{1}{C}=0$。此时发现换元后仍有分式，故可以让等号两边同乘 $ABC$，消去分母，同时让式子整齐。则

\[\begin{cases} A+B+C=1 \\ AB+BC+CA=0 \end{cases} \]
则

\[\begin{cases} A^2+B^2+C^2+2(AB+BC+CA)=1 \\ AB+BC+CA=0 \end{cases} \]
则 $A^2 + B^2 + C^2 = 1 \implies \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1$

评注：为何不换元 $\dfrac{a}{x},\dfrac{b}{y},\dfrac{c}{z}$？因为它们的和为 0，而用上述方法可以让这个式子提供的信息更多，而且用上述方法求答案更方便，没有分式。

16. 若 $abc = 1$，求 $\sum \limits_{\text{cyc}} \dfrac{1}{1+a+ab}$ 的值。

正解（消元法）：根据条件可得 $c = \dfrac{1}{ab}$。故原式为

\[\begin{aligned} &\dfrac{1}{1+a+ab}+\dfrac{1}{1+b+bc}+\dfrac{1}{1+c+ac} \\ =\ &\dfrac{1}{1+a+ab}+\dfrac{1}{1+b+\dfrac{1}{a}}+\dfrac{1}{1+\dfrac{1}{ab}+\dfrac{1}{b}} \\ =\ &\dfrac{1}{1+a+ab}+\dfrac{a}{a+ab+1}+\dfrac{ab}{ab+1+a} \\ =\ &1 \end{aligned} \]

17. 若 $\dfrac{x}{y+z}+\dfrac{y}{x+z}+\dfrac{z}{x+y}=1$，求 $\dfrac{x^2}{y+z}+\dfrac{y^2}{x+z}+\dfrac{z^2}{x+y}$ 的值。

正解：则

\[\begin{aligned} &\dfrac{x(x+y+z)}{y+z}+\dfrac{y(x+y+z)}{x+z}+\dfrac{z(x+y+z)}{x+y} \\ =\ &\sum_{\text{cyc}} \dfrac{x^2+x(y+z)}{y+z} \\ =\ &\sum_{\text{cyc}} \dfrac{x^2}{y+z}+(x+y+z) \\ =\ &x+y+z \end{aligned} \]
故原式为 $0$。

17. 若 $\dfrac{x}{y+z+u}=\dfrac{y}{x+z+u}=\dfrac{z}{x+y+u}=\dfrac{u}{x+y+z}$，求 $\dfrac{x+y}{z+u}+\dfrac{y+z}{x+u}+\dfrac{z+u}{x+y}+\dfrac{x+u}{y+z}$ 的值。

正解：首先介绍一个公式：$\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d} \quad (b+d \neq 0)$。

证明：

\[\begin{aligned} &\dfrac{a}{b}=\dfrac{c}{d} \\ \implies\ &ad=bc \\ \implies\ &\dfrac{ad}{b}=c \\ \implies\ &a+\dfrac{ad}{b}=a+c \\ \implies\ &\dfrac{a(b+d)}{b}=a+c \\ \implies\ &\dfrac{a}{b}=\dfrac{a+c}{b+d} \\ \implies\ &\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d} \end{aligned} \]
故原命题得证。

则 $\dfrac{x}{y+z+u}=\dfrac{y}{x+z+u}=\dfrac{z}{x+y+u}=\dfrac{u}{x+y+z}=\dfrac{x+y+z+u}{3(x+y+z+u)}=\dfrac{1}{3}$。

则

\[\begin{cases} 3x=y+z+u \\ 3y=z+u+x \\ 3z=u+x+y \\ 3u=x+y+z \end{cases} \]
则 $u=\dfrac{x+y+z}{3}$。将其代入得

\[\begin{cases} 3x=y+z+\dfrac{x+y+z}{3} \\ 3y=x+z+\dfrac{x+y+z}{3} \\ 3z=x+y+\dfrac{x+y+z}{3} \end{cases} \]
则

\[\begin{cases} 2x=y+z \\ 2y=z+x \\ 2z=x+y \end{cases} \]
即 $x=y=z$，则 $x=y=z=u$。故原式 $=4$。

18. 已知 $a, b, c$ 为非零有理数，满足 $ab^2 = \dfrac{c}{a} - b$，求

\[\left( \dfrac{a^2 b^2}{c^2} - \dfrac{2}{c} + \dfrac{1}{a^2 b^2} + \dfrac{2ab}{c^2} - \dfrac{2}{abc} \right) \div \left( \dfrac{2}{ab} - \dfrac{2ab}{c} \right) \div \dfrac{101}{c} \]

的值。

正解：首先观察，我们可以发现 $\dfrac{a^2 b^2}{c^2} - \dfrac{2}{c} + \dfrac{1}{a^2 b^2}$ 可以配方成 $\left( \dfrac{ab}{c} - \dfrac{1}{ab} \right)^2$。同时，

\[\begin{aligned} \left( \dfrac{2}{ab} - \dfrac{2ab}{c} \right) \cdot \dfrac{101}{c} &= \dfrac{2c - 2a^2 b^2}{abc} \cdot \dfrac{101}{c} \\ &= \dfrac{202(c - a^2 b^2)}{abc^2} \\ &= \dfrac{202(c - c + ab)}{abc^2} \\ &= \dfrac{202}{c^2} \end{aligned} \]
故原式为

\[\begin{aligned} \left( \left( \dfrac{ab}{c} - \dfrac{1}{ab} \right)^2 + \dfrac{2ab}{c^2} - \dfrac{2}{abc} \right) \div \dfrac{202}{c^2} &= \left( -\dfrac{1}{c^2} - \dfrac{2}{c^2} \right) \div \dfrac{202}{c^2} \\ &= -\dfrac{3}{c^2} \cdot \dfrac{c^2}{202} \\ &= -\dfrac{3}{202} \end{aligned} \]

19. 解下列方程组：

\[\begin{cases} \frac{1}{x} + \frac{1}{y + z} = \frac{1}{2} \\ \frac{1}{y} + \frac{1}{z + x} = \frac{1}{3} \\ \frac{1}{z} + \frac{1}{x + y} = \frac{1}{4} \end{cases} \]

正解：先通分：

\[\begin{cases} \dfrac{x + y + z}{x(y + z)} = \dfrac{1}{2} \\ \dfrac{x + y + z}{y(z + x)} = \dfrac{1}{3} \\ \dfrac{x + y + z}{z(x + y)} = \dfrac{1}{4} \end{cases} \]
去分母得：

\[\begin{cases} 2(x + y + z) = xy + xz \\ 3(x + y + z) = xy + yz \\ 4(x + y + z) = xz + yz \end{cases} \]
三式相加得 $9(x + y + z) = 2(xy + yz + zx)$。即 $4.5(x + y + z) = xy + yz + zx$。

则

\[\begin{cases} yz = 2.5(x + y + z) \\ xz = 1.5(x + y + z) \\ xy = 0.5(x + y + z) \end{cases} \]
则

\[\begin{cases} y : x = 5 : 3 \\ z : y = 3 : 1 \end{cases} \]
则 $x : y : z = 3 : 5 : 15$。设 $x = 3k, y = 5k, z = 15k$。原方程组变为

\[\begin{cases} \frac{1}{3k} + \frac{1}{20k} = \frac{1}{2} \\ \frac{1}{5k} + \frac{1}{18k} = \frac{1}{3} \\ \frac{1}{15k} + \frac{1}{8k} = \frac{1}{4} \end{cases} \]
解得 $k = \dfrac{23}{30}$。则

\[\begin{cases} x = 2.3 \\ y = \dfrac{23}{6} \\ z = 11.5 \end{cases} \]

20. 设关于 $x$ 的二次方程 $(k^2 - 6k + 8)x^2 + (2k^2 - 6k - 4)x + k^2 = 4$ 的两个根都是整数，求所有满足条件的实数 $k$ 的值。

正解：将原方程变形：

\[\Big((k - 2)x + (k + 2) \Big) \Big((k - 4)x + (k - 2) \Big) = 0 \]
则 $x_1 = -\dfrac{k + 2}{k - 2} = -1 - \dfrac{4}{k - 2}, x_2 = -\dfrac{k - 2}{k - 4} = -\left(1 + \dfrac{2}{k - 4} \right) = -1 - \dfrac{2}{k - 4}$。

这说明 $4 \mid k - 2, 2 \mid k - 4$。此时 $k - 2 \in \{1, 4, -1, -4 \}, k - 4 \in \{1, 2, -1, -2 \}$，即 $k \in \{3, 6, 1, -2 \}, k \in \{5, 6, 3, 2 \}$。则 $k \in \{3, 6 \}$。

21. 设 $a, b, c$ 均为整数，且 $a^2 + b^2 + c^2 + 3 < ab + 3b + 2c$，写一个以 $a + b, c - b$ 为根的一元二次方程。

正解（配方）：发现常数 $3$ 很不顺眼，但是把它改成 $4$ 就可以配方。故

\[\left(a - \dfrac{1}{2}b \right)^2 + \left(\dfrac{\sqrt{3}}{2}b - \sqrt{3} \right)^2 + (c - 1)^2 < 1 \]
若 $\dfrac{\sqrt{3}}{2}b - \sqrt{3} > 0$，则 $\min(|b - 2|) = 1$，此时 $b \in \{1, 3 \}$，则 $\min \left( a - \dfrac{1}{2}b \right) = \dfrac{1}{2}$，则 $\left(a - \dfrac{1}{2}b \right)^2 + \left(\dfrac{\sqrt{3}}{2}b - \sqrt{3} \right)^2 + (c - 1)^2 = \dfrac{1}{2} + \dfrac{3}{4} + 0 > 1$。

故 $b = 2$，此时 $a = c = 1$（若 $a \neq 1$，$(a - \dfrac{1}{2}b)^2 = (a - 1)^2 \ge 1$，$c$ 同理）。

则 $a + b = 3, c - b = -1$，所求方程为 $x^2 - 2x - 3 = 0$。

22. 已知关于 $x$ 的方程 $x^2 - 2|x| + 2 = m$ 恰有 3 个实数根，求 $m$ 的值。

正解（换元法）：设 $A = |x|$，则 $A^2 - 2A + 2 = m$。我们发现：

当 $A = 0$ 时，会产生 1 个实数根。

否则，会产生 2 个实数根。

则因为原方程有 3 个实数根，且 $A$ 最多有 2 个不同的值，所以一定有 $A = 0$ 这一根.代入原方程得 $m = 2$。

23. 解方程：$\sqrt{x^2 + 12} + \sqrt{x^2 - 12} = 6 \sqrt{2}$。

解法 1（换元法）：我们设 $a, b$ 满足

\[\begin{cases} a \sqrt{2} = \sqrt{x^2 + 12} \\ b \sqrt{2} = \sqrt{x^2 - 12} \\ a \sqrt{2} + b \sqrt{2} = 6 \sqrt{2} \end{cases} \]
因为 $a \sqrt{2} + b \sqrt{2} = 6 \sqrt{2}$，所以 $b = 6 - a$。则

\[\begin{cases} a \sqrt{2} = \sqrt{x^2 + 12} \\ (6 - a) \sqrt{2} = \sqrt{x^2 - 12} \end{cases} \]
即

\[\begin{cases} 2a^2 = x^2 + 12 \\ 2(6 - a)^2 = x^2 - 12 \end{cases} \]
两式相减得 $2a^2 - 2(6 - a)^2 = 24 \implies 6(2a - 6) = 12 \implies a = 4$。则 $32 = x^2 + 12 \implies x^2 = 20 \implies x = \pm 2 \sqrt{5}$。

解法 2（换元法）：设 $m = \sqrt{x^2 + 12}, n = \sqrt{x^2 - 12}$。我们发现

\[\begin{cases} m^2 - n^2 = 24 \\ m + n = 6 \sqrt{2} \end{cases} \]
将 $m + n = 6 \sqrt{2}$ 代入 $m^2 - n^2 = 24$，则 $m - n = \dfrac{24}{6 \sqrt{2}} = \dfrac{24 \sqrt{2}}{12} = 2 \sqrt{2}$。

此时，容易得出 $m = 4 \sqrt{2}, n = 2 \sqrt{2}$。则 $\sqrt{x^2 - 12} = 2 \sqrt{2} \implies x^2 - 12 = 8 \implies x = \pm 2 \sqrt{5}$。

24. 已知 $b^2 - 4ac$ 是关于 $x$ 的二次方程 $ax^2 + bx + c = 0$ 的根，求 $ab$ 的范围。

正解：令 $t = b^2 - 4ac$，则 $(2at + b)^2 = b^2 - 4ac = t$，则 $x = t$ 是方程 $(2ax + b)^2 = x$ 的一个根。

展开该方程：

\[4a^2x^2 + (4ab - 1)x + b^2 = 0 \]
因为其有根，所以判别式

\[\begin{aligned} \Delta &= (4ab - 1)^2 - 16a^2b^2 \\ &= 16a^2b^2 - 8ab + 1 - 16a^2b^2 \\ &= 1 - 8ab > 0 \end{aligned} \]
则 $8ab < 1 \implies ab < 1/8$。

25. 已知关于 $x$ 的方程 $4x^2 - 8nx - 3x - 2 = 0$ 与 $x^2 - (n + 3)x - 2n^2 + 2 = 0$，求出这样的 $n$ 值，使第一个方程的两个实数根的平方差等于第二个方程的一整数根。

26. 若方程 $(x^2 - 1)(x^2 - 4) = k$ 有 4 个非零实根，且它们在数轴上对应的 4 个点等距排列，求 $k$ 的值。

解法 1：容易发现，这 4 个实根能被分成两对关于原点对称的实根。设 $A = x^2$，则 $(A - 1)(A - 4) = k \implies A^2 - 5A + (4 - k) = 0$。解得

\[A_1 = \dfrac{5 + \sqrt{4k + 9}}{2}, A_2 = \dfrac{5 - \sqrt{4k + 9}}{2} \]
此时可以发现 $A_1 > A_2$，故 4 个实根为（按大小递减排列）

\[\begin{aligned} x_1 &= \sqrt{A_1} \\ x_2 &= \sqrt{A_2} \\ x_3 &= -\sqrt{A_2} \\ x_4 &= -\sqrt{A_1} \end{aligned} \]
故 $x_1 - x_2 = x_2 - x_3$，即 $\sqrt{A_1} = 3 \sqrt{A_2} \implies A_1 = 9A_2$。代入 $A_1, A_2$ 得

\[\dfrac{5 + \sqrt{4k + 9}}{2} = \dfrac{45 - 9\sqrt{4k + 9}}{2} \]
即

\[5 + \sqrt{4k + 9} = 45 - 9 \sqrt{4k + 9} \]
解得 $k = \dfrac{7}{4}$。

解法 2（高次韦达定理）：容易发现，这 4 个实根能被分成两对关于原点对称的实根，则这些实根能被表示为 $x_1 = -3m, x_2 = -m, x_3 = m, x_4 = 3m$。根据韦达定理，

\[\begin{cases} x_1 x_2 x_3 x_4 = 9m^4 = 4 - k \\ x_1 x_2 + x_1 x_3 + x_1 x_4 + x_2 x_3 + x_2 x_4 + x_3 x_4 = 3m^2 + (-3m^2) + (-9m^2) + (-m^2) + (-3m^2) + 3m^2 = -10m^2 = -5 \end{cases} \]
故 $10m^2 = 5 \implies m^2 = \dfrac{1}{2}$，则 $4 - k = 9m^4 = (3m^2)^2 = \dfrac{9}{4}$。故 $k = \dfrac{7}{4}$。

27. 关于 $x$ 的方程 $x^2 - 5x = m^2 - 1$ 有实根 $x_1, x_2$ 满足 $|x_1| + |x_2| \le 6$，确定 $m$ 的取值范围。

正解（韦达定理）：原方程变形得 $x^2 - 5x + (1 - m^2) = 0$。则根据韦达定理可得，

\[\begin{cases} x_1 + x_2 = 5 \\ x_1 x_2 = 1 - m^2 \end{cases} \]
对 $|x_1| + |x_2| \le 6$ 平方，得

\[\begin{aligned} (|x_1| + |x_2|)^2 &= x_1^2 + x_2^2 + 2|x_1 x_2| \\ &= (x_1 + x_2)^2 - 2x_1 x_2 + 2|x_1 x_2| \\ &= 25 + 2|x_1 x_2| - 2x_1 x_2 \\ & \le 36 \end{aligned} \]
故 $2|x_1 x_2| - 2x_1 x_2 \le 11$。分类讨论 $x_1 x_2$ 的范围：

$x_1 x_2 \ge 0$：$2|x_1 x_2| - 2x_1 x_2 = 0 \le 11$。

$x_1 x_2 < 0$：$-4x_1 x_2 \le 11 \implies x_1 x_2 \ge -\dfrac{11}{4}$。

则 $x_1 x_2 \ge -\dfrac{11}{4}$，即 $m^2 - 1 \le \dfrac{11}{4} \implies m \le \dfrac{\sqrt{15}}{2}$。

28. 设实数 $a, b, c$ 满足：

$a \le b \le c$，
$ab + bc + ca = 0$，
$abc = 1$。

求最大的 $k$，满足 $|a + b| \ge k|c|$。

正解：由条件可知：$ab = \dfrac{1}{c}$，则 $ab + bc + ca = ab + (a + b)c = \dfrac{1}{c} + (a + b)c = 0$，则 $a + b = -\dfrac{1}{c^2}$。则

\[\begin{cases} a + b = -\dfrac{1}{c^2} \\ ab = \dfrac{1}{c} \end{cases} \]
这说明 $x_1 = a, x_2 = b$ 为方程 $x^2 + \dfrac{1}{c^2} x + \dfrac{1}{c} = 0$ 的两根。

为保证其有两根，考虑其判别式：

\[\begin{aligned} \Delta &= \dfrac{1}{c^4} - \dfrac{4}{c} \\ &= \dfrac{1 - 4c^3}{c^4} \\ & \ge 0 \end{aligned} \]
则 $1 - 4c^3 \ge 0 \implies c^3 \le \dfrac{1}{4}$。

再考虑 $|a + b| \ge k|c|$，则 $k \le \left| \dfrac{a + b}{c} \right| = \left| \dfrac{1}{c^3} \right|$。

考虑 $c$ 的符号：因为 $ab + bc + ca = 0$，所以 $\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} = 0$。则有两负一正或两正一负，故 $\dfrac{1}{c} > 0 \implies c > 0$。

则 $0 \le c^3 \le \dfrac{1}{4} \implies \dfrac{1}{c^3} \ge 4$，则 $k \le \dfrac{1}{4} \implies \max(k) = \dfrac{1}{4}$。

29. 求 $\dfrac{(2^3 - 1)(3^3 - 1)(4^3 - 1) \cdots (99^3 - 1)(100^3 - 1)}{(2^3 + 1)(3^3 + 1)(4^3 + 1) \cdots (99^3 + 1)(100^3 + 1)}$ 的值。

正解：原式变形为

\[\begin{aligned} &\dfrac{2^3 - 1}{2^3 + 1} \times \dfrac{3^3 - 1}{3^3 + 1} \times \dfrac{4^3 - 1}{4^3 + 1} \times \cdots \times \dfrac{99^3 - 1}{99^3 + 1} \times \dfrac{100^3 - 1}{100^3 + 1} \\ =& \prod_{n = 2}^{100} \dfrac{n^3 - 1}{n^3 + 1} \\ =& \prod_{n = 2}^{100} \dfrac{(n - 1)(n^2 + n + 1)}{(n + 1)(n^2 - n + 1)} \\ =& \left( \prod_{n = 2}^{100} \dfrac{n - 1}{n + 1} \right) \cdot \left( \prod_{n = 2}^{100} \dfrac{n^2 + n + 1}{n^2 - n + 1} \right) \end{aligned} \]
此时可以发现

\[\begin{aligned} \prod_{n = 2}^{100} \dfrac{n - 1}{n + 1} &= \dfrac{1}{3} \times \dfrac{2}{4} \times \dfrac{3}{5} \times \dfrac{4}{6} \times \cdots \times \dfrac{98}{100} \times \dfrac{99}{101} \\ &= \dfrac{1 \times 2}{100 \times 101} \\ &= \dfrac{1}{5050} \end{aligned} \]
同时

\[\begin{aligned} \prod_{n = 2}^{100} \dfrac{n^2 + n + 1}{n^2 - n + 1} &= \dfrac{7}{3} \times \dfrac{13}{7} \times \dfrac{21}{13} \times \cdots \times \dfrac{9901}{9703} \times \dfrac{10101}{9901} \\ &= \dfrac{10101}{3} \\ &= 3367 \end{aligned} \]
故所求的值为 $3367 \times \dfrac{1}{5050} = \dfrac{3367}{5050}$。

30. 因式分解：$x^2 + x^2 (x + 1)^2 + (x + 1)^2$。

正解：展开得 $x^4 + 2x^3 + 3x^2 + 2x + 1$。

发现其系数对称，故除以 $x^2$，得 $x^2 + 2x + 3 + 2/x + 1/x^2 = 3 + 2(x + 1/x) + (x^2 + 1/x^2)$。

设 $A = x + 1/x$，则可得 $3 + 2A + (A^2 - 2) = (A + 1)^2 + (x + 1 + 1/x)^2$。

故原式为 $(x^2 + x + 1)^2$。

31. 设 $x = 1 + 1/y, y = 1 + 1/x$，求 $x, y$ 的数量关系。

正解：发现 $x - y = 1/y - 1/x = \dfrac{x - y}{xy}$。此时有两种情况：

$xy = 1$：此时 $x = 1/y = 1 + 1/y$，故舍去此情况。

$x - y = 0$：此时 $x = y$。

故 $x = y$。

32. 设 $A = 1 - \dfrac{1}{2} + \dfrac{1}{3} - \dfrac{1}{4} + \cdots + \dfrac{1}{99} - \dfrac{1}{100}, B = \dfrac{1}{100 \times 102} + \dfrac{1}{100 \times 104} + \cdots + \dfrac{1}{100 \times 200}$，求 $A/B$ 的值。

正解：设 $S_n = \sum_{j = 1}^n 1/j$，我们尝试用 $S_n$ 表示 $A, B$。

容易发现

\[\begin{aligned} A &= \left( 1 + \dfrac{1}{2} + \dfrac{1}{3} + \cdots + \dfrac{1}{100} \right) - 2 \times \left( \dfrac{1}{2} + \dfrac{1}{4} + \cdots + \dfrac{1}{100} \right) \\ &= \left( 1 + \dfrac{1}{2} + \dfrac{1}{3} + \cdots + \dfrac{1}{100} \right) - \left( 1 + \dfrac{1}{2} + \dfrac{1}{3} + \cdots + \dfrac{1}{50} \right) \\ &= S_{100} - S_{50} \end{aligned} \]
同时

\[\begin{aligned} B &= \dfrac{1}{4} \times \left( \dfrac{1}{50 \times 51} + \dfrac{1}{50 \times 52} + \cdots + \dfrac{1}{50 \times 100} \right) \\ &= \dfrac{1}{4} \times \left( \dfrac{1}{50} \times \dfrac{1}{51} + \dfrac{1}{50} \times \dfrac{1}{52} + \cdots + \dfrac{1}{50} \times \dfrac{1}{100} \right) \\ &= \dfrac{1}{40} \times \dfrac{1}{50} \times \left( \dfrac{1}{51} + \dfrac{1}{52} + \cdots + \dfrac{1}{100} \right) \\ &= \dfrac{1}{200} \cdot (S_{100} - S_{50}) \\ &= \dfrac{1}{200} A \end{aligned} \]
故 $A/B = 200$。

33. 求证：$(1 + a)^n \ge 1 + na \quad (1 + a > 0, n \in \mathbb{N})$。

证明（归纳法）：当 $n = 1$ 时，$(1 + a)^1 \ge 1 + a$ 显然成立。

下面证明当 $(1 + a)^n \ge 1 + na$ 成立时，$(1 + a)^{n + 1} \ge 1 + (n + 1)a$ 成立。

我们发现，只需证明 $(1 + a)^n \ge \dfrac{1 + (n + 1) a}{1 + a}$ 即可。

又因为 $(1 + a)^n \ge 1 + na$，所以只需证明 $\dfrac{1 + (n + 1) a}{1 + a} \le 1 + na$。

则：

\[\begin{aligned} na^2 \ge 0 &\implies 1 + (n + 1) a + na^2 \ge 1 + (n + 1) a \\ &\implies (1 + a)(1 + na) \ge 1 + (n + 1) a \\ &\implies 1 + na \ge \dfrac{1 + (n + 1) a}{1 + a} \\ &\implies (1 + a)^n \ge 1 + na \ge \dfrac{1 + (n + 1) a}{1 + a} \\ &\implies (1 + a)^{n + 1} \ge 1 + (n + 1) a \end{aligned} \]
故原命题成立。

34. 已知 $a - \dfrac{1}{a} = 1$，求 $a^{12} + 48 a^{-4}$ 的值。

正解 ^[1]：想把次数变得对称，故变换原式为 $a^4 (a^8 + 48 a^{-8})$。

注意到 $a^4 + a^{-4} = 7 \implies a^8 + a^{-8} = (a^4 + a^{-4})^2 - 2 = 47$，与 $48$ 只差 $1$，故原式为

\[\begin{aligned} a^4 (a^8 + 48 a^{-8}) &= a^4 (a^8 + (47 + 1) a^{-8}) \\ &= a^4 (a^8 + a^{-8} + (a^8 + a^{-8})a^{-8}) \\ &= a^4 (47 + 47 a^{-8}) \\ &= 47a^4 + 47a^{-4} \\ &= 47 \cdot 7 \\ &= 329 \end{aligned} \]

35. 已知直角三角形的周长为 $m$，求面积的最大值。

正解：设两直角边分别有 $a, b$ 的边长，则 $a^2 + b^2 = (m - a - b)^2$。

则 $m^2 - 2(a + b)m + 2ab = 0$。

设面积为 $S = \dfrac{ab}{2}$，则：

\[4S = 2(m - c)m - m^2 = m^2 - 2cm \tag{1} \]
此时，我们想让 $c$ 最小。

注意到 $a^2 + b^2 = c^2 \ge 2ab$。

故 $2c^2 = 2(a^2 + b^2) \ge a^2 + b^2 + 2ab = (a + b)^2 = (m - c)^2$。

又因为 $c, m \ge 0$，所以 $\sqrt{2} c \ge m - c$，所以 $c \ge \dfrac{m}{1 + \sqrt{2}} = (\sqrt{2} - 1)m$。

故 $c_{\min} = (\sqrt{2} - 1)m$，代入 $(1)$ 式得 $S = \dfrac{(3 - \sqrt{2})m^2}{4}$。

36. 已知 $x_1, x_2$ 是方程 $x^2 + 5x + 2 = 0$ 的两个实数根，求 $\sqrt{\dfrac{x_1}{x_2}} + \sqrt{\dfrac{x_2}{x_1}}$ 的值。

正解（韦达定理）：根据韦达定理，$x_1 + x_2 = -5, x_1 x_2 = 2$，则 $x_1, x_2 < 0$。此时原式的平方为

\[\begin{aligned} \left(\sqrt{\dfrac{x_1}{x_2}} + \sqrt{\dfrac{x_2}{x_1}} \right)^2 &= \dfrac{x_1}{x_2} + \dfrac{x_2}{x_1} + 2 \sqrt{\dfrac{x_1 x_2}{x_2 x_1}} \\ &= \dfrac{x_1}{x_2} + \dfrac{x_2}{x_1} + 2 \cdot 1 \\ &= \dfrac{x_1^2 + x_2^2}{x_1 x_2} + 2 \\ &= \dfrac{(x_1 + x_2)^2 - 2x_1 x_2}{x_1 x_2} + 2 \\ &= \dfrac{(-5)^2}{2} = \dfrac{25}{2} \end{aligned} \]
则原式为 $\sqrt{\dfrac{25}{2}} = \dfrac{5}{\sqrt{2}} = \dfrac{5}{2} \sqrt{2}$。

评注：对于这题，一个典型错误为 $\sqrt{\dfrac{x_1}{x_2}} + \sqrt{\dfrac{x_2}{x_1}} = \dfrac{\sqrt{x_1}}{\sqrt{x_2}} + \dfrac{\sqrt{x_2}}{\sqrt{x_1}}$。这时我们不能保证根号下非负，故错误。但是可以利用 $x_1, x_2 < 0$ 的结论将原式变为 $\dfrac{\sqrt{-x_1}}{\sqrt{-x_2}} + \dfrac{\sqrt{-x_2}}{\sqrt{-x_1}}$。

37. 设多项式 $f(x), g(x)$ 满足：

不低于一次。
最高次项系数为正。
系数都是整数。
$f(x) g(x) = 16x^6 - 25x^4 - 2x^2 - 1$。

求 $f(3) + g(3)$ 的值。

正解：考虑因式分解，猜测 $\deg(f) = \deg(g) = 3$。

说明：这样猜是因为 $\deg(f) = 4, \deg(g) = 2$ 不对。

设 $f = 4x^3 + ax^2 + bx + 1, g = 4x^3 + cx^2 + dx - 1$，观察一次项和五次项可得 $b = d, a = -c$，则 $g = 4x^3 - ax^2 + bx - 1$。

观察其它项可得：

\[\begin{cases} 2a - b^2 = 2 \\ a^2 - 8b = 25 \end{cases} \]
解得 $a = 3, b = -2$，则 $f = 4x^3 + 3x^2 - 2x + 1, g = 4x^3 - 3x^2 - 2x - 1$。

则 $f(3) + g(3) = 8 \cdot 3^3 - 4 \cdot 3 = 204$。

38. 方程 $x^2 = a|x - a| - a$ 有两个不同实根，求 $a$ 的范围。

正解：注意到 $a \neq 0$，则方程 $x^2 = a|x - a| - a \iff \dfrac{x^2}{a} + 1 = |x - a|$。

设 $f(x) = \dfrac{1}{a} x^2 + 1, g(x) = |x - a|$。

$a > 0$：因为 $f(x) > 0$，所以我们可以把 $g$ 拆成两个函数：$g_1(x) = x - a, g_2(x) = a - x$。

容易发现，$f(x) = g_1(x)$ 一定无实根。

说明：判别式为 $\Delta = -3 - \dfrac{4}{a}$，因为 $a > 0$，所以 $\Delta < 0$，方程无实根。

且在 $a > \dfrac{4}{5}$ 时，$f(x) = g_2(x)$ 有两个不同实根。

说明：判别式为 $\Delta = 5 - \dfrac{4}{a}$，因为需要 2 个不同实根，所以 $\Delta > 0 \iff a > \dfrac{4}{5}$。

故此时 $a > \dfrac{4}{5}$。

$a < 0$：设 $a = a_0$ 时方程有 1 个解，则 $a_0 < a$ 时方程有 2 个解。

而在 $g(x)$ 与 $f(x)$ 相切的时候有 1 个解，且这个解 $x_0 > a$，所以我们限制 $g(x)$ 的定义域为 $(a, +\infty)$。

因为 $g(x)$ 与 $f(x)$ 相切，所以 $f'(x) = g'(x) = 1 \iff x = \dfrac{a_0}{2}$，则切点为 $\left( \dfrac{a_0}{2}, \dfrac{a_0}{4} + 1 \right)$，切线为 $y = x - \dfrac{a_0}{4} + 1$，与 $x$ 轴交于 $\left( \dfrac{a_0}{4} - 1, 0 \right)$。

而因为 $g(x)$ 与 $f(x)$ 相切，所以切线与 $x$ 轴交于 $(a, 0)$，所以 $\dfrac{a_0}{4} - 1 = a_0 \iff a_0 = -\dfrac{4}{3}$。

故 $a > -\dfrac{4}{3}$。

综上，$a \in \left( \dfrac{4}{5}, +\infty \right) \cup \left( -\dfrac{4}{3}, 0 \right)$。

39. 已知 $a, b$ 为正实数，且 $a + 4b + 3 = ab$，求 $\min(ab)$。

正解：则 $a + 4b = ab - 3 \ge 4 \sqrt{ab}$。

设 $t = ab$，则 $t - 3 \ge 4 \sqrt{t} \iff (t - 3)^2 = t^2 - 22t + 9 \ge 0 \iff t \in (-\infty, -4 \sqrt{7} + 11] \cup [4 \sqrt{7} + 11, +\infty)$。

因为 $a + 4b > 0$，所以 $a + 4b + 3 = ab > 3$，所以 $ab \in [4 \sqrt{7} + 11, +\infty)$。

故 $\min(ab) = 4 \sqrt{7} + 11$。

40. 设 $a \in \R$，若 $x > 0$ 时，均有 $((a - 1)x - 1)(x^2 - ax - 1) \ge 0$，求 $a$ 的值。

正解：因为 $x^2 - ax - 1$ 开口向上，所以 $a - 1 > 0 \iff a > 1$。

根据题目条件，$(a - 1)x - 1$ 和 $x^2 - ax - 1$ 同号。

则它们的交点在 $x$ 轴上，即它们有公共根。

$(a - 1)x - 1$ 的根是 $x = \dfrac{1}{a - 1} > 0$，则 $x = \dfrac{1}{a - 1}$ 也是 $x^2 - ax - 1$ 的根。

根据韦达定理，$x^2 - ax - 1$ 的另一根为 $x = 1 - a$。

把 $x = 1 - a$ 代入 $x^2 - ax - 1 = 0$，解得 $a = \dfrac{3}{2}$。

41. 已知 $x, y, z \in \R^+$，且 $x + y + z = 1$，求证：

\[\dfrac{1}{1 - x} + \dfrac{1}{1 - y} + \dfrac{1}{1 - z} \ge \dfrac{2}{1 - x} + \dfrac{2}{1 - y} + \dfrac{2}{1 - z} \]

证明：由权方和不等式得：

\[\dfrac{1}{1 - x} + \dfrac{1}{1 - y} \ge \dfrac{4}{2 - x - y} = \dfrac{4}{1 + z} \]
同理有：

\[\dfrac{1}{1 - y} + \dfrac{1}{1 - z} \ge \dfrac{4}{1 + x} \\ \dfrac{1}{1 - z} + \dfrac{1}{1 - x} \ge \dfrac{4}{1 + y} \]
三式相加得：

\[2 \left( \dfrac{1}{1 - x} + \dfrac{1}{1 - y} + \dfrac{1}{1 - z} \right) \ge 2 \left( \dfrac{2}{1 - x} + \dfrac{2}{1 - y} + \dfrac{2}{1 - z} \right) \]
两边除以 $2$ 即可。

几何篇

1. 已知 $x^3 + y^3 = 16$，求 $xy$ 的最大值。

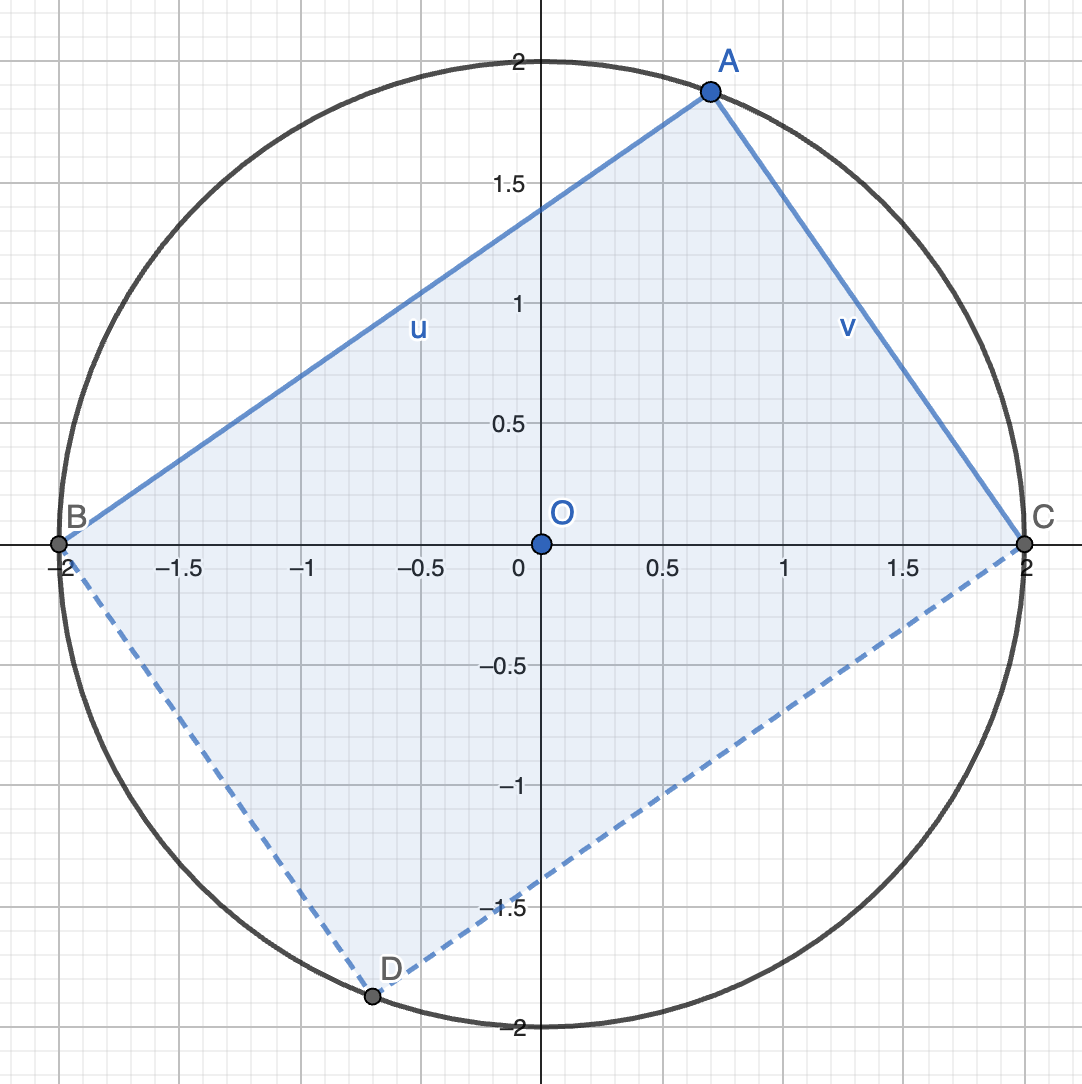
正解（面积法）：设 $u = a^{1.5}, v = b^{1.5}$。则 $u^2 + v^2 = 16$。

考虑其图象（半径为 2、以原点为圆心的圆）。如图，$u = AB, v = AC, uv = S_{ABDC}$。

容易发现，在 $AD \perp BC$ 时，$S_{ABDC}$ 最大，为 8。此时 $(ab)^{1.5} = uv = 8$。

则 $(ab)^3 = 64 \implies ab = 4$。

故最大值为 4。

2. 如图，已知：

$\triangle ABC$。
$AB > AC$。
$\angle BAC$ 的角平分线与 $BC$ 的中垂线交于点 $D$。
$DF \perp AB$ 于点 $F$。

求证：$AB = AC + 2BF$。

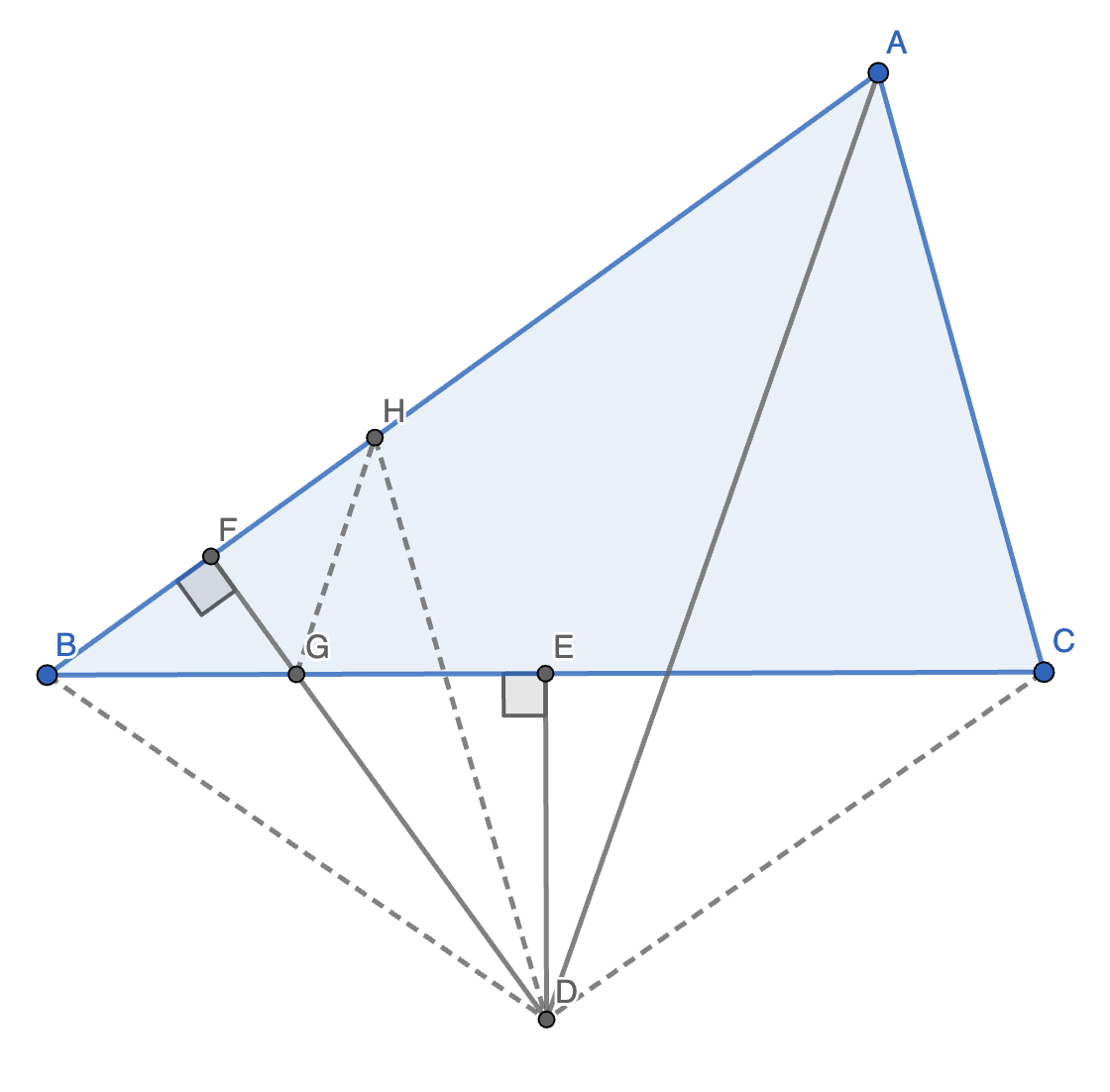
证明：连接 $BD, CD$。在 $AF$ 上取点 $H$ 使得 $AH = AC$。连接 $DH, GH$。（技巧：把条件集中到一起。）

在 $\triangle ACD$ 和 $\triangle ADH$ 中，

\[\begin{cases} AC = AH \\ \angle CAD = \angle DAH \\ AD = AD \end{cases} \]
故 $\triangle ACD \cong \triangle AHD \implies CD = DH$。

又因为 $DE$ 是 $BC$ 的中垂线，所以 $BD = CD = DH$，所以 $\triangle BGH$ 是等腰三角形。

这说明 $BF = FH$，则 $AB = AH + FH + BF = AC + 2BF$。

故原命题得证。

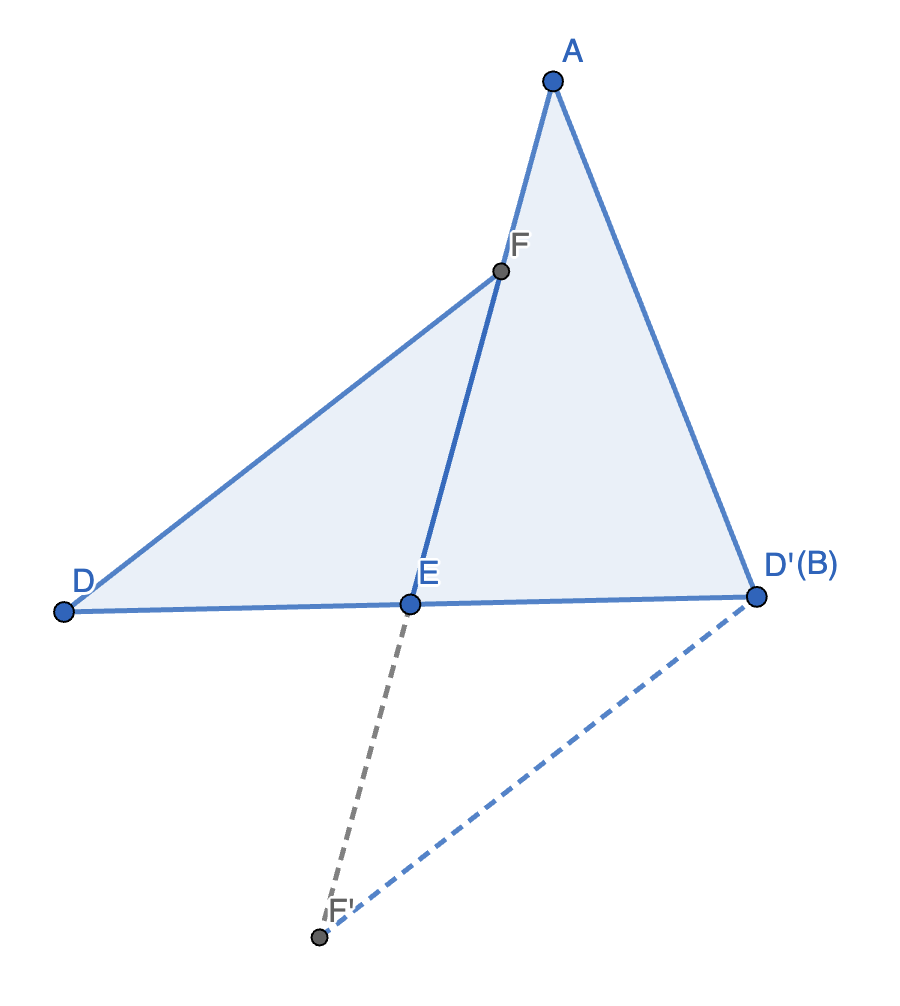
3. 如图，已知 $BE = DE, AB = DF$。求证：$\angle A = \angle DFE$。

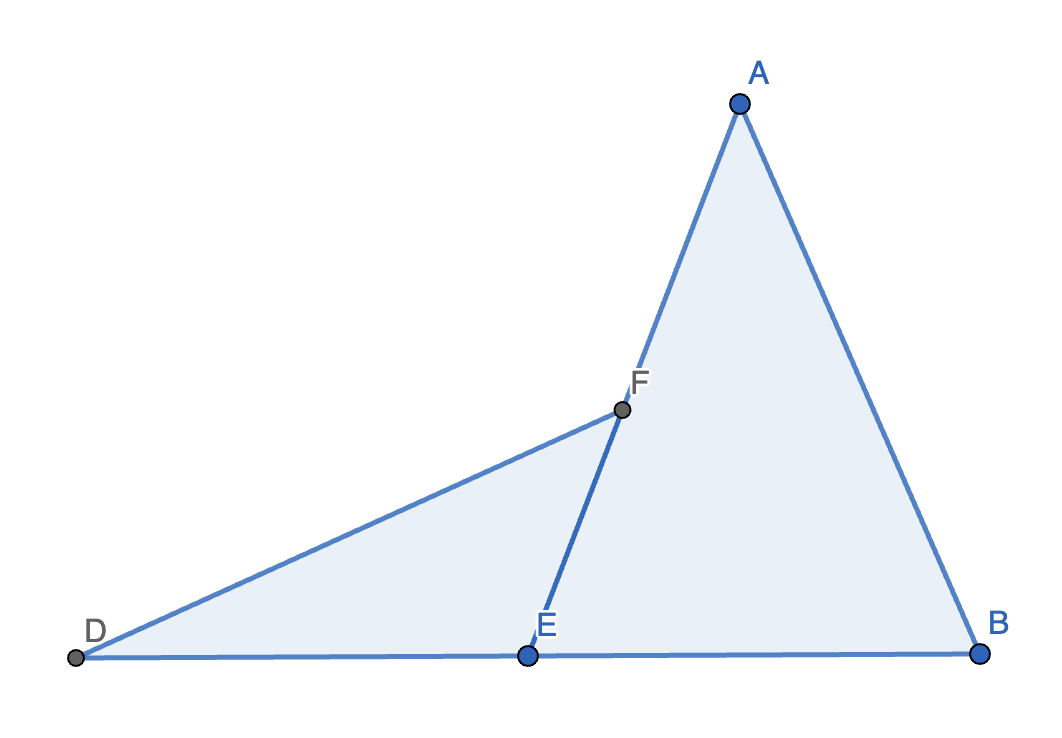
证明 1：作 $BG \perp AE, DH \perp AE$，则 $BG \parallel DH \implies \angle EBG = \angle EDH$。

则在 $\triangle DEH$ 和 $\triangle BEG$ 中，

\[\begin{cases} \angle H = \angle BGE \\ \angle EBG = \angle EDH \\ BE = DE \end{cases} \]
故 $\triangle DEH \cong \triangle BEG \implies BG = DH$。

则在 $\text{Rt} \triangle DFH$ 与 $\text{Rt} \triangle BAG$ 中，

\[\begin{cases} AB = DF \\ BG = DH \end{cases} \]
故 $\triangle DFH \cong \triangle BAG \implies \angle DFE = \angle A$，故原命题得证。

证明 2：延长 $FE$ 至 $F'$ 使得 $EF = EF'$，连接 $BF'$。

此时在 $\triangle DEF$ 和 $\triangle BEF'$ 中，

\[\begin{cases} EF = EF' \\ \angle DEF = \angle BEF' \\ BE = DE \end{cases} \]
故 $\triangle DEF \cong \triangle BEF' \implies BF' = DF = AB, \angle F' = \angle DFE$。

故 $\triangle ABF'$ 为等腰三角形，$\angle A = \angle F' = \angle DFE$。

原命题得证。

4. 如图，已知：

$C$ 是线段 $AB$ 上任意一点。
$AC = CD = AD, BC = CE = BE$。

求证：$CF = CG$。

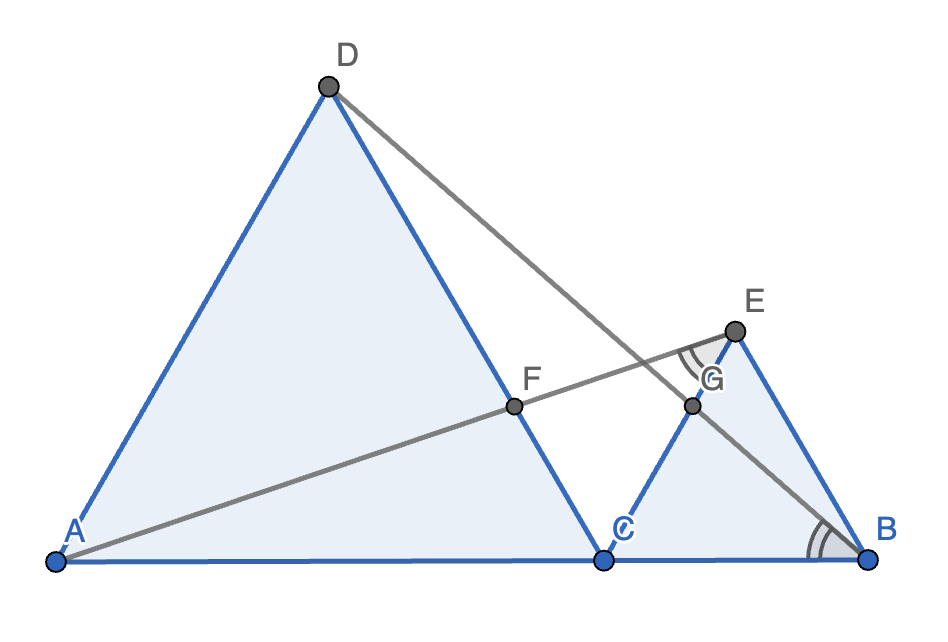
证明：容易发现，$\triangle ACD$ 和 $\triangle BCE$ 均为等边三角形，故 $\angle ACD = \angle DCE = \angle BCE = 60 \degree$。

在 $\triangle ACE$ 和 $\triangle BCD$ 中，

\[\begin{cases} AC = CD \\ \angle ACE = \angle BCD = 120 \degree \\ BC = CE \end{cases} \]
故 $\triangle ACE \cong \triangle DCB \implies \angle CBD = \angle AEC$。

则在 $\triangle CEF$ 和 $\triangle CBG$ 中，

\[\begin{cases} \angle CBD = \angle AEC \\ \angle BCE = \angle ECF \\ BC = CE \end{cases} \]
则 $\triangle CEF \cong \triangle CBG \implies CF = CG$，故原命题得证。

5. 如图，在 $\triangle ABC$ 的 $AC, BC$ 两边向外作正方形 $ACDE, BCGF$，连接 $EF$，且 $BC \parallel EF$。求证：$AB = AC$。

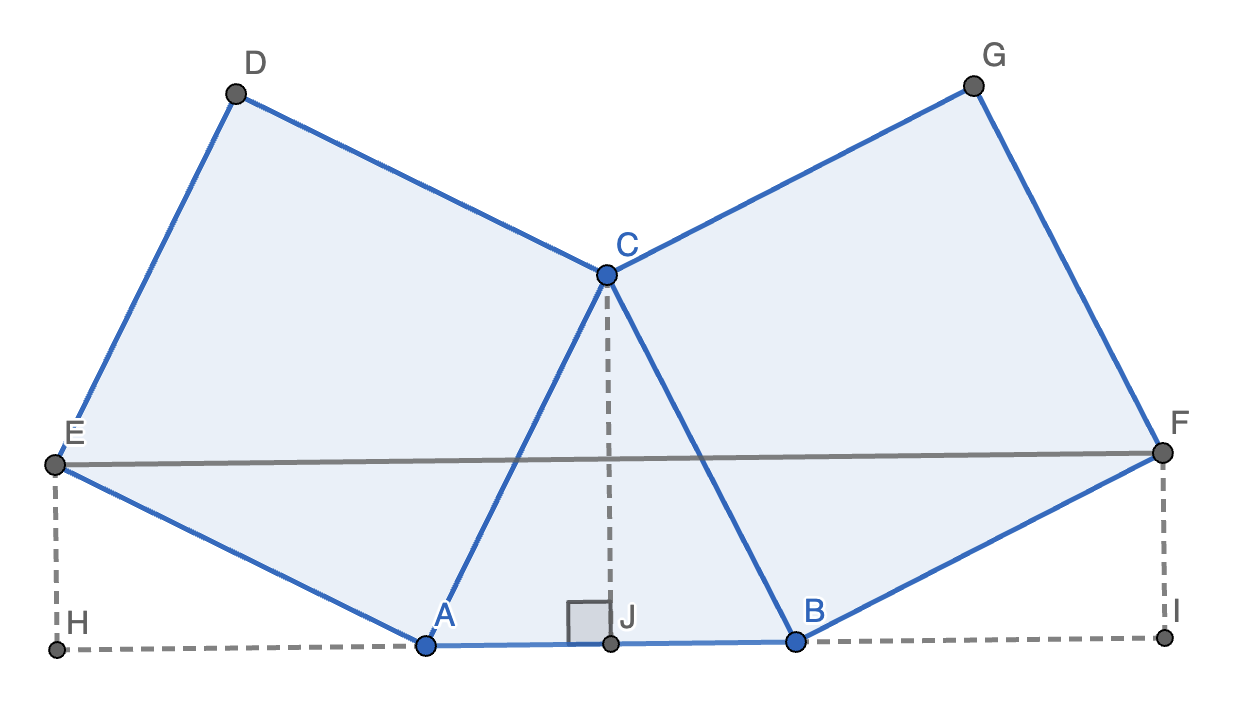
证明：作 $EH \perp AB, FI \perp AB$，作 $CJ \perp AB$ 交 $AB$ 于点 $J$。设 $\angle ACJ = \alpha, \angle BCJ = \beta$。

可以发现，$\angle CAJ = 90 \degree - \alpha, \angle CBJ = 90 \degree - \beta$。

故 $\angle EAH = 90 \degree - \angle CAJ = \alpha, \angle FBI = 90 \degree - \angle CBJ = \beta$。

故 $\angle AEH = 90 \degree - \angle EAH = \alpha, \angle BFI = 90 \degree - \angle FBI = \beta$。

在 $\triangle ACJ$ 和 $\triangle AEH$ 中，

\[\begin{cases} \angle ACJ = \angle EAH = \alpha \\ AC = AE \\ \angle AEH = \angle CAJ = 90 \degree - \alpha \end{cases} \]
故 $\triangle ACJ \cong \triangle AEH \implies AJ = EH$。

同理可得，$\triangle BCJ \cong \triangle BFI \implies BJ = FI$。

因为 $BC \parallel EF$，所以 $EH = FI$，即 $AJ = BJ$。

则 $CJ$ 为中垂线，则 $\triangle ABC$ 为等腰三角形。故 $AB = AC$，原命题得证。

6. 如图，在 $\text{Rt} \triangle ABC$ 中，$\angle ACB = 90 \degree$，$D$ 为 $\triangle ABC$ 内一点，连接 $BD, DC$，延长 $DC$ 至点 $E$，使得 $CE = CD$，连接 $AE$ 交 $BD$ 于点 $H$，连接 $CH$。若 $AB^2 = AE^2 + BD^2$，求线段 $CD$ 与 $CH$ 的数量关系。

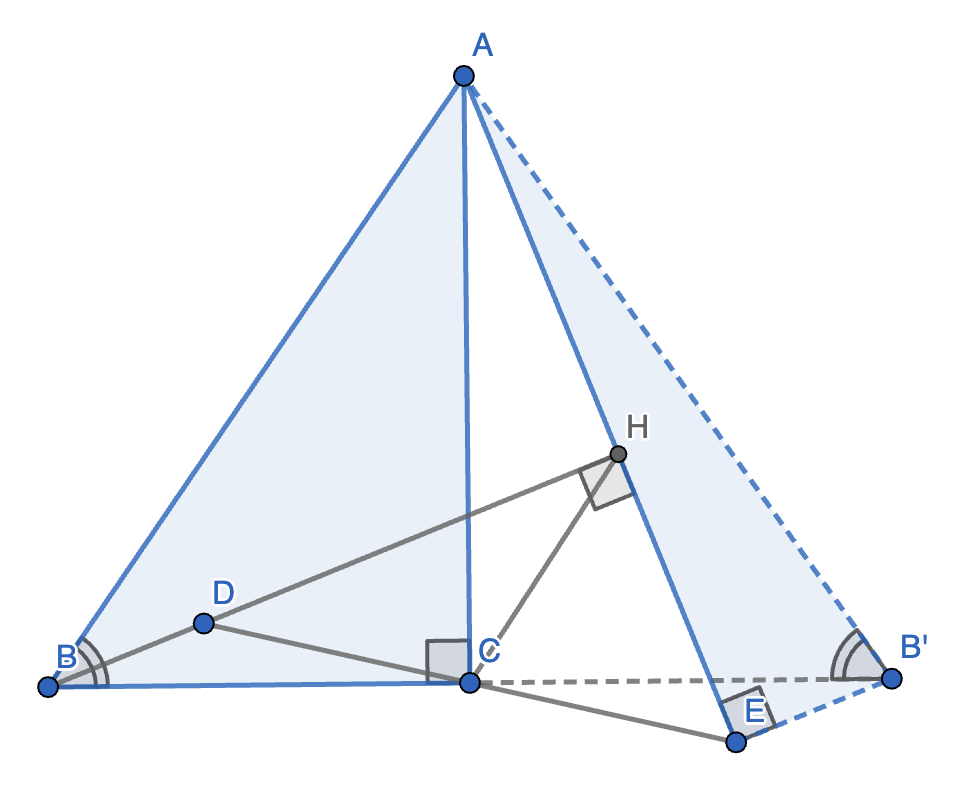
正解：延长 $BC$ 至 $B'$ 满足 $B'C = BC$，连接 $B'E$.

在 $\triangle BCD$ 与 $\triangle B'CE$ 中，

\[\begin{cases} CD = CE \\ \angle BCD = \angle B'CE \\ BC = B'C \end{cases} \]
故 $\triangle BCD \cong \triangle B'CE \implies \angle BDC = \angle B'EC \implies BD \parallel B'E \implies \angle BHE = 90 \degree$。

又因为 $CD = CE$，所以 $CD = CE = CH，故原命题得证。

7. 如图，已知点 $I$ 为 $\triangle ABC$ 的角平分线的交点。若 $AB + BI = AC, \angle BAC = 60 \degree$，求 $\angle AIB$ 的度数。

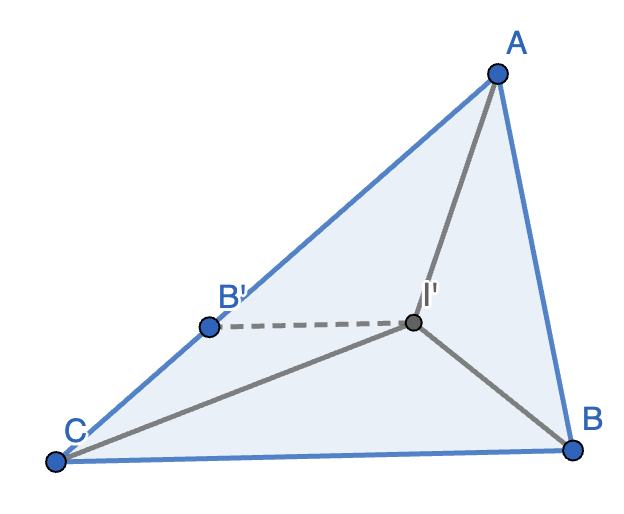
正解：在 $AC$ 上取点 $B'$ 使得 $AB' = AB$，连接 $B'I$。

在 $\triangle ABI$ 与 $\triangle AB'I$ 中，

\[\begin{cases} AB = AB' \\ \angle BAI = \angle B'AI \\ AI = AI \end{cases} \]
故 $\triangle ABI \cong \triangle AB'I \implies BI = B'I$。

又有 $AB + BI = AC$，故 $B'C = BI = B'I$。

则因为 $B'C = B'I$，所以 $\angle B'CI = \angle B'IC$。

又因为 $CI$ 为 $\angle ACB$ 的角平分线，所以 $\angle B'CI = \angle BCI = \angle B'IC \implies B'I \parallel BC$。

故四边形 $B'IBC$ 为等腰梯形，故 $\angle CBI = \angle ACB$。

又知 $\angle ABC + \angle ACB + 60 \degree = 180 \degree \implies 2 \angle CBI + \angle ACB = 120 \degree \implies 3 \angle ACB = 120 \degree \implies \angle ACB = 40 \degree$。

故 $\angle ABI = 2 \angle CBI = 2 \angle ACB = 80 \degree$。

故 $\angle AIB = 180 \degree - \dfrac{1}{2} \angle BAC - \angle ABI = 110 \degree$。

8. 如图，在 $\triangle ABC$ 中，$\angle B = 90 \degree$，点 $D$ 为斜边 $AC$ 上一点，以 $AD$ 为直径的 $\odot O$ 与 $BC$ 相切于点 $E$，交 $AB$ 于点 $F$。若 $AD = 4, AF = 2BF$，求弧 $\overparen{DF}$ 的长。

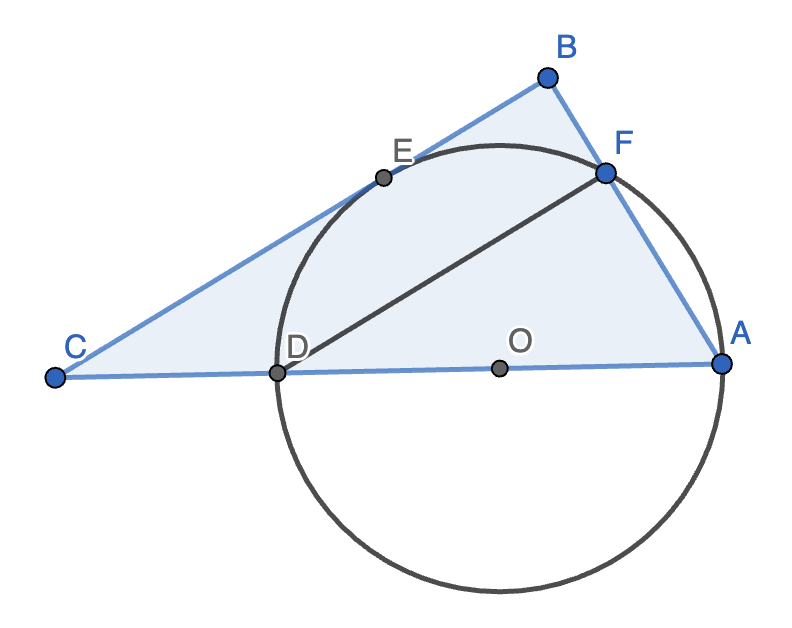
正解：连接 $OE, OF$，设 $OE$ 与 $DF$ 相交于点 $G$。

因为 $AD$ 为直径，所以 $\angle AFD = \angle BFG = 90 \degree$。

又因为 $BC$ 为 $\odot O$ 的切线，所以 $\angle OEB = 90 \degree$。

又因为 $\angle B = 90 \degree$，所以 $\angle EGF = 90 \degree, BF = EG$。

因为 $OE$ 为 $\odot O$ 的半径，所以 $DG = FG$。

因为 $OD = OA$，所以 $OG$ 为 $\triangle ADF$ 的中位线，所以 $AF = 2OG$。

因为 $AF = 2BF$，所以 $BF = OG = EG$，所以 $2OG = OE = OF$。

因为在 $\triangle OGF$ 中，$\cos(\angle GOF) = \dfrac{OG}{OF} = \dfrac{1}{2}$，所以 $\angle GOF = 60 \degree$。

因为 $\overparen{EF} = \overparen{DE}$，所以 $\angle GOF = \angle DOG = 60 \degree$，所以 $\angle DOF = 120 \degree$，所以 $\overparen{DF}$ 的长为 $\dfrac{120 \pi \cdot 2}{180} = \dfrac{4 \pi}{3}$。

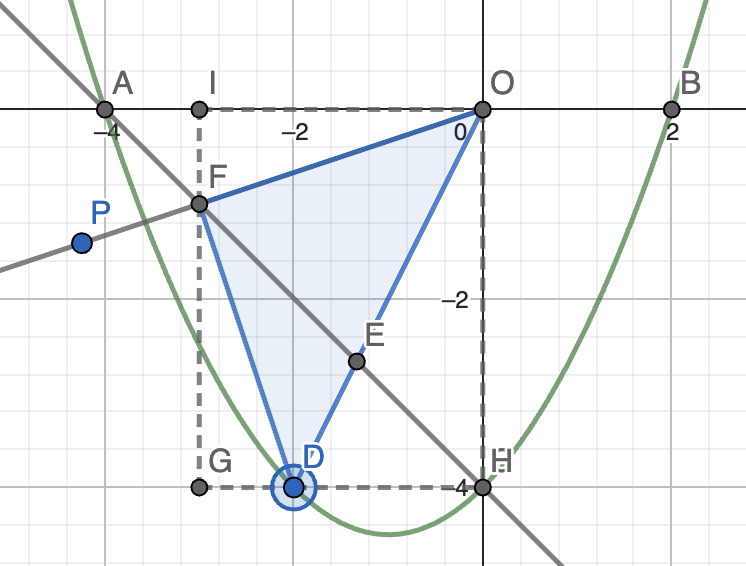
9. 如图，抛物线 $y = \dfrac{1}{2} x^2 + x - 4$ 与 $x$ 轴交于 $A, B$ 两点，与 $y$ 轴交于点 $C(0, -4)$，点 $D$ 为 $x$ 轴下方抛物线上的动点（不与点 $C$ 重合），射线 $OD$ 交直线 $AC$ 于点 $E$，将射线 $OD$ 绕点 $O$ 顺时针旋转 $45 \degree$ 得到射线 $OP$ 交直线 $AC$ 于点 $F$，连接 $DF$。若 $\triangle ODF$ 为直角三角形，求点 $D$ 的坐标。

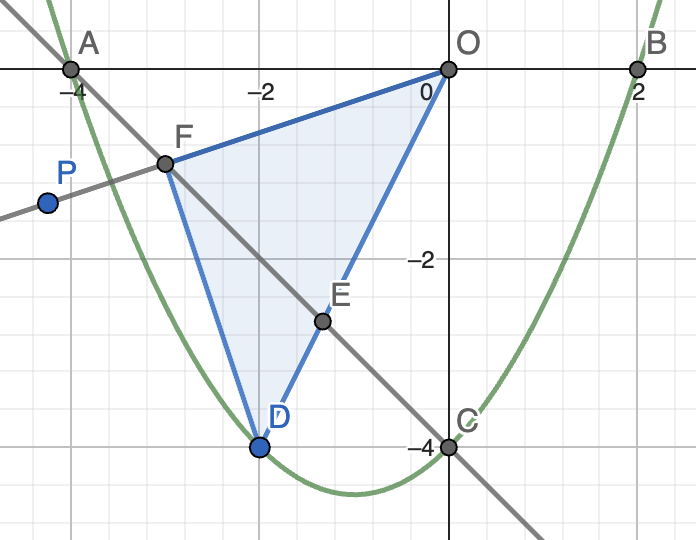
思路：本题通过全等将不同的边变换到 $D$ 与 $x$ 轴的垂线上，从而求出 $y_D$，最后解出 $x_D$。因为此题中 $x_D$ 不好直接求，故先求 $y_D$。想求 $y_D$，需要利用已有的坐标，其中点 $F$ 的坐标是已知的，且不在坐标轴上，有更多信息。虽然其坐标带有未知数，但可以消去。

正解：容易发现，$A(-4, 0), B(2, 0)$。

设直线 $AC$ 的解析式为 $y = kx + b$，则：

\[\begin{cases} 0 = -4k + b \\ -4 = b \end{cases} \]
解得 $k = 1, b = -4$，所以 $AC$ 的解析式为 $y = -x - 4$。

设 $F(t, -t - 4) \quad (t < 0)$，分类讨论 $\triangle ODF$ 的直角的位置：

$\angle DFO$ 为直角：如图，过点 $F$ 作 $GI \perp OA$，作 $DG \perp OC$ 交 $GI$ 于点 $G$。

因为 $\angle DOF = 45 \degree$，所以 $OD = OF$。

又知 $\angle OFI + \angle FOI = \angle OFI + DFG = 90 \degree \implies \angle DFG = \angle FOI$，同理可得 $\angle OFI = \angle FDG$。

故 $\triangle OFI \cong \triangle FDG \implies FG = OI = t$。

故 $IG = FI + FG = -t - 4 + t = -4$，所以 $D(x_D, -4)$。

因为 $D$ 在抛物线上，所以 $\dfrac{1}{2} x_D^2 + x_D - 4 = -4 \implies x_D^2 + 2x_D = 0 \implies x_D = -2$（$x_D = 0$ 舍去）。

故 $D(-2, -4)$。

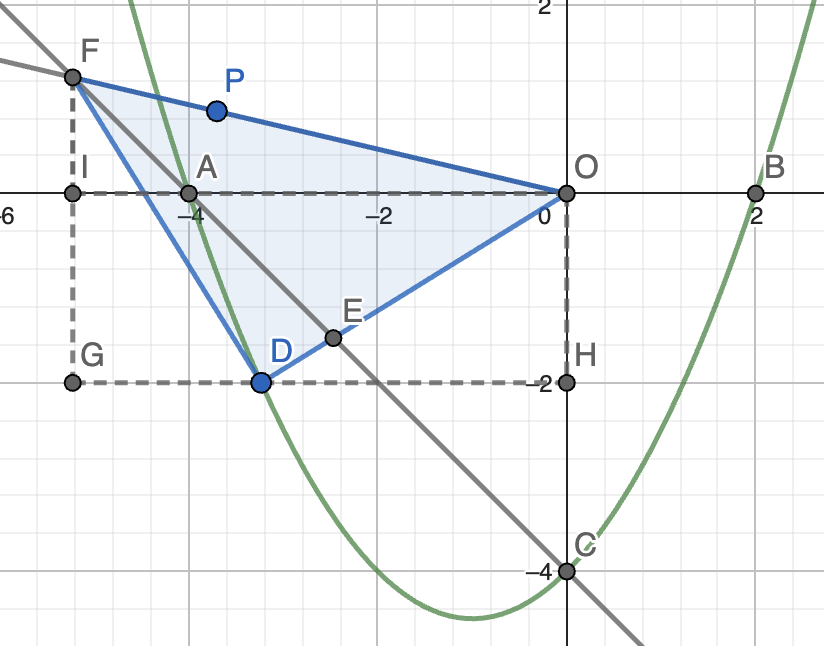
$\angle FDO$ 为直角：如图，作 $FG \perp OA$，$GJ \perp OC$ 交直线 $OC$ 于点 $J$，连接 $OJ$。

同理可得 $\triangle DFG \cong \triangle DOJ \implies DJ = FG, DG = OJ$。

故 $DM + ND = FN + OM = -t, -t - 4 + OM = FN$。

故 $y_D = -OM = -2$。

则 $\dfrac{1}{2} x_D^2 + x_D - 4 = -2 \implies x_D = \pm \sqrt{5} - 1$。

故 $D(\sqrt{5} - 1, -2)$ 或 $D(-\sqrt{5} - 1, -2)$。

综上所述，$D(-2, -4)$ 或 $D(\sqrt{5} - 1, -2)$ 或 $D(-\sqrt{5} - 1, -2)$。

10. 如图，在 $\triangle ABC$ 中，$AD \perp BC, BF \perp AC$，过 $D$ 作 $AB$ 的垂线交 $AB$ 于点 $E$，交 $BF$ 于点 $H$，交 $AC$ 于点 $G$。求证：$DE^2 = EG \cdot EH$。

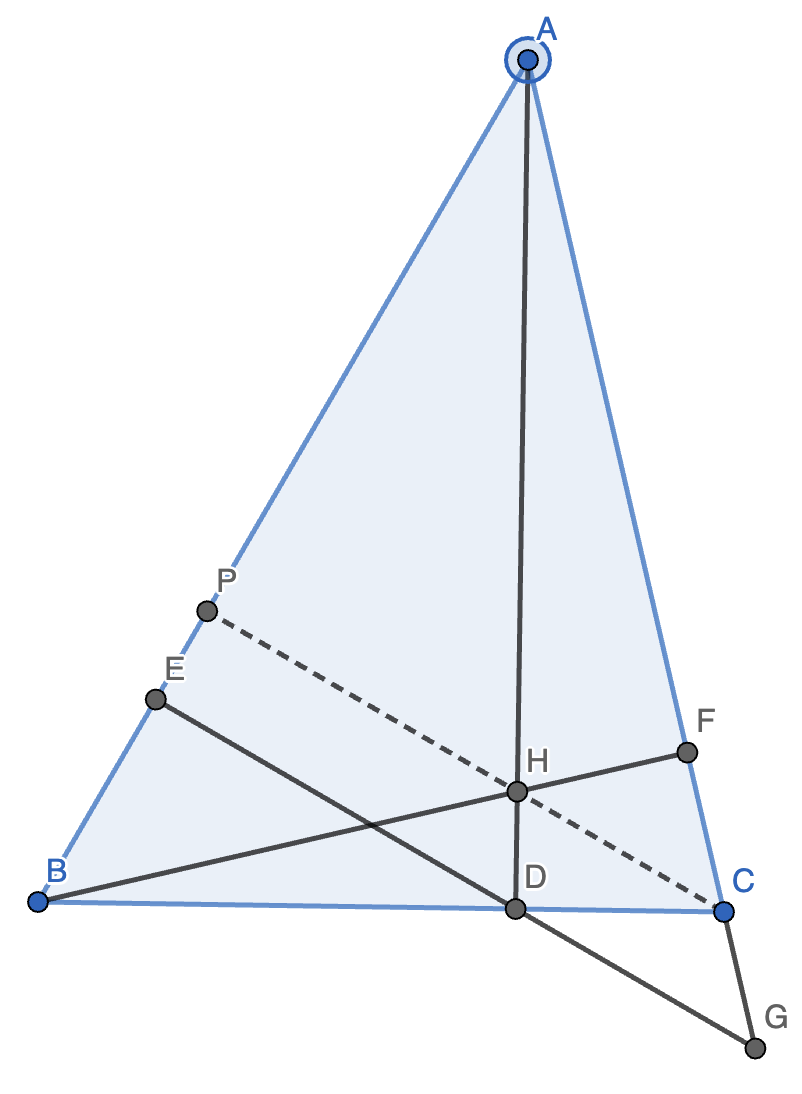
证明：如图，作 $CP \perp AB$ 交 $AD$ 于点 $H$。（技巧：在见到垂心的两个高都被作出来时，可以尝试把第三个也作出来。）

容易发现，$\dfrac{DE}{EG} = \dfrac{HP}{CP}, \dfrac{EH}{DE} = \dfrac{HP}{CP} = \dfrac{DE}{EG}$，故 $DE^2 = EG \cdot EH$，原命题成立。

评注：本题的辅助线，成功创造了两对相似三角形，将条件结合到了一起，非常的妙！

11. 在 $\triangle ABC$ 中，$BC = 6$，$BC$ 上的高 $AD = 3$，作 $\triangle ABC$ 的一个内接正方形，使得它的两个顶点都在 $AB$ 和 $AC$ 上，求该正方形的边长。

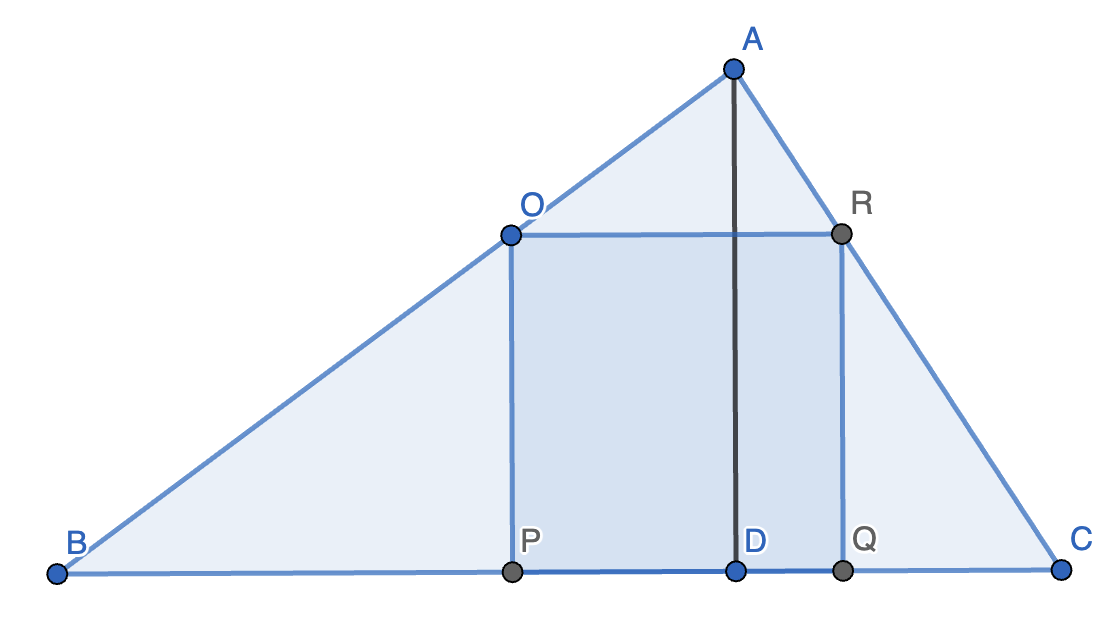
解法 1：设正方形的边长为 $x$，$OR$ 交 $AD$ 于点 $P$，则 $AP = 3 - x$。

因为 $\triangle AOR \sim \triangle ABC$，所以 $\dfrac{AS}{OR} = \dfrac{AD}{BC}$，即 $\dfrac{3 - x}{x} = \dfrac{3}{6}$，解得 $x = 2$。

解法 2：设 $AR = x_1, AO = y_1, CR = ax_1, BO = ay_1, DQ = x_2, DP = y_2, x = x_2 + y_2$，$OR$ 交 $AD$ 于点 $P$。

则 $AP = \dfrac{3}{a + 1}, DP = \dfrac{3a}{a + 1}$。

则可列方程组：

\[\begin{cases} (a + 1) x = 6 \\ x = \dfrac{3a}{a + 1} \end{cases} \]
解得 $a = 2, x = 2$。

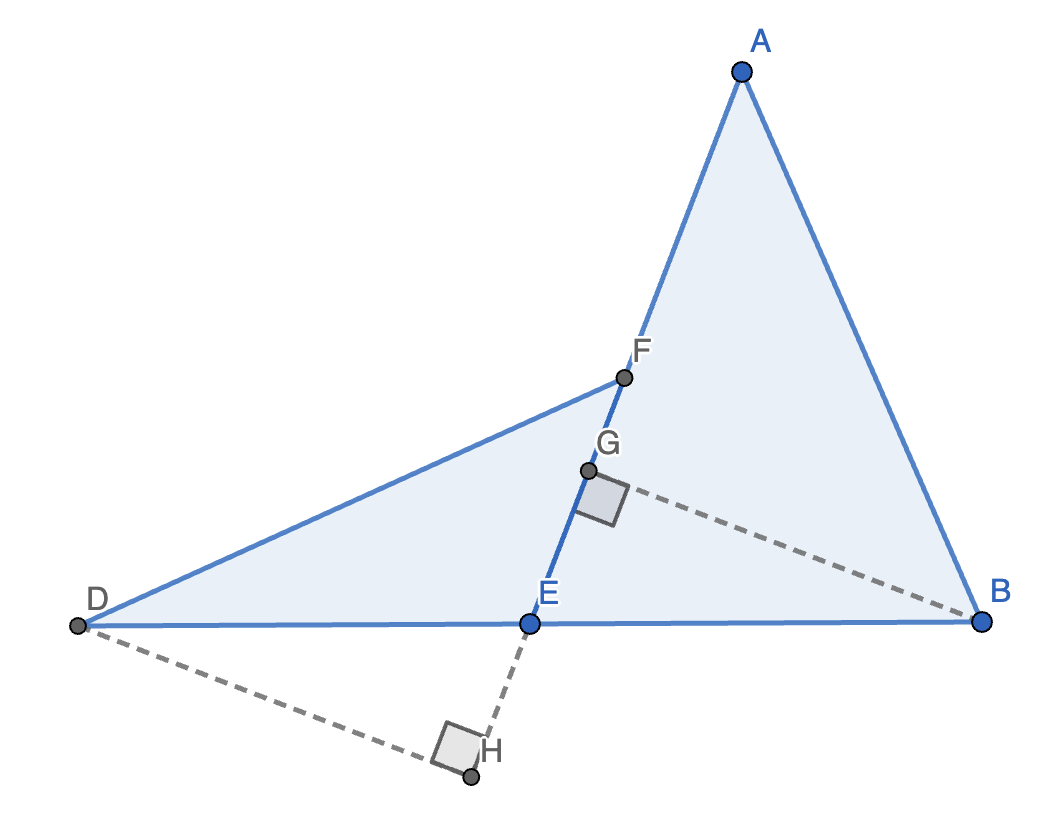
12. 如图，在 $\triangle ABC$ 中，点 $D$ 是 $BC$ 的中点，$DE \perp AC$ 于点 $E$，$DF \perp AB$ 于点 $F$，$BE = CF$。求证：$AB = AC$。

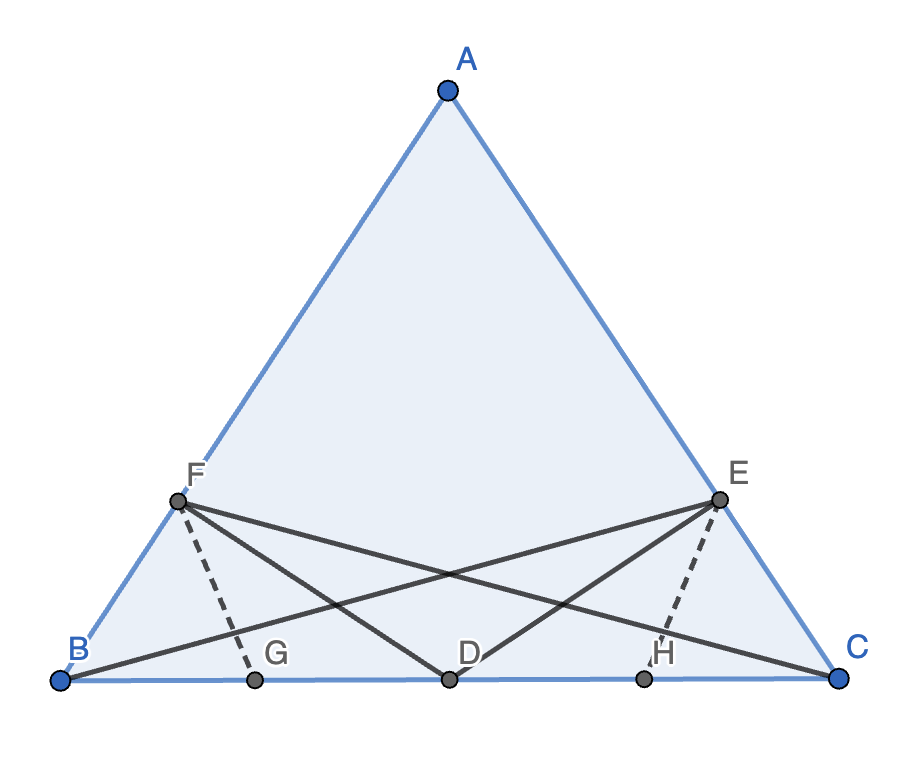
思路：本题的条件中并没有很多角度关系，但有边的关系，所以考虑转换边的位置。再看条件，发现两个直角三角形，所以可以做中线，构造 SSS 全等。

证明：作 $BD$ 的中点 $G$，$CD$ 的中点 $H$，连接 $FG, EH$。

因为 $DE \perp AC, DF \perp AB$，所以 $DG = FG, DH = EH$，所以 $DG = DH = \dfrac{BC}{4}$。

又因为 $BE = CF, BH = CG = \dfrac{3}{4} BC$，所以 $\triangle CFG \cong \triangle BEH \implies \angle CBE = \angle BCF$。

此时可以发现，$\triangle BCE \cong CBF \implies \angle ABC = \angle ABC \implies AB = AC$。

故原命题成立。

13. 如图，在 $\triangle ABC$ 中，$\angle BAC = 100 \degree$，$\angle ABC = 50 \degree$，延长 $AC$ 至 $D$，使得 $CD = AB$，连接 $BD$，求 $\angle D$ 的度数。

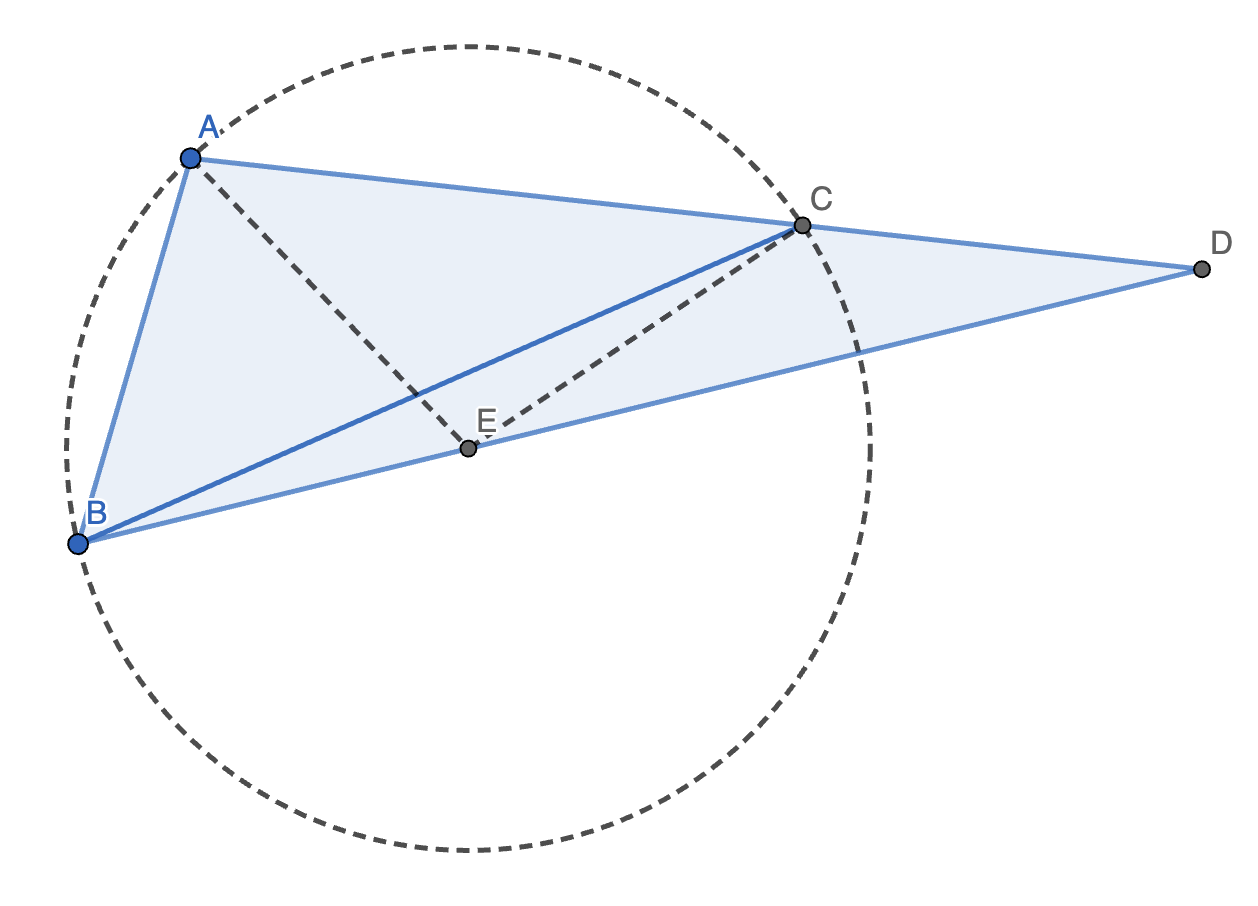
正解：作 $\triangle ABC$ 的外接圆 $\odot E$，连接 $AE, CE$。

可以发现，$\angle AEB = 2 \angle ACB = 60 \degree$，所以 $AB = AE = BE = CD = CE \implies \angle BAE = 60 \degree \implies \angle CAE = \angle ACE = 40 \degree \implies \angle DCE = 140 \degree \implies \angle D = 20 \degree$。

14. 如图，在 $\triangle ABC$ 中，$\angle ACB = 90 \degree$，$\angle ABC = 30 \degree$，点 $D, E$ 分别在 $BC, AC$ 上，$\angle BAD = 40 \degree$，$\angle ABE = 20 \degree$，求 $\angle ADE$ 的度数。

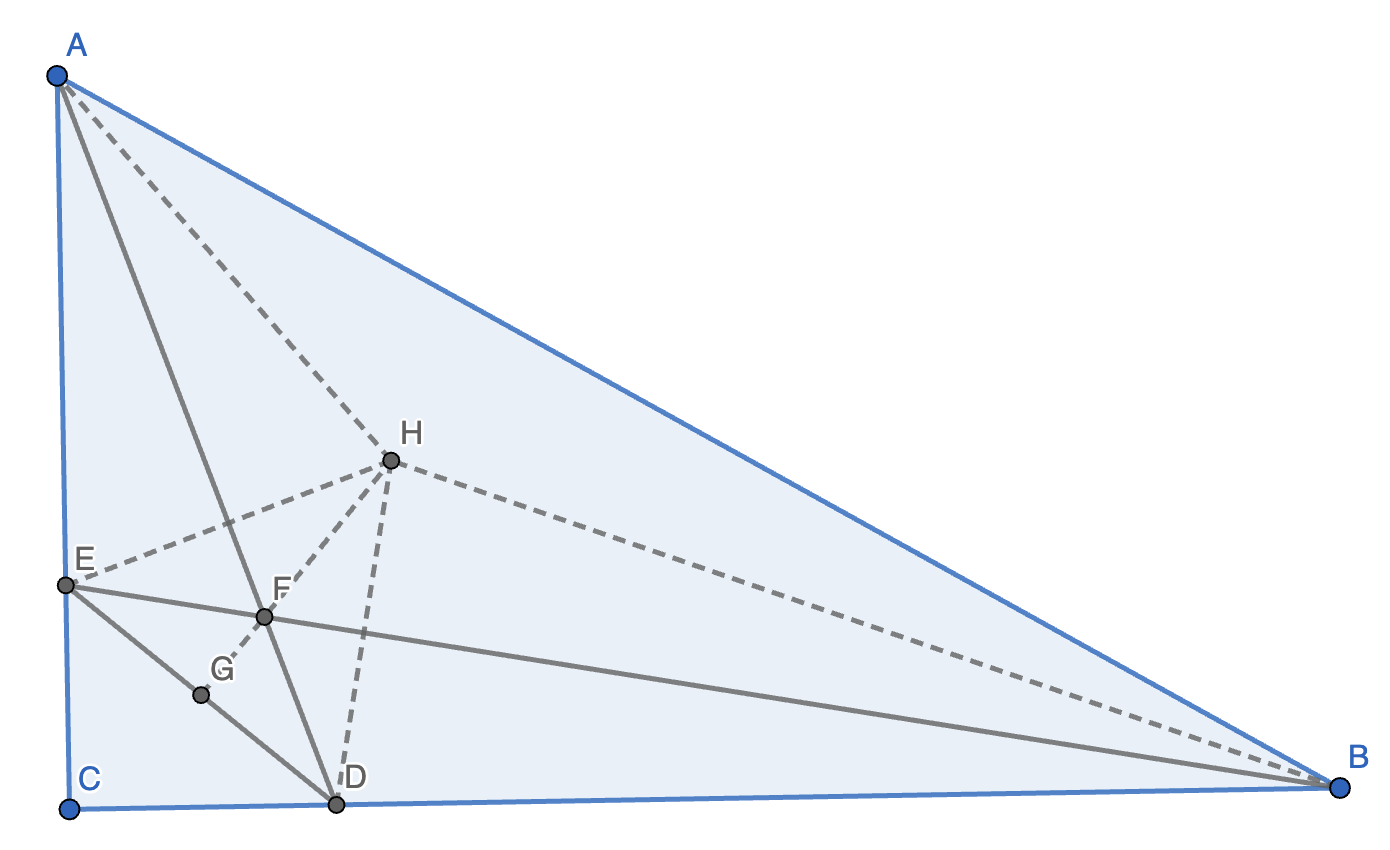
正解：设 $\angle ABE, \angle AEB, \angle BAE$ 的角平分线交于 $H$，连接 $DH, EH$。

可以发现：

$\triangle AEF \cong \triangle AHF$。

$\triangle BDH \cong \triangle BFH$。

$\angle BFD = \angle BFH = \angle AFH = \angle AEF = \angle EFG = \angle EFG = 60 \degree$。

$AF \perp EH, DH \perp BF$。

故 $\angle ADE = \angle BED = \angle BEH = \angle EHF = \angle DHF = \angle ADH = 30 \degree$。

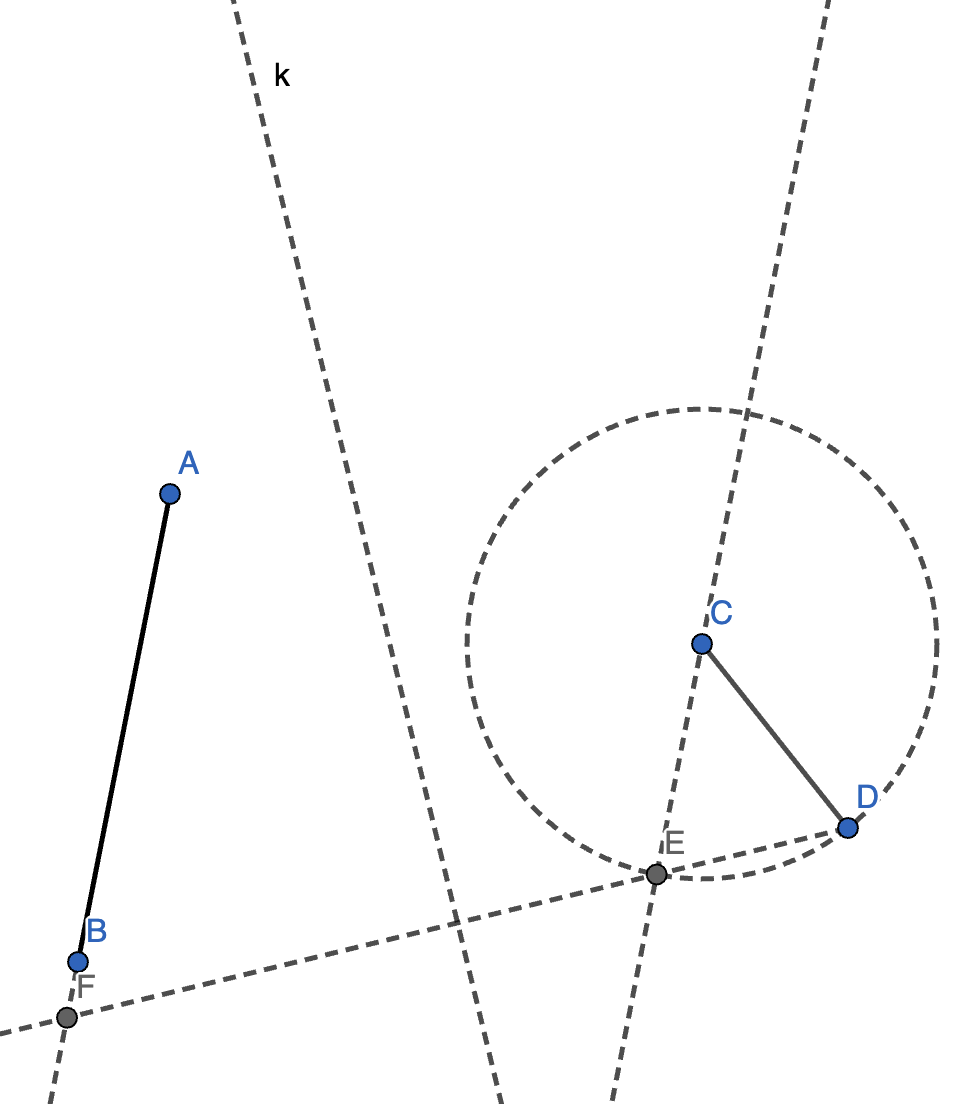
15. 给定两线段 $AB, CD$ 满足 $AB$ 与 $CD$ 相交，求作 $AB, CD$ 所在直线的夹角的角平分线（不能同时延长两线段使得它们相交）。

解法 1（等腰三角形）：

过点 $C$ 作直线 $l \parallel AB$。

以 $C$ 为圆心，$CD$ 为半径作圆，交 $l$ 于点 $E$。

设 $DE$ 交 $AB$ 于点 $F$，连接 $EF$。

作 $DF$ 的中垂线 $k$，即为所求。

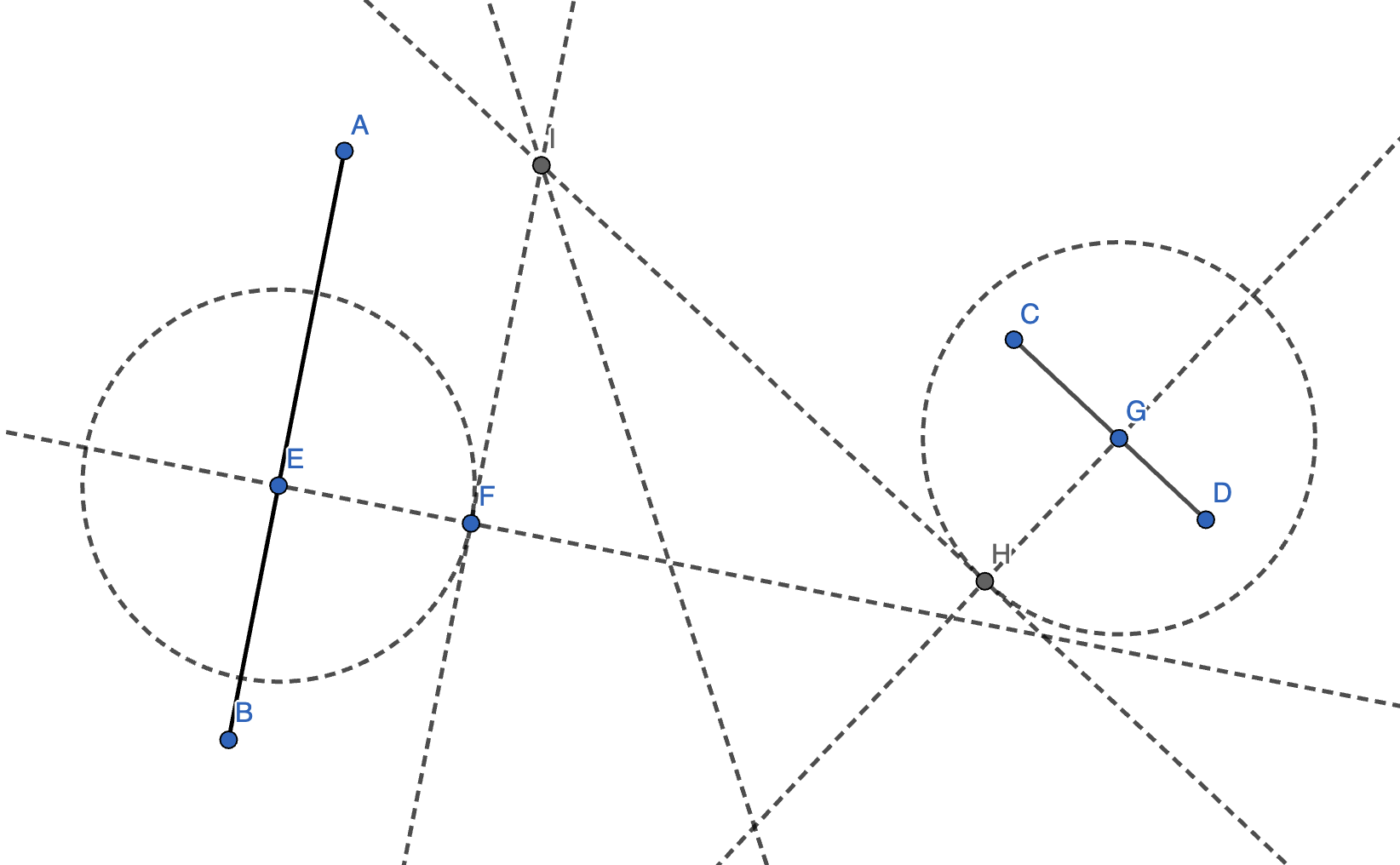
解法 2（平移）：

在 $AB$ 上任取一点 $E$，在 $CD$ 上任取一点 $G$。

以 $E$ 为圆心，合适长度为半径作圆。

过点 $E$ 作直线 $l_1 \perp AB$ 交 $\odot E$ 于点 $F$，过点 $G$ 作直线 $l_2 \perp CD$。

以 $G$ 为圆心，$EF$ 为半径作圆交 $l_2$ 于点 $H$。

分别过点 $F, H$ 作 $m_1 \parallel AB, m_2 \parallel CD$，设 $m_1$ 交 $m_2$ 于点 $I$。

则 $\angle FIH$ 的角平分线即为所求。

解法 3（内心）：

连接 $BD$。

分别作 $\angle ABD, \angle BDC$ 的角平分线，设它们交于点 $E$。

作 $CF \parallel AB$ 交 $BD$ 于点 $F$。

作 $\angle DCF$ 的角平分线 $l$。

过点 $E$ 作 $l$ 的平行线即为所求。

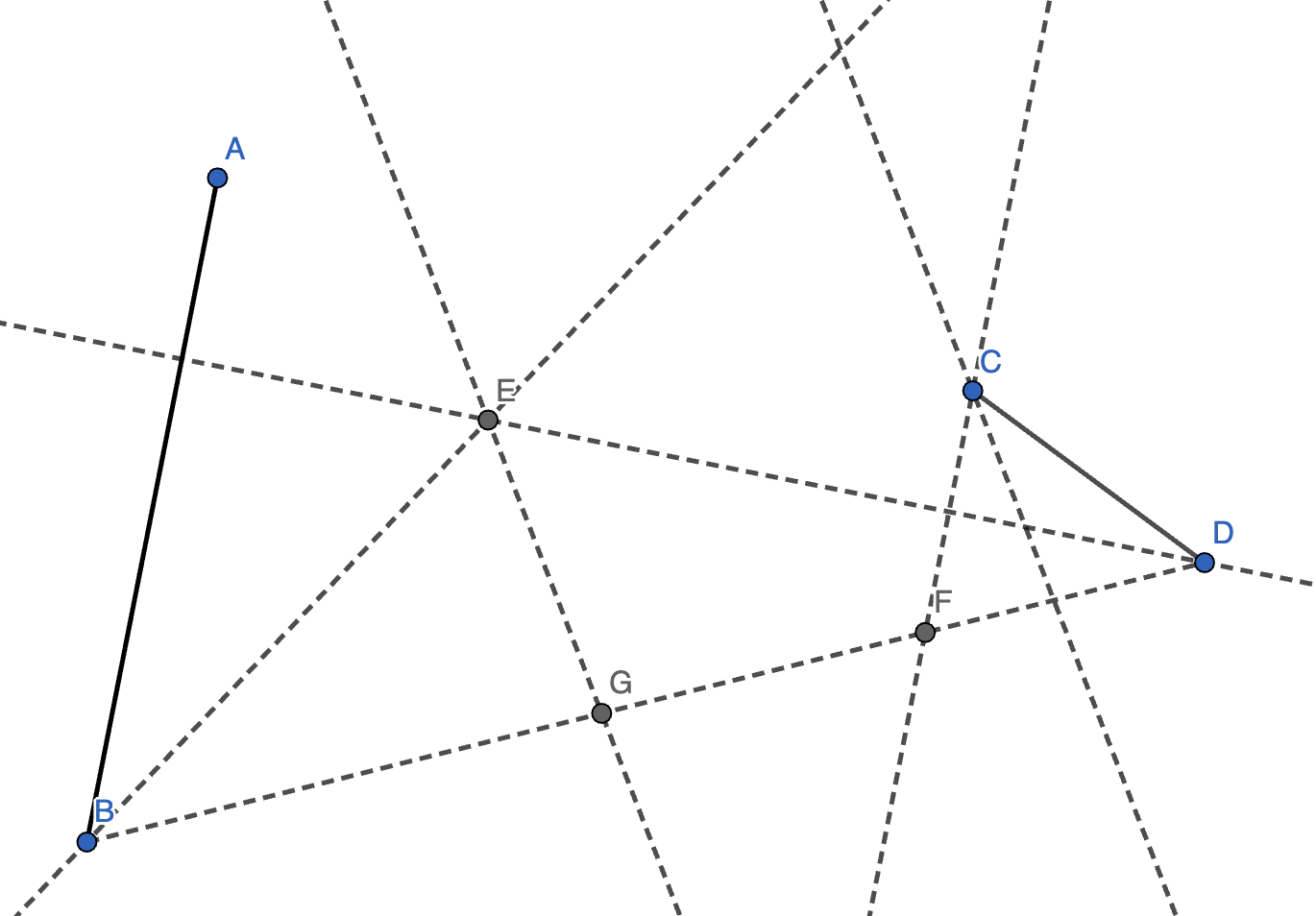
16. 在 $\triangle ABC$ 中，$AD$ 是 $BC$ 边上的高，点 $C'$ 与点 $C$ 关于直线 $AB$ 对称，点 $E$ 是线段 $BC'$ 上的点，且 $AE = AC$。连接 $CE$，作 $DF \perp AB$ 于 $F$ 交 $CE$ 于点 $G$。求证：$CG = EG$。

证明：

如图，连接 $CC'$，作 $AH \perp BC'$，连接 $FH$。（技巧：发现有对称时，可以尝试把对应两点连接。）

因为 $DF \perp AB$，故 $D, F, H$ 三点共线。

因为 $AE = AC = AC', AH \perp BC'$，故 $EH = C'H$。（技巧：既有平行又有中点，所以一定有中位线。）

因为 $BC'^2 - BC^2 = AC'^2 - AC^2 = 0$，故 $AB \perp CC'$。

又因为 $DF \perp AB$，故 $CC' \parallel DH$，故 $DH$ 是 $\triangle CC'E$ 的中位线，故 $CG = EG$。

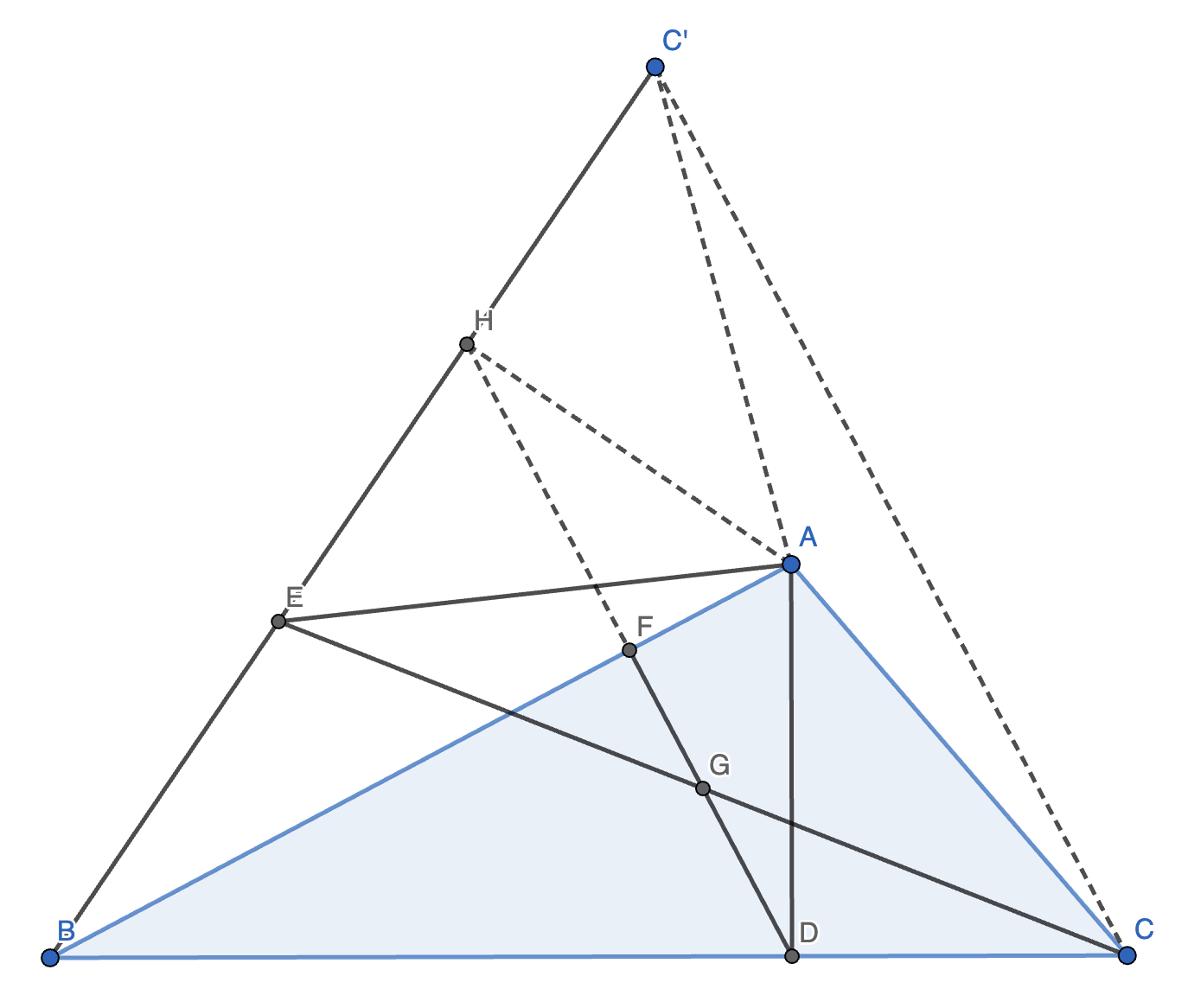
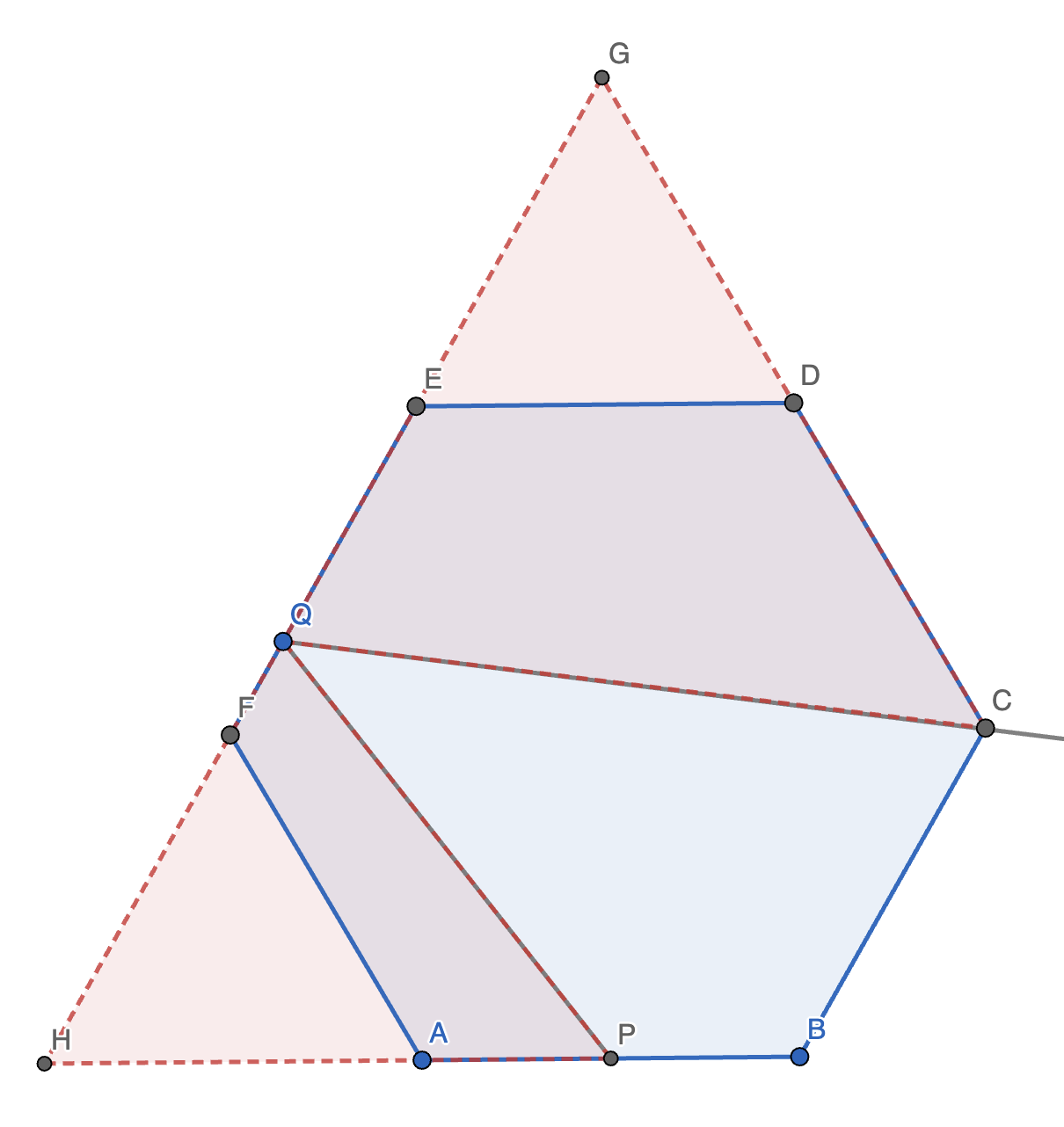
17. 在正六边形 $ABCDEF$ 中，$P$ 为 $AB$ 的中点。光线 $PQ$ 经过边 $EF$ 反射后，恰好经过点 $C$。求 $EQ$ 的值。

解法 1（三角法）：

如图，作 $ABCDEF$ 关于 $EF$ 对称的图形 $\omega$，延长 $AF$ 交 $\omega$ 于 $H$，延长 $PQ$。

因为 $PQ$ 经过边 $EF$ 反射后过点 $C$，故 $PQ$ 延长后过点 $H$。（技巧：遇到光的反射，可以把反射光线进行对称，通常可以发现结论。）

连接 $CH$，显然 $E$ 在 $CH$ 上，且 $CE = CH$，且 $BC \perp CH$。延长 $CB$ 交 $PQ$ 于点 $I$。

因为 $CE = CH, EQ \parallel BC$，故 $EQ$ 为 $\triangle CHI$ 的中位线，故 $EQ = \dfrac{CI}{2}$。

容易发现，$AH = 6, AP = 1$。

根据余弦定理，$HP = \sqrt{AH^2 + AP^2 - 2AH \cdot AP \cos 120 \degree} = \sqrt{43}$。

故 $\cos \angle BPI = \cos \angle APH = \dfrac{AP^2 + HP^2 - AH^2}{2AP \cdot HP} = \dfrac{4}{43} \sqrt{43}$。

故 $\sin \angle BPI = \sqrt{1 - \cos^2 \angle BPI} = \dfrac{3}{43} \sqrt{129}$。

故 $\sin I = \sin(120 \degree - \angle BPI) = \sin 120 \degree \cos \angle BPI - \cos 120 \degree \sin \angle BPI = \dfrac{7}{86} \sqrt{129}$。

故 $\cos I = \sqrt{1 - \sin^2 I} = \dfrac{5}{86} \sqrt{43}$。

故 $CI = \dfrac{\cos I}{\sin I} \cdot CH = \dfrac{\cos I}{\sin I} \cdot 4 \sqrt{3} = \dfrac{20}{7}$。

故 $EQ = \dfrac{CI}{2} = \dfrac{10}{7}$。

解法 2：

如图，作 $ABCDEF$ 关于 $EF$ 对称的图形 $\omega$，延长 $PQ$ 交 $\omega$ 于 $H$。

作 $KQ \perp BC$ 于 $K$，$JP \perp BC$ 于 $J$。（技巧：遇到相等的角，要让它们在一个或两个三角形里，以便于分析。）

容易发现，$\angle JBP = 60 \degree$，且 $\triangle IJP \sim \triangle IKQ$。

故 $JP = \dfrac{1}{2} \sqrt{3}, KQ = 2 \sqrt{3}$，故相似比为 $1 : 4$。

又知 $BJ = \dfrac{1}{2}$，故可列方程组：

\[\begin{cases} IJ + \dfrac{1}{2} + BK = 2 - BK \\ 3IJ = \dfrac{1}{2} + BK \end{cases} \]
解得：$IJ = \dfrac{5}{14}, BK = \dfrac{4}{7}$，故 $CK = 2 - BK = \dfrac{10}{7}$。

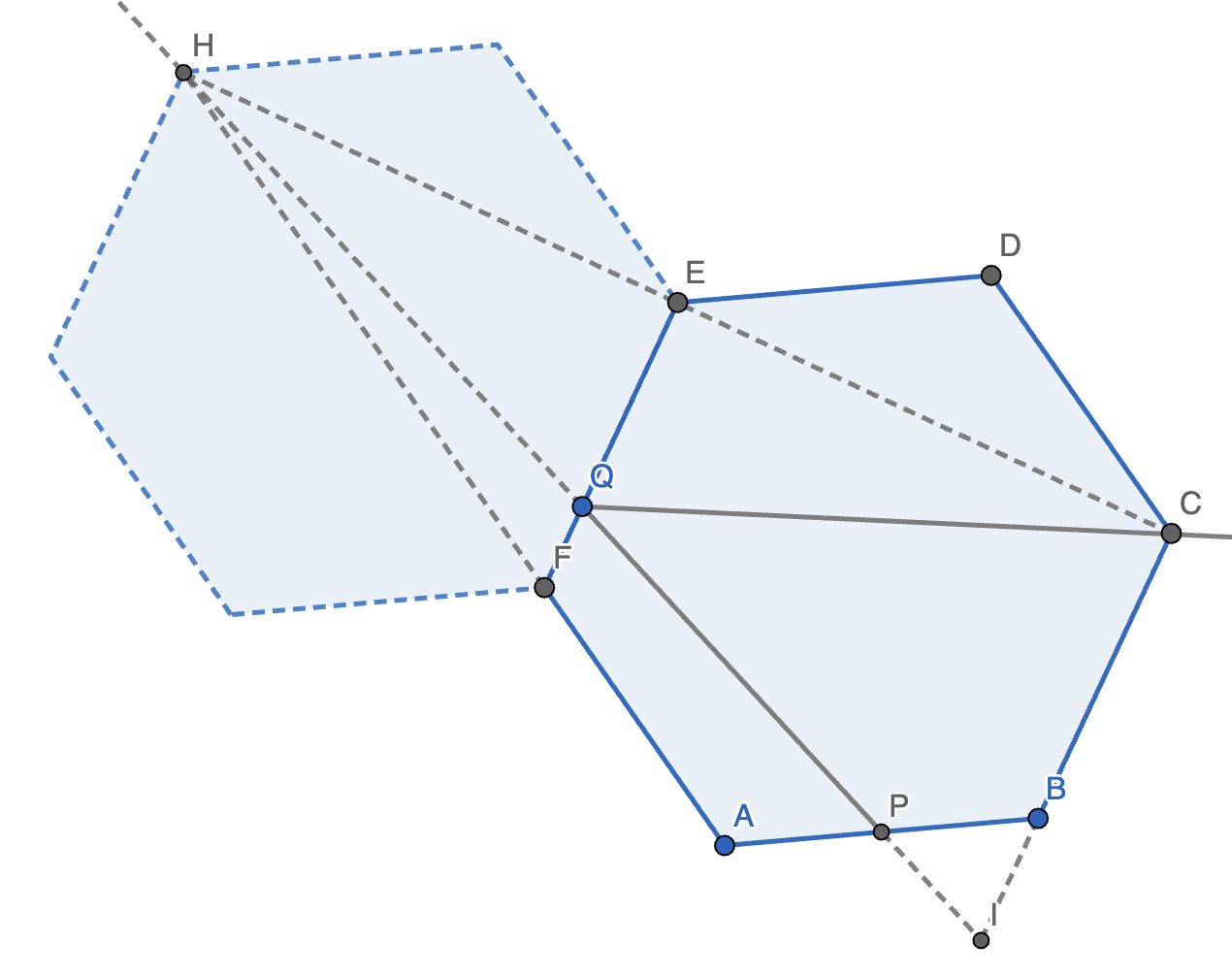
解法 3：

延长 $PA$ 交 $FQ$ 于 $H$，延长 $CD$ 交 $EQ$ 于 $G$。

可以发现，$\angle HQP = \angle CQD, \angle H = \angle G = 60 \degree, CG = 4, HP = 3, \triangle HQP \sim \triangle GQC$。

故 $(2 + EQ) : (4 - EQ) = CG : HP = 4 : 3 \implies EQ = \dfrac{10}{7}$。

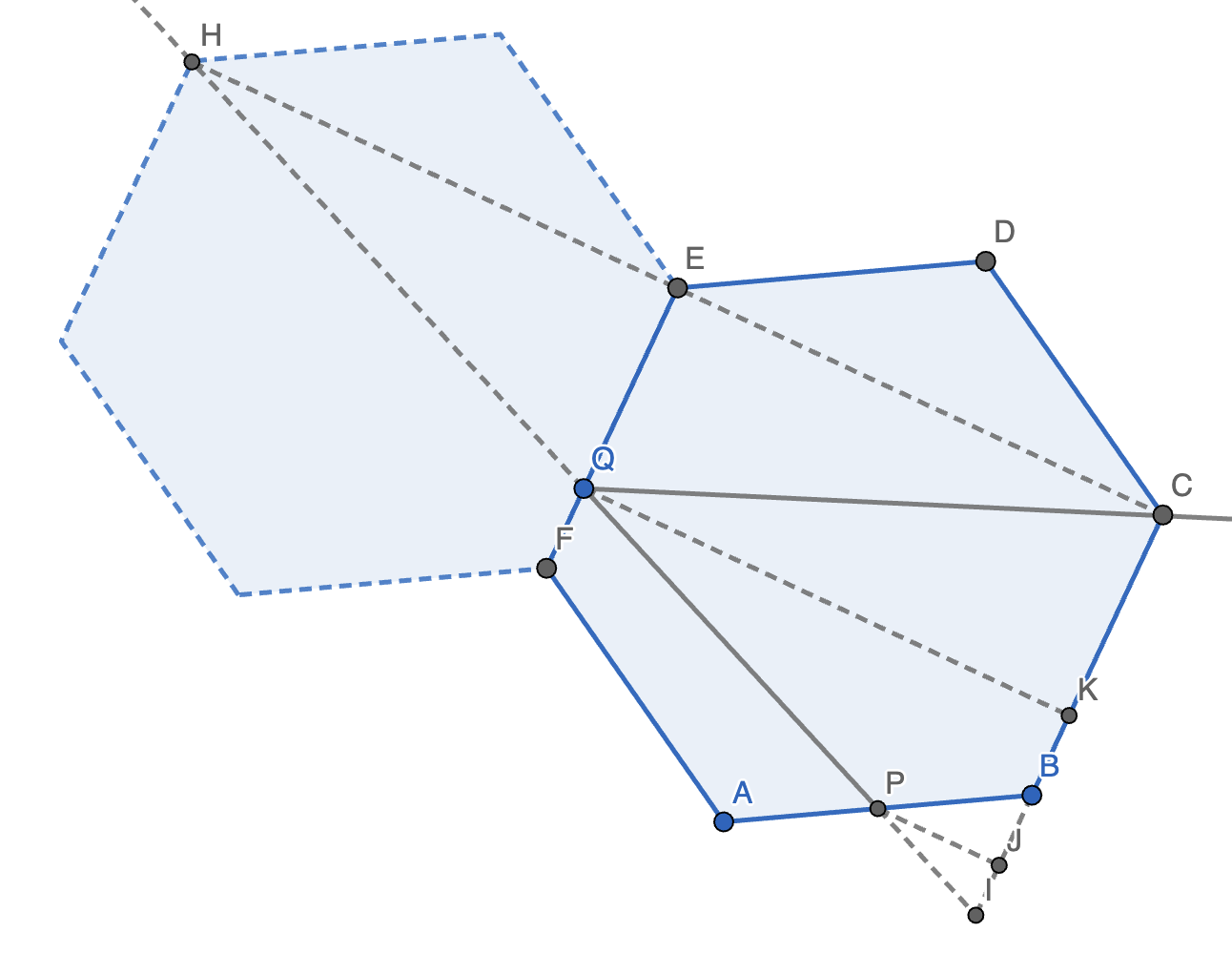
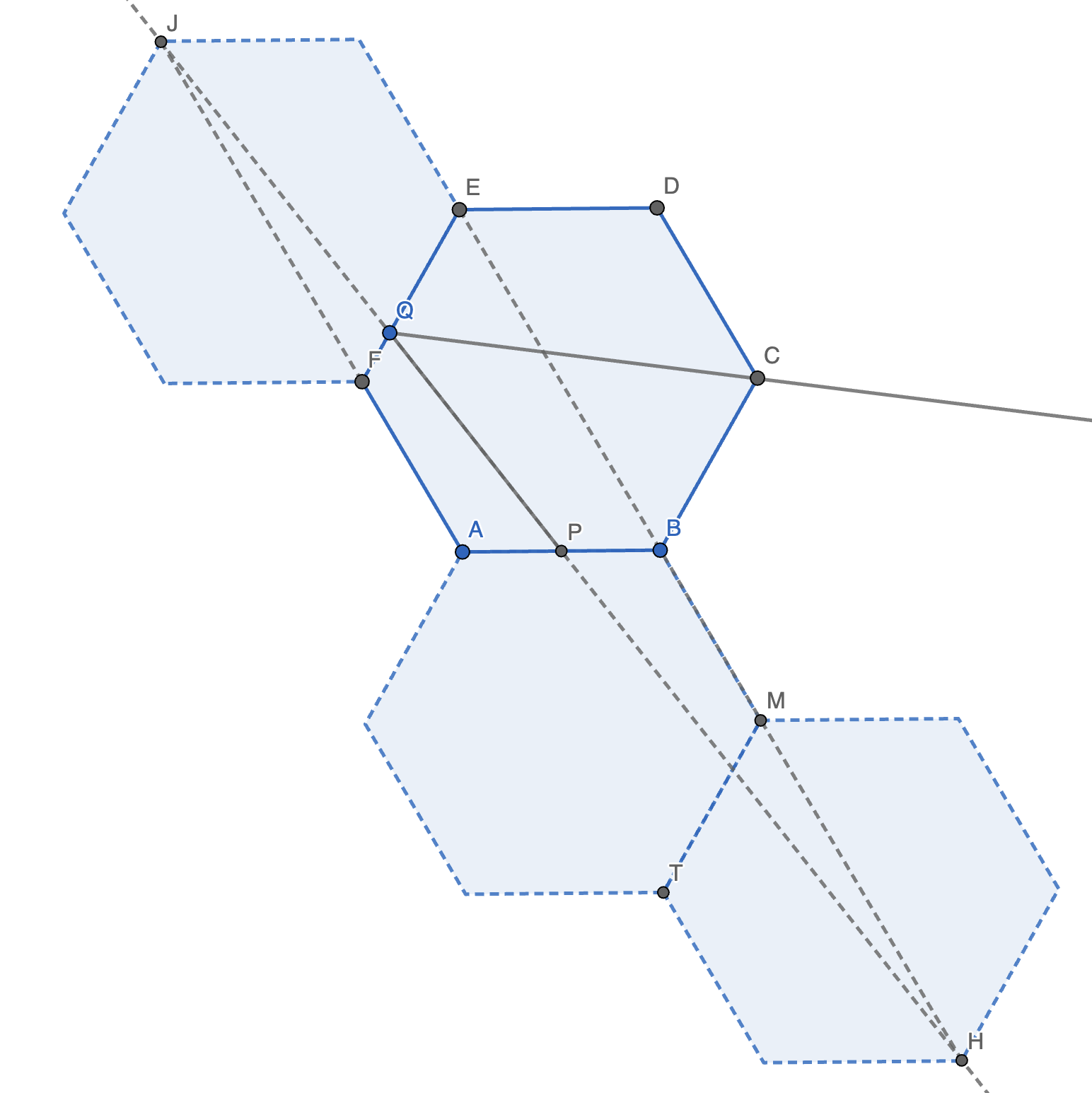
解法 4：

如图，将六边形 $ABCDEF$ 关于 $EF$ 对称得六边形 $\omega_1$，关于 $AB$ 对称得 $\omega_2$。再将 $\omega_2$ 关于 $MT$ 对称得 $\omega_3$。连接并延长 $EB$ 交 $\omega_3$ 于 $H$。延长 $AF$ 交 $\omega_1$ 于 $J$，连接 $JQ$。

注意到，$\angle FQJ = \angle EQH, \angle QFJ = \angle HEQ = 60 \degree$，故 $\triangle FJQ \sim \triangle EHQ$。

故 $EQ : (2 - EQ) = EH : FJ = 10 : 4 = 5 : 2 \implies EQ = \dfrac{10}{7}$。

18.（1995 AIME 第 4 题）已知：

$\odot O$ 的半径为 $9$，$\odot A$ 的半径为 $6$，$\odot B$ 的半径为 $3$。
$\odot A$ 与 $\odot B$ 相切。
$\odot A, \odot B$ 都与 $\odot O$ 内切。
$\odot O$ 上的弦 $XY$ 与 $\odot A, \odot B$ 同时相切，其中点 $Y$ 更靠近 $\odot A$。

求 $XY^2$ 的值。

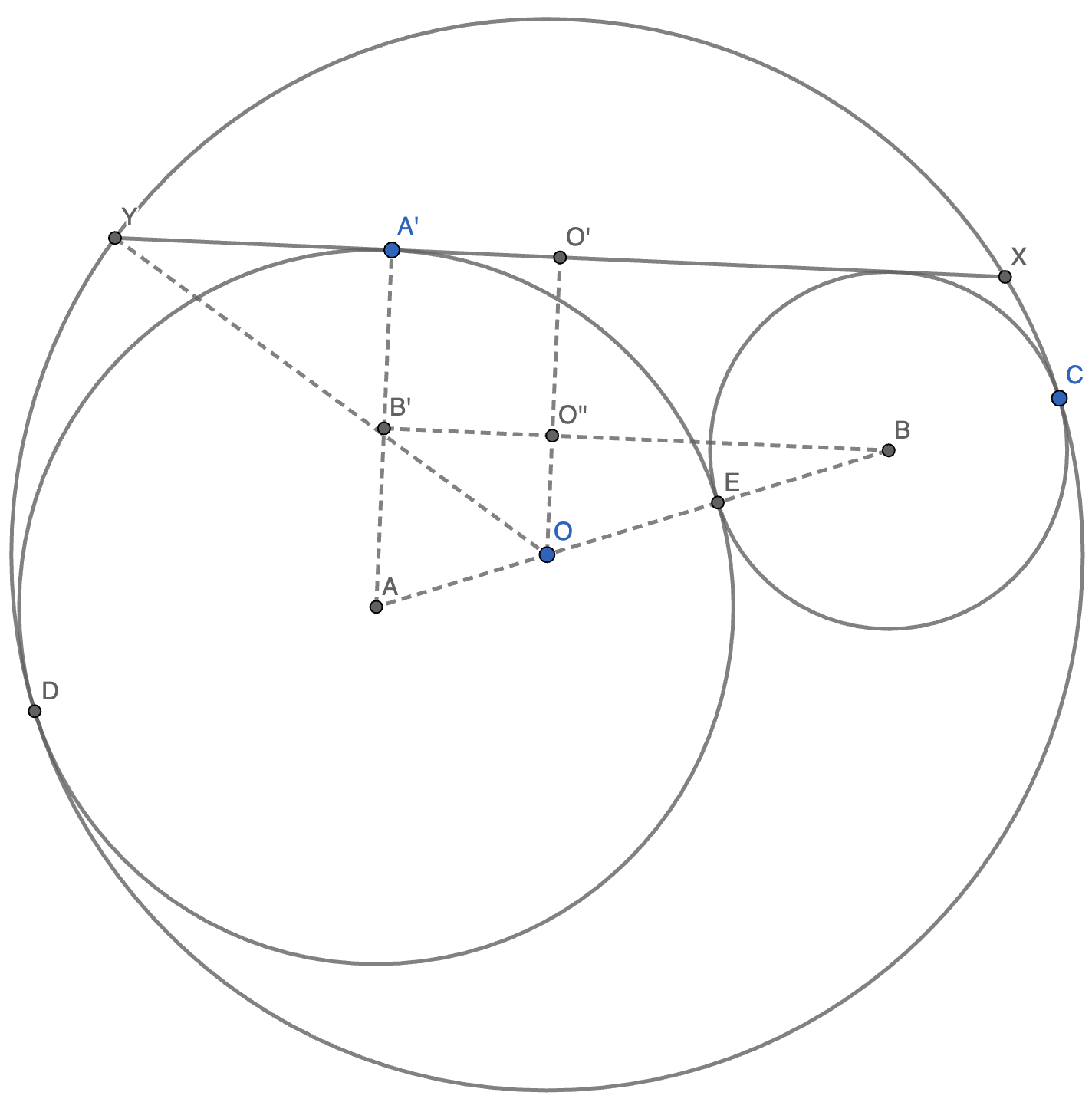
正解：

作 $AA' \perp XY$ 于 $A'$，$OO' \perp XY$ 于 $O'$，$BB' \perp AA'$ 于 $B'$。设 $OO'$ 交 $BB'$ 于 $O''$。

容易发现，$AB' = A'B' = O'O'' = AO = EO = BE = 3$，且 $\triangle BOO' \sim \triangle BAB'$，且相似比为 $BO : AB = 2 : 3$。故 $OO'' = 2 \implies OO' = OO'' + O'O'' = 5$。

又知 $OY = 9$，故 $O'Y^2 = OY^2 - OO'^2 = 9^2 - 5^2 = 56 \implies XY^2 = (2O'Y)^2 = 4O'Y^2 = 224$。

19. $\sin(\alpha), \sin(\beta)$ 是方程 $x^2 - (\sqrt{2} \cos(20 \degree)) x + \left( \cos^2(20 \degree) - \dfrac{1}{2} \right) = 0$ 的两根，其中 $0 < \alpha, \beta < \pi / 2, \alpha > \beta$，求 $\alpha, \beta$ 的值。

正解：根据韦达定理：

\[\begin{cases} \sin(\alpha) + \sin(\beta) = \sqrt{2} \cos(20 \degree) \\ \sin(\alpha) \sin(\beta) = \cos^2(20 \degree) - \dfrac{1}{2} \end{cases} \]
对第一个式子逆用辅助角公式：

\[\begin{aligned} \sin(\alpha) + \sin(\beta) &= \sqrt{2} \cos(20 \degree) \\ &= \sqrt{2} \sin(70 \degree) \\ &= \sqrt{2} \sin(25 \degree + 45 \degree) \\ &= \sin(25 \degree) + \cos(25 \degree) \\ &= \sin(25 \degree) + \sin(65 \degree) \end{aligned} \]
第二个式子可以降次：

\[\begin{aligned} \sin(\alpha) \sin(\beta) &= \cos^2(20 \degree) - \dfrac{1}{2} \\ &= \cos^2(20 \degree) - \dfrac{1}{2} \cos^2(20 \degree) - \dfrac{1}{2} \sin^2(20 \degree) \\ &= \dfrac{1}{2} \cos^2(20 \degree) - \dfrac{1}{2} \sin^2(20 \degree) \\ &= \dfrac{1}{2} \cos(40 \degree) \\ &= \dfrac{1}{2} \sin(50 \degree) \\ &= \sin(25 \degree) \cos(25 \degree) \\ \end{aligned} \]
对比左右两边可知 $\alpha = 65 \degree, \beta = 25 \degree$。

20. 若 $\sin(x) + \sin(y) + \sin(z) = \cos(x) + \cos(y) + \cos(z) = 0$，求 $\cos(x - y)$。

正解：则 $\sin(x) + \sin(y) = -\sin(z), \cos(x) + \cos(y) = -\cos(z)$。

则：

\[\begin{aligned} (\sin(x) + \sin(y))^2 + (\cos(x) + \cos(y))^2 &= 2(\cos(x) \cos(y) + \sin(x) \sin(y)) + 2 \\ &= 2 \cos(x - y) + 2 \\ &= 1 \end{aligned} \]
解得 $\cos(x - y) = -\dfrac{1}{2}$。

21. 已知 $a + b = \pi / 12$，求 $\dfrac{1 - \tan(a) - \tan(b) - \tan(a) \tan(b)}{1 + \tan(a) + \tan(b) - \tan(a) \tan(b)}$ 的值。

正解：令 $\tan(a + b) = \dfrac{\tan(a) + \tan(b)}{1 - \tan(a) \tan(b)} = \dfrac{p}{q}$，则原式为 $\dfrac{q - p}{q + p} = \dfrac{1 - p / q}{1 + p / q}$。

易知 $\dfrac{p}{q} = \tan(\pi / 12) = 2 - \sqrt{3}$，则原式为 $\dfrac{\sqrt{3} - 1}{3 - \sqrt{3}} = \dfrac{\sqrt{3}}{3}$。

22. 求 $\cos(\pi / 17) \cos(2 \pi / 17) \cos(4 \pi / 17) \cos(8 \pi / 17)$ 的值。

正解：我们发现只需要乘 $\sin(\pi / 17)$ 就有二倍角公式。

设 $A$ 为原式，$B = 2^4 \sin(\pi / 17)$，则 $AB = \sin(16 \pi / 17)$，则 $A = \dfrac{\sin(16 \pi / 17)}{B} = \dfrac{\sin(16 \pi / 17)}{16 \sin(\pi / 17)} = \dfrac{1}{16}$。

评注：这道题和以下题目很相似：化简 $(1 + x)(1 + x^2)(1 + x^4) \cdots (1 + x^{256})$。

23. 已知 $5 \sin(\alpha + \beta) + 3 \sin(\alpha) = 0$，求 $\tan \left( \alpha + \dfrac{\beta}{2} \right) \cot \left( \dfrac{\beta}{2} \right)$ 的值。

正解：注意到，$\left( \alpha + \dfrac{\beta}{2} \right) + \dfrac{\beta}{2} = \alpha + \beta, \left( \alpha + \dfrac{\beta}{2} \right) - \dfrac{\beta}{2} = \alpha$。（技巧：要让条件和结论尽量接近。）

则设 $x = \alpha + \dfrac{\beta}{2}, y = \dfrac{\beta}{2}$，则 $5 \sin(x + y) + 3 \sin(x - y) = 8 \sin(x) \cos(y) + 2 \sin(y) \cos(x) = 0$，且 $\tan \left( \alpha + \dfrac{\beta}{2} \right) \cot \left( \dfrac{\beta}{2} \right) = \tan(x) \cot(y)$。

则 $4 \sin(x) \cos(y) = -\sin(y) \cos(x) \implies \dfrac{\sin(x) \cos(y)}{\sin(y) \cos(x)} = \dfrac{\sin(x)}{\cos(x)} \cdot \dfrac{\cos(y)}{\sin(y)} = \tan(x) \cot(y) = -\dfrac{1}{4}$。

24. $\triangle ABC$ 满足 $b = 2, B = 45 \degree$，若存在两个 $\triangle ABC$，求 $a$ 的取值范围。

解法 1（建系法）：因为 $B = 45 \degree$，所以设 $BC$ 边在 $y = x$ 上，$AB$ 边在 $x$ 轴上，则可知 $C \left( \dfrac{\sqrt{2}}{2} a, \dfrac{\sqrt{2}}{2} a \right)$。

以 $C$ 为圆心，$b = 2$ 为半径作圆 $\omega$，则 $\omega$ 与 $x$ 轴有 2 个交点，且都在正半轴上。

容易发现，$\omega : \left( x - \dfrac{\sqrt{2}}{2} a \right)^2 + \left( y - \dfrac{\sqrt{2}}{2} a \right)^2 = 4$，则交点 $A$ 满足：

\[\left( x_A - \dfrac{\sqrt{2}}{2} a \right)^2 + \left( 0 - \dfrac{\sqrt{2}}{2} a \right)^2 = 4 \]
即：

\[x_A^2 - \sqrt{2} ax_A + (a^2 - 4) = 0 \]
则该方程有 2 个正根，故：

\[\begin{cases} \Delta = 2a^2 - 4(a^2 - 4) = 16 - 2a^2 > 0 \\ \sqrt{2} a > 0 \\ a^2 - 4 > 0 \end{cases} \]
解得 $a \in (2, 2 \sqrt{2})$。

解法 2（余弦定理）：由余弦定理可知 $b^2 = a^2 + c^2 - 2ac \cos(B)$，即 $a^2 + c^2 - \sqrt{2} ac = 4$。

将它看作关于 $c$ 的二次方程，则它有 2 个正实根，则有：

\[\begin{cases} \Delta = 2a^2 - 4(a^2 - 4) = 16 - 2a^2 > 0 \\ \sqrt{2} a > 0 \\ a^2 - 4 > 0 \end{cases} \]
解得 $a \in (2, 2 \sqrt{2})$。

25. 在 $\triangle ABC$ 中有 $a^2 + 2b^2 + 3c^2 = 12$，求 $\max(S_{\triangle ABC})$。

正解：先消元：

\[a^2 = 12 - 2b^2 - 3c^2 \]
然后使用海伦公式：（技巧：条件只有边的关系，所以用边计算面积。）

\[\begin{aligned} S_{\triangle ABC} &= \dfrac{1}{4} \sqrt{(a + b + c)(a + b - c)(b + c - a)(c + a - b)} \\ &= \dfrac{1}{4} \sqrt{((b + c)^2 - a^2)(a^2 - (b - c)^2)} \\ &= \dfrac{1}{4} \sqrt{(b^2 + 2bc + c^2 - a^2)(a^2 - b^2 + 2bc - c^2)} \\ &= \dfrac{1}{4} \sqrt{(2bc + 3b^2 + 4c^2 - 12)(2bc - 3b^2 - 4c^2 + 12)} \\ &= \dfrac{1}{4} \sqrt{4b^2 c^2 - (3b^2 + 4c^2 - 12)^2} \\ \end{aligned} \]
注意到，$3b^2 + 4c^2 - 12 \ge 4 \sqrt{3} bc - 12 \ge 0$。

证明（?）：因为 $4 \sqrt{3} bc - 12 \ge 0 \iff bc \ge \sqrt{3}$，所以只需证明在 $bc < \sqrt{3}$ 时 $S_{\triangle ABC}$ 不是最大值。

因为 $\sin(A) \le 1$，所以此时 $S_{\triangle ABC} = \dfrac{1}{2} bc \sin(A) < \dfrac{1}{2} \sqrt{3} < \dfrac{3 \sqrt{11}}{11}$，不是最大值。

则：

\[\begin{aligned} S_{\triangle ABC} &= \dfrac{1}{4} \sqrt{4b^2 c^2 - (3b^2 + 4c^2 - 12)^2} \\ &\le \dfrac{1}{4} \sqrt{4b^2 c^2 - \left( 4 \sqrt{3} bc - 12 \right)^2} \\ &= \dfrac{1}{4} \sqrt{-44b^2 c^2 + 96 \sqrt{3} bc - 144} \\ \end{aligned} \]
因为 $\max \left( -44x^2 + 96 \sqrt{3} x - 144 \right) = \dfrac{144}{11}$，所以 $\max(S_{\triangle ABC}) = \dfrac{1}{4} \sqrt{\dfrac{144}{11}} = \dfrac{3 \sqrt{11}}{11}$。

26. 已知 $x, y \in (0, \pi)$，且 $\cos(x) + \cos(y) - \cos(x + y) = \dfrac{3}{2}$，求 $x, y$ 的值。

正解：

\[\begin{aligned} \cos(x) + \cos(y) - \cos(x + y) &= 2 \cos \left( \dfrac{x + y}{2} \right) \cos \left( \dfrac{x - y}{2} \right) - \cos(x + y) \\ &= 2 \cos \left( \dfrac{x + y}{2} \right) \cos \left( \dfrac{x - y}{2} \right) - 2 \cos^2 \left( \dfrac{x + y}{2} \right) + 1 \\ &= \dfrac{3}{2} \end{aligned} \]
设 $a = \cos \left( \dfrac{x + y}{2} \right), b = \cos \left( \dfrac{x - y}{2} \right)$，则 $-2a^2 + 2ab - \dfrac{1}{2} = 0$。

主元 $a$，则该方程有解，则 $\Delta = 4b^2 - 4 \ge 0 \iff b = \pm 1$。

在 $b = -1$ 时，$\dfrac{x - y}{2} = \pi \iff x - y = 2 \pi \implies x > 2 \pi$，与题目条件矛盾。

故 $b = 1$，$\dfrac{x - y}{2} = 0 \iff x = y$，则 $2 \cos(x) - \cos(2x) = 2 \cos(x) - 2 \cos^2(x) + 1 = \dfrac{3}{2} \iff \cos(x) = \cos(y) = \dfrac{1}{2} \iff x = y = \dfrac{1}{3} \pi$。

27. 设 $\vec{a}, \vec{b} \neq \vec{0}$ 满足 $\vec{a} + 3 \vec{b} \perp 7 \vec{a} - 5 \vec{b}$ 且 $\vec{a} - 4 \vec{b} \perp 7 \vec{a} - 2 \vec{b}$，求 $\vec{a}$ 与 $\vec{b}$ 的夹角的度数。

解法 1（建系法）：设 $\vec{a} = (x_1, y_1)$，则 $\vec{b} = \left( -\dfrac{x_1}{3}, y_2 \right)$，则：

$\vec{a} - 4 \vec{b} = \left( \dfrac{7}{3} x_1, y_1 - 4y_2 \right) = (A, B)$。

$7 \vec{a} - 2 \vec{b} = \left( \dfrac{23}{3} x_1, 7y_1 - 2y_2 \right) = (C, D)$。

$\vec{a} + 3 \vec{b} = (0, y_1 + 3y_2)$。

$7 \vec{a} - 5 \vec{b} = \left( \dfrac{26}{3} x_1, 7y_1 - 5y_2 \right)$。

设 $E(A, B), F(C, D)$，则原点在以 $EF$ 为直径的圆上。

该圆的方程为：

\[\left( x - \dfrac{A + C}{2} \right)^2 + \left( y - \dfrac{B + D}{2} \right)^2 = \dfrac{(C - A)^2 + (D - B)^2}{4} \]
即：

\[(x - 5 x_1)^2 + (y - 4 y_1 + 3y_2)^2 = \dfrac{1}{4} (6y_1 + 2y_2)^2 + \left( \dfrac{1}{3} x_1 \right)^2 \tag{1} \]
同理可得：

\[\left( x - \dfrac{1}{2} y_1 - \dfrac{3}{2} y_2 \right)^2 + \left( y - \dfrac{13}{3} x_1 - \dfrac{7}{2} y_1 + \dfrac{5}{2} y_2 \right)^2 = (3y_1 - 4y_2)^2 + \left( \dfrac{13}{3} x_1 \right)^2 \tag{2} \]
由题目条件可得 $x = y = 0$ 为方程 $(1)$、$(2)$ 的公共解。

代入 $x = y = 0$ 于 $(1)$、$(2)$，解得：

\[\begin{cases} x_1 = \pm \dfrac{3 \sqrt{5}}{5} y_1 \\ y_2 = \dfrac{7}{5} y_1 \end{cases} \tag{3} \]
设 $\vec{a}$ 与 $\vec{b}$ 的夹角为 $\theta$，则：

\[\cos(\pi - \theta) = -\cos(\theta) = \dfrac{2x_1^2 + y_1^2 + 9y_2^2 - (y_2 + 3y_2)^2}{2 \sqrt{x_1^2 + 9y_2^2} \sqrt{x_1^2 + y_1^2}} \]
代入 $(3)$，得 $\cos(\theta) = \dfrac{1}{2} \iff \theta = 60 \degree$。

28. 设平面向量 $\vec{a}, \vec{b}$ 满足 $|\vec{a} + \vec{b}| = 3, |\vec{a} - 2 \vec{b}| = 1$，求 $\max(\vec{a} \cdot \vec{b})$ 的值。

正解：设 $\vec{u} = \vec{a} + \vec{b}, \vec{v} = \vec{a} - 2 \vec{b}$，则 $\vec{a} \cdot \vec{b} = \dfrac{2 \vec{u} + \vec{v}}{3} \cdot \dfrac{\vec{u} - \vec{v}}{3} = \dfrac{17 - \vec{u} \cdot \vec{v}}{9}$。（评注：条件难以处理，那就换元让它容易处理。）

设 $\vec{u}$ 和 $\vec{v}$ 的夹角为 $\theta$，则 $\vec{a} \cdot \vec{b} = \dfrac{17 - 3 \cos(\theta)}{9}$，则 $\max(\vec{a} \cdot \vec{b}) = \dfrac{17 - 3 \min(\cos(\theta))}{9} = \dfrac{20}{9}$。

29. 在 $\triangle ABC$ 中，已知 $\vec{AB} \cdot \vec{AC} + 2 \vec{BA} \cdot \vec{BC} = 3 \vec{CA} \cdot \vec{CB}$，求 $\max(\sin(C))$ 的值。

正解：发现：（评注：6 个向量太多了，实际上只需要 2 个。因为最后要求 $\sin(C)$，所以保留 $\vec{CA}, \vec{CB}$。）

$\vec{AB} = \vec{CB} - \vec{CA}$。

$\vec{AC} = -\vec{CA}$。

$\vec{BA} = \vec{CA} - \vec{CB}$。

$\vec{BC} = -\vec{CB}$。

则：

\[\vec{CA} \cdot (\vec{CA} - \vec{CB}) + 2 \vec{CB} \cdot (\vec{CB} - \vec{CA}) = 3 \vec{CA} \cdot \vec{CB} \]
即：

\[b^2 + 2a^2 = 6ab \cos(C) \]
代入 $\cos(C) = \dfrac{a^2 + b^2 - c^2}{2ab}$ 得：

\[a^2 + 2b^2 = 3c^2 \]
则：

\[\cos(C) = \dfrac{a^2 + b^2 - c^2}{2ab} = \dfrac{\frac{2}{3} a^2 + \frac{1}{3} b^2}{2ab} \ge \dfrac{\frac{2}{3} \sqrt{2} ab}{2ab} = \dfrac{1}{3} \sqrt{2} \]
注意到 $b^2 + 2a^2 = 6ab \cos(C) > 0$，所以 $\cos(C) > 0$，所以 $\max(\sin(C)) = \sqrt{1 - \min(\cos^2(C))} = \dfrac{\sqrt{7}}{3}$。

30. 在 $\triangle ABC$ 中，$M$ 平分 $BC$，$N$ 平分 $BM$，$A = \dfrac{\pi}{3}$，$S_{\triangle ABC} = \sqrt{3}$，求 $\min(\vec{AM} \cdot \vec{AN})$ 的值。

正解：共线定理得 $\vec{AM} = \dfrac{1}{2} \vec{AB} + \dfrac{1}{2} \vec{AC}, \vec{AN} = \dfrac{3}{4} \vec{AB} + \dfrac{1}{4} \vec{AC}$。（评注：因为 $\vec{AB}$ 和 $\vec{AC}$ 的夹角已知，所以作如此转化。）

则：

\[\begin{aligned} \vec{AM} \cdot \vec{AN} &= \left( \dfrac{1}{2} \vec{AB} + \dfrac{1}{2} \vec{AC} \right) \cdot \left( \dfrac{3}{4} \vec{AB} + \dfrac{1}{4} \vec{AC} \right) \\ &= \dfrac{3}{8} |\vec{AB}|^2 + \dfrac{1}{8} |\vec{AC}|^2 + \dfrac{1}{2} (\vec{AB} \cdot \vec{AC}) \\ &= \dfrac{3}{8} c^2 + \dfrac{1}{8} b^2 + \dfrac{1}{4} bc \end{aligned} \]
又知 $S_{\triangle ABC} = \dfrac{1}{2} bc \sin(A) = \dfrac{\sqrt{3}}{4} bc = \sqrt{3}$，所以 $bc = 4$，所以 $\vec{AM} \cdot \vec{AN} = \dfrac{3}{8} c^2 + \dfrac{1}{8} b^2 + 1 \ge \sqrt{3} + 1$，所以 $\min(\vec{AM} \cdot \vec{AN}) = \sqrt{3} + 1$。

31. 点 $O$ 为 $\triangle ABC$ 外接圆的圆心，且 $AB = 3, AC = 4$。存在 $x \neq 0$，使得 $\vec{AO} = x \cdot \vec{AB} + (1 - 2x) \cdot \vec{AC}$，求 $\cos(\angle BAC)$ 的值。

32. 已知椭圆 $\Omega : \dfrac{x^2}{4} + \dfrac{y^2}{2} = 1$，设 $t > \sqrt{2}$，过 $(0, t)$ 的直线 $l$ 与 $\Omega$ 交于 $A, B$，点 $C(0, 1)$，连接 $AC$ 交 $\Omega$ 于 $D$。若直线 $BD$ 的斜率为 $0$，求 $t$。

正解：因为 $k_{BD} = 0$，所以设 $y_B = y_D = c \in \left[ -\sqrt{2}, \sqrt{2} \right], T = (0, t)$。

则 $|x_B| = |x_D| = \sqrt{4 - 2 c^2}$。容易发现，$x_B, x_D$ 异号，不妨设 $x_B > 0$，则 $x_B = \sqrt{4 - 2 c^2}, x_D = -\sqrt{4 - 2 c^2}$。

则 $A$ 满足：

\[\begin{cases} y_A = \dfrac{1 - c}{\sqrt{4 - 2 c^2}} x_A + 1 \\ \dfrac{1}{4} x_A^2 + \dfrac{1}{2} y_A^2 = 1 \end{cases} \]
则：

\[\begin{cases} x_A = \dfrac{\sqrt{4 - 2c^2}}{3 - 2c} \\ y_A = \dfrac{4 - 3c}{3 - 2c} \end{cases} \]
则：

\[\begin{aligned} t &= c - \dfrac{c - y_A}{\sqrt{4 - 2c^2} - x_A} \sqrt{4 - 2 c^2} \\ &= c - \dfrac{c - \dfrac{4 - 3c}{3 - 2c}}{\sqrt{4 - 2c^2} - \dfrac{\sqrt{4 - 2c^2}}{3 - 2c}} \sqrt{4 - 2 c^2} \\ &= c - \dfrac{(3 - 2c) c - (4 - 3c)}{(3 - 2c) - 1} \\ &= c - \dfrac{-2c^2 + 6c - 4}{2 - 2c} \\ &= c - \dfrac{c^2 - 3c + 2}{c - 1} \\ &= c - (c - 2) \\ &= 2 \end{aligned} \]

评注：本题需要找到正确的求解顺序，如果以 $t \to A \to B, D \to k_{BD}$ 的顺序，计算极其复杂，因为 $A, B, D$ 都满足复杂的二次的关系。

所以，我们从 $k_{BD} = 0$ 入手，设 $y_B = y_D = c$，以：

\[\begin{CD} C @>D>> A @>>> t \\ @.@AAA \\ @.B \end{CD} \]
的顺序求出 $t$ 比较快捷。

函数篇

1. 求证：函数 $f(x) = x^4 - 4x - 2$ 在区间 $[-1, 2]$ 上至少有两个实根。

证明：注意到 $f(-1) = 3, f(0) = -2, f(2) = 6$。则根据零点存在性定理，$f$ 在区间 $[-1, 0], [0, 2]$ 上各有至少一个实根，故总共至少有两个实根。

2. 讨论函数 $f(x) = \dfrac{1}{3} x^3 - x^2 - 2x + 1$ 与 $g(x) = x - a$ 的图像公共点的个数。

解法 1：$f(x)$ 与 $g(x)$ 的公共点与函数 $h(x) = f(x) - g(x) = \dfrac{1}{3} x^3 - x^2 - 3x + 1 + a$ 的零点一一对应。

则原问题等价于：讨论 $F(x) = \dfrac{1}{3} x^3 - x^2 - 3x + 1$ 与 $G(x) = -a$ 的图像公共点的个数。

对 $F$ 求导：$F'(x) = x^2 - 2x - 3 = (x - 3)(x + 1)$。

则其极值为 $(3, -5)$ 和 $\left( -1, \dfrac{5}{3} \right)$。

······

解法 2：······

3. 求函数 $f(x) = \sqrt{x^2 - 2x + 2} + \sqrt{x^2 - 4x + 8}$ 的最小值。

正解：配方得 $f(x) = \sqrt{(x - 1)^2 + 1} + \sqrt{(x - 2)^2 + 4}$。

设 $A(1, 1), B(2, -2), X(x, 0)$，则 $f(x) = AX + BX$。（技巧：见到根号里是平方和，就要想到两点距离公式。）

想要 $f(x)$ 取到最小值，那么 $X$ 在 $AB$ 上，则 $x = \dfrac{4}{3}, \min(f(x)) = f \left( \dfrac{4}{3} \right) = \sqrt{10}$。

4. 设函数 $f(x)$ 满足：

定义域为 $\R$。
$f(x + 1)$ 为奇函数。
$f(x + 2)$ 为偶函数。
当 $x \in [1, 2]$ 时，$f(x) = kx + b$。
$f(0) + f(3) = 8$。

求 $f \left( \dfrac{2021}{2} \right)$ 的值。

正解：容易发现，$f$ 关于 $(1, 0)$ 中心对称、关于 $x = 2$ 轴对称。

则 $f$ 有周期 $T = 4$，则 $f(x) = -f(2 - x) = f(4 - x) = f(x + 4)$。

则 $f(0) = -f(2) = -2k - b, f(3) = f(1) = k + b = 0$。

则 $f(0) + f(3) = -k = 8 \iff k = -8, b = 8$。

因为 $f$ 的周期 $T = 4$，所以 $f \left( \dfrac{2021}{2} \right) = f(2.5) = f(1.5) = -8 \cdot 1.5 + 8 = -4$。

5. 已知函数 $f(x) = e^{x - 1} + x - 2, g(x) = x^2 - ax - a + 3$，设 $f, g$ 的一个零点分别为 $m, n$，满足 $|m - n| \le 1$。求实数 $a$ 的取值范围。

正解：容易发现，$m = 1$。（技巧：遇到超越方程要尝试猜出根。）

则 $0 \le n \le 2$ 且 $n^2 - an - a + 3 = 0$。

即 $a = \dfrac{n^2 + 3}{n + 1} = n + \dfrac{4}{n + 1} - 1$。

因为 $\forall a, \exist 0 \le n \le 2$，所以 $\forall 0 \le n \le 2, \exist a$，所以 $a$ 的取值范围是函数 $h(x) = n + \dfrac{4}{n + 1} - 1$ 在 $[0, 2]$ 上的值域，为 $[2, 3]$。

6. 函数 $f(x)$ 满足：

定义域为 $(-1, 1)$。
对于任意 $x, y$，都有 $f(x) + f(y) = f \left( \dfrac{x + y}{1 + xy} \right)$。
对于任意 $x \le 0$，都有 $f(x) > 0$。
$f(0.5) = -1$。
对于任意 $x \in [-0.5, 0.5], a \in [-1, 1]$，都有 $f(x) \le t^2 - 2at + 1$。

求实数 $t$ 的取值范围。

正解：容易发现，$f$ 既为奇函数，也为减函数。

则在 $x \in [-0.5, 0.5]$ 时有 $f(x) \in [-1, 1]$，且 $f(-0.5) = 1$。

主元 $a$ 得：$g(a) = t^2 - 2at + 1 = -2t \cdot a + (t^2 + 1)$ 为一次函数。

则 $g(-1), g(1) \ge \max(f(x)) = 1$。（技巧：整个线段高于 $x$ 等价于两端高于 $x$。）

则 $t \in (-\infty, -2] \cup \{ 0 \} \cup [2, +\infty)$。

7. 构造函数 $f(x)$，使其满足：

$\forall x \in \R, f(x) > 0$。
$f(x)$ 的最小正周期为 $4 \pi$。
$f(x)$ 是 $\R$ 上的偶函数。
$f(x)$ 在区间 $(-4 \pi, -2 \pi)$ 上为增函数。
$\max \limits_x (f(x)) - \min \limits_x (f(x)) \ge 4$。

正解：根据第一个条件，设 $f(x) = |A \sin(\omega x + \varphi)|$。

根据最后一个条件，可以令 $A = 4$。

根据第 2 个条件，可知 $\sin(\omega x + \varphi)$ 的周期为 $8 \pi$，则 $\omega = \dfrac{1}{4}$。

根据第 3 个条件，可知需要向左平移 $2 \pi$，故 $\varphi = \dfrac{\pi}{2}$。

这时，$f(x) = \left| 4 \sin \left( \dfrac{1}{4}x + \dfrac{\pi}{2} \right) \right|$。

发现它不满足第 4 个条件，它在区间 $(-4 \pi, -2 \pi)$ 上为减函数。

发动人类智慧，只需让 $f$ 关于 $y = 2$ 对称一下即可，故答案为 $f(x) = 4 - \left| 4 \sin \left( \dfrac{1}{4}x + \dfrac{\pi}{2} \right) \right|$。

8. 求方程 $\sin(x) = \lg(x + 1)$ 的实数解的个数。

正解 ^[2]：该方程定义在 $x > -1$ 上。对数函数 $\log_{10}(x + 1)$ 在 $x \in [-0.9, 9]$ 内取值于 $[-1, 1]$，因为当 $x = -0.9$ 时 $\log_{10}(x + 1) = -1$，当 $x = 9$ 时 $\log_{10}(x + 1) = 1$。在此区间外，$\sin(x)$ 在 $[-1, 1]$ 振荡，但 $\log_{10}(x + 1) < -1$ 当 $x < -0.9$ 且 $\log_{10}(x + 1) > 1$ 当 $x > 9$，因此无解。

在 $[-0.9, 9]$ 内，定义函数 $f(x) = \sin(x) - \log_{10}(x + 1)$，它是连续的，其零点对应方程的解。分析函数行为：

在 $x = -0.9$ 时，$f(-0.9) \approx 0.217 > 0$。

$f(x)$ 在约 $x \approx -0.82$ 处从正变负（根1）。

在 $x = 0$ 时，$f(0) = 0$（根2），且 $f(x)$ 在此处从负变正。

对于 $x > 0$，$f(x) > 0$ 直到在 $(\pi/2, \pi) \approx (1.57, 3.14)$ 内约 $x \approx 2.6$ 处从正变负（根3）。

在 $[\pi, 2\pi] \approx [3.14, 6.28]$ 内 $f(x) < 0$ 且无根。

$f(x)$ 在 $(2\pi, 5\pi/2) \approx (6.28, 7.85)$ 内约 $x \approx 7.4$ 处从负变正（根4）。

$f(x)$ 在 $(5\pi/2, 9] \approx (7.85, 9]$ 内约 $x \approx 8.2$ 处从正变负（根5）。

这些根分别位于：

$x \approx -0.82$，在 $(-0.9, -0.8)$ 内，

$x = 0$，

$x \approx 2.6$，在 $(1.57, 3.14)$ 内，

$x \approx 7.4$，在 $(7, 7.5)$ 内，

$x \approx 8.2$，在 $(8, 8.5)$ 内。

在此区间内无其他根，因为 $f(x)$ 在其他地方不改变符号。因此，共有 5 个实数解。

9. 设常数 $a \in (0, 1)$，函数 $f(x) = \dfrac{a(\cos(x) + a)}{2a \cos(x) + a^2 + 1}$，求 $\max(f(x)), \min(f(x))$。

10.1. $f(x) = 2 \sqrt{3} \sin \left( 3 \omega x + \dfrac{\pi}{3} \right), \omega > 0$ 在 $\left( -\dfrac{\pi}{3}, \dfrac{\pi}{2} \right)$ 上为增函数，求 $\max(\omega)$。

正解：容易发现，周期 $T = \dfrac{2 \pi}{3 \omega}$，一个最大值为 $\left( \dfrac{\pi}{18 \omega}, 2 \sqrt{3} \right)$。

则单调增区间为 $\left( \dfrac{-5 \pi}{18 \omega}, \dfrac{\pi}{18 \omega} \right) \supe \left( -\dfrac{\pi}{3}, \dfrac{\pi}{2} \right)$。

则有：

\[\begin{cases} -5 \pi / 18 \omega \le -\dfrac{\pi}{3} \\ \pi / 18 \omega \ge \dfrac{\pi}{2} \end{cases} \]
解得 $\omega \in (0, 1/9]$，则 $\max(\omega) = 1/9$。

10.2. $f(x) = 2 \sqrt{3} \sin \left( 3 \omega x + \dfrac{\pi}{3} \right), \omega > 0$ 在 $\left( \dfrac{\pi}{3}, \dfrac{\pi}{2} \right)$ 上为增函数，求 $\max(\omega)$。

正解：容易发现，周期 $T = \dfrac{2 \pi}{3 \omega}$，一个最大值为 $\left( \dfrac{\pi}{18 \omega}, 2 \sqrt{3} \right)$。

则单调增区间为 $\left( \dfrac{12k - 5}{18 \omega} \pi, \dfrac{12k + 1}{18 \omega} \pi \right) \supe \left( \dfrac{1}{3} \pi, \dfrac{1}{2} \pi \right)$。

则有：

\[\begin{cases} 12k - 5 \le 6 \omega \\ 12k + 1 \ge 9 \omega \end{cases} \]
解得 $\omega \in \left[ \dfrac{12k - 5}{6}, \dfrac{12k + 1}{9} \right]$，则 $\dfrac{12k - 5}{6} \le \dfrac{12k + 1}{9} \iff k \le \dfrac{17}{12}$。

则 $k = 1, \omega \in \left[ \dfrac{7}{6}, \dfrac{13}{9} \right]$，则 $\max(\omega) = \dfrac{13}{9}$。

11. 已知函数 $f : \Z \to \R$ 满足：

\[f(n) = \begin{cases} n - 10, &n > 100 \\ f(f(n + 11)), &n \le 100 \end{cases} \]

证明：$\forall n \le 100, f(n) = 91$。

证明：观察到，$90 + 11 = 101 > 100$，则我们先证明 $n \ge 90$ 的情形。

容易发现，此时 $f(n) = f(f(n + 11)) = f(n + 1)$，则 $f(100) = f(101) = 91$，则 $f(90) = f(91) = f(92) = \cdots = f(100) = 91$。

接下来对 $n$ 归纳，设 $n \ge n_0$ 时命题成立，我们证明 $n = n_0 - 1$ 时命题也成立。

此时 $f(n) = f(f(n + 11)) = f(f(n_0 + 10))$。因为 $n_0 + 10 \ge n_0$，所以 $f(n_0 + 10) = 91$，所以 $f(n) = f(f(n_0 + 10)) = f(91) = 91$。

证毕。

数论篇

1. 求证：对于给定非负整数 $n$ 与大于 $1$ 的正整数 $p$，存在非负整数 $k$ 和非负整数 $a_1, a_2, \cdots, a_k$（$\forall i, 0 \le a_i \le i$），使得 $n = \sum \limits_{i = 1}^k a_i \cdot i!$。

证明：在 $n = 0$ 时命题显然成立。设命题对于 $n \le n_0$ 都成立，下证明其对于 $n = n_0 + 1$ 成立。

若 $\exist t \in \N, n = t!$，那么 $n = \sum_{i = 1}^t [i = t] \cdot i!$。

否则，存在 $t$ 使得 $t! < n < (t + 1)!$，设 $n = a_t \cdot t! + r$ 满足 $r < t!$。则 $r < t! < n$，故原命题对 $r$ 成立。

设 $r = \sum \limits_{i = 1}^{t - 1} a_i \cdot i!$，则 $n = a_t \cdot t! + r = a_t \cdot t! + \sum \limits_{i = 1}^{t - 1} a_i \cdot i! = \sum \limits_{i = 1}^t a_i \cdot i!$。

故原命题对 $n \in \N$ 成立。

2. 证明方程 $x^2 + y^2 + z^2 = 15$ 没有有理根。

证明：设一个根为 $x = a_1 / b_1, y = a_2 / b_2, z = a_3 / b_3$ 满足 $\gcd(a_1, b_1) = \gcd(a_2, b_2) = \gcd(a_3, b_3) = 1$。则 $\left(\dfrac{a_1}{b_1} \right)^2 + \left(\dfrac{a_2}{b_2} \right)^2 + \left(\dfrac{a_3}{b_3} \right)^2 = 15$，即

\[\begin{aligned} (a_1 b_2 b_3)^2 + (b_1 a_2 b_3)^2 + (b_1 b_2 a_3)^2 = 15(b_1 b_2 b_3)^2 \tag{1} \end{aligned} \]
则

\[\begin{aligned} (a_1 b_2 b_3)^2 + (b_1 a_2 b_3)^2 + (b_1 b_2 a_3)^2 + (b_1 b_2 b_3)^2 = 16(b_1 b_2 b_3)^2 \tag{2} \end{aligned} \]
设 $A = a_1 b_2 b_3, B = b_1 a_2 b_3, C = b_1 b_2 a_3, D = b_1 b_2 b_3$，则 $A^2 + B^2 + C^2 + D^2 = 16D^2$。考虑 $A, B, C, D$ 的奇偶性：

$A, B, C, D$ 全为偶数：$b_1, b_2, b_3$ 中至少有一个偶数。

$A, B, C, D$ 全为奇数：此时 $A^2 \equiv B^2 \equiv C^2 \equiv D^2 \equiv 1 \pmod 8$，则 $A^2 + B^2 + C^2 + D^2 \equiv 4 \not \equiv 0 \equiv 16D^2 \pmod 8$，矛盾！

否则：$4$ 不整除 $A^2 + B^2 + C^2 + D^2$，矛盾！

故 $b_1, b_2, b_3$ 中至少有一个偶数，设其为 $b_1$。我们对偶数数量进行讨论：

有 1 个偶数：此时 $(2)$ 式中等号左边的后三项均为偶数，为使前一项 $(a_1 b_2 b_3)^2$ 也为偶数，$a_1$ 必为偶数。此时 $\gcd(a_1, b_1) = 2 \neq 1$，故原命题得证。

有 $\ge 2$ 个偶数：设 $b_1 = 2^m r_1, b_2 = 2^n r_2, b_3 = 2^p r_3$ 满足 $m \ge n \ge p \ge 0; m, n \ge 1; r_1 \equiv r_2 \equiv r_3 \equiv 1 \pmod 2$。则 $(1)$ 式变为

\[(a_1 2^n 2^p r_2 r_3)^2 + (a_2 2^m 2^p r_1 r_3)^2 + (a_3 2^m 2^n r_1 r_2)^2 = 15(2^m 2^n 2^p r_1 r_2 r_3)^2 \]
等号两边同除以 $(2^n 2^p)^2$，得

\[(a_1 r_2 r_3)^2 + (a_2 2^{m - n} r_1 r_3)^2 + (a_3 2^{m - p} r_1 r_2)^2 = 15(2^m r_1 r_2 r_3)^2 \]
因为等号右边为偶数，所以等号左边的每一项均为偶数，则 $2 \mid (a_1 r_2 r_3)^2 \implies 2 \mid a_1$。则 $\gcd(a_1, b_1) = 2 \not = 1$，故原命题得证。

3. 已知 $p \in \mathbb{P}_{> 3}$，求证：$\sum \limits_{i = 1}^{p - 1} (i^2)^{-1} \equiv 0 \pmod p$。

证明：注意到：

\[\begin{aligned} \sum \limits_{i = 1}^{p - 1} (i^2)^{-1} &\equiv \sum \limits_{i = 1}^{p - 1} (i^{-1})(i^{-1}) \\ &\equiv \sum \limits_{i = 1}^{p - 1} (i^{-1})^2 \end{aligned} \pmod p \]
而 $1, 2, \cdots, p - 1$ 为模 $p$ 的缩系，则 $1^{-1}, 2^{-1} \cdots, (p - 1)^{-1}$ 也为模 $p$ 的缩系。

故：

\[\begin{aligned} \sum \limits_{i = 1}^{p - 1} (i^2)^{-1} &\equiv \sum \limits_{i = 1}^{p - 1} (i^{-1})^2 \\ &\equiv \sum \limits_{i = 1}^{p - 1} i^2 \\ &\equiv \dfrac{p(p - 1)(2p - 1)}{6} \\ &\equiv 0 \end{aligned} \pmod p \]
证毕。

4. 求证：不存在连续 $18$ 个正整数，满足它们各恰有 $2$ 个质因子。

证明：因为有连续 $18$ 个正整数，故必有 $\dfrac{18}{6} = 3$ 个 $6$ 的倍数。设它们为 $6n, 6(n + 1), 6(n + 2)$。

因为这些正整数各恰有 $2$ 个质因子，而 $6$ 已经有 $2$ 个质因子（$2$ 与 $3$），故 $n, n + 1, n + 2$ 都只能有 $2, 3$ 这两个质因子。

满足条件的只有 $n = 1$ 与 $n = 2$ 两种情况，检验可发现它们都不满足条件，故不存在满足给定条件的构造。证毕。

5. 设 $a, b, c, d, e$ 为互不相等的正整数，且满足 $a^4 + b^4 = c^4 + d^4 = e^5$。求证：$ac + bd$ 为合数。

证明：设 $ac + bd = p \in \mathbb{P}, a = \max(a, b, c, d)$，则 $b = \min(a, b, c, d)$，且：

\[\begin{aligned} ac \equiv -bd \pmod p &\leadsto a^4 c^4 \equiv b^4 d^4 \pmod p \\ &\leadsto a^4 c^4 + b^4 c^4 \equiv b^4 d^4 + b^4 c^4 \equiv a^4 b^4 + b^8 \pmod p \\ &\leadsto (a^4 + b^4)(c^4 - b^4) \equiv 0 \pmod p \\ &\leadsto p \mid (a^4 + b^4)(c^2 + b^2)(c + b)(c - b) \end{aligned} \]
故 $p$ 整除 $a^4 + b^4, c^2 + b^2, c + b, c - b$ 中的一个。

因为 $a > c, d > b$，所以 $p = ac + bd > c^2 + b^2 > c \pm b$，所以 $p \mid a^4 + b^4$，所以 $p \mid e^5 \implies p \mid e$。

考虑 $a$ 与 $e$ 的大小关系。

我们发现，$e^5 = a^4 + b^4 < 2a^4 \implies e < 2^{1/5} a^{4/5}$。

因为 $2^{1/5} a^{4/5} < a \iff 2 < a$，又因为 $a, b, c, d$ 为互不相等的正整数，所以 $a \ge 4$，所以 $e < 2^{1/5} a^{4/5} < a$。

而 $p > a > e$，与 $p \mid e$ 矛盾！故 $p \notin \mathbb{P}$。

6. 设 $n \in \N^+$。证明：存在整数 $m$ 满足 $2^n \mid 2018m^2 + 20182017m + 2017$。

证明（归纳法）：考虑加强命题。

我们证明：对于 $a, b, c$ 满足 $a, c$ 中至少有一个偶数，$b$ 为奇数，存在整数 $m$ 满足 $2^n \mid am^2 + bm + c$。

在 $n = 1$ 时：

$2 \mid c$：取 $m = 0$ 即可。

$2 \nmid c$：取 $m = c$ 即可。

故 $n = 1$ 时命题成立。

假设 $n = n_0$ 时命题成立，下证 $n = n_0 + 1$ 时命题成立。

对 $c$ 的奇偶性分类讨论：

$2 \mid c$：注意到，$\exist t, 2at^2 + bt + \dfrac{c}{2} \equiv 0 \pmod{2^{n_0}}$，

则 $4at^2 + 2bt + c \equiv 0 \pmod{2^{n_0 + 1}}$，

则 $a(2t)^2 + b(2t) + c \equiv 0 \pmod{2^{n_0 + 1}}$，

则只需取 $m = 2t$ 即可。

$2 \nmid c$：注意到，$\exist t, 2at^2 + (2a + b)t + \dfrac{a + b + c}{2} \equiv 0 \pmod{2^{n_0}}$，

则 $4at^2 + 4at + bt + a + b + c \equiv 0 \pmod{2^{n_0 + 1}}$，

则 $a(2t + 1)^2 + b(2t + 1) + c \equiv 0 \pmod{2^{n_0 + 1}}$，

则只需取 $m = 2t + 1$ 即可。（技巧：由结论反推过程。）

故此时命题成立，证毕。

评注：在条件缺少时，一般采用归纳法。

7. 设 $n \in \N^+$，证明：数列 $2, 2^2, 2^{2^2}, 2^{2^{2^2}}, \cdots$ 在模 $n$ 意义下最终为常数。

证明（归纳法）：注意到，该数列的通项公式为 $a_1 = 2, a_n = 2^{a_{n - 1}}$。

在 $n \le 2$ 时，命题正确。设 $n < k$ 时命题正确，下证 $n = k$ 时命题正确。

设 $k = 2^{\alpha} \beta$ 满足 $2 \perp \beta$，则在 $n = \varphi(\beta) < k$ 时，$\exist i, a_{i + 1} \equiv 2^{a_i} \equiv c \pmod{\varphi(\beta)}$。

又因为 $2$ 模 $\beta$ 的阶 $T \mid \varphi(\beta)$，所以 $2^{2^{a_i}} \equiv 2^c \equiv 2^{a_{i + 1}} \pmod \beta$。

······

8. 求方程 $x^3 + y^3 + z^3 = 2018^{2018}$ 的所有正整数解。

正解：注意到，立方数模 $9$ 的余数只能是 $0, 1, 8$。考虑计算 $2018^{2018} \bmod 9$。

注意到，$2018^{\varphi(9)} \equiv 2018^6 \equiv 1 \pmod 9$，则 $2018^{2018} \equiv (2018^6)^{336} \cdot 2018^2 \equiv 4 \pmod 9$。

因为三个立方数之和模 $9$ 不可能为 $4$，故无解。

9. 给定 $u, v \in \N^+$，定义数列 $a$：

\[\begin{cases} a_1 = u + v \\ a_{2n} = a_n + u \\ a_{2n + 1} = a_n + v \end{cases} \]

定义数列 $S_n = \sum \limits_{i = 1}^n a_i$，证明：$S$ 中有无穷多个完全平方数。

证明：注意到：

\[\begin{aligned} S_{2^{n + 1} - 1} &= a_1 + (a_2 + a_3) + (a_4 + a_5) + \cdots + (a_{2^{n + 1} - 2} + a_{2^{n + 1} - 1}) \\ &= a_1 + (2a_1 + u + v) + (2a_2 + u + v) + \cdots + (2a_{2^n - 1} + u + v) \\ &= 2^n (u + v) + 2S_{2^n - 1} \end{aligned} \]
则 $S_{2^n - 1} = 2^{n - 1} \cdot n \cdot (u + v)$。

证明（生成函数）：设 $T_n = S_{2^{n + 1} - 1}, C = u + v, T(x) = \sum \limits_{n \ge 0} T_n x^n$。

则 $T_{n + 1} = 2^{n + 1} C + 2T_n$，则有：

\[\begin{aligned} \dfrac{T(x) - C}{x} &= \sum \limits_{n \ge 0} T_{n + 1} x^n \\ &= \sum \limits_{n \ge 0} (2^{n + 1} C + 2T_n) \cdot x^n \\ &= 2C \sum \limits_{n \ge 0} 2^n x^n + 2 \sum \limits_{n \ge 0} T_n x^n \\ &= \dfrac{2C}{1 - 2x} + 2T(x) \end{aligned} \]
则：

\[\begin{aligned} \dfrac{T(x) - C}{x} = \dfrac{2C}{1 - 2x} + 2T(x) &\implies T(x) - C = \dfrac{2Cx}{1 - 2x} + 2x \cdot T(x) \\ &\implies (1 - 2x) \cdot T(x) = C + \dfrac{2Cx}{1 - 2x} \\ &\implies T(x) = \dfrac{C}{1 - 2x} + 2C \cdot \dfrac{x}{(1 - 2x)^2} = \dfrac{C}{(1 - 2x)^2} = \sum \limits_{n \ge 0} 2^n C (n + 1) \cdot x^n \\ &\implies T_n = 2^n C (n + 1) \end{aligned} \]
则 $S_{2^{n + 1} - 1} = T_n = 2^n (u + v)(n + 1) \implies S_{2^n - 1} = 2^{n - 1} n (u + v)$，证毕。

设 $u + v = 2^k \cdot m$ 满足 $k \ge 0, 2 \nmid m$，则 $S_{2^n - 1} = 2^{n + k - 1} nm$。

若 $2 \mid k$：令 $n = a^2 m \quad (\forall 2 \nmid a)$。

否则：令 $n = 4a^2 m \quad (\forall a \in \N_+)$。

10. 证明：$a - b \mid a^n - b^n \quad (a \ge b, n \ge 0; a, b, n \in \mathbb N)$。

证明（归纳法）：已知 $(a - b) \mid (a^0 - b^0)$，假设 $(a - b) \mid (a^n - b^n)$ 成立，我们证明 $(a - b) \mid (a^{n + 1} - b^{n + 1})$。

我们进行变形：

\[\begin{aligned} a^{n + 1} - b^{n + 1} &= a \cdot a^n - b \cdot b^n \\ &= (a - b) a^n + b \cdot a^n - b \cdot b^n \\ &= (a - b) a^n + b (a^n - b^n) \end{aligned} \]
此时，因为 $(a - b) \mid (a - b) a^n$，且 $(a - b) \mid b (a^n - b^n)$，所以 $(a - b) \mid (a^{n + 1} - b^{n + 1})$。

故原命题成立。

组合数学篇

1. 有 $6$ 名女同学和 $15$ 名男同学围成一个圈跳舞，要求每两名女同学之间至少有两名男同学，求围圈的方案数。

思路：我们发现，如果相邻的同学挨在一起就会很好做，但是每两名女同学之间至少有两名男同学。所以我们可以把两名男同学拆散，各给一名女同学，这样他们的捆绑体就可以挨在一起算。

正解：考虑把一名女同学和两名男同学捆绑在一起，这样就有 $6$ 个捆绑体和 $3$ 个多余的男同学，共 $9$ 个。对他们做圆排列，有 $8!$ 种方案。

再考虑每一个捆绑体内部。我们发现，被捆绑的男同学可以随意交换位置以获得新的方案，故共有 $\dbinom{15}{12} \cdot 12!$ 种方案。

则根据乘法原理，共有 $\dbinom{15}{12} \cdot 12! \cdot 8! = 8787571752960000$ 种方案。

2. 已知集合 $A$ 满足：

$A \sube \{ 1, 2, \cdots, 100 \}$。
若 $x \in A$，则 $2x \notin A$。

求 $\max(|A|)$。

正解：建无向图 $G$，把 $x$ 和 $2x$ 连边，则答案为 $G$ 中最大独立集的大小。

注意到 $G$ 是由一条条链组成的，所以只需对每条链求最大独立集大小，然后再加起来。

长度为 $l$ 的链的最大独立集大小为 $\lceil l / 2 \rceil$。

下附代码，输出为 $67$。
#include <iostream>
#include <vector>

using namespace std;

constexpr int N = 100;

vector<vector<int>> G(N + 1);
vector<bool> vis(N + 1);

int size(int u)
{
    int res = 1;
    vis[u] = true;

    for (int v : G[u]) {
        if (!vis[v])
            res += size(v);
    }

    return res;
}

int main()
{
    for (int i = 1; i <= N / 2; ++i) {
        G[i].emplace_back(i * 2);
        G[i * 2].emplace_back(i);
    }

    int ans = 0;

    for (int i = 1; i <= N; ++i) {
        if (!vis[i])
            ans += (size(i) + 1) / 2;
    }

    cout << ans << '\n';
    return 0;
}

3. 设 $S_n = \{ 1, 2, 3, \ldots, n \}$。若 $X \subseteq S_n$，若 $\sum \limits_{x \in X} x$ 为奇（偶）数，把 $X$ 称为 $S_n$ 的奇（偶）子集。

设 $S_{\rm odd}(n), S_{\rm even}(n)$ 分别为 $S_n$ 的全体奇、偶子集的集合。证明：在 $n \ge 3$ 时：

\[\sum_{S \in S_{\rm odd}(n)} \sum_{x \in S} x = \sum_{S \in S_{\rm even}(n)} \sum_{x \in S} x \]

证明：我们先算一下 $\rm LHS$ 和 $\rm RHS$。

很明显要分析每个元素的贡献。设 $i$ 在 $\rm LHS$ 贡献 $c_{\rm odd}(i)$，在 $\rm RHS$ 贡献 $c_{\rm even}(i)$。

我们只关心模 $2$ 意义下的值，则 $S_n$ 中有 $\lceil n / 2 \rceil$ 个 $1$，$\lfloor n / 2 \rfloor$ 个 $0$。

分类讨论 $i$ 的奇偶性：

$2 \mid i$：那么需要选奇数个 $1$，有 $2^{\lceil n / 2 \rceil - 1}$ 中方案。$0$ 中必须选 $i$，所以有 $2^{\lfloor n / 2 \rfloor - 1}$ 中选法。故 $c_{\rm odd}(i) = 2^{n - 2}$。

同理可得 $c_{\rm even}(i) = 2^{n - 2}$。

$2 \nmid i$：还是要选奇数个 $1$，但 $i$ 必选，所以剩下的 $1$ 要选偶数个，有 $2^{\lceil n / 2 \rceil - 2}$ 中方案。$0$ 随便选，所以有 $2^{\lfloor n / 2 \rfloor}$ 中选法。故 $c_{\rm odd}(i) = 2^{n - 2}$。

同理可得 $c_{\rm even}(i) = 2^{n - 2}$。

故 $c_{\rm odd}(i) = c_{\rm even}(i) = 2^{n - 2}$。

故 ${\rm LHS} = \sum \limits_{i = 1}^n i \cdot c_{\rm odd}(i) = 2^{n - 2} \sum \limits_{i = 1}^n i = 2^{n - 3} n (n + 1)$，${\rm RHS} = \sum \limits_{i = 1}^n i \cdot c_{\rm even}(i) = 2^{n - 2} \sum \limits_{i = 1}^n i = 2^{n - 3} n (n + 1) = {\rm LHS}$。

证毕。

评注：这里的 $n \ge 3$ 是有原因的。分析刚才的证明的逻辑，我们发现只有 $\lceil n / 2 \rceil - 2 \ge 0$ 且 $\lfloor n / 2 \rfloor - 1 \ge 0$ 时逻辑才成立。这个条件等价于 $n \ge 3$。

而且 $n = 2$ 时原命题确实是错的。

神秘题目

1. 定义集合 $A$ 是“好集”，当且仅当：

$0, 1 \in A$。
若 $x, y \in A$，则 $x \pm y \in A$。
若 $x \in A, x \neq 0$，则 $\dfrac{1}{x} \in A$。

求证：若 $x, y \in A$，则 $xy \in A$。

证明：注意到 $2xy = (x + y)^2 - x^2 - y^2$。

引理：若 $x \in A$，则 $x^2 \in A$。

证明：

\[\begin{aligned} x \in A, 1 \in A &\implies x - 1 \in A, \dfrac{1}{x} \in A \\ &\implies \dfrac{1}{x - 1} \in A \\ &\implies \dfrac{1}{x - 1} - \dfrac{1}{x} = \dfrac{1}{x^2 - x} \in A \\ &\implies x^2 - x \in A \\ &\implies x^2 \in A \end{aligned} \]

根据该引理，有 $(x + y)^2, x^2, y^2 \in A$，故 $2xy \in A$。

则 $\dfrac{1}{2xy} \in A \implies \dfrac{1}{2xy} + \dfrac{1}{2xy} = \dfrac{1}{xy} \in A \implies xy \in A$。

2. 对于一个正整数 $n$，若其满足以下条件，则称其为“金猴数”：

$n$ 可以被分解为若干个正整数相加。
这些正整数的倒数和为 $1$。

解决以下问题：

2.1. 证明：$11$ 和 $28$ 是两个“金猴数”。

正解：因为 $11 = 2 + 3 + 6$，且 $1/2 + 1/3 + 1/6 = 1$，所以 $11$ 是“金猴数”。因为 $28 = 8 + 8 + 4 + 4 + 4$，且 $1/8 + 1/8 + 1/4 + 1/4 + 1/4 = 1$，所以 $11$ 是“金猴数”。

2.2. 证明：若 $n$ 是“金猴数”，则 $2n + 2$ 与 $2n + 9$ 均为“金猴数”。

正解：设 $n = \sum \limits_j a_j$，则 $\sum \limits_j \dfrac{1}{a_j} = 1$，则 $\sum \limits_j \dfrac{1}{2a_j} = 1/2$，则 $1/2 + \sum \limits_j \dfrac{1}{2a_j} = 1$。又发现 $2n + 2 = 2 + \sum \limits_j 2a_j$，且 $1/2 + \sum \limits_j \dfrac{1}{2a_j} = 1$，所以 $2n + 2$ 是“金猴数”。

又发现 $1/3 + 1/6 + \sum \limits_j \dfrac{1}{2a_j} = 1$，则 $2n + 9 = 3 + 6 + \sum \limits_j 2a_j$，且 $1/3 + 1/6 + \sum \limits_j \dfrac{1}{2a_j} = 1$，所以 $2n + 9$ 是“金猴数”。

2.3. 证明：$2023$ 是“金猴数”。

正解：

因为 $28$ 是“金猴数”，

所以 $28 \times 2 + 2 = 58$ 是“金猴数”，

所以 $58 \times 2 + 2 = 118$ 是“金猴数”，

所以 $118 \times 2 + 9 = 245$ 是“金猴数”。

所以 $245 \times 2 + 9 = 499$ 是“金猴数”。

所以 $499 \times 2 + 9 = 1007$ 是“金猴数”。

所以 $1007 \times 2 + 9 = 2023$ 是“金猴数”。

该解法由小智提出。 ↩︎
该解法由 DeepSeek 提出。 ↩︎

posted @ 2025-07-31 10:00 David9006 阅读(82) 评论(0) 收藏举报

刷新页面返回顶部

Gapple

No one believes fairytales anymore / But our two hearts in sync / To wish upon a satellite

做题记录（MO）

代数篇

几何篇

函数篇

数论篇

组合数学篇

神秘题目

公告