好题集

• 代数篇
• 几何篇
• 函数篇
• 数论篇
• 组合数学篇
• 神秘题目

记号约定：

• \(\mathbb{P}\)：全体质数集合。
• \(a \perp b\)：直线 \(a\) 与 \(b\) 垂直；整数 \(a\) 和 \(b\) 互质。
• \(a \parallel b\)：直线 \(a\) 与 \(b\) 平行；（规定 \(\exist i \in \mathbb{N}, p \in \mathbb{P}, a = p^i\)）整数 \(p^i, b\) 满足 \(p^i \mid b, p^{i + 1} \nmid b\)。
• \(\nu_p(n)\)：质数 \(p\) 在整数 \(n\) 的质因数分解中的幂次。
• \([x^n] f(x)\)：多项式 \(f(x)\) 中 \(x^n\) 的系数。
• （Iverson 括号）\([\mathrm{P}]\)：命题 \(\mathrm{P}\) 为真时取 \(1\)，否则取 \(0\)。

更新记录：

• 2025.8.11。
• 2025.11.29：适配 MathJax 3。

代数篇

1. 已知非零实数 \(a,b,c,x,y,z\) 满足

\[x^2+y^2+z^2=a^2+b^2+c^2=ax+by+cz \]

求证：\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\)。

设 \(x^2+y^2+z^2=a^2+b^2+c^2=ax+by+cz=k\)。则：

\[\begin{aligned} k+k-2k &= x^2+y^2+z^2+a^2+b^2+c^2-2ax+2by+2cz \\ &= (a^2-2ax+x^2)+(b^2-2by+y^2)+(c^2-2cz+z^2) \\ &= (a-x)^2+(b-y)^2+(c-z)^2 \\ &= 0 \end{aligned} \]

这说明 \(a=x,b=y,c=z \implies \dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=1\)，证毕。

2. 若 \(\dfrac{x}{y+z}+\dfrac{y}{x+z}+\dfrac{z}{x+y}=1\)，求 \(\dfrac{x^2}{y+z}+\dfrac{y^2}{x+z}+\dfrac{z^2}{x+y}\) 的值。

正解：则：

\[\begin{aligned} \dfrac{x(x+y+z)}{y+z}+\dfrac{y(x+y+z)}{x+z}+\dfrac{z(x+y+z)> }{x+y} &= \sum_{\text{cyc}} \dfrac{x^2+x(y+z)}{y+z} \\ &= \sum_{\text{cyc}} \dfrac{x^2}{y+z}+(x+y+z) \\ &= x+y+z \end{aligned} \]

故原式为 \(0\)。

3. 已知关于 \(x\) 的方程 \(x^2 - 2|x| + 2 = m\) 恰有 3 个实数根，求 \(m\) 的值。

正解（换元法）：设 \(A = |x|\)，则 \(A^2 - 2A + 2 = m\)。我们发现：

• 当 \(A = 0\) 时，会产生 1 个实数根。
• 否则，会产生 2 个实数根。

则因为原方程有 3 个实数根，且 \(A\) 最多有 2 个不同的值，所以一定有 \(A > = 0\) 这一根。代入原方程得 \(m = 2\)。

4. 设实数 \(a, b, c\) 满足：

• \(a \le b \le c\)，
• \(ab + bc + ca = 0\)，
• \(abc = 1\)。

求最大的 \(k\)，满足 \(|a + b| \ge k|c|\)。

正解：由条件可知：\(ab = \dfrac{1}{c}\)，则 \(ab + bc + ca = ab + (a + b)c = \dfrac{1}{c} + (a + b)c = 0\)，则 \(a + b = -\dfrac{1}{c^2}\)。则

\[\begin{cases} a + b = -\dfrac{1}{c^2} \\ ab = \dfrac{1}{c} \end{cases} \]

这说明 \(x_1 = a, x_2 = b\) 为方程 \(x^2 + \dfrac{1}{c^2} x + \dfrac{1}{c} = 0\) 的两根。（技巧：看到 \(a + b, ab\) 就要想到韦达定理。）

为保证其有两根，考虑其判别式：

\[\begin{aligned} \Delta &= \dfrac{1}{c^4} - \dfrac{4}{c} \\ &= \dfrac{1 - 4c^3}{c^4} \\ & \ge 0 \end{aligned} \]

则 \(1 - 4c^3 \ge 0 \implies c^3 \le \dfrac{1}{4}\)。

再考虑 \(|a + b| \ge k|c|\)，则 \(k \le \left| \dfrac{a + b}{c} \right| = \left| \dfrac{1}{c^3} \right|\)。

考虑 \(c\) 的符号：因为 \(ab + bc + ca = 0\)，所以 \(\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} = 0\)。则有两负一正或两正一负，故 \(\dfrac{1}{c} > 0 \implies c > 0\)。

则 \(0 \le c^3 \le \dfrac{1}{4} \implies \dfrac{1}{c^3} \ge 4\)，则 \(k \le \dfrac{1}{4} \implies \max(k) = \dfrac{1}{4}\)。

5. 设 \(A = 1 - \dfrac{1}{2} + \dfrac{1}{3} - \dfrac{1}{4} + \cdots + \dfrac{1}{99} - \dfrac{1}{100}, B = \dfrac{1}{100 \times 102} + \dfrac{1}{100 \times 104} + \cdots + \dfrac{1}{100 \times 200}\)，求 \(A/B\) 的值。

正解：设 \(S_n = \sum_{j = 1}^n 1/j\)，我们尝试用 \(S_n\) 表示 \(A, B\)。

容易发现

\[\begin{aligned} A &= \left( 1 + \dfrac{1}{2} + \dfrac{1}{3} + \cdots + \dfrac{1}{100} \right) - 2 \times \left( \dfrac{1}{2} + \dfrac{1}{4} + \cdots + \dfrac{1}{100} \right) \\ &= \left( 1 + \dfrac{1}{2} + \dfrac{1}{3} + \cdots + \dfrac{1}{100} \right) - \left( 1 + \dfrac{1}{2} + \dfrac{1}{3} + \cdots + \dfrac{1}{50} \right) \\ &= S_{100} - S_{50} \end{aligned} \]

同时

\[\begin{aligned} B &= \dfrac{1}{4} \times \left( \dfrac{1}{50 \times 51} + \dfrac{1}{50 \times 52} + \cdots + \dfrac{1}{50 \times 100} \right) \\ &= \dfrac{1}{4} \times \left( \dfrac{1}{50} \times \dfrac{1}{51} + \dfrac{1}{50} \times \dfrac{1}{52} + \cdots + \dfrac{1}{50} \times \dfrac{1}{100} \right) \\ &= \dfrac{1}{40} \times \dfrac{1}{50} \times \left( \dfrac{1}{51} + \dfrac{1}{52} + \cdots + \dfrac{1}{100} \right) \\ &= \dfrac{1}{200} \cdot (S_{100} - S_{50}) \\ &= \dfrac{1}{200} A \end{aligned} \]

故 \(A/B = 200\)。

6. 已知 \(a - \dfrac{1}{a} = 1\)，求 \(a^{12} + 48 a^{-4}\) 的值。

正解：原式为 \(a^4 (a^8 + 48 a^{-8})\)。（技巧：对称的次数更好处理。）

注意到 \(a^4 + a^{-4} = 7 \implies a^8 + a^{-8} = (a^4 + a^{-4})^2 - 2 = 47\)，与 \(48\) 只差 \(1\)，故原式为

\[\begin{aligned} a^4 (a^8 + 48 a^{-8}) &= a^4 (a^8 + (47 + 1) a^{-8}) \\ &= a^4 (a^8 + a^{-8} + (a^8 + a^{-8})a^{-8}) \\ &= a^4 (47 + 47 a^{-8}) \\ &= 47a^4 + 47a^{-4} \\ &= 47 \cdot 7 \\ &= 329 \end{aligned} \]

7. 已知 \(x, y, z \in \mathbb{R}^+\)，且 \(x + y + z = 1\)，求证：

\[\dfrac{1}{1 - x} + \dfrac{1}{1 - y} + \dfrac{1}{1 - z} \ge \dfrac{2}{1 - x} + \dfrac{2}{1 - y} + \dfrac{2}{1 - z} \]

证明：由权方和不等式得：

\[\dfrac{1}{1 - x} + \dfrac{1}{1 - y} \ge \dfrac{4}{2 - x - y} = \dfrac{4}{1 + z} \]

同理有：

\[\dfrac{1}{1 - y} + \dfrac{1}{1 - z} \ge \dfrac{4}{1 + x} \\ \dfrac{1}{1 - z} + \dfrac{1}{1 - x} \ge \dfrac{4}{1 + y} \]

三式相加得：

\[2 \left( \dfrac{1}{1 - x} + \dfrac{1}{1 - y} + \dfrac{1}{1 - z} \right) \ge 2 \left( \dfrac{2}{1 - x} + \dfrac{2}{1 - y} + \dfrac{2}{1 - z} \right) \]

两边除以 \(2\) 即可。

几何篇

1. 已知 \(x^3 + y^3 = 16\)，求 \(xy\) 的最大值。

正解（面积法）：设 \(u = a^{1.5}, v = b^{1.5}\)。则 \(u^2 + v^2 = 16\)。

考虑其图象（半径为 2、以原点为圆心的圆）。如图，\(u = AB, v = AC, uv = S_{ABDC}\)。

容易发现，在 \(AD \perp BC\) 时，\(S_{ABDC}\) 最大，为 8。此时 \((ab)^{1.5} = uv = 8\)。

则 \((ab)^3 = 64 \implies ab = 4\)。

故最大值为 4。

2. 在 \(\triangle ABC\) 中，\(BC = 6\)，\(BC\) 上的高 \(AD = 3\)，作 \(\triangle ABC\) 的一个内接正方形，使得它的两个顶点都在 \(AB\) 和 \(AC\) 上，求该正方形的边长。

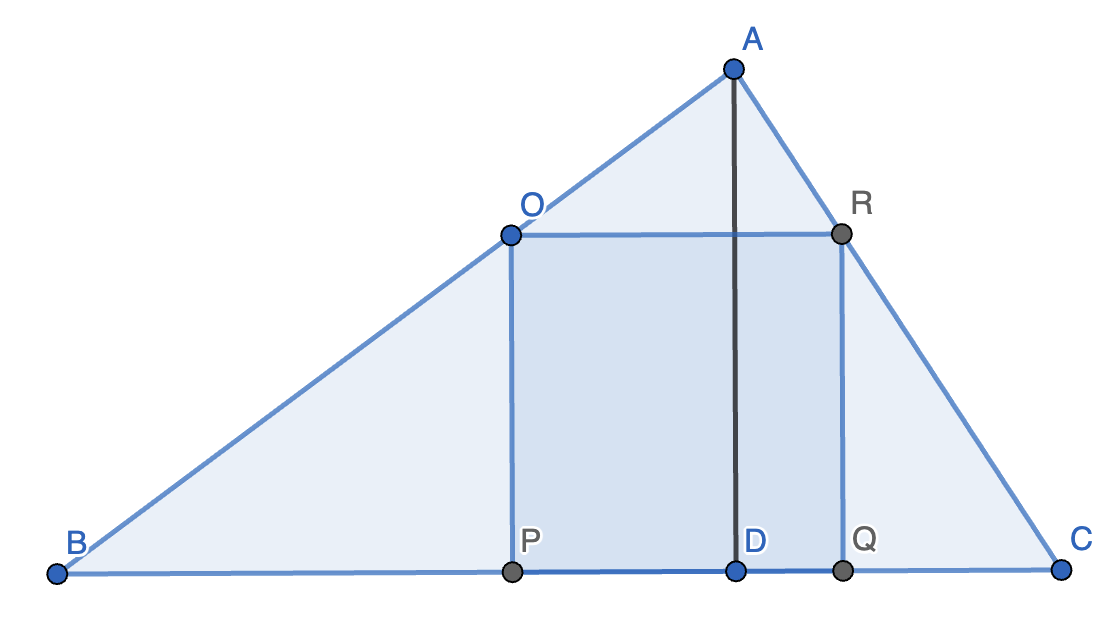
正解：设正方形的边长为 \(x\)，\(OR\) 交 \(AD\) 于点 \(P\)，则 \(AP = 3 - x\)。

因为 \(\triangle AOR \sim \triangle ABC\)，所以 \(\dfrac{AS}{OR} = \dfrac{AD}{BC}\)，即 \(\dfrac{3 - x}{x} = \dfrac{3}{6}\)，解得 \(x = 2\)。

3. 如图，在 \(\triangle ABC\) 中，\(\angle BAC = 100 \degree\)，\(\angle ABC = 50 \degree\)，延长 \(AC\) 至 \(D\)，使得 \(CD = AB\)，连接 \(BD\)，求 \(\angle D\) 的度数。

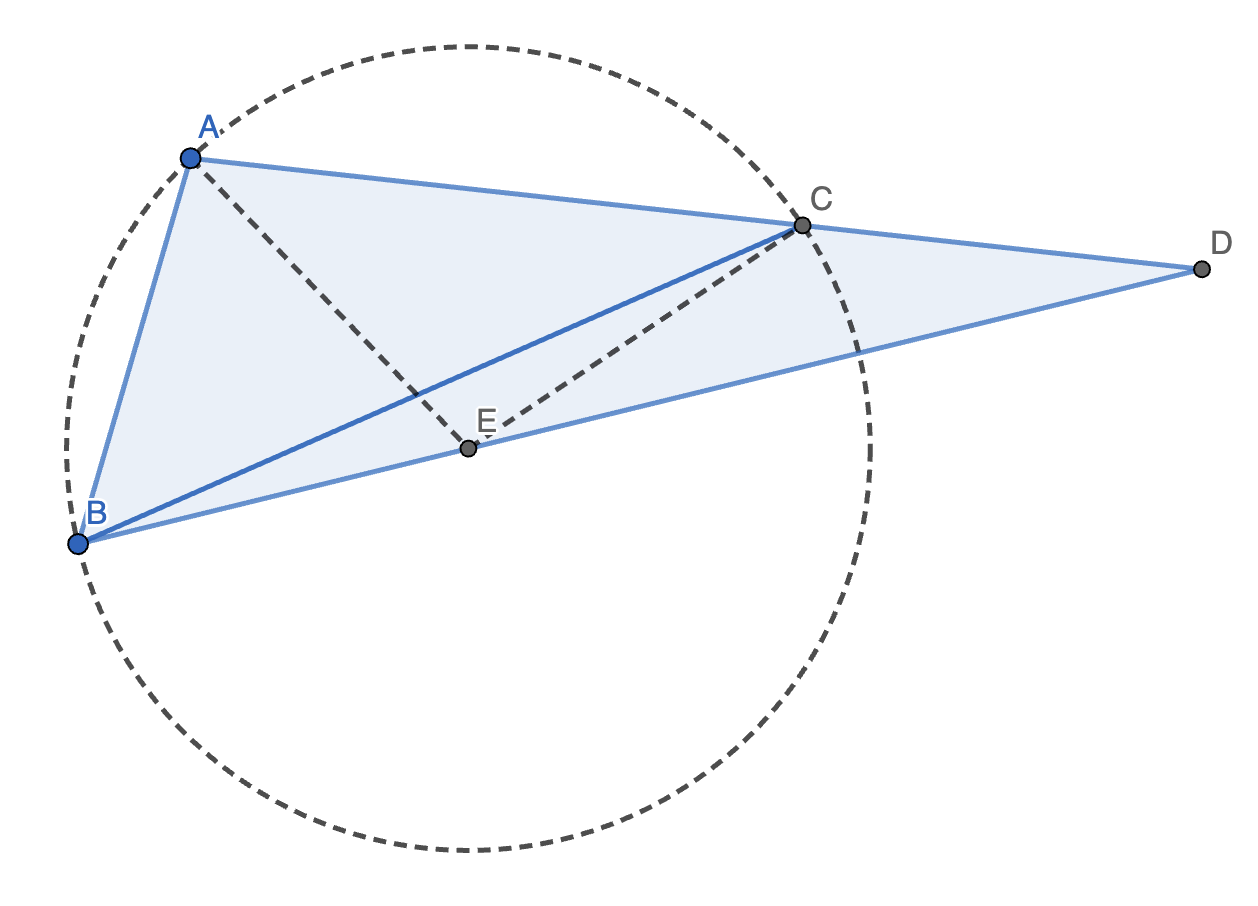
正解：作 \(\triangle ABC\) 的外接圆 \(\odot E\)，连接 \(AE, CE\)。

可以发现，\(\angle AEB = 2 \angle ACB = 60 \degree\)，所以 \(AB = AE = BE = CD = CE \implies \angle BAE = 60 \degree \implies \angle CAE = \angle ACE = 40 \degree \implies \angle DCE = 140 \degree \implies \angle D = 20 \degree\)。

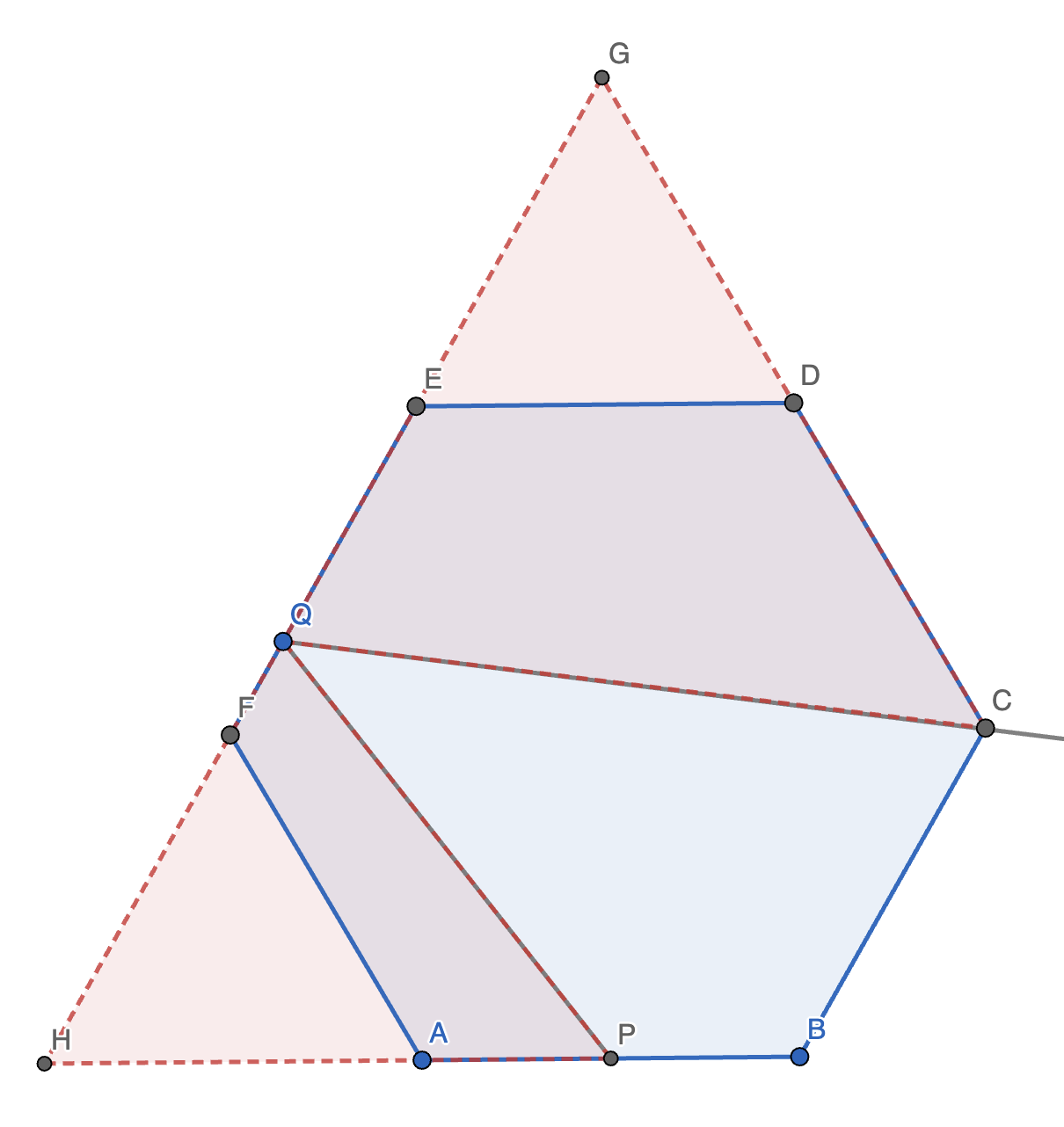
4. 在正六边形 \(ABCDEF\) 中，\(P\) 为 \(AB\) 的中点。光线 \(PQ\) 经过边 \(EF\) 反射后，恰好经过点 \(C\)。求 \(EQ\) 的值。

解法 1：

如图，作 \(ABCDEF\) 关于 \(EF\) 对称的图形 \(\omega\)，延长 \(PQ\) 交 \(\omega\) 于 \(H\)。

作 \(KQ \perp BC\) 于 \(K\)，\(JP \perp BC\) 于 \(J\)。（技巧：遇到相等的角，要让它们在一个三角形里，以便于分析。）

容易发现，\(\angle JBP = 60 \degree\)，且 \(\triangle IJP \sim \triangle IKQ\)。

故 \(JP = \dfrac{1}{2} \sqrt{3}, KQ = 2 \sqrt{3}\)，故相似比为 \(1 : 4\)。

又知 \(BJ = \dfrac{1}{2}\)，故可列方程组：

\[\begin{cases} IJ + \dfrac{1}{2} + BK = 2 - BK \\ 3IJ = \dfrac{1}{2} + BK \end{cases} \]

解得：\(IJ = \dfrac{5}{14}, BK = \dfrac{4}{7}\)，故 \(CK = 2 - BK = \dfrac{10}{7}\)。

解法 2：

延长 \(PA\) 交 \(FQ\) 于 \(H\)，延长 \(CD\) 交 \(EQ\) 于 \(G\)。

可以发现，\(\angle HQP = \angle CQD, \angle H = \angle G = 60 \degree, CG = 4, HP = 3, \triangle HQP \sim \triangle GQC\)。

故 \((2 + EQ) : (4 - EQ) = CG : HP = 4 : 3 \implies EQ = \dfrac{10}{7}\)。

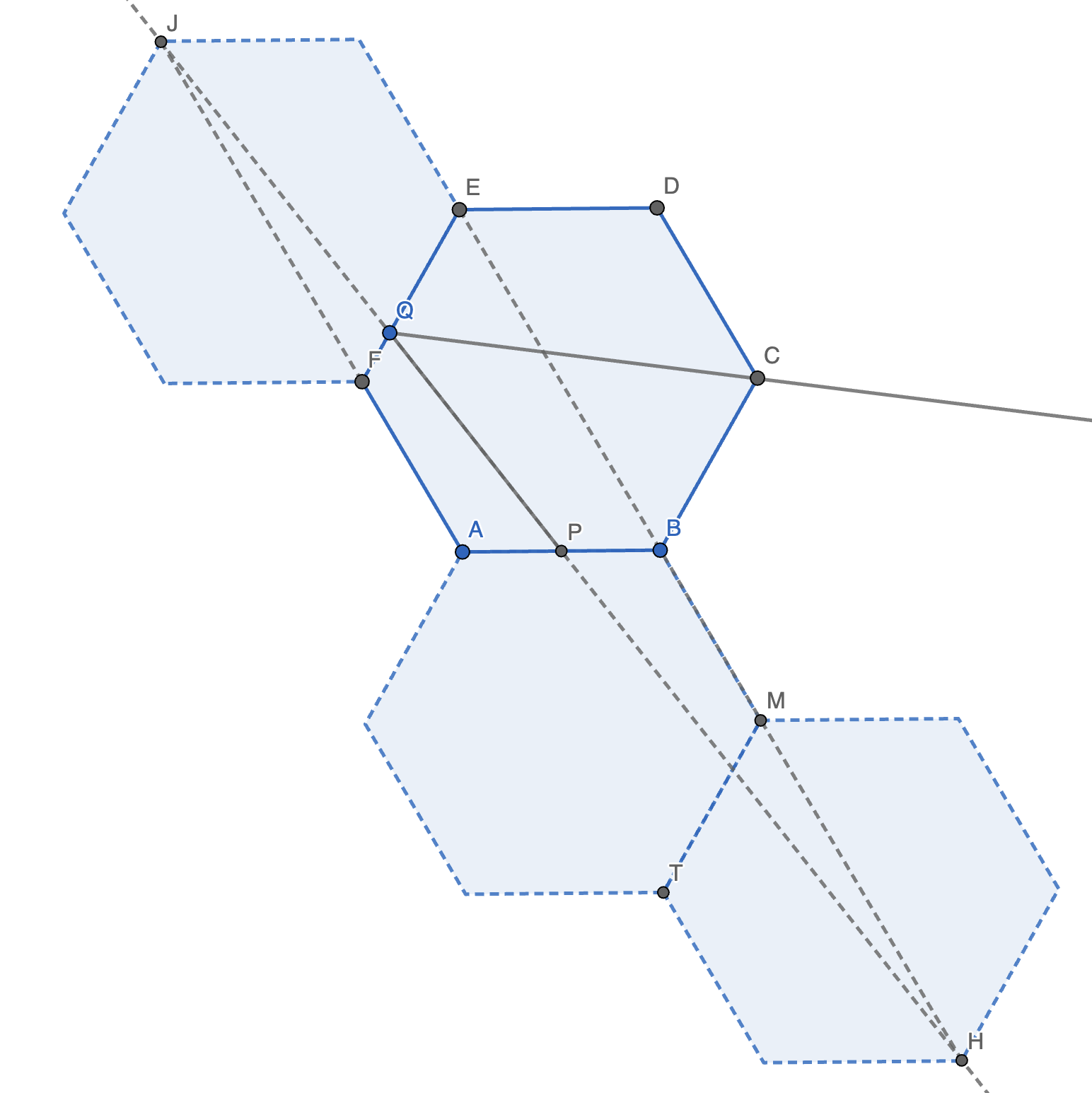
解法 3：

如图，将六边形 \(ABCDEF\) 关于 \(EF\) 对称得六边形 \(\omega_1\)，关于 \(AB\) 对称得 \(\omega_2\)。再将 \(\omega_2\) 关于 \(MT\) 对称得 \(\omega_3\)。连接并延长 \(EB\) 交 \(\omega_3\) 于 \(H\)。延长 \(AF\) 交 \(\omega_1\) 于 \(J\)，连接 \(JQ\)。

注意到，\(\angle FQJ = \angle EQH, \angle QFJ = \angle HEQ = 60 \degree\)，故 \(\triangle FJQ \sim \triangle EHQ\)。

故 \(EQ : (2 - EQ) = EH : FJ = 10 : 4 = 5 : 2 \implies EQ = \dfrac{10}{7}\)。

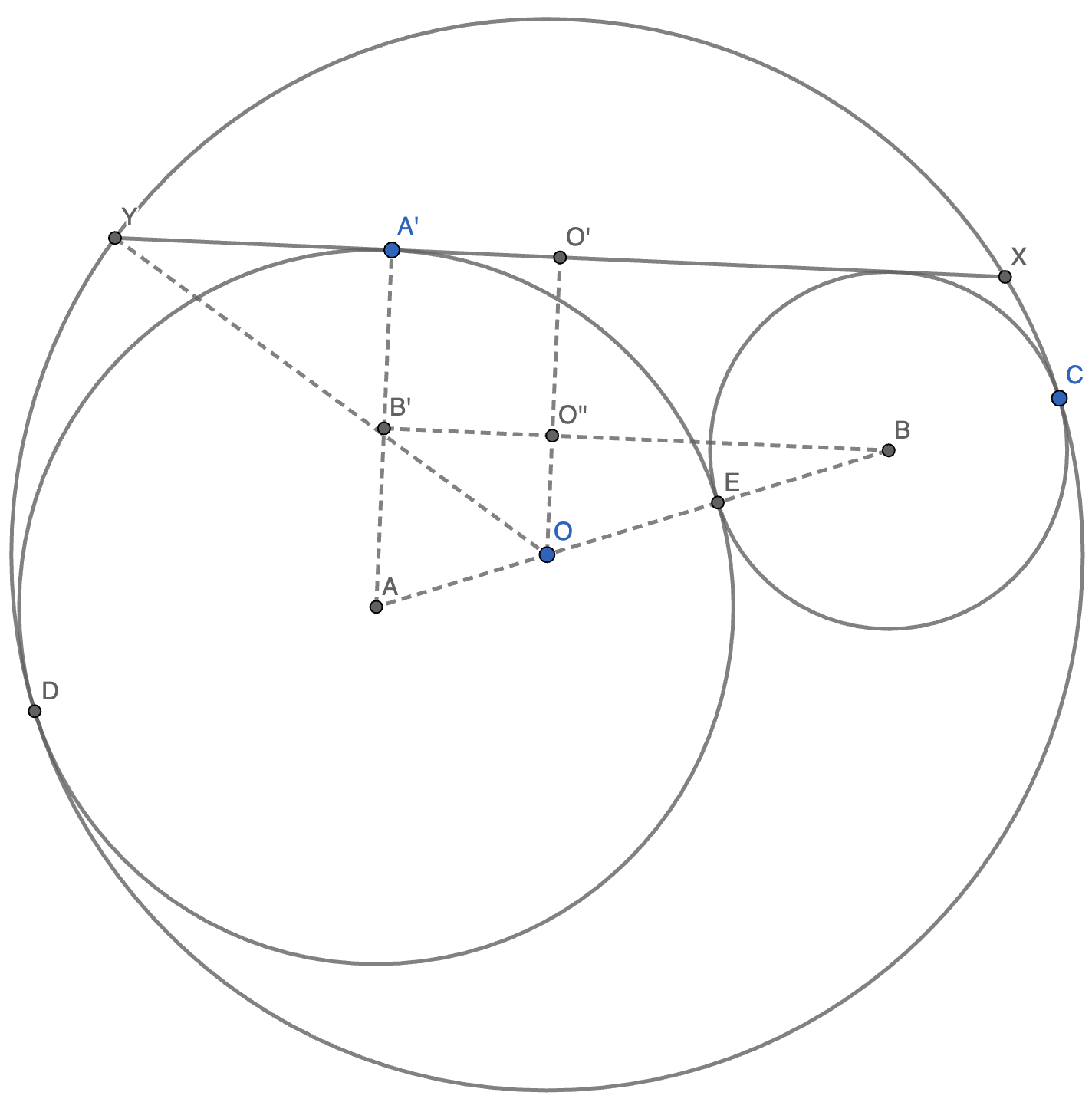
5.（1995 AIME 第 4 题）已知：

• \(\odot O\) 的半径为 \(9\)，\(\odot A\) 的半径为 \(6\)，\(\odot B\) 的半径为 \(3\)。
• \(\odot A\) 与 \(\odot B\) 相切。
• \(\odot A, \odot B\) 都与 \(\odot O\) 内切。
• \(\odot O\) 上的弦 \(XY\) 与 \(\odot A, \odot B\) 同时相切，其中点 \(Y\) 更靠近 \(\odot A\)。

求 \(XY^2\) 的值。

正解：

作 \(AA' \perp XY\) 于 \(A'\)，\(OO' \perp XY\) 于 \(O'\)，\(BB' \perp AA'\) 于 \(B'\)。设 \(OO'\) 交 \(BB'\) 于 \(O''\)。

容易发现，\(AB' = A'B' = O'O'' = AO = EO = BE = 3\)，且 \(\triangle BOO' \sim \triangle BAB'\)，且相似比为 \(BO : AB = 2 : 3\)。故 \(OO'' = 2 \implies OO' = OO'' + O'O'' = 5\)。

又知 \(OY = 9\)，故 \(O'Y^2 = OY^2 - OO'^2 = 9^2 - 5^2 = 56 \implies XY^2 = (2O'Y)^2 = 4O'Y^2 = 224\)。

6. 已知 \(a + b = \pi / 12\)，求 \(\dfrac{1 - \tan(a) - \tan(b) - \tan(a) \tan(b)}{1 + \tan(a) + \tan(b) - \tan(a) \tan(b)}\) 的值。

正解：令 \(\tan(a + b) = \dfrac{\tan(a) + \tan(b)}{1 - \tan(a) \tan(b)} = \dfrac{p}{q}\)，则原式为 \(\dfrac{q - p}{q + p} = \dfrac{1 - p / q}{1 + p / q}\)。

易知 \(\dfrac{p}{q} = \tan(\pi / 12) = 2 - \sqrt{3}\)，则原式为 \(\dfrac{\sqrt{3} - 1}{3 - \sqrt{3}} = \dfrac{\sqrt{3}}{3}\)。

函数篇

1. 函数 \(f(x) = x^2 - 4\) 关于原点逆时针旋转了 \(60 \degree\) 得 \(g(x)\)，求出 \(f\) 和 \(g\) 在第四象限的交点。

正解：设 \(f\) 和 \(g\) 共同组成图形 \(\omega\)，则 \(f\) 和 \(g\) 的交点一定在 \(\omega\) 的对称轴上。

因为旋转了 \(60 \degree\)，所以对称轴与 \(y\) 轴的夹角为 \(30 \degree\)。因为关于原点旋转，所以对称轴过原点。

则 \(y = -\sqrt{3} x\)，此时只需求出 \(y = -\sqrt{3} x\) 与 \(f\) 在第四象限的交点即可。

将两式联立，解得 \(x = \dfrac{-\sqrt{3} \pm \sqrt{19}}{2}\)，则所求交点为 \(\left( \dfrac{-\sqrt{3} + \sqrt{19}}{2}, \dfrac{3 - \sqrt{57}}{2} \right)\)。

2. 求函数 \(f(x) = \sqrt{x^2 - 2x + 2} + \sqrt{x^2 - 4x + 8}\) 的最小值。

正解：配方得 \(f(x) = \sqrt{(x - 1)^2 + 1} + \sqrt{(x - 2)^2 + 4}\)。

设 \(A(1, 1), B(2, -2), X(x, 0)\)，则 \(f(x) = AX + BX\)。（技巧：见到根号里是平方和，就要想到两点距离公式。）

想要 \(f(x)\) 取到最小值，那么 \(X\) 在 \(AB\) 上，则 \(x = \dfrac{4}{3}, \min(f(x)) = f \left( \dfrac{4}{3} \right) = \sqrt{10}\)。

数论篇

1. 求证：不存在连续 \(18\) 个正整数，满足它们各恰有 \(2\) 个质因子。

证明：因为有连续 \(18\) 个正整数，故必有 \(\dfrac{18}{6} = 3\) 个 \(6\) 的倍数。设它们为 \(6n, 6(n + 1), 6(n + 2)\)。

因为这些正整数各恰有 \(2\) 个质因子，而 \(6\) 已经有 \(2\) 个质因子（\(2\) 与 \(3\)），故 \(n, n + 1, n + 2\) 都只能有 \(2, 3\) 这两个质因子。

满足条件的只有 \(n = 1\) 与 \(n = 2\) 两种情况，检验可发现它们都不满足条件，故不存在满足给定条件的构造。证毕。

2. 设 \(m \perp n\)，求证：\(\dfrac{(m + n - 1)!}{m! \cdot n!} \in \mathbb{Z}\)。

证明：注意到，\(\dfrac{(m + n - 1)!}{m! \cdot n!} = \dfrac{1}{m + n} \dbinom{m + n}{m}\) 为 \(m\) 个红球与 \(n\) 个蓝球作圆排列的方案数，故其一定为整数。

3. 证明：存在连续的 \(666\) 个正整数，其中恰有 \(66\) 个质数。

证明： \(f(x)\) 表示 \([x, x + 665]\) 中质数个数。容易发现，\(|f(x) - f(x + 1)| = 1\)。

又因为 \([667! + 2, 667! + 667]\) 中没有质数，所以 \(f(667! + 2) = 0\)。

同时，\(f(1) > 66\)，故 \(\{ f(1), f(1) - 1, \cdots, 67, 66, 65, \cdots, 1, 0 \} \sube \{ f(1), f(2), \cdots, f(667! + 1), f(667! + 2) \}\)，故 \(\exist x \in [1, 667! + 2] \cap \N_+, f(x) = 66\)。

4. 设 \(x_1, x_2, \cdots, x_{2014}\) 模 \(2014\) 互不同余，\(y_1, y_2, \cdots, y_{2014}\) 模 \(2014\) 也互不同余。证明：不存在 \(y\) 的排列 \(z\) 满足 \(x_1 + z_1, x_2 + z_2, \cdots, x_{2014} + z_{2014}\) 模 \(2014\) 互不同余。

证明：假设存在。

容易发现，\(\sum \limits_{i = 1}^{2014} x_i \equiv \sum \limits_{i = 1}^{2014} y_i \equiv \sum \limits_{i = 1}^{2014} x_i + y_i \equiv 1007 \pmod{2014}\)

但是 \(\sum \limits_{i = 1}^{2014} x_i + y_i \equiv \sum \limits_{i = 1}^{2014} x_i + \sum \limits_{i = 1}^{2014} y_i \equiv 0 \pmod{2014}\)，矛盾！

故不存在。

5. 证明：任意正整数 \(n\) 都可以表示成 \(a - b\) 的形式，满足 \(a, b\) 不同质因子的数量相同。

证明：

• 若 \(2 \mid n\)：令 \(a = 2n, b = n\)。

  证明：设 \(n = 2^k m\)，则 \(2n = 2^{k + 1} m\)，与 \(n\) 的质因子数量相同。

• 否则：令 \(p\) 为最小不整除 \(n\) 的奇质数，令 \(a = pn, b = (p - 1)n\)。

  证明：设 \(n\) 的质因子集合为 \(\mathbb{P}_n\)，则 \(\mathbb{P}_{p - 1} \sube \mathbb{P}_n \cup \{ 2 \}\)，故 \(pn, (p - 1)n\) 都只在 \(n\) 的基础上多了质因子 \(2\)，故质因子数量相同。

6. 求证：对于任意 \(n \ge 2\)，都有 \(\sum \limits_{i = 2}^n \lfloor \sqrt[i]{n} \rfloor = \sum \limits_{i = 2}^n \lfloor \log_i(n) \rfloor\)。

证明：

给两边都 \(+n\)，则只需证 \(n + \lfloor \sqrt{n} \rfloor + \lfloor \sqrt[3]{n} \rfloor + \cdots + \lfloor \sqrt[n]{n} \rfloor = n + \lfloor \log_2 n \rfloor + \lfloor \log_3 n \rfloor + \cdots + \lfloor \log_n n \rfloor\)。

注意到：

\[\begin{aligned} \mathrm{LHS} &= \sum_{i = 1}^n \sum_{j = 1}^n [j^i \le n] \\ \mathrm{RHS} &= \sum \limits_{i = 1}^n \sum \limits_{j = 1}^n [i^j \le n] \\ &= \sum \limits_{j = 1}^n \sum \limits_{i = 1}^n [i^j \le n] \\ &= \sum \limits_{i = 1}^n \sum \limits_{j = 1}^n [j^i \le n] \\ &= \mathrm{LHS} \end{aligned} \]

其中：

\[[\mathrm{P}] = \begin{cases} 1, &\text{P is true} \\ 0, &\text{otherwise} \end{cases} \]

组合数学篇

1. 已知 \(A \cup B \cup C = \{ 1, 2, 3, \ldots, 10 \}\)，求满足条件的有序三元组 \((A, B, C)\) 的个数。

正解：给每个元素寻找归属，每个元素可以属于 \(A\)、\(B\)、\(C\)、\(A\) 和 \(B\)、\(A\) 和 \(C\)、\(B\) 和 \(C\)、\(A\) 和 \(B\) 和 \(C\)，共 \(7\) 种可能。

故答案为 \(7^{10}\)。

2. 已知集合 \(A\) 满足：

• \(A \sube \{ 1, 2, \cdots, 100 \}\)。
• 若 \(x \in A\)，则 \(2x \notin A\)。

求 \(\max(|A|)\)。

正解：建无向图 \(G\)，把 \(x\) 和 \(2x\) 连边，则答案为 \(G\) 中最大独立集的大小。

注意到 \(G\) 是由一条条链组成的，所以只需对每条链求最大独立集大小，然后再加起来。

长度为 \(l\) 的链的最大独立集大小为 \(\lceil l / 2 \rceil\)。

下附代码，输出为 \(67\)。

#include <iostream>
#include <vector>

using namespace std;

constexpr int N = 100;

vector<vector<int>> G(N + 1);
vector<bool> vis(N + 1);

int size(int u)
{
    int res = 1;
    vis[u] = true;

    for (int v : G[u]) {
        if (!vis[v])
            res += size(v);
    }

    return res;
}

int main()
{
    for (int i = 1; i <= N / 2; ++i) {
        G[i].emplace_back(i * 2);
        G[i * 2].emplace_back(i);
    }

    int ans = 0;

    for (int i = 1; i <= N; ++i) {
        if (!vis[i])
            ans += (size(i) + 1) / 2;
    }

    cout << ans << '\n';
    return 0;
}

3. 集合 \(A\) 满足：

• \(A \subsetneq \{ 1, 2, 3, \ldots, 8 \}\)。
• \(\sum \limits_{x \in A} x^2\) 是奇数。

求 \(A\) 的个数。

解法 1（生成函数）：设：

\[f(x) = \prod \limits_{i = 1}^8 \left( 1 + x^{i^2} \right) \]

则 \([x^n] f(x)\) 为 \(\sum \limits_{x \in A} x^2 = n\) 的 \(A\) 的个数，则我们要求：

\[\sum \limits_{2 \nmid i} [x^i] f(x) \]

我们考虑代入特殊值可以发现：

\[\begin{aligned} \sum \limits_{2 \nmid i} [x^i] f(x) &= \dfrac{f(1) - f(-1)}{2} \\ &= \dfrac{2^8 - 0}{2} \\ &= 2^7 \end{aligned} \]

解法 2：我们只关心模 \(2\) 意义下的值，则构造 \(A\) 相当于选 \(x \le 4\) 个 \(0\)、\(y \le 4\) 个 \(1\) 满足 \(2 \nmid y\)。方案数为：

\[\begin{aligned} \sum_{i = 0}^4 \sum_{\substack{2 \nmid j \\ j \le 4}} \dbinom{4}{i} \dbinom{4}{j} &= \left( \sum_{i = 0}^4 \dbinom{4}{i} \right) \left( \sum_{\substack{2 \nmid j \\ j \le 4}} \dbinom{4}{j} \right) \\ &= 2^4 \cdot 2^3 \\ &= 2^7 \end{aligned} \]

神秘题目

1. 定义数列 \(f\)：

\[\begin{cases} f_1 = 1 \\ f_{2n} = f_n \\ f_{2n + 1} = f_n + 1 \end{cases} \]

求 \(\max \limits_{i = 1}^{2022} f_i\)。

正解：设 \(f_n\) 是第 \(n\) 个数，则有递推式：

\[\begin{cases} f_1 = 1 \\ f_{2n} = f_n \\ f_{2n + 1} = f_n + 1 \end{cases} \]

注意到 \(f_n\) 恰好是 \(n\) 的二进制表示中的 \(1\) 的个数，则答案为 \([1, 2022]\) 中二进制表示中 \(1\) 的个数的最大值。

最大值在 \(n = (10111111111)_2\) 时取到，为 \(10\)。

2. 对于一个正整数 \(n\)，若其满足以下条件，则称其为“金猴数”：

• \(n\) 可以被分解为若干个正整数相加。
• 这些正整数的倒数和为 \(1\)。

解决以下问题：

2.1. 证明：\(11\) 和 \(28\) 是两个“金猴数”。

正解：因为 \(11 = 2 + 3 + 6\)，且 \(1/2 + 1/3 + 1/6 = 1\)，所以 \(11\) 是“金猴数”。因为 \(28 = 8 + 8 + 4 + 4 + 4\)，且 \(1/8 + 1/8 + 1/4 + 1/4 + 1/4 = 1\)，所以 \(11\) 是“金猴数”。

2.2. 证明：若 \(n\) 是“金猴数”，则 \(2n + 2\) 与 \(2n + 9\) 均为“金猴数”。

正解：设 \(n = \sum \limits_j a_j\)，则 \(\sum \limits_j \dfrac{1}{a_j} = 1\)，则 \(\sum \limits_j \dfrac{1}{2a_j} = 1/2\)，则 \(1/2 + \sum \limits_j \dfrac{1}{2a_j} = 1\)。又发现 \(2n + 2 = 2 + \sum \limits_j 2a_j\)，且 \(1/2 + \sum \limits_j \dfrac{1}{2a_j} = 1\)，所以 \(2n + 2\) 是“金猴数”。

又发现 \(1/3 + 1/6 + \sum \limits_j \dfrac{1}{2a_j} = 1\)，则 \(2n + 9 = 3 + 6 + \sum \limits_j 2a_j\)，且 \(1/3 + 1/6 + \sum \limits_j \dfrac{1}{2a_j} = 1\)，所以 \(2n + 9\) 是“金猴数”。

2.3. 证明：\(2023\) 是“金猴数”。

正解：

• 因为 \(28\) 是“金猴数”，
• 所以 \(28 \times 2 + 2 = 58\) 是“金猴数”，
• 所以 \(58 \times 2 + 2 = 118\) 是“金猴数”，
• 所以 \(118 \times 2 + 9 = 245\) 是“金猴数”。
• 所以 \(245 \times 2 + 9 = 499\) 是“金猴数”。
• 所以 \(499 \times 2 + 9 = 1007\) 是“金猴数”。
• 所以 \(1007 \times 2 + 9 = 2023\) 是“金猴数”。