模拟赛题补

[Round 6] 最小值

Description

给定两个长度为 \(N(N\leq 2\times 10^5)\) 的正整数序列 \(A\) 和 \(B\)，对于每个 \(k \in [1,n]\)，求在所有长度为 \(k\) 的区间 \([l,r]\) 中，\(\big \lvert\min\limits_{i=l}^r\{A_i\}-\min\limits_{i=l}^r\{B_i\}\rvert\) 的最小值。

Solution

分治。

对于一个分治区间 \([l,r]\)，\(mid=\lfloor \dfrac{l+r}{2}\rfloor\)，令：

\(C_i=\min\limits_{i=l}^{mid}\{A_i\},D_i=\min\limits_{i=l}^{mid}\{B_i\},E_i=\min\limits_{i=mid+1}^{r}\{A_i\},F_i=\min\limits_{i=mid+1}^{r}\{B_i\}\)

那么对于一个横跨 \(mid\) 的区间 \([L,R]\)：

\(\lvert\min\limits_{i=L}^R\{A_i\}-\min\limits_{i=L}^R\{B_i\}\rvert = \lvert \min(C_L,E_R)-\min(D_L,F_R)\rvert\)

分类讨论：

1. \(C_L \leq E_R,D_L \leq F_R\)，原式 $ = \lvert C_L-D_L\rvert$
2. \(C_L > E_R,D_L > F_R\)，原式 $ = \lvert E_R-F_R\rvert$
3. \(C_L \leq E_R,D_L > F_R\)，原式 $ = \lvert C_L-F_R\rvert$
4. \(C_L > E_R,D_L \leq F_R\)，原式 $ = \lvert D_L-E_R\rvert$

我们枚举长度 \(k\)，所以 \(R=L+k-1\)。

因为 \(C\) 递增，\(E\) 递减，二分出最后一个 \(C_i \leq E_{i+k-1}\) 的位置，记为 \(P\)。
同理，\(D\) 递增，\(F\) 递减，二分出最后一个 \(D_i \leq F_{i+k-1}\) 的位置，记为 \(Q\)。

所以四种情况：

1. \(L \leq P\) 且 \(L \leq Q\)，预处理最小值。
2. \(L > P\) 且 \(L > Q\)，同上。
3. \(Q < L \leq P\)，二分出最后一个 \(C_i \leq F_{i+k-1}\) 的位置（即交点），此时绝对值最小。
4. \(P < L \leq Q\)，同上。

时间复杂度 \(\mathcal O(N\log^2N)\)。

注意：本题实现细节较多。

点击查看代码

#include<bits/stdc++.h>
#define FASTIO ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define rep(i,l,r) for(int i=(l); i<=(r); ++i)
#define drep(i,r,l) for(int i=(r); i>=(l); --i)
using namespace std;
const int N=2e5+5,INF=2e9;
int n,a[N],b[N],c[N],d[N],lg[N],ans[N];
struct ST {
	int A[20][N];
	inline void init(int n) {
		rep(j,1,19) rep(i,1,n-(1<<j)+1)
		A[j][i]=min(A[j-1][i],A[j-1][i+(1<<j-1)]);
	}
	inline int qry(int l,int r) {
		int k=lg[r-l+1];
		return min(A[k][l],A[k][r-(1<<k)+1]);
	}
} A,B,F,G;
inline void sol(int l,int r) {
#define C(i) A.qry(i,mid)
#define D(i) B.qry(i,mid)
#define E(i) A.qry(mid+1,i)
#define F(i) B.qry(mid+1,i)
	if(l==r) return;
	int mid=(l+r)>>1;
	sol(l,mid),sol(mid+1,r);
	rep(i,l,mid) F.A[0][i-l+1]=abs(C(i)-D(i));
	rep(i,mid+1,r) G.A[0][i-mid]=abs(E(i)-F(i));
	F.init(mid-l+1),G.init(r-mid);
	rep(k,2,r-l+1) {
		int sl=max(l,mid-k+2),sr=min(mid,r-k+1);
		int P,Q,L=sl,R=sr,M;
		while(L<R) M=(L+R+1)>>1,C(M)<=E(M+k-1)?L=M:R=M-1;
		if(C(L)>E(L+k-1)) --L;
		P=L,L=sl-1,R=sr;
		while(L<R) M=(L+R+1)>>1,D(M)<=F(M+k-1)?L=M:R=M-1;
		if(D(L)>F(L+k-1)) --L;
		Q=L;
		ans[k]=min(ans[k],min(min(P,Q)>=sl?F.qry(sl-l+1,min(P,Q)-l+1):INF,max(P,Q)<=sr-1?G.qry(max(P,Q)+k-mid,sr+k-1-mid):INF));
		L=max(sl,Q+1)-1,R=min(sr,P);
		while(L<R) M=(L+R+1)>>1,C(M)<=F(M+k-1)?L=M:R=M-1;
		ans[k]=min(ans[k],min(L>=max(sl,Q+1)?abs(C(L)-F(L+k-1)):INF,L<min(sr,P)?abs(C(L+1)-F(L+k)):INF));
		L=max(sl,P+1)-1,R=min(sr,Q);
		while(L<R) M=(L+R+1)>>1,D(M)<=E(M+k-1)?L=M:R=M-1;
		ans[k]=min(ans[k],min(L>=max(sl,P+1)?abs(D(L)-E(L+k-1)):INF,L<min(sr,Q)?abs(D(L+1)-E(L+k)):INF));
	}
}
signed main() {
	FASTIO;
	memset(ans,0x3f,sizeof ans);
	cin>>n,lg[1]=0;
	rep(i,2,n) lg[i]=lg[i>>1]+1;
	rep(i,1,n) cin>>a[i],A.A[0][i]=a[i];
	rep(i,1,n) cin>>b[i],B.A[0][i]=b[i],ans[1]=min(ans[1],abs(a[i]-b[i]));
	A.init(n),B.init(n);
	sol(1,n);
	rep(i,1,n) cout<<ans[i]<<'\n';
}

[Round 7] number

Description

初始有一个仅由 \(2\) 和 \(7\) 构成的数字串，可以对其进行以下三种操作任意次，问能得到多少种长度 \(\leq m(m \leq 10^{18})\) 的数字串。

• 在任意位置插入子串 \(222\)，或删除一个子串 \(222\)。
• 在任意位置插入子串 \(77\)，或删除一个子串 \(77\)。
• 在任意位置插入子串 \(2727\)，或删除一个子串 \(2727\)。

Solution

妙。

要将数字串 \(S\) 变为 \(T\)，那么可以将 \(S\) 先变为 \(K\) 再变为 \(T\)。

其中 \(K\) 是 \(S\) 和 \(T\) 能变为的长度最小的串。

发现 \(K\) 只有 \(6\) 种可能，分别为 \(\empty,2,7,22,27,72\)。

这 \(6\) 种最小串构成如下图的变化方式：

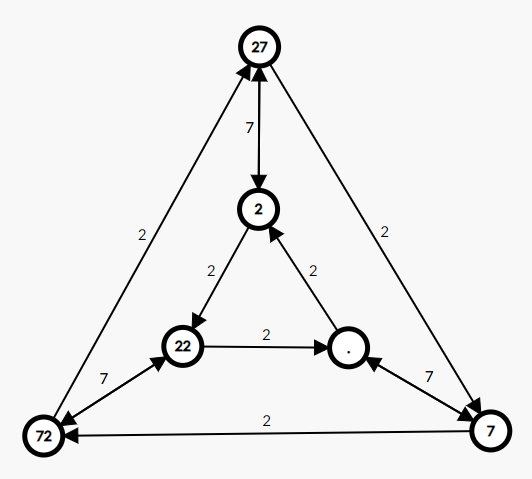
变化过程

$\empty+2=2\\$ $\empty+7=7\\$ $2+2=22\\$ $2+7=27\\$ $7+2=72\\$ $7+7=77-77=\empty\\$ $22+2=222-222=\empty\\$ $22+7=227+2727=2227277-222=7277-77=72\\$ $27+7=277-77=2\\$ $27+2=272+77=27277-2727=7\\$ $72+2=722+2727=7222727-222=7727-77=27\\$ $72+7=727+222=222727-2727=22\\$

因此可以设 \(f_{i,j}\) 表示长度为 \(i\)，能变为的最小串的种类为 \(j\) 的不同数字串数量。

若最小串 \(i\) 到最小串 \(j\) 有边，记 \(A_{i,j}=1\)。

\(f_{0,0}=1,f_{i,j}=\sum\limits_{A_{k,j}}{f_{i-1,k}}\)

观察发现是矩阵快速幂的形式，因为所有 \(len \leq m\) 的串都要算在答案里面，最终答案即：

\(\sum\limits_{i=0}^m{A^i}=\dfrac{A^{m+1}-1}{A-1}\)

需要使用矩阵求逆，不易求。

记 \(\mathcal S(n)=\sum\limits_{i=0}^n{A^i}\)，那么 \(\mathcal S(2n)=\mathcal S(n)\times(A^n+1)\)。

于是可以用倍增求解，时间复杂度 \(\mathcal O(6^3\times\log m)\)。

点击查看代码

#include<bits/stdc++.h>
#define FASTIO ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define rep(i,l,r) for(int i=(l); i<=(r); ++i)
#define drep(i,r,l) for(int i=(r); i>=(l); --i)
using namespace std;
const int N=5e6+5,P=998244353;
int _,m,K,T[6][2];
string s;
struct Matrix {
	int a[6][6];
	Matrix() {memset(a,0,sizeof a);}
	inline Matrix operator+(const Matrix&b) {Matrix c;rep(i,0,5) rep(j,0,5) c.a[i][j]=(a[i][j]+b.a[i][j])%P;return c;}
	inline Matrix operator*(const Matrix&b) {Matrix c;rep(i,0,5) rep(j,0,5) rep(k,0,5) (c.a[i][j]+=a[i][k]*b.a[k][j]%P)%=P;return c;}
} A,F[65],S[65];
inline int calc(int K,int m) {
	int p=log2(m),now=1ll<<p;
	Matrix R=S[p],C=F[p];
	drep(i,p,0) if(now+(1ll<<i)<=m) R=R+C*S[i],C=C*F[i],now+=(1ll<<i);
	return R.a[0][K];
}
inline void sol() {
	cin>>s>>m,K=0;
	for(auto c:s) K=T[K][c=='7'];
	cout<<calc(K,m)+(!K)<<'\n';
}
signed main() {
	FASTIO;
	T[0][0]=1,T[1][0]=3,T[2][0]=4,T[4][0]=5,T[5][0]=2;
	T[0][1]=2,T[1][1]=5,T[3][1]=4,T[4][1]=3,T[5][1]=1;
	rep(i,0,5) rep(j,0,1) ++A.a[i][T[i][j]];
	F[0]=S[0]=A;
	rep(i,1,60) F[i]=F[i-1]*F[i-1],S[i]=S[i-1]+S[i-1]*F[i-1];
	cin>>_;
	while(_--) sol();
}