「HDU5072」Coprime

Description

从元素个数为 \(n(n \leq 10^5)\) 的给定数集 \(a(a_i \leq 10^5)\) 中选择三个元素使得这三个数两两互质或两两不互质，求选择这样三个数的方案数。

Solution

将互质的两个数之间连上蓝边，不互质的两个数连上红边，如图：

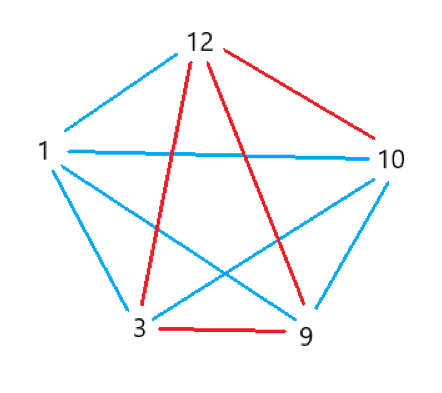
于是任务变为了求同色三元环的的个数，可以通过求异色三元环的个数得到。

上图中异色角的个数一共有 \(4+4+3+3=14\) 个，总方案数为 \(\binom{5}{3}=10\)，答案 \(3\) 恰好等于 \(10-\dfrac{14}{2}\)。

发现统计异色角的个数恰好统计了 \(2\) 次，因为异色三元环必定刚好有一对异色角。

那么问题转化为与 \(i\) 相连的蓝边的个数 \(k_i\) 即：

\[k_i = \sum_{j}{[\gcd(a_i,a_j)=1]} \]

所以与 \(i\) 相连的异色角的个数就是 \(k_i*(n-k_i-1)\)（红蓝边相匹配）。

这个东西可以用容斥解决，考虑求不互质的数的个数。

记 \(c_i\) 为 \(a\) 中是 \(i\) 的倍数的数的个数，与 \(a_i\) 不互质的数的个数就是：

\[\sum_{d|i}{c_d*\mu(d)} \]

带入计算即可，时间复杂度 \(\mathcal O(n \sqrt n)\)。

qwq，不会用线性筛，只能用埃氏筛了...

点击查看代码

#include<bits/stdc++.h>
#define FASTIO ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define int long long
#define rep(i,l,r) for(int i=(l); i<=(r); ++i)
#define drep(i,r,l) for(int i=(r); i>=(l); --i)
using namespace std;
const int N=1e5+5;
int _,n,a[N],c[N];
int u[N],v[N];
vector<int>fac[N];
inline void init(int n) {
	fill(u+1,u+n+1,-1);
	rep(i,2,n) if(!v[i]) {
		u[i]=1;
		rep(j,2,n/i) v[i*j]=1,u[i*j]=-u[i*j];
		rep(j,1,n/(i*i)) u[i*i*j]=0;
	}
	rep(i,2,n) rep(j,1,n/i) fac[i*j].push_back(i);
}
signed main() {
	FASTIO;
	cin>>_,init(N-5);
	while(_--) {
		memset(c,0,sizeof c);
		int sum=0;
		cin>>n;
		rep(i,1,n) {
			cin>>a[i];
			for(auto x:fac[a[i]]) ++c[x];
		}
		rep(i,1,n) {
			if(a[i]==1) continue;
			int cnt=0;
			for(auto x:fac[a[i]]) cnt+=c[x]*u[x];
			--cnt,sum+=(n-cnt-1)*cnt;
		}
		cout<<n*(n-1)*(n-2)/6-sum/2<<'\n';
	}
}