平移变换深入理解

文章通过对关于平移变换讨论，涵盖几何平移、代数平移及数据预处理中的平移操作，结合数学本质、应用场景与核心差异进行系统梳理：

---

一、平移变换的数学本质与分类

1. 几何平移

• 定义：在几何空间中，将点、向量或图形沿指定方向移动固定距离，保持形状、大小、方向不变。

• 数学形式：

  • 二维：点 𝑃(𝑥,𝑦) 平移向量 𝑣=(𝑎,𝑏) 后坐标为：

    

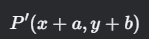
  • 齐次坐标矩阵表示（便于复合变换）：

    

     

    ​​

• 核心性质：

  • 等距性：保持距离、角度、面积不变。

  • 无不动点（非零平移）。

  • 可逆性：逆变换为反向平移向量 −𝑣。

2. 代数平移

• 定义：通过加减常数对数值或数据集进行整体位移，调整其范围或基线。

• 数学形式：

  • 数据平移：𝑋′=𝑋−𝑋_min（将数据对齐到零点）。

  • 参数方程：随时间 𝑡t 的匀速平移（如 ）。

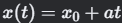• 核心性质：

  • 分布不变性：保持数据相对差值和比例。

  • 可逆性：通过反向加减恢复原始数据。

---

二、几何平移与数据平移的对比

维度	几何平移	数据平移
操作对象	点、向量、几何图形	数值序列、数据集、信号
数学形式	向量加法或齐次坐标矩阵乘法	标量加减（如 𝑋′=𝑋−𝑐）
核心目的	改变空间位置，保持几何结构	调整数据基线，消除偏移或标准化范围
不变性	距离、角度、面积	相对差值、分布形态（方差、偏度等）
典型应用	图形学、机器人运动学、坐标系变换	数据归一化、信号处理、特征工程
依赖参数	平移向量（人为指定或动态计算）	统计量（如 𝑋min​、均值）

---

三、平移操作的核心意义

1. 共同特征

• 结构保持性：几何平移保持图形全等，数据平移保持分布形态。

• 可逆性：通过反向操作恢复原始状态。

• 线性操作：几何平移在齐次坐标下为线性矩阵运算，数据平移为仿射变换特例。

2. 数学本质

• 仿射变换的子集：平移是“线性变换 + 平移”中的基础操作。

• 群论视角：所有平移构成阿贝尔群（满足封闭性、结合律、存在单位元和逆元）。

---

四、应用场景与限制

1. 几何平移

• 应用：

  • 计算机图形学（物体移动、视角变换）。

  • 物理学（刚体平动描述）。

  • 地图绘制（坐标系转换）。

• 限制：

  • 需明确平移向量，不适用于非刚性变形场景。

2. 数据平移

• 应用：

  • 数据标准化：Min-Max归一化的前置步骤（𝑋′=𝑋−𝑋_min）。

  • 信号处理：消除传感器基线漂移（如ECG信号校正）。

  • 图像处理：调整像素值范围（如 [50,200]→[0,150]）。

• 限制：

  • 异常值敏感：若 𝑋_min为离群点，导致范围失真。

  • 掩盖负值分布：对含负值的数据可能破坏原始对称性（如金融收益率）。

---

五、操作公式与示例

1. 几何平移示例

• 二维平移矩阵：

  

   

  ​​

  作用于点 (1,1)得到 (4,−1)。

2. 数据平移示例

• 原始数据：[5,10,15]，𝑋_min=5
  

• 平移后：[0,5,10]
  

• 新范围：[0,10]
  

---

六、总结与选择建议

场景	推荐平移类型	关键理由
图形移动或坐标系对齐	几何平移	保持空间关系，支持复合变换（旋转+平移）
数据归一化或基线校正	数据平移（𝑋−𝑐）	消除偏移，适配后续算法（如神经网络输入）
含负值或对称分布数据	避免平移，改用Z-score	保留分布对称性，避免误导性范围调整

---

通过以上梳理，可系统理解平移在不同领域的数学统一性与应用差异性，为理论分析与实践操作提供清晰指导。