数据平移是什么

数据预处理中的平移操作（例如 𝑋′=𝑋−𝑋_min）属于代数平移的一种形式，但与几何平移的数学意义和应用场景存在差异。以下从数学定义、核心性质、与几何平移的对比等方面进行详细分析：

---

1. 代数平移的数学定义

在数据科学或统计学中，平移操作通过加减常数对数据进行整体位移，其一般形式为：

𝑋′=𝑋+𝑐或𝑋′=𝑋−𝑐

其中 c 为常数（如 𝑋_min​、均值等）。比如公式 𝑋′=𝑋−𝑋_min​ 是典型的平移操作，将数据范围对齐到以0为起点的位置。

数学本质

• 仿射变换的特例：平移是仿射变换（线性变换 + 平移）的简化形式，仅包含平移项，无线性变换部分。

• 保持线性关系：平移后数据的相对差值和比例不变，即：

  

  因此，数据的分布形态（如方差、协方差）不受影响。

---

2. 与几何平移的对比

虽然几何平移和数据平移都涉及“位移”，但目标、应用场景和数学意义有所不同：

维度	几何平移	数据平移（如 𝑋′=𝑋−𝑋min​)
操作对象	点、向量、几何图形（空间位置）	数据集（数值序列、特征值）
数学形式	𝑃′=𝑃+𝑣（向量加法）	𝑋′=𝑋−𝑐（标量运算）
核心目的	改变位置，保持几何结构不变	调整数据分布范围，消除基线偏移
不变性	保持距离、角度、面积等度量性质	保持数据相对关系（如差值、分布形态）
典型应用	图形学中的物体移动、坐标系变换	数据归一化、特征工程、信号处理
限制条件	平移向量需人为指定	平移量依赖数据统计量（如 𝑋min)

---

3. 数据平移的核心作用

(1) 消除负值与基线偏移

• 示例：传感器采集的原始数据存在基线偏移（如 𝑋_min=1000），通过平移 𝑋′=𝑋−1000，可将有效信号范围对齐到0附近，便于后续分析。

• 适用场景：图像处理（像素值平移）、生物信号处理（ECG/EEG基线校正）。

(2) 数据范围标准化

• 归一化前处理：在Min-Max归一化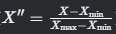（）中，平移操作是第一步，将数据映射到 [0,1] 的基础步骤。

• 示例：原始数据 [5,15]→ 平移后 [0,10] → 归一化后 [0,1]。

(3) 保留分布形态

平移操作不改变数据的统计特性（如方差、偏度、峰度），仅调整位置参数（如均值、中位数）。

---

4. 数据平移的局限性

(1) 对负值数据的处理风险

• 问题：若数据包含负值（如金融收益率 [−5%,10%]），平移 𝑋′=𝑋−(−5%) 后范围变为 [0,15%]，可能掩盖原始分布的对称性。

• 解决方案：需结合业务意义判断是否适用平移，或改用其他标准化方法（如Z-score标准化）。

(2) 异常值敏感

• 问题：若 𝑋_min​ 是异常值（如数据主体为 [0,10]，但 𝑋_min=−100），平移后范围变为 [100,110]，导致数值分布失真。

• 解决方案：使用稳健统计量（如中位数）替代 𝑋_min​，或提前清洗异常值。

---

5. 数学意义总结

数据平移 𝑋′=𝑋−𝑐 的数学本质是仿射变换的特例，其意义体现在：

1. 线性运算的简化：平移是线性空间中的加法操作，属于线性变换的子集。

2. 分布不变性：保持数据的内在结构（如差异、比例），仅调整全局位置。

3. 应用普适性：适用于任何数值型数据，是数据预处理的基石操作。

---

6. 与几何平移的共性

尽管应用场景不同，两者在以下层面具有一致性：

• 操作形式：通过加减常数实现整体位移。

• 不变性原理：保持“结构”不变（几何形状/数据分布）。

• 可逆性：平移操作可通过反向加减恢复原始数据或位置。

---

示例深化理解

场景1：图像像素值平移

• 原始数据：某图像像素范围 [50,200]（因光照偏暗）。

• 平移操作：𝑋′=𝑋−50，新范围 [0,150]。

• 意义：便于后续对比度增强或归一化到 [0,1]。

场景2：温度数据校正

• 原始数据：传感器因误差记录为 [−5°𝐶,25°𝐶]（实际应为 [0°𝐶,30°𝐶]）。

• 平移操作：𝑋′=𝑋+5，校正后 [0°𝐶,30°𝐶]。

• 意义：消除设备基线误差，还原真实物理量。

---

结论

您提到的数据平移 𝑋′=𝑋−𝑋_min​ 是代数平移的重要应用，其数学意义与几何平移一脉相承，均通过加减操作实现整体位移并保持结构不变性。它在数据科学中扮演了“位置校准”的角色，是特征工程和信号处理的基础工具，但需结合实际数据分布和业务需求谨慎使用。