斜率优化
斜率优化dp
我之前写的怎么是一坨啊
对于 dp 转移式子类似于 \(f_i=\min(f_j+val(i,j))\) 的形式,其中 \(val(i,j)\) 中含有 \(i\times j\) 的项。
对于 \(\max\) 也同理。
特别地,如果 \(val(i,j)\) 中不含与 \(i\times j\) 有关的项,可以用普通的单调队列优化,这里不再赘述。
看不懂没关系,看例题。
例题
设 \(f_i\) 表示考虑到第 \(i\) 个玩具时的最小费用。
方程:
我们设 \(sum_i=\sum_{j=1}^i c_j\),即前缀和,\(l=L+1\)。化简式子:
设 \(s_i=sum_i+i\)。
以下为了简便,我们只考虑 \(\min\) 内的式子。
拆掉平方。
我们考虑在什么情况下,对于 \(j_1<j_2<i\),\(j_2\) 优于 \(j_1\)。
当且仅当满足 \(f_{j_1}+(s_{j_1}+l)^2-2s_i s_{j_1}\ge f_{j_2}+(s_{j_2}+l)^2-2s_i s_{j_2}\)。
此时化简重点思路:用含 \(j_1\) 和 \(j_2\) 的式子表示与 \(i\) 有关的式子。
在这里,我们设 \(a_i=(s_i+l)^2\),\(y_i=f_i+a_i\),\(x_i=s_i\)。
式子就转化为了:
此时这个式子就是个斜率的公式。
所以一个决策点 \(j\),可以看作平面上 \(x=s_j\),\(y=f_j+a_j\) 的点。
所以定义斜率 \(slope(j_1,j_2)=\frac{y_{j_2}-y_{j_1}}{x_{j_2}-x_{j_1}}\)。
如果两点间连线的斜率 \(slope(j_1,j_2)\le 2s_i\),那么 \(j_1\) 就可以走人了,因为 \(j_2\) 比它优。
注意(我踩过的坑):只有两个决策点是不可以确定谁优的,必须要根据不同的 \(i\) 决定。
我们考虑有没有什么情况是可以排除点的。
考虑对于三个点 \(i,j,k\),满足如下关系:
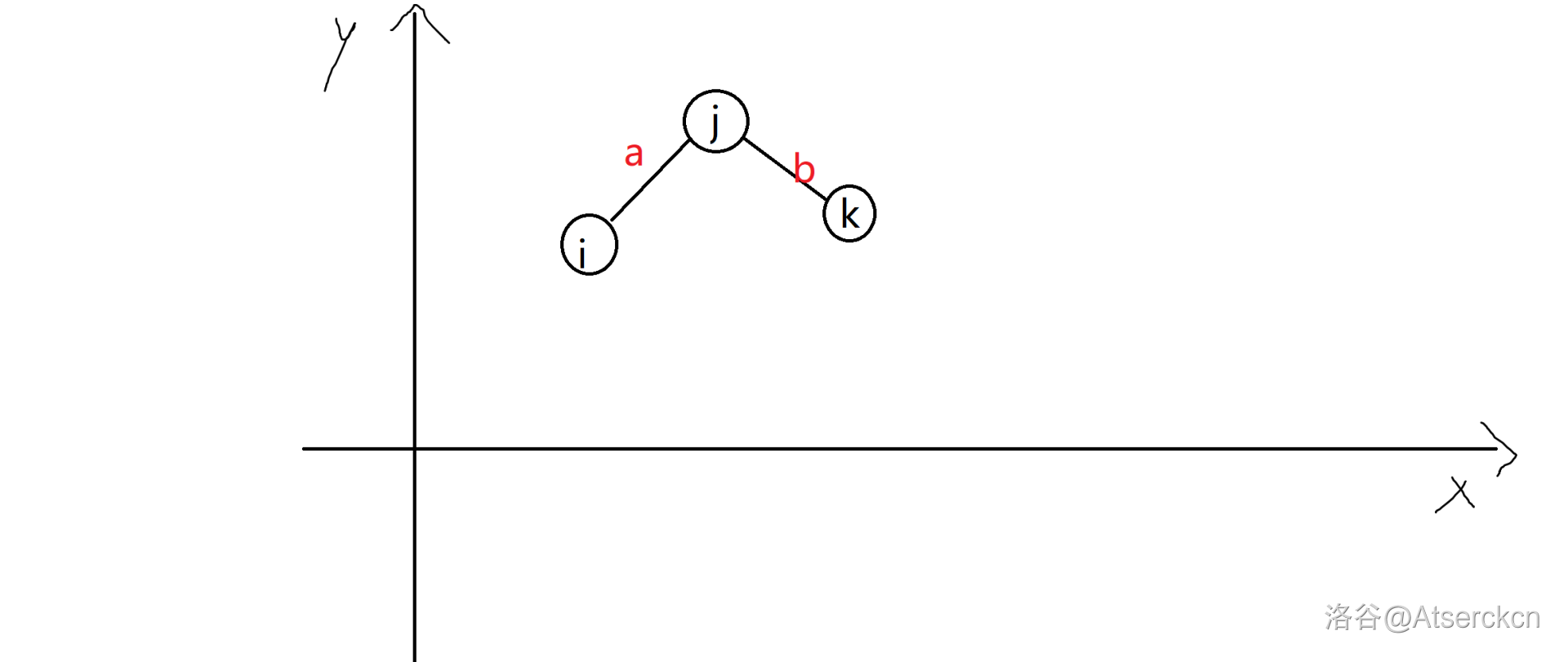
其中,\(slope(i,j)=a,slope(j,k)=b,a\ge b\)。
我们注意到点 \(j\)。
如果 \(j\) 是最优决策,根据上文所述,必然有:
- 和 \(i\) 比:\(a\le 2s_i\)。
- 和 \(k\) 比:\(b>2s_i\)。
那么就与 \(a\ge b\) 矛盾了,所以 \(j\) 在三者中肯定不是最优决策。
所以 \(j\) 就可以滚蛋了。
其实单调队列的本质就是在加入元素前想办法删除队头,加入元素时想办法删除队尾,最后加入新元素。
那么删除队头的判断是哪个呢?就是淘汰掉 \(j_1\) 的式子 \(slope(j_1,j_2)\le 2s_i\)。
那么删除中间的 \(j\) 该怎么搞呢?
我们把新元素当作 \(k\),队尾是 \(j\),队尾的前一个是 \(i\)。
如果满足条件 \(slope(i,j)\ge slope(j,k)\) 的话,就可以弹出队尾。
最后给个代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ljl;
inline void Rd(auto &num);
const int N=5e4+5;
const ljl inf=1e18;
ljl n,l,c[N],s[N],f[N];
int dq[N],h=1,t=0;
ljl a(int i){return s[i]*s[i]+2*s[i]*l;}
ljl b(int i){return (s[i]-l)*(s[i]-l);}
double y(int j){return (double)f[j]+(double)a(j);}
double x(int j){return (double)s[j];}
double slope(int j1,int j2){return (y(j2)-y(j1))/(x(j2)-x(j1));}
int main(){
Rd(n);Rd(l);++l;
for(int i=1;i<=n;++i){
Rd(c[i]);s[i]=s[i-1]+c[i];f[i]=inf;}
for(int i=1;i<=n;++i)s[i]+=i;
dq[++t]=0;
for(int i=1;i<=n;++i)
{
while(h<t&&slope(dq[h],dq[h+1])<=(double)2.0*s[i])
++h;
int j=dq[h];
f[i]=f[j]+a(j)-2*s[i]*s[j]+b(i);
while(h<t&&slope(dq[t-1],dq[t])>slope(dq[t],i))
--t;
dq[++t]=i;
}
printf("%lld\n",f[n]);
return 0;
}
inline void Rd(auto &num)
{
num=0;char ch=getchar();bool f=0;
while(ch<'0'||ch>'9')
{
if(ch=='-')f=1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
num=(num<<1)+(num<<3)+(ch-'0');
ch=getchar();
}
if(f)num=-num;
return;
}
FZYZ 寒假集训,花了大半天的时间学的东西。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号