浅谈可持久化数据结构
浅谈可持久化数据结构
可持久化
可持久化意思是支持查询历史任意时间的状态和数据。
本文以可持久化线段树(主席树)和可持久化字典树(Trie)举例。
(其实是其他我也没学)
写在前面的技巧
本文主要的东西叫做“版本”或“历史时间”,在主席树例题一中它是修改的时间,但是在大多数题目中,他是加入元素的时间。
比如依次加入序列 1 5 4 3 2
那么在加入 \(4\) 时,有贡献的时间区间是 \([1,2]\)。
再比如类似于前缀和的思想。
要查询区间 \([t_1,t_2]\),可以转化为 \([1,t_2]-[1,t_1-1]\)。
比如查询一个区间 \([t_1,t_2]\) 的信息,就可以是用维护 \([1,t_2]\) 的数据结构在信息中减去维护 \([1,t_1-1]\) 的数据结构所得的结果。
有点绕,不过绕就对了。(这可是我研究一周的结果)
可持久化线段树
可持久化线段树又称为主席树。
因为发明者的名字首字母是 hjt,是当时主席。
给个问题:
如果你要维护一个数列,支持若干次修改操作,查询历史上任意时刻的某一位置的值,如何操作?
暴力的方式是对于每次操作,都开个线段树存信息。
但这样显然时间空间都爆炸。
注意到一次修改,由于线段树的特性,每次修改只会影响 \(\log n\) 个节点。
所以大部分的节点是与上一代线段树一样的,可以建个根节点 \(rt\),有重复的节点直接连边过去。
这里就用到了类似动态开点线段树的性质。
最后可以确保对于任意的 \(rt\),把它为根的子树拎出来,得到的是一棵完整的树。
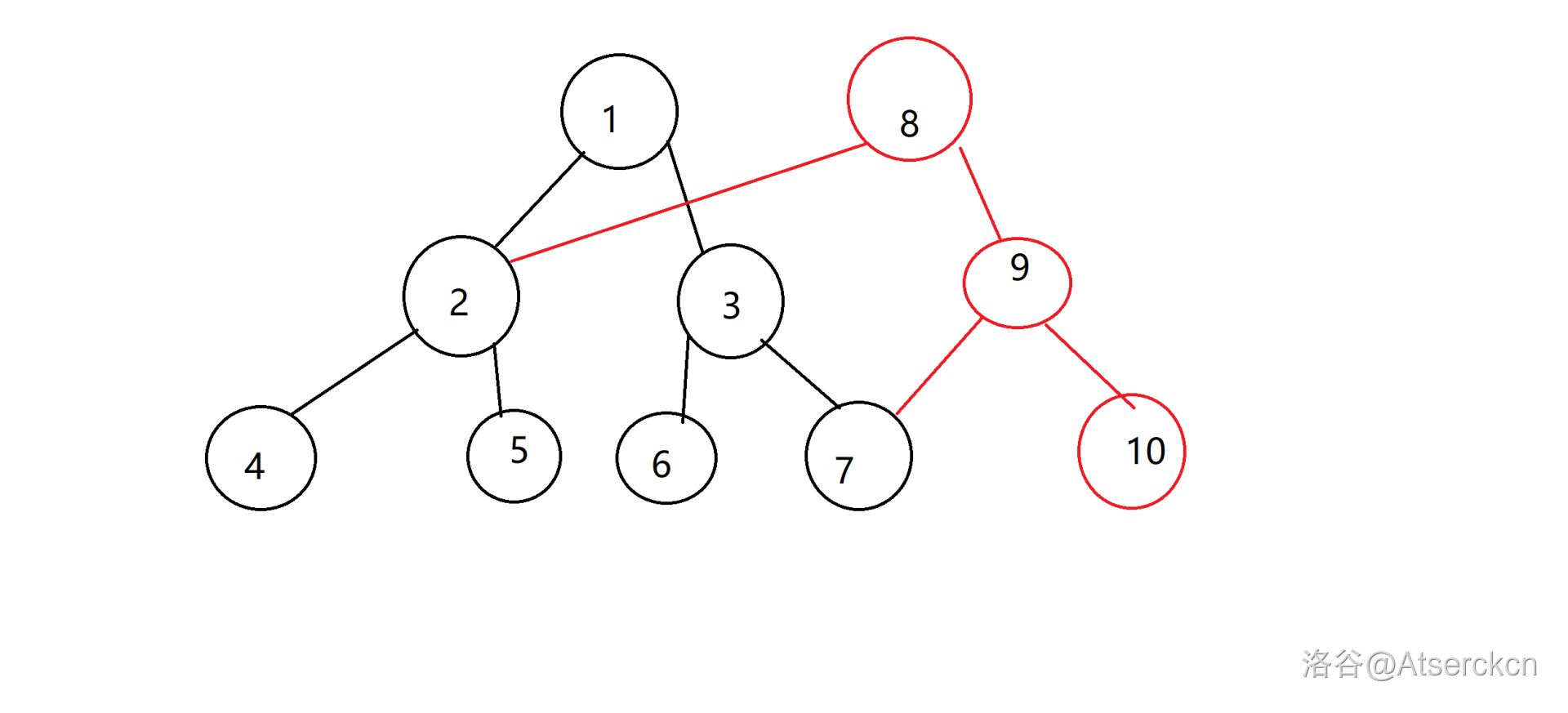
例如上图。
黑色的线段树是上个历史时刻的信息,而如果我们只改了最右边的节点,一大堆节点(以 \(2\) 为根的子树和点 \(7\))是不变的,所以这边直接连边过去。
这样存的信息是什么?
是前缀区间 \([1,q]\) 的所有历史信息。
对于几乎所有的可持久化数据结构,插入和查询都是要有一个现节点和一个上节点一起跳。方便维护和复制信息。
所以例题:
洛谷 P3919 【模板】可持久化线段树 1(可持久化数组)
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ljl;
#define FUP(i,x,y) for(auto (i)=(x);(i)<=(y);++(i))
#define FDW(i,x,y) for(auto (i)=(x);(i)>=(y);--(i))
inline void Rd(auto &num);
const int N=1e6+5;
int n,m,a[N];
namespace SMT{
struct NODE{
int l,r,lc,rc,sum;
}node[N*40];
int tot,rt[N];
int newnode(int l,int r){node[++tot].l=l;node[tot].r=r;return tot;}
void pushup(int p)
{
if(node[p].l==node[p].r)return;
node[p].sum=node[node[p].lc].sum+node[node[p].rc].sum;
return;
}
void bld(int l,int r,int &p)
{
if(!p)p=newnode(l,r);
node[p].l=l;node[p].r=r;
if(l==r){node[p].sum=a[l];return;}
int mid=(node[p].l+node[p].r)>>1;
bld(l,mid,node[p].lc);bld(mid+1,r,node[p].rc);
pushup(p);
return;
}
void upd(int &p,int lst,int pos,int val)
{
p=newnode(node[lst].l,node[lst].r);
node[p]=node[lst];
if(node[p].l==node[p].r){node[p].sum=val;return;}
int mid=(node[p].l+node[p].r)>>1;
if(pos<=mid)
upd(node[p].lc,node[lst].lc,pos,val);
else
upd(node[p].rc,node[lst].rc,pos,val);
pushup(p);
return;
}
int query(int p,int pos)
{
if(node[p].l==node[p].r&&node[p].l==pos)return node[p].sum;
int mid=(node[p].l+node[p].r)>>1;
if(pos<=mid)return query(node[p].lc,pos);
else return query(node[p].rc,pos);
}
}
using namespace SMT;
int main(){
Rd(n);Rd(m);
FUP(i,1,n)Rd(a[i]);
bld(1,n,rt[0]);int v,op,p,c;
FUP(i,1,m)
{
Rd(v);Rd(op);
if(op&1)
{
Rd(p);Rd(c);
upd(rt[i],rt[v],p,c);
}
else
{
Rd(p);
printf("%d\n",query(rt[v],p));
rt[i]=rt[v];
}
}
return 0;
}
inline void Rd(auto &num)
{
num=0;char ch=getchar();bool f=0;
while(ch<'0'||ch>'9')
{
if(ch=='-')f=1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
num=(num<<1)+(num<<3)+(ch-'0');
ch=getchar();
}
if(f)num=-num;
return;
}
然后我们可以再深点,看看下面的典题:静态区间第 \(k\) 小。
这题是个值域主席树,因为 \(a_i\) 的值太大了,所以要用离散化。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ljl;
#define FUP(i,x,y) for(auto (i)=(x);(i)<=(y);++(i))
#define FDW(i,x,y) for(auto (i)=(x);(i)>=(y);--(i))
inline void Rd(auto &num);
const int N=2e5+5;
int n,m,a[N],rt[N],maxn,b[N];
void sol()
{
FUP(i,1,n)b[i]=a[i];
sort(b+1,b+n+1);
int c=unique(b+1,b+n+1)-b-1;maxn=c;
FUP(i,1,n)
a[i]=lower_bound(b+1,b+c+1,a[i])-b;
// FUP(i,1,n)cout<<a[i]<<' ';
// cout<<'\n';
return;
}
namespace SMT{
int tot;
struct NODE{
int lc,rc,l,r,sum;
}node[N*40];
int newnode(int l,int r)
{
node[++tot].l=l;node[tot].r=r;
return tot;
}
void pushup(int p)
{
if(node[p].l==node[p].r)return;
node[p].sum=node[node[p].lc].sum+node[node[p].rc].sum;return;
}
void bld(int l,int r,int &p)
{
p=newnode(l,r);
if(l==r){node[p].sum=0;return;}
int mid=(l+r)>>1;
bld(l,mid,node[p].lc);bld(mid+1,r,node[p].rc);
pushup(p);
return;
}
void upd(int &p,int lst,int pos,int val)
{
p=++tot;
node[p]=node[lst];
if(node[p].l==node[p].r&&node[p].l==pos){node[p].sum+=val;return;}
int mid=(node[p].l+node[p].r)>>1;
if(pos<=mid)upd(node[p].lc,node[lst].lc,pos,val);
else upd(node[p].rc,node[lst].rc,pos,val);
pushup(p);
return;
}
int query(int p,int lst,int k)//重点在这里
{
if(node[p].l==node[p].r)return node[p].l;
int lsum=node[node[p].lc].sum-node[node[lst].lc].sum;//左子树的有lsum个数
// int rsum=node[node[p].rc].sum-node[node[lst].rc].sum;
if(k<=lsum)return query(node[p].lc,node[lst].lc,k);//往左子树找
else return query(node[p].rc,node[lst].rc,k-lsum);//否则往右子树找
}
}
using namespace SMT;
int main(){
Rd(n);Rd(m);
FUP(i,1,n)Rd(a[i]);
sol();bld(1,maxn,rt[0]);
FUP(i,1,n)
upd(rt[i],rt[i-1],a[i],1);
int l,r,k;
while(m--)
{
Rd(l);Rd(r);Rd(k);
printf("%d\n",b[query(rt[r],rt[l-1],k)]);
}
return 0;
}
inline void Rd(auto &num)
{
num=0;char ch=getchar();bool f=0;
while(ch<'0'||ch>'9')
{
if(ch=='-')f=1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
num=(num<<1)+(num<<3)+(ch-'0');
ch=getchar();
}
if(f)num=-num;
return;
}
可持久化字典树(Trie)
具体示意图跟主席树挺像的,不放图了。
不过大部分可持久化 Trie 不是真让你存字符信息,而是和异或绑一起考,参考洛谷 P10471 最大异或对 The XOR Largest Pair。也欢迎来看我滴题解~(link,洛谷题解区里也有)。
闲话:不说我都忘了好多题解都没放进我的 blog 里面,这篇就是现场 copy 过去的。
如果不知道怎么用字典树求最大异或值的建议先看我的那篇题解。
给例题:洛谷 P4735 最大异或和
首先推推式子,再前缀异或和一下,发现是求区间 \([l−1,r−1]\) 中异或 \(s_n\oplus x\) 的最大值。
上文的技巧部分说了,可以用 \(r-1\) 版本的字典树减去 \(l-1\) 版本的字典树,再参考最大异或和的方法贪心跑,就能得到答案。注意特判 \(l-1\) 别越界了。
#include<bits/stdc++.h>
using namespace std;
typedef long long ljl;
#define FUP(i,x,y) for(auto (i)=(x);(i)<=(y);++(i))
#define FDW(i,x,y) for(auto (i)=(x);(i)>=(y);--(i))
inline void Rd(auto &num);
const int N=6e5+5;
int n,m,a[N],s[N];
namespace TRIE{
int tot,rt[N],cntrt;
struct NODE{
int son[2],lst;
}node[N*35];
void Insert(int x,int cur,int lst)
{
for(int i=30;i>=0;--i)
{
node[cur].lst=node[lst].lst+1;
int o=((x>>i)&1);
if(!node[cur].son[o])node[cur].son[o]=++tot;
node[cur].son[!o]=node[lst].son[!o];
cur=node[cur].son[o];lst=node[lst].son[o];
}
node[cur].lst=node[lst].lst+1;
return;
}
int query(int cur,int lst,int val)
{
int ans=0;
for(int i=30;i>=0;--i)
{
int o=((val>>i)&1);
if(node[node[cur].son[!o]].lst-node[node[lst].son[!o]].lst>0)
{
ans+=(1<<i);
cur=node[cur].son[!o];
lst=node[lst].son[!o];
}
else cur=node[cur].son[o],lst=node[lst].son[o];
}
return ans;
}
}
using namespace TRIE;
void getch(char &ch)
{
ch=getchar();
while(ch!='A'&&ch!='Q')ch=getchar();
return;
}
int main(){
Rd(n);Rd(m);cntrt=n;
FUP(i,1,n){
Rd(a[i]);s[i]=s[i-1]^a[i];}
FUP(i,1,n)
{
rt[i]=++tot;
Insert(s[i],rt[i],rt[i-1]);
}
char ch;int l,r,x;
while(m--)
{
getch(ch);
if(ch=='A')
{
Rd(x);
rt[++cntrt]=++tot;s[cntrt]=s[cntrt-1]^x;
Insert(s[cntrt],rt[cntrt],rt[cntrt-1]);
}
else
{
Rd(l);Rd(r);Rd(x);--l;--r;
if(!l)
printf("%d\n",max(s[cntrt]^x,query(rt[r],rt[0],s[cntrt]^x)));
else
printf("%d\n",query(rt[r],rt[l-1],s[cntrt]^x));
}
}
return 0;
}
inline void Rd(auto &num)
{
num=0;char ch=getchar();bool f=0;
while(ch<'0'||ch>'9')
{
if(ch=='-')f=1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
num=(num<<1)+(num<<3)+(ch-'0');
ch=getchar();
}
if(f)num=-num;
return;
}
还有恶心点的例题:
FZYZ 校内集训推的题。
为了写它,花了一周时间学可持久化数据结构,终于在今天写出来这题了/kk
主要是题解区讲解都不是很详细。
首先树上差分的思想,查询点 \(x,y\) 的路径可以转化为 \([1,x]+[1,y]-[1,lca]-[1,fa_{lca}]\)。
对于第一种询问,直接把树拍成 dfs 序,记为 \(dfn_x\),维护子树大小,以 \(x\) 为根的子树所映射成的区间是 \([dfn_x,dfn_x+siz_x-1]\)。这个直接可持久化 Trie 搞搞即可。
对于第二个询问则要用上文差分的思想,不过不是 dfs 序,就是原编号。
所以维护两个 Trie,一个是以 dfs 序建树,另一个是在 dfs 时,儿子的版本由父亲的版本更新。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ljl;
#define FUP(i,x,y) for(auto (i)=(x);(i)<=(y);++(i))
#define FDW(i,x,y) for(auto (i)=(x);(i)>=(y);--(i))
inline void Rd(auto &num);
const int N=1e5+5;
int q,n,cnt_e,ehead[N],a[N],tot,fa[N][25],dep[N],dfn[N];
int rt[N*2],rk[N],siz[N];
struct E{
int to,pre;
}e[N<<1];
void adde(int from,int to)
{
e[++cnt_e].to=to;
e[cnt_e].pre=ehead[from];
ehead[from]=cnt_e;
return;
}
struct NODE{
int son[2],cnt;
}node[N*32*2];
void Insert(int cur,int lst,int x)
{
for(int i=30;i>=0;--i)
{
node[cur].cnt=node[lst].cnt+1;
int o=((x>>i)&1);
if(!node[cur].son[o])node[cur].son[o]=++tot;
node[cur].son[!o]=node[lst].son[!o];
cur=node[cur].son[o];lst=node[lst].son[o];
}
node[cur].cnt=node[lst].cnt+1;
return;
}
int Q1(int x,int cur,int lst)
{
int ans=0;
for(int i=30;i>=0;--i)
{
int o=((x>>i)&1);
if(node[node[cur].son[!o]].cnt-node[node[lst].son[!o]].cnt>0)
{
ans+=(1<<i);
cur=node[cur].son[!o];lst=node[lst].son[!o];
}
else
cur=node[cur].son[o],lst=node[lst].son[o];
}
return ans;
}
int Q2(int x,int rt1,int rt2,int l1,int l2)
{
int ans=0;
FDW(i,30,0)
{
int o=((x>>i)&1);
if(node[node[rt1].son[!o]].cnt+node[node[rt2].son[!o]].cnt-
node[node[l1].son[!o]].cnt-node[node[l2].son[!o]].cnt>0)
{
ans+=(1<<i);
rt1=node[rt1].son[!o];rt2=node[rt2].son[!o];
l1=node[l1].son[!o];l2=node[l2].son[!o];
}
else
{
rt1=node[rt1].son[o];rt2=node[rt2].son[o];
l1=node[l1].son[o];l2=node[l2].son[o];
}
}
return ans;
}
int query1(int l,int r,int x){return Q1(x,rt[r],rt[l-1]);}
void dfs(int u,int uf)
{
fa[u][0]=uf;dep[u]=dep[uf]+1;siz[u]=1;
dfn[u]=++dfn[0];rk[dfn[0]]=u;
FUP(i,1,20)fa[u][i]=fa[fa[u][i-1]][i-1];
rt[N+u]=++tot;Insert(rt[N+u],rt[N+uf],a[u]);
for(int i=ehead[u];i;i=e[i].pre)
{
int v=e[i].to;
if(v==uf)continue;
dfs(v,u);siz[u]+=siz[v];
}
return;
}
int getlca(int u,int v)
{
if(dep[u]<dep[v])swap(u,v);
FDW(i,20,0)
if(dep[u]-(1<<i)>=dep[v])u=fa[u][i];
if(u==v)return u;
FDW(i,20,0)
if(fa[u][i]!=fa[v][i])
u=fa[u][i],v=fa[v][i];
return fa[u][0];
}
int query2(int x,int y,int lca,int flca,int val){return Q2(val,rt[N+x],rt[N+y],rt[N+lca],rt[N+flca]);}
int main(){
Rd(n);Rd(q);
FUP(i,1,n)Rd(a[i]);
for(int i=1,u,v;i<n;++i)
{
Rd(u);Rd(v);
adde(u,v);adde(v,u);
}
dfs(1,0);int op,x,y,z;
FUP(i,1,n)
Insert(rt[i]=++tot,rt[i-1],a[rk[i]]);
while(q--)
{
Rd(op);
if(op&1)
{
Rd(x);Rd(z);
printf("%d\n",query1(dfn[x],dfn[x]+siz[x]-1,z));
}
else
{
Rd(x),Rd(y),Rd(z);
int lca=getlca(x,y),flca=fa[lca][0];
printf("%d\n",query2(x,y,lca,flca,z));
}
}
return 0;
}
inline void Rd(auto &num)
{
num=0;char ch=getchar();bool f=0;
while(ch<'0'||ch>'9')
{
if(ch=='-')f=1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
num=(num<<1)+(num<<3)+(ch-'0');
ch=getchar();
}
if(f)num=-num;
return;
}
完结撒花,下班,也祝我生日快乐。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号