二维偏序（离线二维数点）

二维偏序（离线二维数点）

问题

在 \([l,r]\) 的区间内，有多少个数 \(\le x\)。共 \(m\) 次询问。

暴力：\(O(nm)\) 的 check。效率低下。

离线二维数点

可以将询问离线下来。

首先运用下差分的思想，将 \(ans[l,r]\) 分解为 \(ans[1,r]-ans[1,l-1]\)。

所以考虑按照端点从小到大排序，转化为 \(2m\) 个询问。

对于某个询问 \((r,x,id,opt)\)：

• \(r\) 表示询问区间是 \([1,r]\)。
• \(x\) 表示多少个数 \(\le x\)。
• \(id\) 因为是离线，所以需要询问编号。
• \(opt\) 是该询问的系数。比如 \([1,r]\) 的系数是 \(1\)，\([1,l-1]\) 则为 \(-1\)。

所以可以将一个询问看成一个点 \((r,x)\)。在平面直角坐标系中，将 \(r\) 看成横坐标，\(x\) 看成 \(y\) 坐标。

那么问题又转化为了对于一个点 \(A(x_a,y_a)\)，有多少个点 \(B(x_b,y_b)\) 满足 \(x_a\ge x_b\and y_a\ge y_b\)。
画成图就是这样：

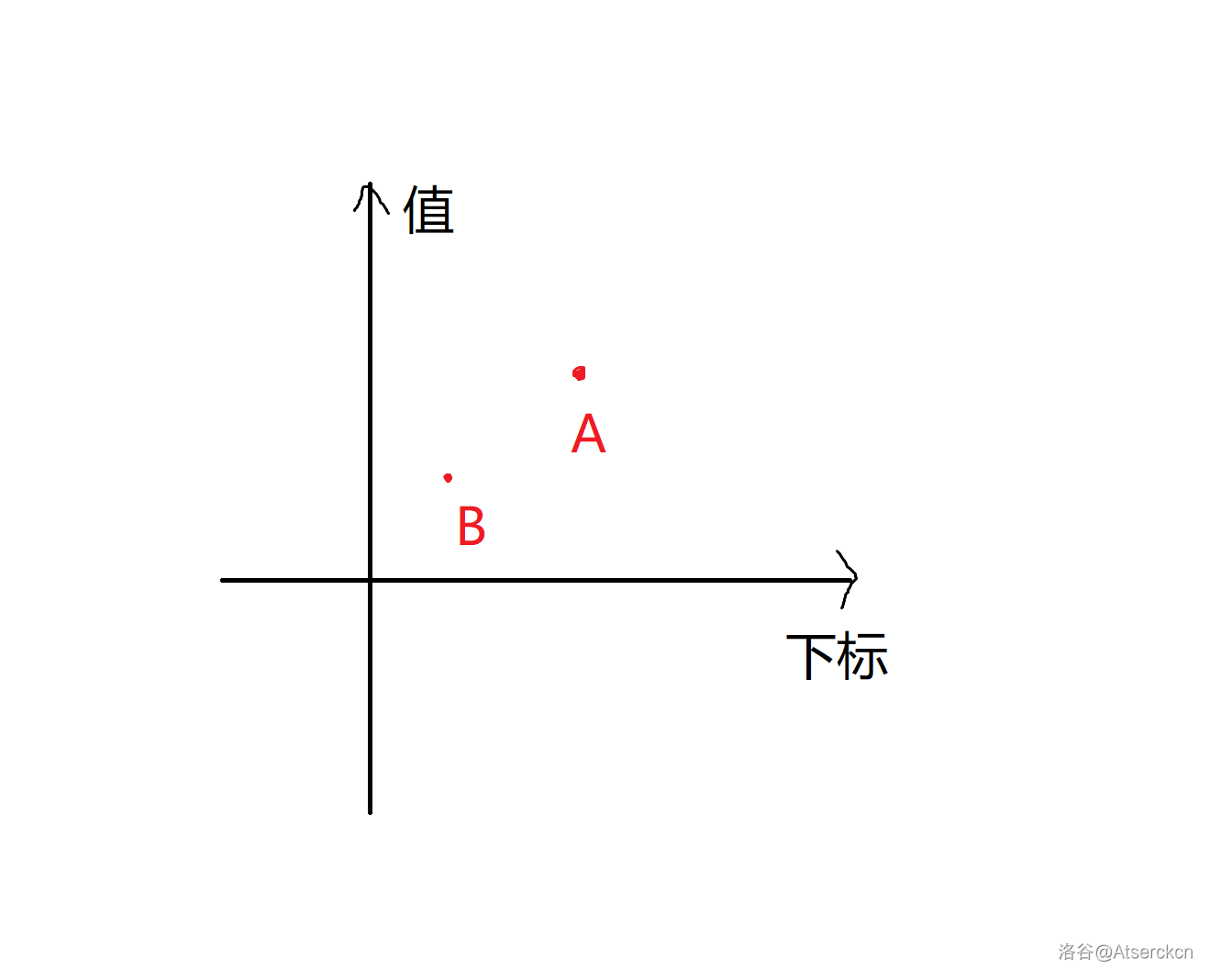
所以就可以解释为什么要按照端点下标从小到大排序。

最后我们维护一个可区间操作的数据结构，比如说线段树或树状数组维护 \(y\) 坐标。

如果值很大就离散化一下。

例题

洛谷 P10814 【模板】离线二维数点。

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ljl;
#define FUP(i,x,y) for(int i=(x);i<=(y);++i)
#define FDW(i,x,y) for(int i=(x);i>=(y);--i)
inline void Rd(auto &num);
const int N=2e6+5;
int n,m,a[N],tc[N],cntn,ans[N];
struct NODE{
	int r,x,Id,op;
	bool operator < (const NODE &oth)const{
		if(r!=oth.r)return r<oth.r;
		return x<oth.x;
	}
}node[N*2];//注意要开2m的空间
//树状数组 begin
int lowbit(int x){return x&(-x);}
void addc(int x)
{
	for(;x<N;x+=lowbit(x))++tc[x];
	return;
}
int ask(int x)
{
	int ans=0;
	for(;x;x-=lowbit(x))ans+=tc[x];
	return ans;
}
//树状数组 end
int main(){
	Rd(n);Rd(m);
	FUP(i,1,n)Rd(a[i]);
	FUP(i,1,m)
	{
		int l,r,x;Rd(l);Rd(r);Rd(x);
        //拆分为两个询问
		node[++cntn].r=r;node[cntn].x=x;node[cntn].Id=i;node[cntn].op=1;
		node[++cntn].r=l-1;node[cntn].x=x;node[cntn].Id=i;node[cntn].op=-1;
	}
	sort(node+1,node+cntn+1);
	int j=1;
	FUP(i,1,cntn)
	{
		int u=node[i].r,I=node[i].Id,x=node[i].x,op=node[i].op;
		while(j<=u)addc(a[j++]);//这里对于所有下标<=u的元素都加进来
		ans[I]+=ask(x)*op;
	}
	FUP(i,1,m)
		printf("%d\n",ans[i]);
	return 0;
}
inline void Rd(auto &num)
{
	num=0;char ch=getchar();bool f=0;
	while(ch<'0'||ch>'9')
	{
		if(ch=='-')f=1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		num=(num<<1)+(num<<3)+(ch-'0');
		ch=getchar();
	}
	if(f)num=-num;
	return;
}